The Story of Thorn
- Transfer

Spike everywhere
We call him “Spikey” [Spikey], and in my life today I meet him constantly:

He comes from a three-dimensional object, a polyhedron called “rhombic six-sided”.

But what is its story and why did we make it our symbol?
Origin of thorny
In 1987, when we were developing the first version of Mathematica, one of its innovations was the ability to generate independent of the resolution of three-dimensional graphics based on symbolic descriptions. In early demonstrations, this allowed us to produce surprisingly clear images of regular polyhedra. But, coming closer to the release of Mathematica 1.0, we wanted to use some more impressive example. Therefore, we decided to take the last regular polyhedron — the icosahedron — and make something more complicated from it by giving it a star-like shape, or, more correctly, cumulation. Yes, this is exactly what the first interface of the notebook looked like 30 years ago.

At first it was just a pretty demonstration that quickly worked on our computers at that time. But soon the three-dimensional object generated by it became de facto used as a logo for Mathematica. And by the time version 1.0 was released in 1988, the star-shaped icosahedron was everywhere:

Over time, various initiations to our star-shaped polyhedron began to appear - made in different materials and sizes:

But just a year after the release of Mathematica 1.0, we were ready to release Mathematica 1.2, and that to convey the complexity of the product, we needed a complicated logo. One of our developers, Igor Rivin, defended his doctorate on the topic of polyhedra in hyperbolic space - and thanks to his efforts our materials for version 1.2 decorated the hyperbolic icosahedron:

My employees gave me a T-shirt with then-modern Shipastic for my 30th birthday in 1989, and a quote that I support even after so many years:

“Company is fun”
After the release of Mathematica 1.2, we could find a whole collection of hyperbolic in our marketing materials. regular polyhedra, but with the advent of version 2.0 in 1991, we decided that we liked the hyperbolic icosahedron most of all:

But we continued to explore other spiny forms. Inspired by Leonardo da Vinci's drawing of a “wooden model” of a starry icosahedron (made with surprisingly accurate observation of perspective) for the book by Luca Pacioli“On Divine Proportion,” we ordered a poster of version 2.0, where five intersecting tetrahedrons are arranged so that their outer peaks form the dodecahedron:

Today, looking through my archives from 1991, I find the “explanatory” code, and it's nice to see that it is easily executed in our latest version of the Wolfram Language (although today it can be written a little more elegantly):

Over the years, this has become a strange ritual - preparing for the launch of the next major version of Mathematica, we will organize serious meetings where we are “choosing the new Thorny.” Sometimes you have to choose from hundreds of different options created using completely different algorithms:

But, although the color palettes are modified, and Spike often reflect the presence of new features in the system (albeit somewhat latently), we have a 30-year tradition of choosing options for a hyperbolic dodecahedron:

Recently, it has become common to study parametric space - although now we have already accumulated hundreds of parameters :
The hyperbolic dodecahedron has 20 vertices - this is ideal for celebrating the 20th anniversary of Mathematica in 2008. But when we wanted to do something similar for the 25th anniversary in 2013, we were faced with the problem of the absence of regular polyhedra with 25 vertices. But (as a matter of fact, using the SpherePoints function [25]), we were able to create an approximate figure , and printed it on a 3D printer for all company employees, with dimensions corresponding to the length of service of employees.

Wolfram | Alpha Exit
In 2009, we were preparing to release Wolfram | Alpha, and the system needed a logo. There were many concepts:

We would like to emphasize that Wolfram | Alpha works with the help of calculations, and not, say, as a search engine. And for a while we wanted to use something with gears. But we also wanted the logo to resemble the long-standing Mathematica logo. This gave rise to one of those projects like “our general went crazy”: the creation of a gear mechanism from spiny forms.
A long-time user of Mathematica and Wolfram Language, a mechanical engineer from Hungary, Sandor Kabay helped us by offering spiked gears:
Returning to intersecting tetrahedra from version 2, he created something like this:

In 2009, 3D printers became very popular, and we thought it would be nice to make a logo for Wolfram | Alpha that can be printed. The hyperbolic polyhedron did not fit — spikes could break off and pose a threat. In figures like the spike 4th version, with "safe spikes", lacked elegance.
For a while, we clung to the idea of gears. But in the end they decided that it was worth taking another look at ordinary polyhedra. But which polyhedron can we choose?
Of course, there are an infinite number of possible polyhedra. But for our logo, we wanted to choose a symmetric and to some extent “correct” polyhedron. Five regular polyhedra (or “Platonic solids”) - whose faces are identical regular polygons - can be considered “the most correct” of all:

There are 13 more Archimedean solids - they have identical vertices, and regular polygons, although different Types:
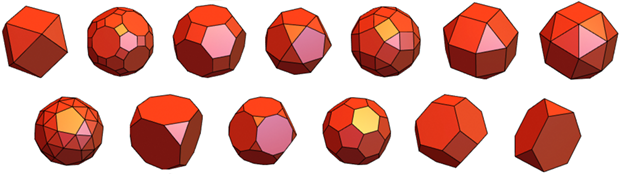
Types of "correctness" of polyhedra can be thought of in many ways. One example is “homogeneous polyhedra”, which is shown by a poster from The Mathematica Journal of 1993:

Over the years that Eric Vaystein was collecting a collection that had turned into MathWorld by 1999, he tried to include articles on as many of the most remarkable polygons as possible. In 2006, as part of the inclusion of various systematized data in Mathematica and Wolfram Language, we began to include data on polygons from MathWorld in them. As a result, after the release of version 6.0 in 2007, the PolyhedronData function appeared in it , which contained exhaustive data on 187 remarkable polygons:

In Mathematica and Wolfram Language it was always possible to generate regular polygons, but now it has become easier to do. With version 6.0, we also released the Wolfram Demonstrations Project, which quickly became replenished with various demonstrations related to polyhedra.
One of them was made by my daughter Katherine, when she was 10 years (today it continues to evolve in the directions associated with the geometry): a "multi-faceted koala", by all commonly used polyhedra of PolyhedronData []:

This is against this background that in 2009 th, we wanted to choose a polyhedron for Wolfram | Alpha. It was all decided on Friday, February 6, when I got down to business myself.
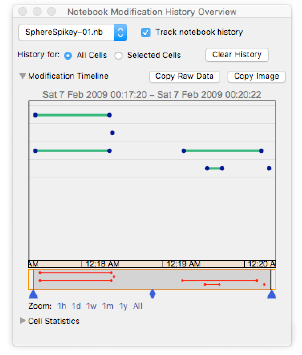
I still have that notebook, and it shows that at first I tried to realize the dubious idea of placing spheres in the vertices of polyhedrons:

But, as recorded in Notebook History , only two minutes later I switched to pure polyhedra — they were all orange. , which we then wanted to use for the logo:
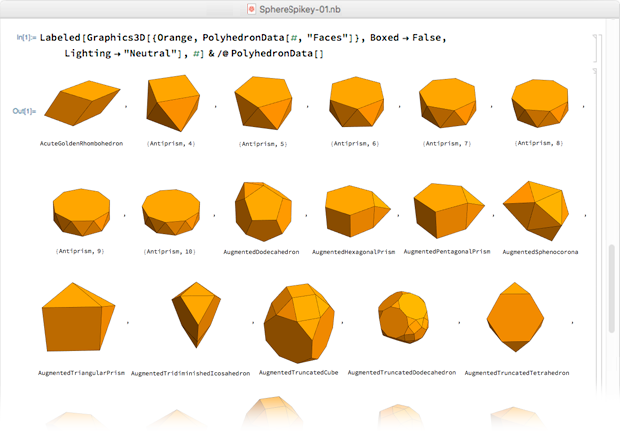
Polyhedra lined up in alphabetical order by name, and on the 28th line it appeared - a rhombic sixty-hexahedron.

A couple of minutes later, at 00:24:24, February 7, 2009, I found this rhombic hexagon and turned it into a symmetrical position, which we are using today:

I wanted to see how it would look in gray colors and as a silhouette, and four minutes later I usedColorSeparate to find out:
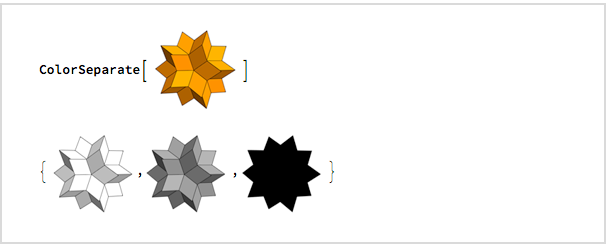
I immediately started writing an e-mail that I sent at 00:32:
I really like RhombicHexecontahedron. He has an interesting and very symmetrical form. It seems to me that its accuracy just suits us, and the silhouette looks quite reasonable.

Obviously, I simply copied RhombicHexecontahedron from my notebook (I doubt that I could write a hexagon [hexecontahedron] without errors). I know from my archives that this was the first time that I wrote the name of a polyhedron that was destined to be my favorite.
In the Wolfram Language it was very easy to get a picture of a rhombic hexagon, and play with it:
By Monday, it was clear that he had defeated a rhombic hexagon, and our graphic department was engaged in drawing it as a logo for Wolfram | Alpha. We tried different orientations of it, but in the end we settled on a symmetrical position “in full face”, chosen by me. (We also needed to choose the best “focal length” for the most appropriate angle).

Like our star icosahedron from version 1.0, the rhombic hexahedron has 60 facets. But somehow, thanks to the “five-petal” combinations, it looks much more elegant. Quite a lot of effort was spent on finding the shading of the edges so that the two-dimensional pattern correctly reflected the three-dimensional object. But soon we presented the first official version of our logo:

It quickly began to appear everywhere, and, as a tribute to our early ideas, often against a background decorated with gears:

A few years later, we slightly edited the shading of the faces, which led to the creation of the Wolfram | Alpha logo, which is still in use:

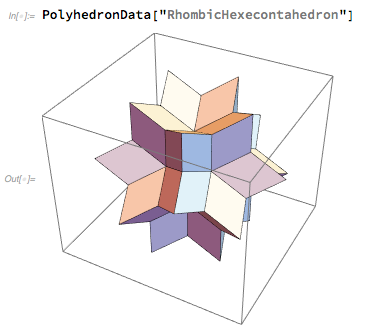
Rhombic hexahedron
What is rhombic hexahedron? In English, it is called hexecontahedron, since it has 60 faces, and ἑξηκοντα (hexcont) is a Greek word for “60”. Its faces are golden rhombuses , which are called so because their diagonals correspond with each other according to the golden section: φ = (1 + √5) / 2 & sime; 1.618:

The rhombic hexahedron is an interesting intermediate body between the icosahedron and the dodecahedron (with the icosododecahedron between them). The 12 internal vertices of a rhombic hexahedron form a regular icosahedron, and 20 external vertices form a regular dodecahedron. 30 "intermediate vertices" form the icosododecahedron, 32-hedron (it has 20 triangular and 12 pentagonal faces):
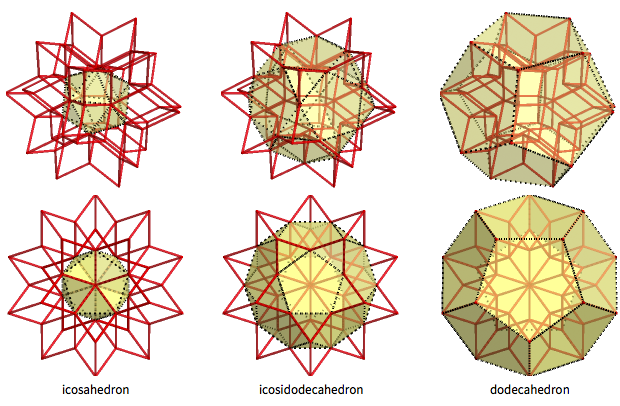
In total, the rhombic hexagon has 62 vertices and 120 edges (as well as 120-62 + 2 = 60 faces). It has three types of vertices (“internal”, “medium”, and “external”), corresponding to 12 + 30 + 20 vertices of the icosahedron, icosododecahedron, and dodecahedron. At these vertices, 3, 4, and 5 edges meet respectively. Each face has one “internal” vertex in which 5 edges converge, one external vertex where three edges meet, and two “intermediate” where 4 edges meet. The outer and inner vertices are the acute-angled vertices of the gold rhombus, and the intermediate vertices are obtuse-angled.
The angle at the peaked vertices of gold rhombus is 2 tan −1 (φ −1 ) ≈ 63.43 °, and at the blunt-pointed - 2 tan −1(φ) ≈ 116.57 °. Such angles make it possible to assemble a rhombic hexahedron from the Zometool designer using only red supports (as is the case with the dodecahedron):

Of the 120 edges of the rhombic sixty hexagon , 60 have “dihedral angle” at 4π / 5 = 144 °, and in 60 outer edges it equals 2π / 5 = 72 °. The angles tightened by the outer and inner vertices are π / 5 and 3π / 5.
To draw a rhombic hexahedron, you need to know the three-dimensional coordinates of its vertices. It is convenient to get them using the fact that the rhombic hexahedron is invariant with respect to the icosahedron group, so you can start with one gold diamond and simply add 60 matrices that form the three-dimensional representation of the icosahedron group. This, for example, gives the final coordinates of the vertices in {± φ, ± 1.0}, {± 1, ± φ, ± (1 + φ)}, {± 2φ, 0.0}, {± φ, ± ( 1 + 2φ), 0}, {± (1 + φ), ± (1 + φ), ± (1 + φ)} and their cyclic permutations with all possible signs.
In addition to the fact that the faces of a rhombic hexagon are gold rhombuses, a rhombic hexagon can be constructed from 20 gold rhombohedrons (all of which have six faces - gold rhombuses):

There are other ways to create a rhombic hexahedron from other polyhedra. It can be obtained from five intersecting cubes and 182 dodecahedron, contiguous faces:

Of the rhombic shestidesyatigrannikov can not lay out a continuous mosaic, but they are well engaged with each other (and, yes, I've seen dozens of paper Thornling evolved in such a way):

Also from them all sorts of rings and other configurations can be made:
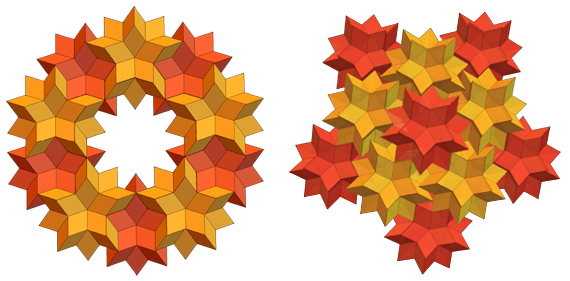
A close relative of the rhombic hexahedron (RS) is a rhombic thirty hexahedron (RT). RSH and RT have faces that are gold diamonds. But RS has 60 of them, and RT has 30 of them. Here's what a separate RT looks like:

Several RTs perfectly fit into the “pockets” of the RSH, and such things turn out:

Sandor Kabay, mentioned earlier, became interested in RSH and RT around 2002. And after the launch of the Wolfram Demonstrations Project, he, along with the Slovenian mathematician Isidor Hafner, added to the project more than a hundred demonstrations related to RSH, RT and many of their properties:

Paper models Spike
As soon as we decided that the Shipastic would be the RSH, we began to make it 3D models. Now it is very easy to do with the function Printout3D [PolyhedronData [...]], and on third-party resources you can find already calculated models .
In May 2009, when launching Wolfram | Alpha, we already had a lot of three-dimensional Shipipas on hand:

But, preparing for the first holiday season after this event, we decided to give everyone the opportunity to make their own three-dimensional Thorny. At first, we considered a variant with 20 rhombohedral magnets coated with plastic. But they came out expensive, and not very well stuck together.
This led us to the idea of making Thorn from paper or thin cardboard. Therefore, we first wanted to make a scheme that could be folded into Spike:

My daughter Katerina served as a tester (and still has a test sample), but it became clear that there were a lot of uncomfortable situations in the folding process, in which it is not clear how to go from one position to another. You can make a huge number of layouts (43 380) for the dodecahedron and icosahedron only - and we thought that maybe it would be possible to choose something better from them:

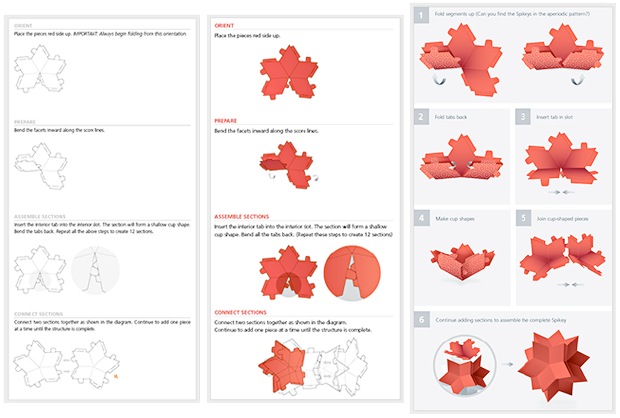
But, when we could not find such a scheme, we had a new (albeit obvious) idea: if the modelka keeps at the expense of the ears, why not make it out of several pieces? We quickly realized that for this we need to take only 12 identical pieces of this type:

With their help, we created our " sets for paper sculptures ": The

writing task was an easy task to understand, but after several iterations the instructions became well-developed and simple:
And after the paper Thorns went to the people, our users began to send us all sorts of Thorn images on the ground:

Path to the rhombic hexahedron

Multifaceted cube from ancient Egypt
It is not known who first described the Platonic solids. Perhaps the Pythagoreans (who lived near such large deposits of many-sided pyrite crystals) did this . Perhaps it was done by someone long before them. Perhaps it was a contemporary of Plato, Teethet Athens . But, in any case, by the time of Plato (c. 400 BC), five Platonic solids were known. And when Euclid wrote his "Elements" (c. 300 BC), one of the pillars of this work was proof of the absence of other regular polyhedra. This proof is known for taking the most steps from Euclid’s original axioms — 32.
Platonic solids used for dices and ornaments. But they also were assigned a central role in thinking about nature - for example, Plato assumed that in some sense everything could consist of them: earth from cubes, air from octahedra, water from icosahedra, fire from tetrahedra, and heaven (“ether” ) from dodecahedra.
What about other polyhedra? In the 4th century AD Papp of Alexandriawrote that a couple of centuries before this, Archimedes discovered 13 other "regular polyhedra" — apparently, what is now called Archimedean bodies — although the details of this have been lost. And for a thousand years, little has happened to polyhedra. But in the 15th century, with the beginning of the Renaissance, polyhedra suddenly became fashionable again. Leonardo da Vinci and Albrecht Dürer regularly used them in art and design, rediscovering some of the Archimedean bodies — as well as discovering new polyhedra, such as the icosododecahedron.
But the biggest step forward for polyhedra was the work of Johann Kepler.at the beginning of the seventeenth century. It all started with an elegant, albeit completely incorrect theory. Kepler, on the basis of theological prerequisites, believed that the Universe should be created with mathematical precision, and suggested that the six planets known at that time move along nested spheres inscribed and described around five Platonic bodies:

In his 1619 book Harmonices mundi , “Harmony of the World”, Kepler argued that many features of music, planets and souls work according to similar geometric relationships and principles. To confirm the arguments, Kepler studied polygons and polyhedra, especially interested in objects that make up complete sets, such as Platonic solids.
He studied the "contact polyhedra", which can pave the plane - and found, for example, " monstrous tiles", as he called them (consisting of pentagons, pentagrams and decagons). He studied the" star polyhedra "and found various star-shaped versions of the platonic solids (and Kepler's body - Poinsot ). In 1611 he published a small book about the six-sided structure of snowflakes written in as a gift for the new year to one of his patrons. In this book, he discussed three-dimensional packaging of spheres (and spherical atoms), proposing the hypothesis that the densest packaging of balls in three-dimensional space (we regularly observe its realization in fruit packaging in stores) is a face-centered cubic packaging (this hypothesis was formally proved only after 2000 - with the help of Mathematica).
In different packages of Kepler, different polyhedra are hidden. Let's start with any sphere, take its neighbors and connect their centers to get the vertices of the polyhedron. In the densest packaging, Kepler of any sphere touches 12 others, and from their centers a cuboctahedron with 12 vertices and 14 faces is obtained. But Kepler described another package, 8% less dense, in which each sphere is affected by 8 others, and another 6 are very close. If we connect their centers, we get a rhombic dodecahedron, with 14 vertices and 12 facets:

Upon discovering this, Kepler began a search for other rhombic polyhedra. In the rhombic dodecahedron that he found, the rhombuses consisted of pairs of equilateral triangles. But by 1619, Kepler also studied gold diamonds - and found a rhombic thirty-square, after which he painted his beautiful image in his book, next to the rhombic dodecahedron:

Kepler immediately found the use of rhombic polygons: he wanted to use them and a cube to build a model of nested spheres , approaching the orbits of the four moons of Jupiter, discovered by Galileo in 1610th.
Why didn't Kepler open a rhombic hexahedron? I think he came quite close to him. He studied the non-convex stellate polyhedra. He considered rhombic polyhedra. But, apparently, for his astronomical theories, there was enough of a rhombic thirty-hexahedron, after which he ceased his search.
As a result, of course, the laws of Kepler, unrelated to the polyhedron, became the main contribution to astronomy, which survived it. But Kepler’s work on the polyhedron — even if carried out within the framework of an incorrect physical theory — remains an eternal contribution to mathematics.
Over the next three centuries, more polyhedra of various regularities were found - and by the beginning of the XX mathematicians already knew many of their types:

But, as far as I can tell, the RSH was not among them. His opening was waiting for workHelmut Unkelbach . He was born in 1910, defended his doctoral degree in mathematics at the University of Munich in 1937 (although he first studied physics). He wrote several papers on conformal mapping, and - possibly due to the study of polyhedron mapping - in 1940 he published in German the paper “Rib-symmetric polyhedra”.
He explained that his goal was a comprehensive study of all possible polyhedra that satisfy a special new definition of correctness: all edges have the same length, and are in the plane of symmetry of the polyhedron. The main result of the work was a table with 20 different polyhedra of such a property: Clickable Most of them were already known. But Unkelbach identified three of them that he considered new: two
a hexacacystahedron (or disdacidodecahedron), two hexaciciosahedron (or disdakistriacontahedron) and what he called the Rhombenhexekontaeder, or rhombic hexahedron. And he obviously considered the RSH to be his main achievement, and included a photo of his model, made by him:

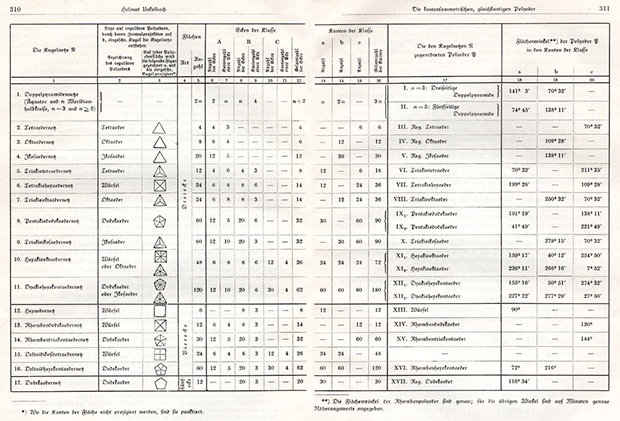
How did he get the RSH out? He started with the dodecahedron, and defined two of its planes of symmetry:
Then divided each of its faces:

Then, in fact, squeezed the centers of each of the faces by a distance equal to the usual distance to the center multiplied by some α:

For α <1, the resulting faces did not intersected. But for most α values, their sides were not equal. This happens only in a specific case - when the final polyhedron exactly coincides with RS.
Unkelbach considered his 1940 work "warming up" for a more extensive study of "k-symmetric polyhedra" with less stringent requirements for symmetry. But, of course, it was a miracle that a mathematical journal was published in Germany after the start of the Second World War - shortly after this publication Unkelbach was called to the front, where he developed acoustic torpedoes for the German fleet for several years.
He did not publish more work on polyhedra, and died in 1968. After years he returned to a conformal mapping, and began publishing on the theory of voting , considering it the key to creating a well-functioning democracy, and thinking that mathematicians were obliged to make people started using it.
But even appearing in the work of 1940, RSH could have lived there forever, if in 1946 a certain Harold Scott MacDonald Coxeter had not written a short review of this work for the relatively new journal American Mathematical Reviews. In his review, the polyhedra mentioned in the work are listed, as a naturalist can list the new species discovered by him in the expedition. The main thing that he described there was “a remarkable rhombic sixty-hexahedron”, and mentioned that “the shape of its faces coincides with the shape of the faces of the thirty-hexahedron, from which it was obtained by giving a star shape”.
Polyhedra were not a popular topic in mid-20th century mathematics, but Coxeter was their main proponent — and in one way or another was connected with everyone who studied them. In 1948, he published the book The Right Polytopes. It systematically describes various families of regular polyhedrons, in particular, the great stellar thirty , which in fact contains RS:

But in his book, Coxeter does not mention RS directly, and although he was honored to be mentioned by some fans of polyhedra, RSH remained little known.
Quasicrystals
Crystals have always been important examples of polyhedra in nature. But by the XIX century, when atomic theory was gaining more and more recognition, scientists began to conduct more and more serious research in the field of crystallography and the arrangement of atoms in crystals. Polyhedra began to appear frequently, in particular, in representations of the geometry of repetitive atomic blocks (“cells”) in crystals.
By 1850, it was known that there are only 14 such geometries - among them there are those based on the rhombic dodecahedron. They are notable for the presence of second, third, fourth, or sixth symmetry in them - which, in fact, is a consequence of the fact that space can be filled only with certain polyhedra, just as a regular polygon like squares can fill a two-dimensional plane, triangles and hexagons.
What about other non-crystalline materials — for example, liquids or glass? Since the beginning of the 20th century, people have been interested in the possibility of the presence of at least approximate fifth order symmetries there. It will not be possible to fill the space with correct icosahedrons, but it will probably be possible to create twenty-segment parts of space with small intervals between them.
This question remained unresolved until the 1980s, when electron diffraction crystallography on a rapidly cooled aluminum-manganese alloy demonstrated the presence of five-fold symmetry. Theories of achieving such symmetry already existed, and after a few years, images made with an electron microscope appeared, on which particles having the shape of a rhombic thirty-hexa were visible:

And, while people imagined how these thirty-hexa can be combined with each other, a rhombic hexahedron also appeared - in the form of a “hole” in a cluster of 12 rhombic thirty-polyhedra:

At first it was called a 20-pointed star. But then it was associated with descriptions in the literature on the polyhedron, and identified as RS.
Meanwhile, the idea to create objects from rhombic elements gained more and more popularity. Michael Longue-Higgins, an oceanographer and ocean wave expert, joined the popular hobby, and in 1987 he patented a toy based on rhombohedral elements from which he could assemble a Kepler star (RS) or a Kepler ball (a thirty-sided rhombic ):

And - although I only found out about it now - the rhombohedral blocks, which we considered in 2009 as an option for creating “Shipipikov”, were actually produced by the company Dextro Mathematical Toys (Rhombo.com), which worked on the base of the Long-Higgins house in San Diego
The question of successfully filling a space with three-dimensional figures — or even a plane with two-dimensional figures — is rather complicated. Since the 1960s, it has been known that, in the general case, the problem of whether a certain set of forms can fill a plane is insoluble. (In principle, it is possible to check whether 1000 of these forms can be composed with each other, but the more forms we consider, the more computing resources this will require).
People like Kepler probably assumed that if a set of forms could fill a plane, then this could be done in a repeating pattern. However, after it became clear that, in general, this problem is not solved, in 1974 , Roger Penrose came up with two forms that can fill the plane without repeating patterns. By 1976, Penrose (and Robert Ammann) came up with a simplified version of these forms:

And, yes, these forms have the form of diamonds, although not gold. But with angles of 36 °, 144 ° and 72 °, 108 °, they have 5-fold and 10-fold symmetry.
These diamonds can not lay out the repeating patterns. But it turns out that they can lay out a pattern built in a systematic nested way:
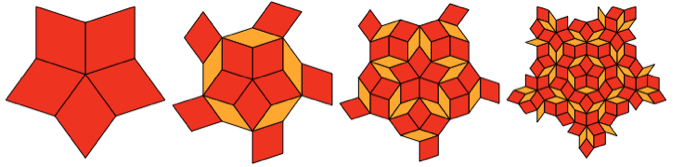
And, yes, the middle part of the 3rd step is very similar to the flattened Thorny. But it does not completely coincide with it, external diamonds have a slightly different format.
However, a close connection between them does exist. Imagine that we are not starting from a plane, but from a half of a three-dimensional rhombic thirty-diamond consisting of golden rhombuses:

From above, it looks exactly like the beginning of a Penrose nested mosaic. If we continue this process, we get this mosaic:

If you look at it “from the side,” you can see that these are still identical gold diamonds:
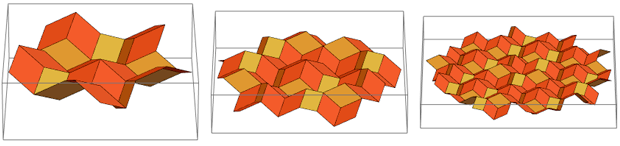
By making four of these “Wieringa roof” roofs, you can get just RS:

What is the connection between these nested structures and the real way of forming physical quasicrystals? It's not clear yet. But it is rather interesting to watch how hints on RSH appear in nature.
Historically, it was precisely due to the discussion of quasicrystals that Sandor Kabai began to study RS with Mathematica, which led Eric Vaystein to their discovery, which led to their inclusion in Mathematica and the Wolfram Language, which led to the fact that I chose one of them for our logo. In honor of this, we print a Penrose mosaic inside our paper Thorny:

Flattening Thorn
Our Spike for Wolfram | Alpha broke into the world in 2009 with the release of Wolfram | Alpha. But we also have our Thorny for Mathematica, which has long been developing and evolving. Therefore, when we built our new European headquarters in 2011, two Thoroughts competed for their presence.
Our long-time art director Jeremy Davies came up with the following: take one of the Shipipics, and “idealize” it, using his skeleton alone. The decision to start with RS was easy. But then we flattened it, and so the first version of the now-familiar logo appeared:

Brazilian surprise
When I started this article, I thought that the whole story would end there. After all, I have already described how we chose RS for ourselves, and how mathematics invented it. But before I finish writing, I decided: “I’ll see all the letters about Thorny for all the years, just to make sure that I didn’t miss anything.”
And then I noticed an e-mail from June 2009 from the Brazilian artist Yolanda Cipriano. She wrote that she saw an article about Wolfram | Alpha in a Brazilian news magazine, drew attention to Thorny, and provided a link to her site. Since then, more than 9 years have passed, but I still followed this link, and was amazed to see the following:

I continued to read her letter: “We have this object in Brazil called Giramundos or“ flower mandakara ”and its as an artistic Ornaments made from napkins.
What?! In Brazil, there is a tradition associated with Thorpastic, and in all the years we have not heard of it? Soon I discovered his images on the net. A small part of the models was made of paper, the majority was made of fabric - but there were a lot of them:

I wrote to my Brazilian friend who worked on the first versions of Wolfram | Alpha. He quickly replied: “These objects really seem familiar. To my shame, I didn’t have enough desire to compare two and two, ”and sent me pictures from the local catalog of works of art and crafts:

The hunt began: what were these objects and where did they come from? Someone from our company said that his great-grandmother from Chile crocheted such things, and always made them tail. We began to get involved with people posting photos of “folk spines” on the web. Quite often it turned out that they bought their copies in stores. But sometimes people said they knew how to do them. And they all had almost the same story: they learned it from their grandmothers.
The typical way to assemble a folk spike - at least in our time - is to cut 60 rhombuses out of cardboard. Then each needs to be wrapped in fabric, and stitched together:

But here a mathematical problem immediately arises. Is it true that these people correctly mark and cut out gold diamonds with a 63 ° angle? Usually not. They make diamonds with 60 ° of pairs of equilateral triangles - this is the standard diamond shape used in the manufacture of quilt blankets. So how do Thorn Spikes come out? Well, the difference between 60 ° and 63 ° is small, and if you stitch the edges, there will be enough space for maneuver between them, so you can simply make a polyhedron without achieving absolutely accurate angles. (There are also quasi-thorny, which, as in the Unkelbach construct, have diamonds instead of diamonds instead of facets, but sharp “outer triangles”).
Folk spines on the Internet are designated differently. Most often - Giramundos. Often they are called Estrelas da Felicidade ("stars of happiness"). What confuses them is that they are sometimes called “Moravian stars,” but in fact Moravian stars are much more acute polyhedra (most often made of rhombic cuboctahedron) that have recently gained popularity as lamps.
Despite a long investigation, I still do not know the whole history of folk spines. This is what I discovered. Firstly, it is mainly present-day national spines that are concentrated in Brazil (although we have stories about their appearance in other places). Secondly, the tradition looks quite old, it definitely appeared long before the 20th century, and perhaps a few centuries before. As far as I can tell, it is passed on from mouth to mouth, as is usually the case with folk art, and I haven’t found any real historical documents on this subject.
The best information was given to me by someone Paula Guerra, who sold folk spikes in a tourist cafe she ran ten years ago, located in the historic city of São Luis do Paraíting. She said that people from all over Brazil came to her café, saw folk spines, and said something like, “I have not seen such pieces for 50 years.”
Paula herself learned about the folk spines (she calls them “stars”) from an older woman who lived on a family farm that had been making them since she was a girl, and learned from her mother. Her process — apparently typical — was to get cardboard anywhere (initially it was something like hat boxes), cover the pieces with a cloth, and sew them together, getting an object about 15 cm in size.
How old is the folk spike? This can only be assessed by oral tradition. We found several people who saw how the spines were made by their relatives born in the 1900 area. Paula said that ten years ago she met with an 80-year-old woman who told her that when she grew up on a coffee farm 200 years ago, there was a whole regiment with folk tenes made by four generations of women.
A part of the history of national spike, apparently, revolves around the traditions transmitted from mother to daughter. It is said that mothers often made spines as wedding gifts for their daughters. Usually, the spikes were made from scraps of clothing and other things that remind daughters of childhood - something like how quilts are made today for children going to college.
However, there was another twist with folk spikes: often before stitching up the toy, the mother put money inside that her daughter could use in critical cases. And the daughter kept her spike together with her sewing accessories, where her husband would hardly have found him. Some spines were used as pin cushions — which may have served as an additional obstacle for husbands.
In which families was the tradition of making folk spines maintained? Since about 1750, in the rural areas of Brazil, there have been many coffee and sugar plantations, remote from the cities. Until about the 20th century, farmers often took girls as brides - often very young, up to 13 years old - from distant cities. Perhaps these brides - usually from good families of Portuguese origin, with a relatively good education - had with them folk spines.
Apparently, over time, the tradition has spread to families poorer, and mostly there remained. But somewhere in the middle of the 20th century — probably, when roads began to appear in the country, urbanization started, and people began to leave the farms — the tradition almost died out. However, in the rural schools of southern Brazil in the 1950s, girls in art classes were trained in making folk spines with a special slot for use as piggy banks.
Folk shipastiki have a different history in different parts of Brazil. In the southern border regions (near Argentina and Uruguay) there is a tradition in which “the star of St. Miguel "(she is the people's spike) was made in the villages by female fortune-tellers (ie," witches "), who during the manufacture of the toy had to think about the health of the patient.
In other parts of Brazil, toys were often called the names of flowers and fruits, which slightly reminded her. In the northeast - Flor Mandacarú (by the name of the flowers of cactus). In tropical wetlands, Carambola (in honor of the fruit of carambola, which is sometimes called "tropical stars"). In the central wooded regions - Pindaíva (in honor of the red spiny fruit).

But most often the folk spines are called Giramundo - a rather old Portuguese word that literally means “a whirling world.” Apparently, toys were used as amulets, bringing good luck by their rotation in the wind. Tails began to attach them recently, but, apparently, they were taken to hang in houses, perhaps for holidays.
It is often unclear which of the traditions that gave rise to spiny was original, and which appeared recently. At the parade in honor of the Epiphany (the local name is “the day of the three kings”) in Sao Luis do Paraytinga, national shipasty were used as a symbol of the Bethlehem star - but this, apparently, is not a very ancient tradition, and clearly does not show connections with religion.
We found several examples of folk spines that appeared at art exhibitions. One of them, held in 1963, and dedicated to the folk art of northeastern Brazil, was organized by the architect Liina bo Bardi. The other one, where the largest of the three-dimensional spines I had seen was exhibited, was organized in 1997 by the architect and designer Vlavio Imperio:

So where did the national spipics come from? That I do not know so far. They could appear in Brazil, could come from Portugal or another part of Europe. The fact that for their manufacture used pieces of fabric and sewing, there may be arguments in favor of their African or Indian origin.
One modern artisan who made spines, said her great-grandmother — who made such toys and was born at the end of the 19th century — comes from a region of Italy called Romagna (and one said that she learned to make spikes from her grandmother, who originated from French Canadians). I think it is quite possible that the folk shipasty were once common in Europe, but many generations died out, and this tradition was not preserved there. And although quite a few different polyhedra appear in European paintings of previous centuries, I don’t know about one image of Thorny among them (also I didn’t see Thorniness in Islamic art).
But I’m pretty sure that folk spines have one point of origin. Such a thing would hardly have been invented twice.
I must say that this is not my first hunt in the field of art. More successful was the search for the first nested pattern ( Sierpinski ) - which eventually led me to the crypt in the Italian church, where I watched how this pattern was gradually discovered using the example of a stone mosaic dating from the 13th century.
So far, Thorny has not given up so easily - and the fact that it was mainly made from a fabric that does not survive as well as a stone complicates the situation.
Spike come to life
Whatever its origin, Shipastic is well playing the role of a strong and decent logo. But sometimes it is fun to revive Thorny - and over the years we have made various personified Thorny on various occasions:

When using Wolfram | Alpha, the system usually shows geometric Thorny. But sometimes your request enlivens it - for example, requests for π on pi day:
blog.stephenwolfram.com/data/uploads/2018/12/spikey-lives-happy-pi-day-video.mp4
Thorn forever
Polyhedra are eternal. They can be seen in a 500-year-old image that looks as clear and modern as a polyhedron on my computer.
I spent quite a lot of my time searching for abstract computing things (for example, cellular automata). They also have some timelessness. But for them I did not find any historical evidence. As abstract objects, they could be created at any time. But they appeared today thanks to the conceptual platforms and tools we have - and nobody has seen them before.
The rich history and constancy of polyhedra are thousands of years old. Appearance they resemble precious stones. To discover a regular polyhedron of a certain kind is the same as to discover a gem in a geometric universe of all possible forms.

RSH is one of these amazing stones, and, studying its properties, I began to appreciate it even more. But it’s also a gem with a human history — and it’s terribly interesting to see how such an abstraction, like a polyhedron, can unite people from all over the world with such different histories and goals.
Who first came up with the rhombic hexahedron? We do not know, and may never know. But now that we have it, it will remain with us forever. My favorite polyhedron.
