Heaps. Part 1. Binomial heap
Hello, Habrosociety!
On the habr there is a description of many interesting data structures, such as segment trees, ducha, etc. If you are interested in complex data structures, then welcome to cat! In my series of articles, I will consider different types of heaps and how to put them into practice:
1) Binomial heap
2) Left heap
3) Fibonacci heap
4) Putting these data structures into practice
Problem statement:
Build a data structure in which many of our objects will be stored (different depending on the task), each object will have a key field, by which we can quickly find the minimum element. The following operations should be possible for this structure:
Many are familiar with the simplest ways to implement this structure, such as an array :) and a binary heap. I will not dwell on them in detail because of their simplicity and common knowledge.
As you know, for a binary heap, the asymptotic behavior of the above operations is as follows:
I will not describe the algorithm of the binary heap, as it has been repeatedly described everywhere, including on Habré. For those who are not familiar with the binary heap, I would recommend to familiarize yourself with it before continuing reading.
Next, consider a more interesting data structure called the binomial heap .
Binomial Heap A
binomial heap is a set of binomial trees with some restrictions. We will introduce them a bit later.
A binomial tree is a tree that is specified recursively:
B i is B i - 1 , in which the tree B i - 1 was made the left son of the root .
B 0- it's just the top.
Examples for B 0 , B 2 , B 3 :
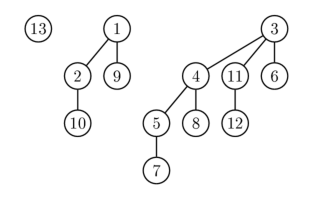
The binomial tree (B k ) has a number of interesting properties :
T.1. 2 k vertices of
T.2. Tree height k
T.3. C i k vertices of depth i (which is why they are called binomial: C i k is a binomial coefficient).
T.4. The children of the root are B, B k - 2 , ..., B 0 - in that order.
T.5. Maximum vertex height in binomial tree O (log N)
Provedproperties by induction. I invite readers to conduct the proof themselves, for a better understanding of trees.
So, now back to the binomial heaps . A binomial heap is a set of binomial trees, with the following restrictions:
1) The heap property is preserved in each of the binomial trees.
2) There are no two trees of the same size
3) The trees are ordered by size.
Let's talk about how the binomial heap will be stored in the program. We will use the “left son - right brother” method. We will store the root list (
immediately note:
Property H.1:
Length
For the proof, it is enough to note that due to T.1, the presence of the tree B k in the binary notation of the number.
Let's move on to the description of operations that can be performed with binomial heaps:
Make
Task : create an empty heap.
Algorithm : create an empty list
Difficulty : obviously, the running time is O (1).
Merge
Challenge: combine 2 heaps into 1.
Algorithm : first combine the root lists of heaps into 1 root list, maintaining ordering by degree. The algorithm is similar to merging 2 arrays in mergeSort:
We store by the pointer to the beginning of the lists and in the resulting list write the minimum of them, the one from which we just wrote is shifted to the next. Next, we go from beginning to end of the new received root list and merge trees of the same size into 1. There may be cases:
1) Only 2 trees of the same size. Then combine them.
2) 3 trees of the same size. Combine the last 2.
When combining two trees, you only need to look at the root of which one has the smaller key and make the other tree the left son of the root of this tree.
An example of what happens after combining two heaps:
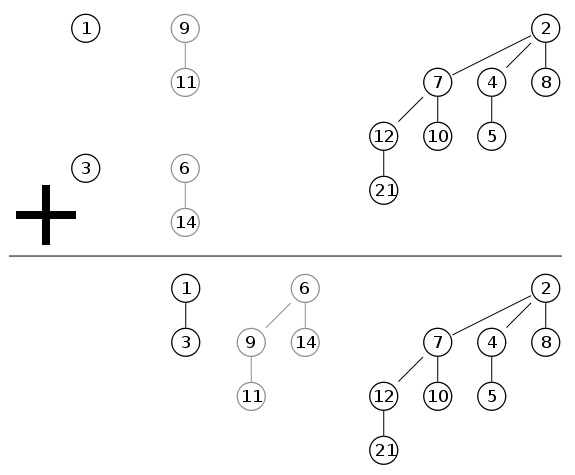
Complexity : O (
In one pass (O (log N)) we get the combined binomial tree. We get that the total complexity is O (log N).
Insert
Task : insert a new element into the heap.
Algorithm : Create a bunch of one element and combine with our bunch.
Difficulty : O (1) + O (log (N)) = O (log (N)).
Minimum
Task : find the minimum on the heap.
Algorithm : obviously, the minimum is in the root list, that is, to find it you need to go through the root list.
Difficulty : O (
ExtractMin
Task : remove the minimum element.
Algorithm : find it with
Difficulty : since each operation in extracting a minimum works for O (log N): O (log N) + O (log N) + O (log N) = O (log N)
Decrease
Task : reduce the data value at this vertex.
Algorithm: decrease the value at the top. Then the heap property will be possibly violated for our peak and its ancestor, then we will change their places. We continue the process until our peak “pops up” in its place. The algorithm works the same as the one in the binary heap.
Difficulty : In the worst case, our vertex will pop up to the root, that is, we will perform O (log N) actions (the vertex at each step “pops up” one level higher, and the binomial tree height is T.5 O (log N))
Delete
Problem : delete an arbitrary element.
Algorithm : First, reduce the
Difficulty : O (log N) + O (log N) = O (log N)
Conclusion.
We examined the data structure of the binomial heap and proved its asymptotic behavior.
In the next article, based on the binomial heap, we will build a slightly more complex data structure, namely the Fibonacci heap.
You can play around with binomial heaps at rain.ifmo.ru/cat/view.php/vis/heaps/binomial-2001
You can read more in T. Cormen's "Algorithms: Construction and Analysis."
Thank you all for your attention, and see you soon!
On the habr there is a description of many interesting data structures, such as segment trees, ducha, etc. If you are interested in complex data structures, then welcome to cat! In my series of articles, I will consider different types of heaps and how to put them into practice:
1) Binomial heap
2) Left heap
3) Fibonacci heap
4) Putting these data structures into practice
Problem statement:
Build a data structure in which many of our objects will be stored (different depending on the task), each object will have a key field, by which we can quickly find the minimum element. The following operations should be possible for this structure:
Make- creating a new empty heap, Insert- inserting a new element into the heap, Minimum- the minimum key, ExtractMin- extracting the minimum, Merge- merging 2 heaps, Decrease- reducing the key, Delete- deleting the object. Many are familiar with the simplest ways to implement this structure, such as an array :) and a binary heap. I will not dwell on them in detail because of their simplicity and common knowledge.
As you know, for a binary heap, the asymptotic behavior of the above operations is as follows:
Make- O (1) Merge- O (N) Insert- O (log N) - where N is the number of elements in the heap. Minimum- O (1) ExtractMin- O (log N) Decrease- O (log N) Delete- O (log N)I will not describe the algorithm of the binary heap, as it has been repeatedly described everywhere, including on Habré. For those who are not familiar with the binary heap, I would recommend to familiarize yourself with it before continuing reading.
Next, consider a more interesting data structure called the binomial heap .
Binomial Heap A
binomial heap is a set of binomial trees with some restrictions. We will introduce them a bit later.
A binomial tree is a tree that is specified recursively:
B i is B i - 1 , in which the tree B i - 1 was made the left son of the root .
B 0- it's just the top.
Examples for B 0 , B 2 , B 3 :

The binomial tree (B k ) has a number of interesting properties :
T.1. 2 k vertices of
T.2. Tree height k
T.3. C i k vertices of depth i (which is why they are called binomial: C i k is a binomial coefficient).
T.4. The children of the root are B, B k - 2 , ..., B 0 - in that order.
T.5. Maximum vertex height in binomial tree O (log N)
Provedproperties by induction. I invite readers to conduct the proof themselves, for a better understanding of trees.
So, now back to the binomial heaps . A binomial heap is a set of binomial trees, with the following restrictions:
1) The heap property is preserved in each of the binomial trees.
2) There are no two trees of the same size
3) The trees are ordered by size.
Let's talk about how the binomial heap will be stored in the program. We will use the “left son - right brother” method. We will store the root list (
root_list, its length root_list.length), in which there will be the roots of binomial trees, in order of increasing height. Each vertex will have the following fields:data- data that is stored in the vertex (we find the minimum from them) right- the right brother child- the left son degree- the degree of the vertex (obviously the trees in the binomial heap are ordered by this field) We immediately note:
Property H.1:
Length
root_list.length= O (log N ), where N is the number of elements in the heap. For the proof, it is enough to note that due to T.1, the presence of the tree B k in the binary notation of the number.
Let's move on to the description of operations that can be performed with binomial heaps:
Make
Task : create an empty heap.
Algorithm : create an empty list
root_list. Difficulty : obviously, the running time is O (1).
Merge
Challenge: combine 2 heaps into 1.
Algorithm : first combine the root lists of heaps into 1 root list, maintaining ordering by degree. The algorithm is similar to merging 2 arrays in mergeSort:
We store by the pointer to the beginning of the lists and in the resulting list write the minimum of them, the one from which we just wrote is shifted to the next. Next, we go from beginning to end of the new received root list and merge trees of the same size into 1. There may be cases:
1) Only 2 trees of the same size. Then combine them.
2) 3 trees of the same size. Combine the last 2.
When combining two trees, you only need to look at the root of which one has the smaller key and make the other tree the left son of the root of this tree.
An example of what happens after combining two heaps:

Complexity : O (
root_list1.length) + O ( root_list2.length) = runtime (by property H.1) = O (log N). In one pass (O (log N)) we get the combined binomial tree. We get that the total complexity is O (log N).
Insert
Task : insert a new element into the heap.
Algorithm : Create a bunch of one element and combine with our bunch.
Difficulty : O (1) + O (log (N)) = O (log (N)).
Minimum
Task : find the minimum on the heap.
Algorithm : obviously, the minimum is in the root list, that is, to find it you need to go through the root list.
Difficulty : O (
root_list.length) = O (log (N)).ExtractMin
Task : remove the minimum element.
Algorithm : find it with
Minimum. Remove it from the root list. From the inverted list of his children, make root_list for the new heap (H 1 ) and combine the original heap with H 1 . Difficulty : since each operation in extracting a minimum works for O (log N): O (log N) + O (log N) + O (log N) = O (log N)
Decrease
Task : reduce the data value at this vertex.
Algorithm: decrease the value at the top. Then the heap property will be possibly violated for our peak and its ancestor, then we will change their places. We continue the process until our peak “pops up” in its place. The algorithm works the same as the one in the binary heap.
Difficulty : In the worst case, our vertex will pop up to the root, that is, we will perform O (log N) actions (the vertex at each step “pops up” one level higher, and the binomial tree height is T.5 O (log N))
Delete
Problem : delete an arbitrary element.
Algorithm : First, reduce the
Decreasevalue at the vertex to the minimum possible. And then delete the minimum on the heap ( ExtractMin). Difficulty : O (log N) + O (log N) = O (log N)
Conclusion.
We examined the data structure of the binomial heap and proved its asymptotic behavior.
In the next article, based on the binomial heap, we will build a slightly more complex data structure, namely the Fibonacci heap.
You can play around with binomial heaps at rain.ifmo.ru/cat/view.php/vis/heaps/binomial-2001
You can read more in T. Cormen's "Algorithms: Construction and Analysis."
Thank you all for your attention, and see you soon!
