Keygenme analysis from TPoDT # 2
Good day to all.
This is me again, and again brings the topics of reverse engineering to the masses. Since, for some reason, I can’t cover the analysis of commercial protectors or programs in my articles, so for today our experimental rabbit will be the keygenme from TPoDT group. Not to say that it’s difficult, but it was not a pity to spend a couple of hours on it.
For those who are not in the know: keygenme is a type of program that is created by some crackers to analyze them by others. As a rule, the goal is to show some interesting mathematical algorithm or unusual code protection.
You can download keygenme here. It is worth paying tribute to the authors - keygenme is not packed in any way, which saves us from unnecessary gestures. And apparently the authors even bothered to make a nice interface.
We load it into the debugger, and set breakpoints on the standard WinAPI functions used to get the text from the input fields: We
There are no unpleasant surprises, and we immediately stop at
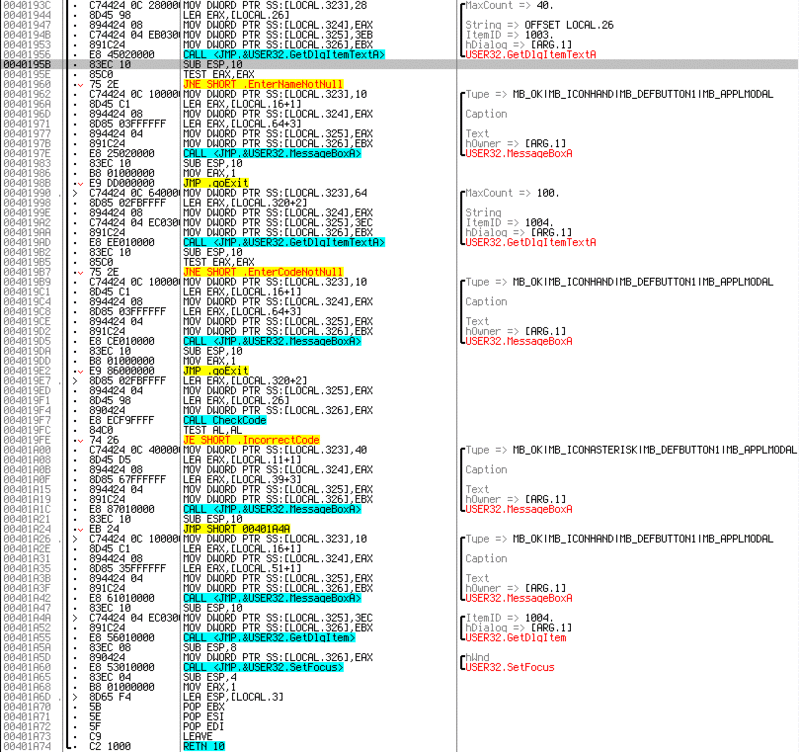
As you can see, the text is being read from the input fields, and if they are empty, then the MessageBox with errors is displayed. Below you can see the entrance to the function
But we are interested in the algorithm itself, and therefore we go into
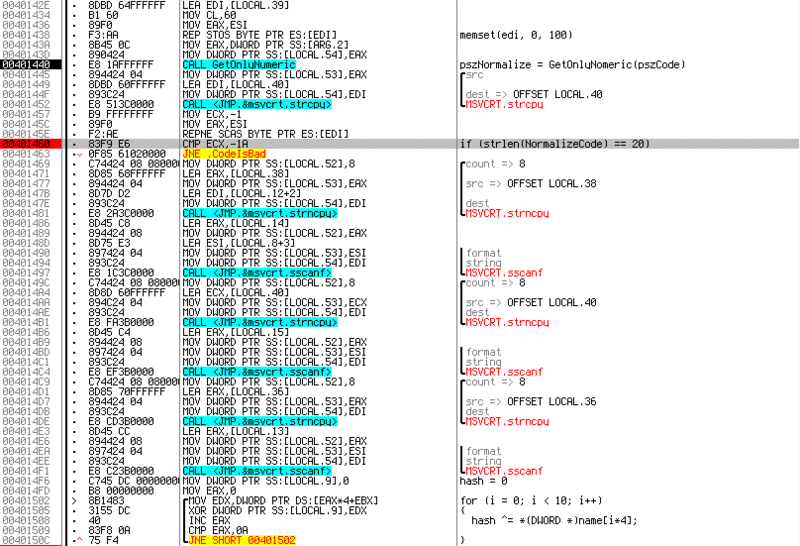
The code is pretty clean and easy to read. The first step is to call a subprocedure called by me
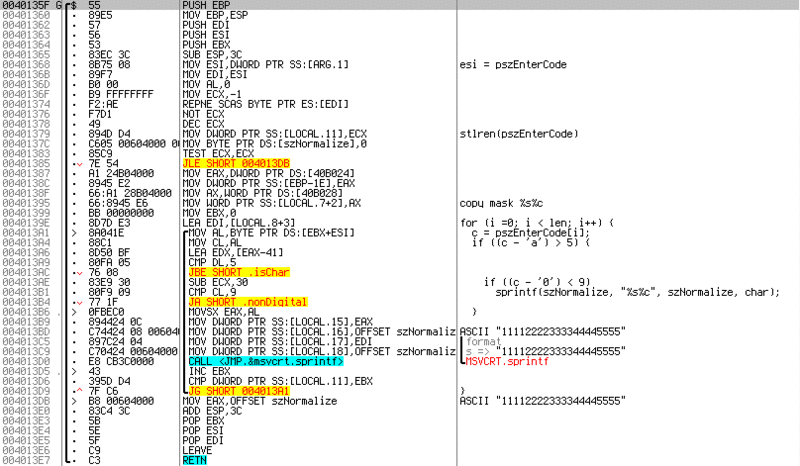
For C enthusiasts, I specifically made comments on a C-like pseudo-code. The code in the loop reads the entered line and if the character does not lie in the range
Let's go back to the function code
Subsequent function calls
Personally, when researching programs, I first look superficially at what she does, tracing the code, and then I analyze the necessary sections in the opposite direction from the checks.
In this case, the decision will be correct at which
Let's start with
In general,
This is my variation; hyphens can also be arranged differently.
So, we learned the right part of the condition, now let's move on to the left - to calculate EDI.
I will describe briefly what happens after
Now let's see what happens to
which, to obtain the original number from KEY1, can be reversed as follows:
At this stage, we will not try to substitute numbers; first, we will look at the rest of the checks.
There are three of them at once in this screenshot. The first almost repeats the previous one. Of the differences, we can distinguish a change in the calculation algorithm KEY2
Which are also easily converted to
And also, the half-byte indexes have changed. Now 5 and 6 are taken from KEY2 and (!) 1, 2 from KEY1. That's why I said that it’s not worth picking up numbers, since they are still used further according to the algorithm. In further checks, key numbers are no longer generated, but two received KEY1 and KEY2 are used.
The third check multiplies 0,1,4 and 5 half-bytes of KEY1.
At the very bottom of the screenshot, at the address
The first two of them are of the same type, and simply choose their half-bytes from the key numbers for multiplication. Therefore, I will not repeat myself. The verification located at the address deserves more attention
The team
Now a little math. At the very beginning, we saw that the number with which the comparison is made in the checks is CRC * 15. And since we found above that CRC = 0x5B, it is not difficult to obtain SUM = CRC * 15 = 0x555 = 1365 (10).
In each check, when multiplying half-bytes, 4 operands are always used, which means that we must factor 1365 into 4 factors. If the divisibility of 3 and 5 is visible by eye, then the remaining 7 and 13 are no longer so obvious. But in general, the task is not difficult. In the commercial version, it was possible to take a larger number of factors and, accordingly, a much larger number, then the decomposition would take more time. We figured out the factors, now let's look at the half-byte selection map at different iterations.
As you might have noticed, 4 columns are highlighted - they intersect in a pair of checks, which means that these values need to be generated separately, and they should be all different. The remaining half-bytes can be selected randomly, with the condition that for each check there will be all 4 different factors.
At the same time, I noticed some symmetry, which allows us to generate not all, but only half of the values, and fill the rest with mirror reflection.
I’ll give a small example for my nickname.
The hash from it will be equal
KEY1 and KEY2 select for example
Then to get block1-block4 you need to perform the following operations:
The fifth key block is the lower part of the hash. In my case - 622F. Well, in the last, sixth block, we have more options for choice - the general formula will be (c << 8) | (c ^ 0x5B). In the simplest case, 005B (00 ^ 5B = 5B).
The final key will be like this
If everything is found correctly, then the following window should be displayed.
My version of the key generator can be found here
This is me again, and again brings the topics of reverse engineering to the masses. Since, for some reason, I can’t cover the analysis of commercial protectors or programs in my articles, so for today our experimental rabbit will be the keygenme from TPoDT group. Not to say that it’s difficult, but it was not a pity to spend a couple of hours on it.
For those who are not in the know: keygenme is a type of program that is created by some crackers to analyze them by others. As a rule, the goal is to show some interesting mathematical algorithm or unusual code protection.
You can download keygenme here. It is worth paying tribute to the authors - keygenme is not packed in any way, which saves us from unnecessary gestures. And apparently the authors even bothered to make a nice interface.

We load it into the debugger, and set breakpoints on the standard WinAPI functions used to get the text from the input fields: We
GetDlgItem, GetDlgItemTextA, GetWindowTextA.release the program for execution, drive in any name, key and press the 'Check' button. There are no unpleasant surprises, and we immediately stop at
GetDlgItemTextA. We remove the breaks and exit the API - we are at the address 0x0040195B. 
As you can see, the text is being read from the input fields, and if they are empty, then the MessageBox with errors is displayed. Below you can see the entrance to the function
CheckCodewhich returns 0 or 1 depending on the result of the check. And accordingly, below the MessageBox pair of true and false verification options. It is worth noting that, despite the absurdity of such protection, it is found in almost half of the applications. And if the goal is simply to get a working application, not a key, then you can replace call with a sequencexor al, al inc al
But we are interested in the algorithm itself, and therefore we go into
CheckCode. 
The code is pretty clean and easy to read. The first step is to call a subprocedure called by me
GetOnlyNumeric, it is passed, as a parameter, a pointer to the entered code. 
For C enthusiasts, I specifically made comments on a C-like pseudo-code. The code in the loop reads the entered line and if the character does not lie in the range
'A'-'F'or '0'-'9', then skips the character. If the character satisfies the condition, then glues it with a new line. This is done so that you can enter the key in a "beautiful" form, with delimiters. Let's go back to the function code
CheckCode. At the address, 0x00401457you can see the count of the length of the normalized string, and it should be 24. (I have a typo in the screenshot). Why 24? REP SCASBsearches for a character from in the string AL, while decreasing ECX. Initially, ECX indicates 0xFFFFFFFF as the maximum value. Usually after that they execute commands NOT ECXand DEC ECX, in order to get the length of the string in the normal form. We will do it too-1Ah = FFFFFFE6h not FFFFFFE6hh = 19h 19h - 1 = 24dec
Subsequent function calls
sscanftranslate the normalized string into three binary DWORDs in a row. And at the very bottom of the screenshot there is a small loop that counts the hash from the entered name by XORten consecutive DWORDs of the buffer. (Buffer 40 characters long) This is where the initial preparations are completed and checks begin. 
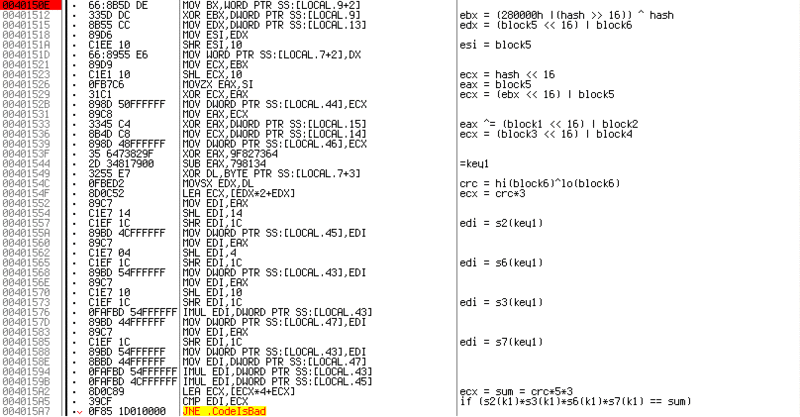
Personally, when researching programs, I first look superficially at what she does, tracing the code, and then I analyze the necessary sections in the opposite direction from the checks.
In this case, the decision will be correct at which
EDI=ECX Let's start with
ECX- right before the comparison, the command is executed LEA ECX, [ECX*4+ECX] In general,
LEAthis is a command to count the address, but in this case it executes the expression:ECX = ECX*4 + ECX ECX*5. We go up the code, ECX now occurs at the address 0x0040154F LEA ECX, [EDX*2+EDX] ECX = EDX*3*5 EDX? If you tamper with the code, then we understand that it is equal to the operation XORbetween the high and low parts of the last key block. In the future, I will call the resulting number SUM, and the infringed two bytes of the last block will be called CRC. Let me explain why a block is - after translating the entered string into a binary form, all operations on them are performed either with DWORD or WORD values. Therefore, the key type can be as follows:1111-2222-3333-4444-5555-6666
This is my variation; hyphens can also be arranged differently.
So, we learned the right part of the condition, now let's move on to the left - to calculate EDI.
I will describe briefly what happens after
SUB EAX, 798134 ECX. The first thing that comes to mind is to calculate values at which crc and KEY1 would equal 0. It seems that everything is fine, but it would be too simple, with this option all the checks are passed except the last one. But more on that later. Now let's see what happens to
EDXbefore it becomes KEY1. From the comments you can understand that at first it is considered from the lower part of the hash on behalf of the blocks and blocks block1 and block2, again using XOR. Then two operations are performed.XOR EAX, 9F827364 SUB EAX, 798134
which, to obtain the original number from KEY1, can be reversed as follows:
ADD EAX, 798134 XOR EAX, 9F827364
At this stage, we will not try to substitute numbers; first, we will look at the rest of the checks.

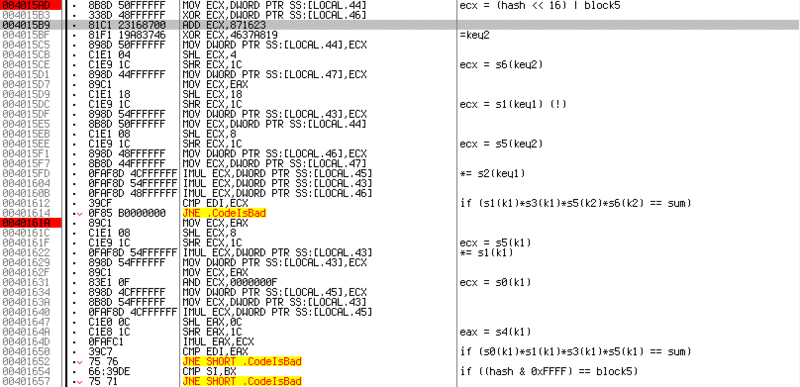
There are three of them at once in this screenshot. The first almost repeats the previous one. Of the differences, we can distinguish a change in the calculation algorithm KEY2
ADD ECX, 871623 XOR ECX, 4637A819
Which are also easily converted to
XOR ECX, 4637A819 SUB ECX, 871623
And also, the half-byte indexes have changed. Now 5 and 6 are taken from KEY2 and (!) 1, 2 from KEY1. That's why I said that it’s not worth picking up numbers, since they are still used further according to the algorithm. In further checks, key numbers are no longer generated, but two received KEY1 and KEY2 are used.
The third check multiplies 0,1,4 and 5 half-bytes of KEY1.
At the very bottom of the screenshot, at the address
0x00401654, there is a very small check CMP SI, BX. It is not complicated, and again, by means of the trace, you can see that the lower part of the hash on behalf is compared with the fifth block of the entered code. The remaining three checks are also small:
The first two of them are of the same type, and simply choose their half-bytes from the key numbers for multiplication. Therefore, I will not repeat myself. The verification located at the address deserves more attention
0x004016BF. Here she is the most insidious - she compares crc, or more simply, the pokorsennye bytes of the last block, on which all previous checks depend. And which actually does not allow us to make KEY1 and KEY2 zero. The team
SHL EDX, 1makes a shift by 1 bit to the left, which is equivalent to multiplying the number by 2. In total, we get that the index is a constant for any code and should be 0xB6 / 2 = 0x5B.Now a little math. At the very beginning, we saw that the number with which the comparison is made in the checks is CRC * 15. And since we found above that CRC = 0x5B, it is not difficult to obtain SUM = CRC * 15 = 0x555 = 1365 (10).
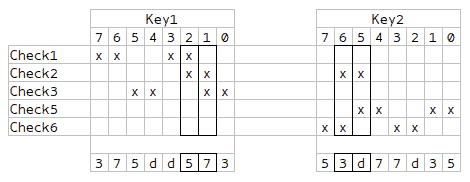
In each check, when multiplying half-bytes, 4 operands are always used, which means that we must factor 1365 into 4 factors. If the divisibility of 3 and 5 is visible by eye, then the remaining 7 and 13 are no longer so obvious. But in general, the task is not difficult. In the commercial version, it was possible to take a larger number of factors and, accordingly, a much larger number, then the decomposition would take more time. We figured out the factors, now let's look at the half-byte selection map at different iterations.

As you might have noticed, 4 columns are highlighted - they intersect in a pair of checks, which means that these values need to be generated separately, and they should be all different. The remaining half-bytes can be selected randomly, with the condition that for each check there will be all 4 different factors.
At the same time, I noticed some symmetry, which allows us to generate not all, but only half of the values, and fill the rest with mirror reflection.
I’ll give a small example for my nickname.
The hash from it will be equal
0x6930622F. The older part is not involved in the algorithm. KEY1 and KEY2 select for example
5d7337d5 d537735d. Then to get block1-block4 you need to perform the following operations:
(5d7337d5 + 798134) ^ 9F827364 = C26ECA6D block1 = C26E ^ 622F = A041 block2 = CA6D ^ 622F = A842 (d537735d ^ 4637A819) - 871623 = 9279C521 block3 = 9279 ^ 622F = F056 block4 = C521 ^ 622F = A70E
The fifth key block is the lower part of the hash. In my case - 622F. Well, in the last, sixth block, we have more options for choice - the general formula will be (c << 8) | (c ^ 0x5B). In the simplest case, 005B (00 ^ 5B = 5B).
The final key will be like this
A041-A842-F056-A70E-622F-005B
If everything is found correctly, then the following window should be displayed.

My version of the key generator can be found here
