LogLog - find the number of unique elements
Hello, Habr! You and I have already indulged in the Bloom and MinHash filters . Today we’ll talk about another probabilistic-randomized algorithm that allows you to determine the approximate number of unique elements in large amounts of data with minimal memory costs.
To begin with, let us set ourselves the task: suppose that we have a large amount of textual data - say, the fruits of the literary work of the notorious Shakespeare, and we need to calculate the number of different words found in this volume. A typical solution is a counter with a truncated hash table, where the keys are words without the values associated with them.
The way is good for everyone, but it requires a relatively large amount of memory for its work, but as you know, we are restless geniuses of efficiency. Why a lot, if not enough - the approximate size of the vocabulary of Shakespeare mentioned above can be calculated using only 128 bytes of memory.
As usual, we need some kind of hash function; accordingly, not the data itself, but their hashes will come to the input of the algorithm. The task of the hash function, as is usually the case in randomized algorithms, is to turn ordered data into “random” data, that is, in a more or less uniform spread of the definition domain over the range of values. For the test implementation, I chose FNV-1a as a nice and simple hash function:
Well, turn on the brain and look at the hashes that it gives in binary representation: Pay attention to the index of the first nonzero low-order bit for each hash, add one to this index and call it rank (rank (1) = 1, rank (10 ) = 2, ...):
The probability that we will have a hash with a rank of 1 is 0.5, with a rank of 2 - 0.25, and with a rank of r - 2 - r . In other words, among 2 r hashes, one hash of rank r must meet . In other words, if we remember the largest R rank detected , then 2 R will fit in as a rough estimate of the number of unique elements among those already viewed.
Well, the probability theory is such that we can find a large rank R in a small sample, but we can also small in an enormous sample, and in general 2 31 and 2 32- these are two big differences, you say, and you will be right, which is why such a single assessment is very rough. What to do?
Instead of one hash function, you can use a bundle of these, and then somehow “average” the estimates obtained for each of them. This approach is bad because we need a lot of functions and all of them have to be considered. Therefore, we will do the following trick - we will gnaw off the k most significant bits from each of the hashes and, using the value of these bits as an index, we will calculate not one estimate, but an array of 2 k ratings, and then based on them we will get the integral one.
In fact, there are several variations of the LogLog algorithm, we will consider a relatively recent option - HyperLogLog. This version allows you to achieve the standard error:
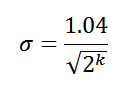
Therefore, when using the 8 high-order bits as an index, we get a standard error of 6.5% ( σ = 0.065) of the true number of unique elements. And most importantly, if you arm yourself with mad skills based on probability theory, you can come to the following final estimate:
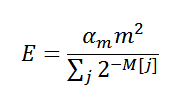
where α m is the correction coefficient, m is the total number of ratings (2 k ), M is the array of the ratings themselves. Now we know almost everything, it's time for implementation :
Let's estimate how many bytes of memory we use, k is 8, therefore, the array M consists of 256 elements, each of them, by convention, takes 4 bytes, which in total is 1 KB. Not bad, but I would like less. If you think about it, the size of a single estimate from the array M can be reduced - you just need ceil (log2 (32 + 1 - k )) bits, which, for k = 8, is 5 bits. In total, we have 160 bytes, which is already much better, but I promised even less.
In order to be less, it is necessary to know in advance the maximum possible number of unique elements in our data - N. Indeed, if we know it, there is no need to use all possible bits from the hash to determine the rank, ceil (log2 ( N / m )) bits are enough . Do not forget that from this number, we again need to take the logarithm, to get the size of a single element of the array M .
Suppose that, in the case of our small set of words, their maximum number is 3,000, then we need only 64 bytes. In the case of Shakespeare, we put N equal to 100,000, and we will have the promised 128 bytes with an error of 6.5%, 192 bytes at 4.6%, 768 at 3.3%. By the way, the real size of Shakespeare's vocabulary is about 30,000 words.
Of course, using small "bytes", for example, 3 bits each is not very efficient in terms of performance. In practice, it’s better not to go crazy building quite long chains of bit operations, but to use the usual bytes native to the architecture. If you still decide to "grind", do not forget to correct the code correcting the assessment.
A small fly in the ointment, the error σ is not the maximum error, but the so-called standard error. For us, this means that 65% of the results will have an error of no more than σ , 95% - no more than 2 σ and 99% - no more than 3 σ . It is quite acceptable, but there is always a chance to get an answer with an error greater than expected.
Judging by my experiments, one should not get too carried away with its reduction, especially if little data is expected. In this case, the correction procedure begins, which does not always cope with its responsibilities. It seems that the algorithm requires testing and tuning for a specific task, unless, of course, this is some stupid mistake in my implementation. This is not entirely true .
When using a hash function with a width of 32 bits, the algorithm allows you to calculate up to 10 9 unique elements with a minimum achievable standard error of about 0.5%. Memory, with such an error, you need about 32-64 Kbytes. In general, LogLog is ideal for on-line work with live data streams.
That's all. Till!
To begin with, let us set ourselves the task: suppose that we have a large amount of textual data - say, the fruits of the literary work of the notorious Shakespeare, and we need to calculate the number of different words found in this volume. A typical solution is a counter with a truncated hash table, where the keys are words without the values associated with them.
The way is good for everyone, but it requires a relatively large amount of memory for its work, but as you know, we are restless geniuses of efficiency. Why a lot, if not enough - the approximate size of the vocabulary of Shakespeare mentioned above can be calculated using only 128 bytes of memory.
Idea
As usual, we need some kind of hash function; accordingly, not the data itself, but their hashes will come to the input of the algorithm. The task of the hash function, as is usually the case in randomized algorithms, is to turn ordered data into “random” data, that is, in a more or less uniform spread of the definition domain over the range of values. For the test implementation, I chose FNV-1a as a nice and simple hash function:
function fnv1a(text)
{
var hash = 2166136261;
for (var i = 0; i < text.length; ++i)
{
hash ^= text.charCodeAt(i);
hash += (hash << 1) + (hash << 4) + (hash << 7) + (hash << 8) + (hash << 24);
}
return hash >>> 0;
}Well, turn on the brain and look at the hashes that it gives in binary representation: Pay attention to the index of the first nonzero low-order bit for each hash, add one to this index and call it rank (rank (1) = 1, rank (10 ) = 2, ...):
fnv1a('aardvark') = 10011000000000011101001000110011
fnv1a('abyssinian') = 00101111000100001010001000111100
fnv1a('accelerator') = 10111011100010100010110001010100
fnv1a('accordion') = 01110101110001001110100000011001
fnv1a('account') = 00101001010011111100011101011100
fnv1a('accountant') = 00101010011011111100111100101101
fnv1a('acknowledgment') = 00001010000100111000001111101000
fnv1a('acoustic') = 11110011101011111110010101100010
fnv1a('acrylic') = 11010010011100110111010111011000
fnv1a('act') = 00101101010010100100010110001011function rank(hash)
{
var r = 1;
while ((hash & 1) == 0 && r <= 32) { ++r; hash >>>= 1; }
return r;
}The probability that we will have a hash with a rank of 1 is 0.5, with a rank of 2 - 0.25, and with a rank of r - 2 - r . In other words, among 2 r hashes, one hash of rank r must meet . In other words, if we remember the largest R rank detected , then 2 R will fit in as a rough estimate of the number of unique elements among those already viewed.
Well, the probability theory is such that we can find a large rank R in a small sample, but we can also small in an enormous sample, and in general 2 31 and 2 32- these are two big differences, you say, and you will be right, which is why such a single assessment is very rough. What to do?
Instead of one hash function, you can use a bundle of these, and then somehow “average” the estimates obtained for each of them. This approach is bad because we need a lot of functions and all of them have to be considered. Therefore, we will do the following trick - we will gnaw off the k most significant bits from each of the hashes and, using the value of these bits as an index, we will calculate not one estimate, but an array of 2 k ratings, and then based on them we will get the integral one.
HyperLogLog
In fact, there are several variations of the LogLog algorithm, we will consider a relatively recent option - HyperLogLog. This version allows you to achieve the standard error:
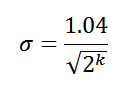
Therefore, when using the 8 high-order bits as an index, we get a standard error of 6.5% ( σ = 0.065) of the true number of unique elements. And most importantly, if you arm yourself with mad skills based on probability theory, you can come to the following final estimate:
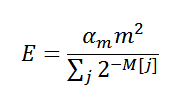
where α m is the correction coefficient, m is the total number of ratings (2 k ), M is the array of the ratings themselves. Now we know almost everything, it's time for implementation :
var pow_2_32 = 0xFFFFFFFF + 1;
function HyperLogLog(std_error)
{
function log2(x)
{
return Math.log(x) / Math.LN2;
}
function rank(hash, max)
{
var r = 1;
while ((hash & 1) == 0 && r <= max) { ++r; hash >>>= 1; }
return r;
}
var m = 1.04 / std_error;
var k = Math.ceil(log2(m * m)), k_comp = 32 - k;
m = Math.pow(2, k);
var alpha_m = m == 16 ? 0.673
: m == 32 ? 0.697
: m == 64 ? 0.709
: 0.7213 / (1 + 1.079 / m);
var M = []; for (var i = 0; i < m; ++i) M[i] = 0;
function count(hash)
{
if (hash !== undefined)
{
var j = hash >>> k_comp;
M[j] = Math.max(M[j], rank(hash, k_comp));
}
else
{
var c = 0.0; for (var i = 0; i < m; ++i) c += 1 / Math.pow(2, M[i]);
var E = alpha_m * m * m / c;
// -- make corrections
if (E <= 5/2 * m)
{
var V = 0; for (var i = 0; i < m; ++i) if (M[i] == 0) ++V;
if (V > 0) E = m * Math.log(m / V);
}
else if (E > 1/30 * pow_2_32) E = -pow_2_32 * Math.log(1 - E / pow_2_32);
// --
return E;
}
}
return {count: count};
}
function fnv1a(text)
{
var hash = 2166136261;
for (var i = 0; i < text.length; ++i)
{
hash ^= text.charCodeAt(i);
hash += (hash << 1) + (hash << 4) + (hash << 7) + (hash << 8) + (hash << 24);
}
return hash >>> 0;
}
var words = ['aardvark', 'abyssinian', ..., 'zoology']; // 2 336 words
var seed = Math.floor(Math.random() * pow_2_32); // make more fun
var log_log = HyperLogLog(0.065);
for (var i = 0; i < words.length; ++i) log_log.count(fnv1a(words[i]) ^ seed);
var count = log_log.count();
alert(count + ', error ' + (count - words.length) / (words.length / 100.0) + '%');Let's estimate how many bytes of memory we use, k is 8, therefore, the array M consists of 256 elements, each of them, by convention, takes 4 bytes, which in total is 1 KB. Not bad, but I would like less. If you think about it, the size of a single estimate from the array M can be reduced - you just need ceil (log2 (32 + 1 - k )) bits, which, for k = 8, is 5 bits. In total, we have 160 bytes, which is already much better, but I promised even less.
In order to be less, it is necessary to know in advance the maximum possible number of unique elements in our data - N. Indeed, if we know it, there is no need to use all possible bits from the hash to determine the rank, ceil (log2 ( N / m )) bits are enough . Do not forget that from this number, we again need to take the logarithm, to get the size of a single element of the array M .
Suppose that, in the case of our small set of words, their maximum number is 3,000, then we need only 64 bytes. In the case of Shakespeare, we put N equal to 100,000, and we will have the promised 128 bytes with an error of 6.5%, 192 bytes at 4.6%, 768 at 3.3%. By the way, the real size of Shakespeare's vocabulary is about 30,000 words.
Other thoughts
Of course, using small "bytes", for example, 3 bits each is not very efficient in terms of performance. In practice, it’s better not to go crazy building quite long chains of bit operations, but to use the usual bytes native to the architecture. If you still decide to "grind", do not forget to correct the code correcting the assessment.
A small fly in the ointment, the error σ is not the maximum error, but the so-called standard error. For us, this means that 65% of the results will have an error of no more than σ , 95% - no more than 2 σ and 99% - no more than 3 σ . It is quite acceptable, but there is always a chance to get an answer with an error greater than expected.
When using a hash function with a width of 32 bits, the algorithm allows you to calculate up to 10 9 unique elements with a minimum achievable standard error of about 0.5%. Memory, with such an error, you need about 32-64 Kbytes. In general, LogLog is ideal for on-line work with live data streams.
That's all. Till!
