What tasks are well suited for research?
- Transfer

What number should be inserted in the last triangle?
Scientists solve problems; such is their job. But what tasks will be promising research topics? To answer this question, I wrote the book Lost in Mathematics , where I considered problems related to the fundamentals of physics.
The first, rough classification of research problems can be organized using the development cycle of the scientific theories of Thomas Kuhn. The Kuhn cycle consists of a phase of “ordinary science”, followed by a “crisis” leading to a paradigm shift, after which a new phase of “ordinary science” begins. This is an incredible simplification of reality, but is suitable for subsequent reasoning.
Common tasks
During the normal science phase, research questions can usually be formulated as “How would we measure it?” (For experimenters) and “How would we calculate this?” (For theoreticians).
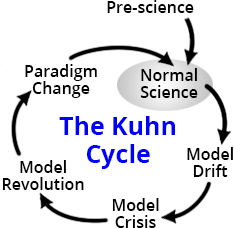
In the fundamentals of physics, such “ordinary problems” are complete. Experimenters have many problems, because all easily solved tasks have already been solved, and the complexity of measuring something new is constantly growing. Problems with theorists come from the fact that predictions in physics do not fall out of hypotheses by themselves. It is often required to go through many stages of argumentation and do a lot of lengthy calculations in order to arrive at numerical consequences of theoretical assumptions.
A good example of a common problem in the fundamentals of physics would be cold dark matter. The hypothesis is quite simple: in space there is a cold and dark something that behaves like a liquid and interacts weakly with itself and with other matter. But this in itself is not a particularly useful prediction. A good research task would be the following: “How does cold dark matter affect the temperature fluctuations of the CMB radiation?” And then comes the experimental question: “How do we measure it?”
Other tasks of this type in the fundamentals of physics are: “How does gravity contribute to magnetic muon moment? ”and“ What is the background of photon scattering in the Large Hadron Collider? ”
Answers to such ordinary tasks broaden our understanding of existing theories. These calculations can be done within the framework of our existing platforms, but they can be quite complex.
The problems given in the previous paragraphs as examples are solved, or at least we know how to solve them, although you can always request improvements in accuracy. But in this category there are unresolved problems.
For example, the quantum theory of strong nuclear interaction should predict the masses of particles consisting of several quarks — neutrons, protons, and other similar (but unstable) composite particles. But such calculations are damn complicated. Today, they are carried out with the help of sophisticated computer programs — lattice calculations — and still their predictions are not so good. A related question is how nuclear matter behaves in the nuclei of neutron stars.
These are simply randomly selected examples of many open-ended questions of physics, which are “normal problems” to which, it is believed, can be answered within the framework of theories we already know - but I think they illustrate this topic well.
If you go beyond the basics, then we have normal tasks like predicting solar cycles and sunny weather — they are complicated due to extreme non-linearity and partial turbulence of the system, but we do not expect them to conflict with existing theories. There is also high-temperature superconductivity, a well-studied, but theoretically insufficiently understandable phenomenon, since such materials lack quasiparticles. And so on.
We study such tasks when everything goes according to plan. But there are still tasks that, in principle, can change paradigms, tasks reporting the existence of a “crisis” in Kuhn's terminology.
Crisis challenges
Obvious crisis tasks are observations that cannot be explained on the basis of known theories.
I do not consider most of the observations related to dark matter and dark energy to be crisis. Most of this data can be explained quite well by simply adding two new components to the energy budget of the Universe. Of course, you will complain that this will not give us a microscopic description, but we don’t have data for microscopic structures, so it’s impossible to formulate the task yet.
But some dark matter observations refer to the "crisis". Unexplained correlations, patterns in galaxies that are difficult to explain with the help of cold dark matter, for example, the dependence of Tally - Fisheror the strange ability of dark matter to track the distribution of matter. For these observations, there is no satisfactory explanation based on known theories. Gravity modification successfully explains some of them, but causes other problems. So much for the crisis! And this is a good crisis, I dare say, because we have data that is improving every day.
This is not the only good crisis problem of observation that exists in the fundamentals of physics. One of the oldest, but still alive and well, is the magnetic moment of the muon . We have a long-standing discrepancy between theoretical predictions and measurements, which has not yet been resolved. Many theorists consider this to be a sign that it cannot be explained in the framework of the Standard Model, and therefore a new, improved theory is required.
There are a couple of similar problems, and quite stubborn. For example, the DAMA experiment . In this experiment, scientists are looking for dark matter. They receive a signal from an unknown source with an annual modulation, and have been watching it for more than ten years. The signal is exactly there, but if it turns out to be dark matter, the result will conflict with other experimental results. In the end, DAMA sees something, but no one knows what it is.
There are also puzzling observations of the LSND experiment on neutrino oscillations that are not consistent with any other combination of parameters. There is also a strange discrepancy in the results of measurements of the proton radius using two different methods, as well as another similar story with the neutron lifetime. Also recently, there have been contradictions in the measurement of the Hubble parameter using different methods, and this may not be worth it, and perhaps that should be worried.
Of course, each of these anomalies in the data may have a “usual” explanation. This may be a systematic measurement error or a calculation error or a missing ingredient contributing. But perhaps, perhaps, this is something more.
This is one of the types of "crisis problems" - the conflict between theory and observation. But besides these, there are crisis problems of a completely different kind, located on the side of developing theories. These are problems of internal consistency.
The problem of internal consistency arises when your theory predicts conflicting, ambiguous or meaningless observations. A typical example of this is probabilities that become greater than one, which does not coincide with the interpretation of probability. It was because of this problem that physicists were confident that the LHC would show us the new physics. They did not know whether it would be a Higgs, and it could have been something else — for example, an unexpected change in weak nuclear interaction — but it turned out to be Higgs. The restoration of internal consistency led to a successful prediction.
Historically, the study of problems with consistency has led to many striking breakthroughs.
An example of such a problem can serve as " ultraviolet catastrophe", in which the heat source would emit an infinite amount of light at small wavelengths. This clearly does not correspond to a meaningful physical theory, in which the observed values must be finite. (Note that this conflict arises with an assumption. Mathematically there is nothing bad in infinity Planck solved this problem, and the solution eventually led to the development of quantum mechanics.
Another well-known problem with consistency is related to the fact that Newtonian mechanics turned out to be incompatible with the symmetry of space-time electrodynamics. Einstein resolved this disagreement and received a special theory of relativity. Dirac later resolved the contradiction between quantum mechanics and the STR, which led to the creation of quantum field theory. Einstein eliminated additional contradictions between the STR and the Newtonian gravity, and obtained GRT.
All these problems were well defined and specified.
But most of today's theoretical problems in the fundamentals of physics do not belong to this type. Yes, it would be nice if the three interactions of the Standard Model could be combined into one. It would be nice, but it is not necessary for consistency. Yes, it would be nice if the Universe was supersymmetric. It would be nice, but it is not necessary for consistency. Yes, it would be nice if we could explain why the Higgs mass is technically unnatural. But there is no contradiction in the fact that the Higgs mass is as it is.
Well described is the fact that Einstein, and even more Dirac, was inspired by the beauty of his theories. Dirac especially liked to praise the use of mathematical elegance in developing theories. But their personal motivation interests us insofar as. Looking back, we understand that they have achieved success, because initially they took on good tasks.
In the fundamentals of physics today there are few real theoretical problems, but they exist. One of them is the lack of quantization of gravity. Mathematically, it is impossible to simply rake the Standard Model and GTR in one pile, and we do not know how to do it correctly.
Another serious problem with the Standard Model is the Landau pole in one of the coupling constants.. This means that the strength of one of the interactions becomes infinite. This is not a physical result, just like an ultraviolet disaster, so something must happen here. Little attention has been devoted to this problem, since most theorists believe that the standard model is combined long before reaching the Landau pole, which is why extrapolation becomes redundant.
There are still cases in which it is not clear what kind of task we are dealing with. One of them is the divergence of expansion in small perturbations [non-convergence of the perturbative expansion]. Perhaps the only question is to improve the mathematical apparatus, or perhaps we quite misunderstand quantum field theory. The same case with the Haag theorem . I also find it difficult to classify the measurement problem.in quantum mechanics. An appeal to macroscopic processes in the axioms of the theory is incompatible with the ideals of reductionists, but, again, this is not a fundamental problem, but a conceptual concern. So what about this issue I am in difficulty.
However, the lesson that the history of crisis problems teaches us is clear: problems are promising research topics if they really represent problems. That is, you should be able to formulate a mathematical contradiction. If the problem is simply that you do not like a certain aspect of the theory, then you will most likely just spend your time.
