Conservative logic
Overclockers armed with liquid nitrogen have repeatedly shown that modern chips can work stably at frequencies several times higher than the nominal ones, providing a corresponding increase in performance. Nevertheless, progress in the field of “gigahertz race” has stopped long ago and reliably. The first Pentium 4 with a frequency of more than 3 GHz appeared back in 2002, almost 10 years ago. Over the past years, the norms of technical processes have decreased from 180 to 32 nm, but even this did not significantly raise the standard operating frequencies. Everything rests on the huge heat emission of the elements of digital logic.
The “heat release problem” is based on a deep connection between informational and thermodynamic entropy, as well as the second law of thermodynamics, which prohibits a decrease in the total entropy of a closed system. Any calculation that reduces the informational entropy must lead to an increase in the thermodynamic entropy, that is, to the generation of heat. Rolf Landauer in 1961 showed [ pdf ] that the destruction of one bit of information should lead to the release of at least k ∙ T ∙ ln 2 joules of energy, where k is the Boltzmann constant and T is the temperature of the system. This energy itself is small: for T = 300K it is only 0.017 eV per bit, but in terms of the processor as a whole, the total energy rises to values of the order of one Joule for every second of operation, that is, of the order of one Watt [ Computerra No. 538]. In practice, this theoretical minimum is multiplied by non-zero resistance and other non-ideals of real semiconductors. As a result, we get processors that outperform irons in terms of heat.
The destruction of information in modern processors occurs constantly and at the lowest level, in the "NAND" gates, which are the "bricks" of any modern digital circuit. Taking two bits as an input, the valve produces a result of just one bit, from which, of course, you cannot restore the values of the original arguments. More strictly, each calculation by the NAND gate reduces informational entropy by 1.189 bits, and, accordingly, dissipates at least ~ 0.02 eV of heat. With the unpopular OR-NOT today, the situation is similar.
Things are not better with memory cells, any entry in which leads to the destruction of previous values. For a programmer, old data is simply “lost”, but laws of conservation of charge and energy do not allow them to get lost “just like that” on a physical level. In fact, old information is not destroyed, it is scattered in space in the form of heat and spurious radiation.
For more than 30 years, a method of organizing calculations without destroying information has been known, which does not fall under the Landauer principle and allows the creation of theoretically energy-efficient processors. This method is called conservative, or "preserving", logic. Unfortunately, it was not possible for him to create a compact physical implementation in silicon, only the method of implementation on MOS transistors with poorly miniaturized inductors is known. On the other hand, this approach is natural for most types of quantum computers, including optical ones (Benioff’s model, etc.)
Over the years, it turned out that conservative logic turned out to be a useful mathematical abstraction without implementation "in hardware": block cellular automata are created on its basis, which are very convenient to use when solving problems "for limited resources." This branch of mathematics is now very actively developing, and, perhaps, in a decade or so, block cellular automata will be even more famous among programmers than ordinary ones.
The “butterfly wing flap” that led to the appearance of this article was the question raised by Comrade Plakhov, “How is it in Russian?”, The answer to which even Yandex does not know. In addition to the 2004 article in Computerra mentioned above, there is no information on conservative logic in Russian at all - all the more offensive, since its theoretical foundations were laid down by the great Soviet physicists Landau and Lifshits exactly 50 years ago, in 1961. In order to at least slightly eliminate this gap, on the one hand, and not “smack the gag,” on the other, I bring to your attention an abstract (translation of the main points) of a fundamental article on the conservative logic of Eduard Fredkin and Tomasso Toffoli published in the journal Theoretical Physics No. 21 for 1982. (Fredkin, Edward and Toffoli, Tomasso, “Conservative Logic”, Int. J. Theor. Phys. 21 (1982), 219–253;pdf ). This article reveals all the main points regarding the physics, logic, and circuitry of systems based on conservative logic.
Conservative or conservation logic is a mathematical model of the organization of calculations based on two fundamental physical principles: reversibility of processes and conservation laws.
(The numbering of sections of the abstract does not coincide with the numbering of parts of the article - approx. Per. )
Any calculation, no matter how it is performed, by a person or by a machine, must obey certain physical laws. In particular, the speed of information dissemination is limited by the speed of light, and the amount of information in the final system must also be finite. There are more complex limitations.
All physical laws can be divided into dynamic and statistical. The former describe the behavior of individual objects in fully defined microscopic systems and allow, in classical mechanics, to accurately predict the outcome of any experiment. When there are too many objects to calculate each of them, statistical laws are applied that describe the average behavior of homogeneous objects in the macro system. They allow you to evaluate the picture as a whole, but do not provide an opportunity to predict the behavior of a particular object.
At the micro level, our world has various fundamental homogeneities and symmetries, many of which lead to the emergence of "conservation laws" at the macro level. Thus, the uniformity of time ensures the fulfillment of the law of conservation of energy, the uniformity of space - the law of conservation of momentum, and the isotropy of space (symmetry of directions) leads to the conservation of the moment of rotation.
All dynamic fundamental physical laws are reversible in the sense of replacing coordinates by inverse ones. You can reverse the beat in billiards if you let all the balls go in the strictly opposite direction. On the other hand, statistical physical laws obey the principles of thermodynamics and are not reversible without reversing the arrow of time; a broken vase will never be assembled from fragments. In particular, the traditional computational model operating at the macro level is based on the AND-NOT or OR-NOT gates. Any calculation in such a model requires energy costs in accordance with the Landauer principle.
In any organization of computations, digital information physically represents the numbered stable states of any systems.
Although in fact these states can be electrical, optical, etc., hereinafter we will call them “mechanical” to distinguish them from thermodynamic states. Thermodynamic states are degrees of freedom of individual atoms and molecules that make up a substance. In one gram of any substance there is a huge, about 10 23 (Avogadro number), the number of such degrees of freedom, and they can be taken into account only by statistical methods and laws.
The second law of thermodynamics says that the total entropy of a closed system cannot decrease. The Landauer principle establishes the energy relationship between informational and thermodynamic entropy. Many algorithms lead to a decrease in information entropy, but such a decrease should either be compensated by an increase in thermodynamic entropy (heat generation), or it should be prohibited.
Accordingly, two fundamentally different approaches to the physical organization of calculations are possible.
With a “conservative” or “preserving” approach for storing information, mechanical conditions are selected for which the entropy exchange with thermodynamic states is impossible. In such a system, any operations that reduce information entropy, in particular, information destruction operations, should be prohibited. Therefore, all operations must be reversible. Landau and Livshits showed that in such a system there must exist some invariant additive quantities, for example, charges or moments “protected” by the conservation law - only then will the transition of “charges” to “temperature” and vice versa be impossible. The total level of these quantities available in a closed system will be constant and independent of the processes occurring in the system.
Unlike the conservative one, with the usual “von Neumannian” approach, calculations are initially irreversible. To satisfy the second law of thermodynamics, there must exist a path for the exchange of entropy and energy between the mechanical and thermodynamic degrees of freedom. Such a path should be one-sided (i.e. irreversible) so that thermal fluctuations cannot destroy the information stored in mechanical states. But, since at the micro level all processes are reversible, it is possible to achieve a one-sided flow of entropy only if the energy difference between the mechanical states is much orders of magnitude greater than between the thermodynamic ones. In modern computer technology (1982 - approx. Trans. ) The difference is from 8 to 12 orders of magnitude.
All of today's computing technology is built on a second, "irreversible" path. Irreversibility is specially laid down in the basic logic circuits, in pn junctions of transistors, and even if the calculated high-level algorithm is formally reversible - when executed on modern processors, at least part of its individual steps is irreversible at the lowest level. Irreversibility also means high heat dissipation, which limits achievable performance.
Computational models based on the conservative principle should use basic logic elements that satisfy certain conditions. In particular, they must be reversible and preserve the very additive quantities (charges, moments). From the second requirement it follows that the number of inputs of an element must be equal to the number of outputs, which, in turn, means a functional composition strictly “one to one”.
Conservative logic is based on two elements - the repeater and the Fredkin gate.
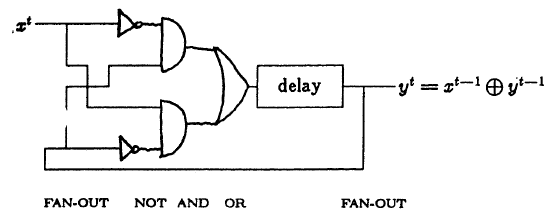
The repeater (unit wire; literally "elementary conductor") simply repeats the output signal fed to its input, with a delay of 1 clock cycle. It is the speed of the repeaters that determines the clock frequency of the circuit. Formally, the repeater function is expressed as:
y t = x t-1
Legend: The
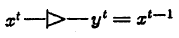
repeater can perform the functions of both storing (being closed to itself) and transmitting information inside the circuit, but its main task is to synchronize signals with a clock generator.
The element opposite to the repeater is the same repeater, but directed in the opposite direction.
The values at the outputs of the repeaters on a particular clock cycle completely describe the internal state of the digital circuit of the conservative logic, that is, the outputs of the repeaters are state variables of such a circuit. The sum of the values at the outputs of the repeaters will be that same additive stored value (“total charge”), and, for a closed system, a constant value. The total number of repeaters in the circuit can be regarded as the number of degrees of freedom of this circuit.
Repeaters are remotely similar, but far from equivalent, to delay elements in conventional “von Neumann” circuitry.
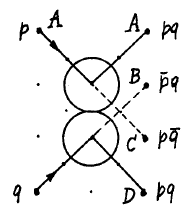
Fredkin's Gate- this is a device with three inputs u, x1, x2 and three outputs v, y1, y2, which implements the function of controlled “overlap” (“cross”) of two data lines (see. Fig.). Output v always matches input u. For u = 1, the outputs y1, y2 are equal to the inputs x1, x2; for u = 0, y1 = x2 and y2 = x1 (see table).
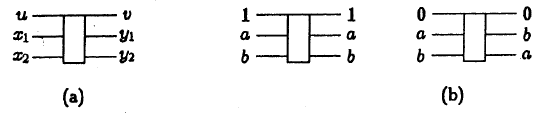
The truth table of the Fredkin gate:
(u, x1, x2) => (v, y1, y2)
0,0,0 => 0,0,0
0,0,1 => 0,1,0
0,1,0 => 0,0,1
0,1,1 => 0,1,1
1,0,0 => 1,0,0
1, 0.1 => 1,0,1
1,1,0 => 1,1,0
1,1,1 => 1,1,1
Fredkin gate is opposite to itself.
Thus, any circuit in conservative logic is a controllable conditional signal router, at the outputs of which a certain controllable rearrangement of input values at previous clock cycles is formed.
In conservative logic, it is possible to implement a Turing machine (Bennett, 1973) and a universal cellular automaton (Toffoli, 1980). Thus, conservative logic allows one to solve any Church computable problems.
The process of implementing arbitrary functions in conservative logic is very similar to the same process in traditional logic.
As in traditional circuitry, when implementing some functions, constants are used - sources of constant values 0 or 1. On the other hand, as a result of calculations, not only the required results can be obtained, but also side ones that are not needed for further use in a particular algorithm. The side effects obtained are called “garbage” or “sinks”. Since in conservative logic the signals do not appear “out of nowhere” and do not disappear “to nowhere”, it is simply impossible to discard lines with “unnecessary” results, they must be disposed of in a special way (scattered in space).
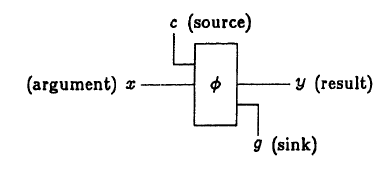
The figure shows the legend for the unit of calculation of a certain function φ:
This is how the block " I " is arranged :
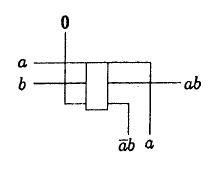
(note that one of the sinks is a copy of the argument)
The following figure shows the implementation of the logical functions " OR " (a), " NOT " (b) and the signal splitter 2a-a. The last two differ only in the logical role of the conclusions.
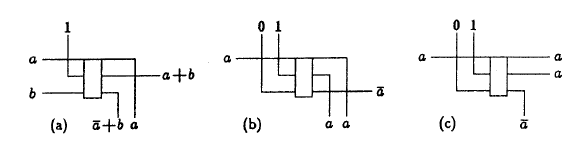
The following diagram shows a simple memory element, a JK trigger . A question mark indicates a drain that does not have any meaningful meaning.
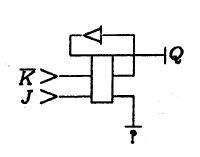
The following is a more complex scheme: a demultiplexer sending a signal X to the binary address A0, A1 to one of the four outputs Y0 - Y3:
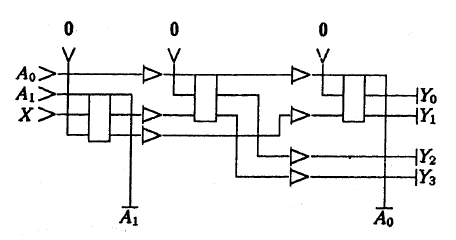
In conservative logic, any circuit from “ordinary” logic can be implemented. For example, the following three figures show the implementation of a single-bit sequential adder : the first in conventional logic (in the old notation), and the second and third in a conservative one. Moreover, the second scheme is assembled by simply substituting substitutions for the first, and the third is created “from scratch”. The difference between the repeaters and the delay elements is visible on the circuits: in conservative circuits, the signals are synchronized explicitly.


The practical value of conservative logic, if implemented, for example, in quantum computers, depends entirely on the number of drains requiring utilization in real calculations. Destruction of drains is the same “energy-generating” operation, which is also inherent in conventional circuitry. If for each trigger of the processor there will be its own drain, there will be no gain in energy release.
It is impossible to completely avoid the appearance of drains. For example, in many real-world algorithms, the final result is the sum of any numbers. But the summation operation itself is irreversible, since, knowing only its result, it is impossible to determine the initial terms. In a universal processor that executes in turn many different programs and algorithms, there will be too much such “extra” information to be simply collected. A special “entropy exchanger” will be required, into which the waste results will be delivered.
Depending on the type of function being calculated, there are three possible scenarios for the ratio of the number of necessary constants and sinks (see Fig.):

The third, best scenario is possible only if the calculated function f itself is reversible and obeys the current conservation laws.
There is a way to partially solve the drain problem, and at the same time to order the generation of constants using inverted circuits. By “inverted” is meant a circuit reversing a given one, that is, restoring inputs and constants from given outputs and drains. Since all circuits in conservative logic are reversible, for the inversion of the circuit it is enough to simply turn all the repeaters in the opposite direction and call the inputs the outputs; or, which is the same thing, reflect the scheme in the mirror (see. Fig.).
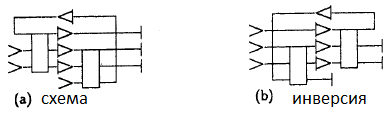
The direct and inverted circuit can be connected in series with each other. The element obtained in this way will duplicate its inputs with a long delay, without requiring any constants and without creating drains, but somewhere inside it will have the results of the calculations of the original function (see. Fig.).
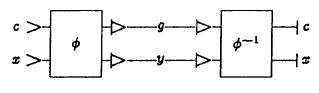
The calculated values of the original function can be "pulled out" if you "embed" spy splitters into the circuit:

To use such a circuit, you still need to provide constants (more precisely, a scratchpad register that needs to be filled in once with the required zeros and ones) , and also correctly fill in both the output and output registers. The output of such a scheme is a) a copy of the arguments, b) the result, and c) the inversion of the result, and if any of this is not used anywhere else, then they will also have to be disposed of.
The main advantage of this method is that the number of "drain" lines is proportional to only the bit depth of the input. At the same time, the number of gates needed to implement most of the real functions in any logic grows approximately as an exponent of the input bit depth. In conventional circuitry, all valves release heat, in conservative - only "drain", therefore, with a large bit depth of the inputs, the benefit should be huge.
This part presents an abstract physical model in which conservative logic is implemented.
The model is a plane along which billiard balls move without friction in strictly specified directions. The velocities, permissible directions, and sizes of the balls are selected in such a way that at discrete time instants corresponding to measures, the balls can only be in a small set of points forming a rectangular grid rotated by 45 '(see Fig.). If the balls fall into neighboring points, an elastic collision occurs between them.

The logical unit is the presence of the ball, and zero - its absence.
An arbitrary grid point can be declared a “interaction gate” if the trajectories of two balls intersect in it. The direction of exit of these balls depends on the presence of both:
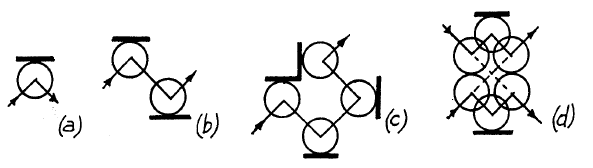
On the plane, fixed walls or mirrors can be installed. Using mirrors, you can rotate (a), shift (b), hold, and safely cross the paths (d) of the balls. The last element (d) is called a “nontrivial crossover” and allows the balls to “pass through each other”.
It is possible to create managed switches. The figure shows: a block diagram of a simple switch, the designation of the inverse switch element, as well as a diagram of the implementation of a simple switch.
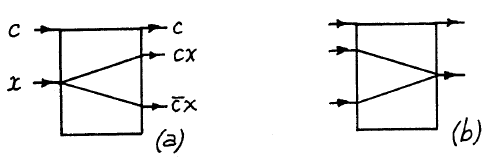

Finally, from simple switches and a non-trivial crossover (indicated by a “bridge”), you can construct a Fredkin valve (turning mirrors and delays are not shown for clarity):
As for the real physical embodiment, the molecules of gas are more suitable for the role of balls, rather than real billiard balls, although neither one nor the other option has ever been implemented.
The main advantage of the billiard balls model is its simplicity: thanks to specially selected angles and speeds, the results of all collisions can be calculated by simple Boolean functions, without the participation of floating-point numbers, costly rounding operations, etc. This allows you to quickly simulate even very large schemes of conservative logic on traditional computers.
1. Are arbitrary calculations possible in conservative logic? Yes, possible, conservative logic is Turing-complete.
2. Are there physical effects on which conservative logic can be implemented? Yes, it can be implemented on the basis of electronic elements (discrete L / R / C elements plus MOS transistors) (in practice, by 2011 everything remains only on paper and in laboratories - approx. Per. )
3. Will there be energy needed for waste disposal, more than the potential gain from switching to conservative logic? A complete answer to this question cannot be given without taking into account a specific physical model, but the method of hiding drains described in Section 4. leaves very high chances for a negative (in the sense of an optimistic) answer.
4. Finally, the question of the stability of the system to low noise is still unanswered.
The very fact that by controlledly mixing the wiring in a bundle or cable between the input and output and not using any other elements except “overlap” and repeaters, you can get the result of calculating any function from the input at the output is far from obvious. The underlying computational logic is unusual, but unlike other Turing-complete mathematical abstractions, such as Markov algorithms, it looks very “technological”, ready for use in real processors. Quite possibly, quantum computers will work on something similar, adjusted for purely quantum "tricks." If we combine conservative quantum logic with superconducting interconnects, we can build a computer that is practically practically not absorbing energy. Well, the future will show.
The “heat release problem” is based on a deep connection between informational and thermodynamic entropy, as well as the second law of thermodynamics, which prohibits a decrease in the total entropy of a closed system. Any calculation that reduces the informational entropy must lead to an increase in the thermodynamic entropy, that is, to the generation of heat. Rolf Landauer in 1961 showed [ pdf ] that the destruction of one bit of information should lead to the release of at least k ∙ T ∙ ln 2 joules of energy, where k is the Boltzmann constant and T is the temperature of the system. This energy itself is small: for T = 300K it is only 0.017 eV per bit, but in terms of the processor as a whole, the total energy rises to values of the order of one Joule for every second of operation, that is, of the order of one Watt [ Computerra No. 538]. In practice, this theoretical minimum is multiplied by non-zero resistance and other non-ideals of real semiconductors. As a result, we get processors that outperform irons in terms of heat.
The destruction of information in modern processors occurs constantly and at the lowest level, in the "NAND" gates, which are the "bricks" of any modern digital circuit. Taking two bits as an input, the valve produces a result of just one bit, from which, of course, you cannot restore the values of the original arguments. More strictly, each calculation by the NAND gate reduces informational entropy by 1.189 bits, and, accordingly, dissipates at least ~ 0.02 eV of heat. With the unpopular OR-NOT today, the situation is similar.
Things are not better with memory cells, any entry in which leads to the destruction of previous values. For a programmer, old data is simply “lost”, but laws of conservation of charge and energy do not allow them to get lost “just like that” on a physical level. In fact, old information is not destroyed, it is scattered in space in the form of heat and spurious radiation.
For more than 30 years, a method of organizing calculations without destroying information has been known, which does not fall under the Landauer principle and allows the creation of theoretically energy-efficient processors. This method is called conservative, or "preserving", logic. Unfortunately, it was not possible for him to create a compact physical implementation in silicon, only the method of implementation on MOS transistors with poorly miniaturized inductors is known. On the other hand, this approach is natural for most types of quantum computers, including optical ones (Benioff’s model, etc.)
Over the years, it turned out that conservative logic turned out to be a useful mathematical abstraction without implementation "in hardware": block cellular automata are created on its basis, which are very convenient to use when solving problems "for limited resources." This branch of mathematics is now very actively developing, and, perhaps, in a decade or so, block cellular automata will be even more famous among programmers than ordinary ones.
The “butterfly wing flap” that led to the appearance of this article was the question raised by Comrade Plakhov, “How is it in Russian?”, The answer to which even Yandex does not know. In addition to the 2004 article in Computerra mentioned above, there is no information on conservative logic in Russian at all - all the more offensive, since its theoretical foundations were laid down by the great Soviet physicists Landau and Lifshits exactly 50 years ago, in 1961. In order to at least slightly eliminate this gap, on the one hand, and not “smack the gag,” on the other, I bring to your attention an abstract (translation of the main points) of a fundamental article on the conservative logic of Eduard Fredkin and Tomasso Toffoli published in the journal Theoretical Physics No. 21 for 1982. (Fredkin, Edward and Toffoli, Tomasso, “Conservative Logic”, Int. J. Theor. Phys. 21 (1982), 219–253;pdf ). This article reveals all the main points regarding the physics, logic, and circuitry of systems based on conservative logic.
Conservative logic
Conservative or conservation logic is a mathematical model of the organization of calculations based on two fundamental physical principles: reversibility of processes and conservation laws.
1. Physical fundamentals
(The numbering of sections of the abstract does not coincide with the numbering of parts of the article - approx. Per. )
Any calculation, no matter how it is performed, by a person or by a machine, must obey certain physical laws. In particular, the speed of information dissemination is limited by the speed of light, and the amount of information in the final system must also be finite. There are more complex limitations.
All physical laws can be divided into dynamic and statistical. The former describe the behavior of individual objects in fully defined microscopic systems and allow, in classical mechanics, to accurately predict the outcome of any experiment. When there are too many objects to calculate each of them, statistical laws are applied that describe the average behavior of homogeneous objects in the macro system. They allow you to evaluate the picture as a whole, but do not provide an opportunity to predict the behavior of a particular object.
At the micro level, our world has various fundamental homogeneities and symmetries, many of which lead to the emergence of "conservation laws" at the macro level. Thus, the uniformity of time ensures the fulfillment of the law of conservation of energy, the uniformity of space - the law of conservation of momentum, and the isotropy of space (symmetry of directions) leads to the conservation of the moment of rotation.
All dynamic fundamental physical laws are reversible in the sense of replacing coordinates by inverse ones. You can reverse the beat in billiards if you let all the balls go in the strictly opposite direction. On the other hand, statistical physical laws obey the principles of thermodynamics and are not reversible without reversing the arrow of time; a broken vase will never be assembled from fragments. In particular, the traditional computational model operating at the macro level is based on the AND-NOT or OR-NOT gates. Any calculation in such a model requires energy costs in accordance with the Landauer principle.
In any organization of computations, digital information physically represents the numbered stable states of any systems.
Note trans. : the article is intended for physicists, therefore, the authors do not give illustrations to things obvious to physicists. The last sentence is about this: for example, the capacitor of a memory cell can be in two logical states - “charged” or “discharged” (although, of course, the “physical” charge of the capacitor is practically continuous, but not Boolean). The stability of these logical states is ensured by a special electronic regeneration circuit that recharges the charged capacitors and discharges the discharged ones. In this case, the difference in energy between the “charged” and “discharged” states should be huge compared to the level of thermal noise, otherwise damage to stored values is possible.
Although in fact these states can be electrical, optical, etc., hereinafter we will call them “mechanical” to distinguish them from thermodynamic states. Thermodynamic states are degrees of freedom of individual atoms and molecules that make up a substance. In one gram of any substance there is a huge, about 10 23 (Avogadro number), the number of such degrees of freedom, and they can be taken into account only by statistical methods and laws.
The second law of thermodynamics says that the total entropy of a closed system cannot decrease. The Landauer principle establishes the energy relationship between informational and thermodynamic entropy. Many algorithms lead to a decrease in information entropy, but such a decrease should either be compensated by an increase in thermodynamic entropy (heat generation), or it should be prohibited.
Accordingly, two fundamentally different approaches to the physical organization of calculations are possible.
With a “conservative” or “preserving” approach for storing information, mechanical conditions are selected for which the entropy exchange with thermodynamic states is impossible. In such a system, any operations that reduce information entropy, in particular, information destruction operations, should be prohibited. Therefore, all operations must be reversible. Landau and Livshits showed that in such a system there must exist some invariant additive quantities, for example, charges or moments “protected” by the conservation law - only then will the transition of “charges” to “temperature” and vice versa be impossible. The total level of these quantities available in a closed system will be constant and independent of the processes occurring in the system.
Unlike the conservative one, with the usual “von Neumannian” approach, calculations are initially irreversible. To satisfy the second law of thermodynamics, there must exist a path for the exchange of entropy and energy between the mechanical and thermodynamic degrees of freedom. Such a path should be one-sided (i.e. irreversible) so that thermal fluctuations cannot destroy the information stored in mechanical states. But, since at the micro level all processes are reversible, it is possible to achieve a one-sided flow of entropy only if the energy difference between the mechanical states is much orders of magnitude greater than between the thermodynamic ones. In modern computer technology (1982 - approx. Trans. ) The difference is from 8 to 12 orders of magnitude.
Note trans. : Imagine that our system consists of a very small W-shaped glass and a ball in it. The ball has two stable positions - at the bottom of the left and right halves of the glass. These are mechanical states that can be numbered and store information in them. To "write" new information into the glass, in the sense of changing the position of the ball, you need to raise the ball up the hill in the center of the glass, spending a certain amount of energy on this rise. Then, already on the other side of the glass, this surplus of energy needs to be taken back or somehow extinguished, otherwise the ball will oscillate with a large amplitude around the equilibrium position. No matter how the process of selection of excess energy is organized, part of it will turn into heat anyway, but the smaller the "height of the hill", the less energy loss will be.
Now imagine that in a real system both the ball and the glass experience constant thermal fluctuations. The strength of such vibrations is proportional to temperature. While the temperature is low, the ball, although not always perfectly located at the equilibrium point, but at least often returns to it. But with increasing temperature, the fluctuations intensify, and at some point the ball gets a chance to spontaneously "jump" over the hill. In no case should this be allowed, therefore the “slide” should be very high - with inevitably high energy costs for its regular overcoming.
All of today's computing technology is built on a second, "irreversible" path. Irreversibility is specially laid down in the basic logic circuits, in pn junctions of transistors, and even if the calculated high-level algorithm is formally reversible - when executed on modern processors, at least part of its individual steps is irreversible at the lowest level. Irreversibility also means high heat dissipation, which limits achievable performance.
2. The basic elements of conservative logic
Computational models based on the conservative principle should use basic logic elements that satisfy certain conditions. In particular, they must be reversible and preserve the very additive quantities (charges, moments). From the second requirement it follows that the number of inputs of an element must be equal to the number of outputs, which, in turn, means a functional composition strictly “one to one”.
Note trans. : in conventional circuitry, the output of one logic element can be connected to the inputs of several other elements (“branching”). In conservative circuitry, one output must go strictly to one input of the next element; branching requires a special logic element (see below).
Conservative logic is based on two elements - the repeater and the Fredkin gate.
The repeater (unit wire; literally "elementary conductor") simply repeats the output signal fed to its input, with a delay of 1 clock cycle. It is the speed of the repeaters that determines the clock frequency of the circuit. Formally, the repeater function is expressed as:
y t = x t-1
Legend: The
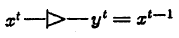
repeater can perform the functions of both storing (being closed to itself) and transmitting information inside the circuit, but its main task is to synchronize signals with a clock generator.
The element opposite to the repeater is the same repeater, but directed in the opposite direction.
The values at the outputs of the repeaters on a particular clock cycle completely describe the internal state of the digital circuit of the conservative logic, that is, the outputs of the repeaters are state variables of such a circuit. The sum of the values at the outputs of the repeaters will be that same additive stored value (“total charge”), and, for a closed system, a constant value. The total number of repeaters in the circuit can be regarded as the number of degrees of freedom of this circuit.
Repeaters are remotely similar, but far from equivalent, to delay elements in conventional “von Neumann” circuitry.
Fredkin's Gate- this is a device with three inputs u, x1, x2 and three outputs v, y1, y2, which implements the function of controlled “overlap” (“cross”) of two data lines (see. Fig.). Output v always matches input u. For u = 1, the outputs y1, y2 are equal to the inputs x1, x2; for u = 0, y1 = x2 and y2 = x1 (see table).

The truth table of the Fredkin gate:
(u, x1, x2) => (v, y1, y2)
0,0,0 => 0,0,0
0,0,1 => 0,1,0
0,1,0 => 0,0,1
0,1,1 => 0,1,1
1,0,0 => 1,0,0
1, 0.1 => 1,0,1
1,1,0 => 1,1,0
1,1,1 => 1,1,1
Fredkin gate is opposite to itself.
Thus, any circuit in conservative logic is a controllable conditional signal router, at the outputs of which a certain controllable rearrangement of input values at previous clock cycles is formed.
3. Conservative circuitry
In conservative logic, it is possible to implement a Turing machine (Bennett, 1973) and a universal cellular automaton (Toffoli, 1980). Thus, conservative logic allows one to solve any Church computable problems.
The process of implementing arbitrary functions in conservative logic is very similar to the same process in traditional logic.
As in traditional circuitry, when implementing some functions, constants are used - sources of constant values 0 or 1. On the other hand, as a result of calculations, not only the required results can be obtained, but also side ones that are not needed for further use in a particular algorithm. The side effects obtained are called “garbage” or “sinks”. Since in conservative logic the signals do not appear “out of nowhere” and do not disappear “to nowhere”, it is simply impossible to discard lines with “unnecessary” results, they must be disposed of in a special way (scattered in space).
The figure shows the legend for the unit of calculation of a certain function φ:

This is how the block " I " is arranged :

(note that one of the sinks is a copy of the argument)
The following figure shows the implementation of the logical functions " OR " (a), " NOT " (b) and the signal splitter 2a-a. The last two differ only in the logical role of the conclusions.

The following diagram shows a simple memory element, a JK trigger . A question mark indicates a drain that does not have any meaningful meaning.

The following is a more complex scheme: a demultiplexer sending a signal X to the binary address A0, A1 to one of the four outputs Y0 - Y3:

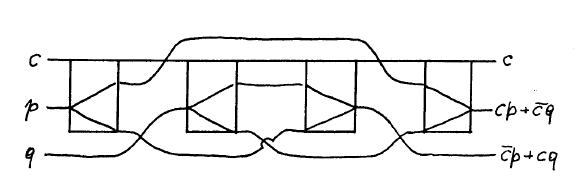
In conservative logic, any circuit from “ordinary” logic can be implemented. For example, the following three figures show the implementation of a single-bit sequential adder : the first in conventional logic (in the old notation), and the second and third in a conservative one. Moreover, the second scheme is assembled by simply substituting substitutions for the first, and the third is created “from scratch”. The difference between the repeaters and the delay elements is visible on the circuits: in conservative circuits, the signals are synchronized explicitly.



4. The problem of drains
The practical value of conservative logic, if implemented, for example, in quantum computers, depends entirely on the number of drains requiring utilization in real calculations. Destruction of drains is the same “energy-generating” operation, which is also inherent in conventional circuitry. If for each trigger of the processor there will be its own drain, there will be no gain in energy release.
It is impossible to completely avoid the appearance of drains. For example, in many real-world algorithms, the final result is the sum of any numbers. But the summation operation itself is irreversible, since, knowing only its result, it is impossible to determine the initial terms. In a universal processor that executes in turn many different programs and algorithms, there will be too much such “extra” information to be simply collected. A special “entropy exchanger” will be required, into which the waste results will be delivered.
Depending on the type of function being calculated, there are three possible scenarios for the ratio of the number of necessary constants and sinks (see Fig.):

The third, best scenario is possible only if the calculated function f itself is reversible and obeys the current conservation laws.
There is a way to partially solve the drain problem, and at the same time to order the generation of constants using inverted circuits. By “inverted” is meant a circuit reversing a given one, that is, restoring inputs and constants from given outputs and drains. Since all circuits in conservative logic are reversible, for the inversion of the circuit it is enough to simply turn all the repeaters in the opposite direction and call the inputs the outputs; or, which is the same thing, reflect the scheme in the mirror (see. Fig.).
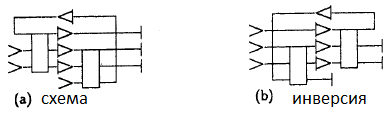
The direct and inverted circuit can be connected in series with each other. The element obtained in this way will duplicate its inputs with a long delay, without requiring any constants and without creating drains, but somewhere inside it will have the results of the calculations of the original function (see. Fig.).

The calculated values of the original function can be "pulled out" if you "embed" spy splitters into the circuit:

To use such a circuit, you still need to provide constants (more precisely, a scratchpad register that needs to be filled in once with the required zeros and ones) , and also correctly fill in both the output and output registers. The output of such a scheme is a) a copy of the arguments, b) the result, and c) the inversion of the result, and if any of this is not used anywhere else, then they will also have to be disposed of.
The main advantage of this method is that the number of "drain" lines is proportional to only the bit depth of the input. At the same time, the number of gates needed to implement most of the real functions in any logic grows approximately as an exponent of the input bit depth. In conventional circuitry, all valves release heat, in conservative - only "drain", therefore, with a large bit depth of the inputs, the benefit should be huge.
5. The model of billiard balls
This part presents an abstract physical model in which conservative logic is implemented.
The model is a plane along which billiard balls move without friction in strictly specified directions. The velocities, permissible directions, and sizes of the balls are selected in such a way that at discrete time instants corresponding to measures, the balls can only be in a small set of points forming a rectangular grid rotated by 45 '(see Fig.). If the balls fall into neighboring points, an elastic collision occurs between them.

The logical unit is the presence of the ball, and zero - its absence.
An arbitrary grid point can be declared a “interaction gate” if the trajectories of two balls intersect in it. The direction of exit of these balls depends on the presence of both:

On the plane, fixed walls or mirrors can be installed. Using mirrors, you can rotate (a), shift (b), hold, and safely cross the paths (d) of the balls. The last element (d) is called a “nontrivial crossover” and allows the balls to “pass through each other”.

It is possible to create managed switches. The figure shows: a block diagram of a simple switch, the designation of the inverse switch element, as well as a diagram of the implementation of a simple switch.
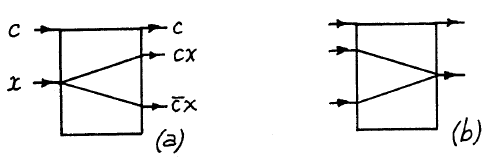

Finally, from simple switches and a non-trivial crossover (indicated by a “bridge”), you can construct a Fredkin valve (turning mirrors and delays are not shown for clarity):

As for the real physical embodiment, the molecules of gas are more suitable for the role of balls, rather than real billiard balls, although neither one nor the other option has ever been implemented.
The main advantage of the billiard balls model is its simplicity: thanks to specially selected angles and speeds, the results of all collisions can be calculated by simple Boolean functions, without the participation of floating-point numbers, costly rounding operations, etc. This allows you to quickly simulate even very large schemes of conservative logic on traditional computers.
6. “Complex” questions about conservative logic
1. Are arbitrary calculations possible in conservative logic? Yes, possible, conservative logic is Turing-complete.
2. Are there physical effects on which conservative logic can be implemented? Yes, it can be implemented on the basis of electronic elements (discrete L / R / C elements plus MOS transistors) (in practice, by 2011 everything remains only on paper and in laboratories - approx. Per. )
3. Will there be energy needed for waste disposal, more than the potential gain from switching to conservative logic? A complete answer to this question cannot be given without taking into account a specific physical model, but the method of hiding drains described in Section 4. leaves very high chances for a negative (in the sense of an optimistic) answer.
4. Finally, the question of the stability of the system to low noise is still unanswered.
Instead of a conclusion (from a translator)
The very fact that by controlledly mixing the wiring in a bundle or cable between the input and output and not using any other elements except “overlap” and repeaters, you can get the result of calculating any function from the input at the output is far from obvious. The underlying computational logic is unusual, but unlike other Turing-complete mathematical abstractions, such as Markov algorithms, it looks very “technological”, ready for use in real processors. Quite possibly, quantum computers will work on something similar, adjusted for purely quantum "tricks." If we combine conservative quantum logic with superconducting interconnects, we can build a computer that is practically practically not absorbing energy. Well, the future will show.
