Visualization Methods in Multidimensional Games
... A couple of years ago there was already a topic on a similar topic, I want to share my thoughts ...
One of the problems that arise when writing a game whose action space contains more than three spatial dimensions is the visualization of the action scene, sufficiently understandable to the user, and suitable for management as a character (or object) of the game, and a virtual camera that creates the image.
Most of the multidimensional games that I have come across lately have been puzzles - analogues of the Rubik's Cube. But for different dimensions of the puzzle, the authors had to use various visualization methods.
In these games, the working object is a convex four-dimensional polyhedron, most often having a high degree of symmetry (for example, equilateral). Initially, each of its faces is painted in its own color, but when the faces are rotated, the colors are mixed. The goal is to restore the original color order.
All vertices of the polyhedron lie on a four-dimensional sphere. For visualization, a stereographic projection of this grid (a set of vertices) onto a three-dimensional space is taken, and three-dimensional polyhedra are constructed in it — projections of the faces of the original cube. Faces are divided into smaller polyhedra (“stickers” - analogues of small squares in a regular cube), which have a slightly smaller size (so that you can see the internal stickers, if any). The resulting model is depicted in a 3D viewer with a camera constantly pointing at the center of the model. In the particular case of a tesseract, 7 faces are visible, this is enough for the game. You can control the focal length of the camera (viewing angle) and the distance from the camera to the center.

Visualization goes about the same, but the stereographic projection goes to 4-dimensional space. Further, it is prospectively projected onto three-dimensional. Four-dimensional stickers are depicted as rib models, the colors of the edges correspond to the colors of the original stickers.

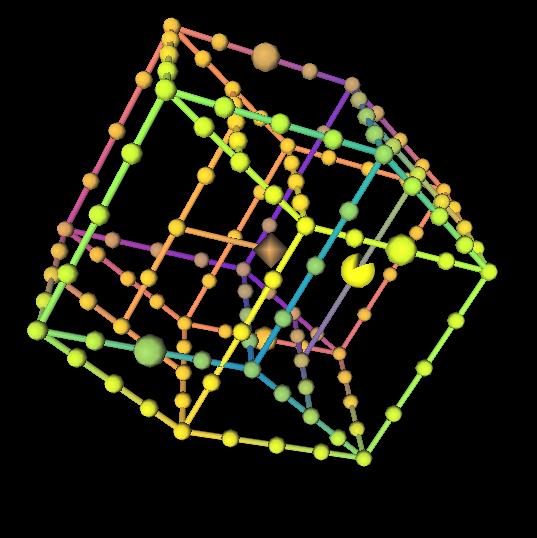
Four “primary” measurements and three “additional” are selected. We consider 7 faces in the main dimensions, each of them is a six-dimensional cube. This cube is represented in a fractal way: it is divided according to the main measurements into N ^ 3 cubes, each of which, in turn, consists of N ^ 3 stickers in additional dimensions.
The main faces are located in the same way as the faces of a 4-dimensional cube in a stereographic projection.
To show at least part of the faces in additional dimensions, their stickers are considered. adjacent to the “main” faces, and are placed on the surface of small cubes of each face (thereby, they turn out to be not N ^ 3, but (N + 2) ^ 3).
As it turns out, it’s quite possible to assemble such a seven-dimensional cube.

It does not even use a three-dimensional viewer - the projection goes immediately to 2D. We look at the glass from above, we see a rectangular parallelepiped, each cell of which is filled up to its own height. Cells are depicted in a standard way (a rectangle consisting of diagonal chains of cells), the height is color-coded. The falling figure is represented firstly by its wireframe model, secondly, by the shadow (part of the cells are shaded), and thirdly, on the vertical projection of the glass (where the order of colors and the position of the figure are visible)
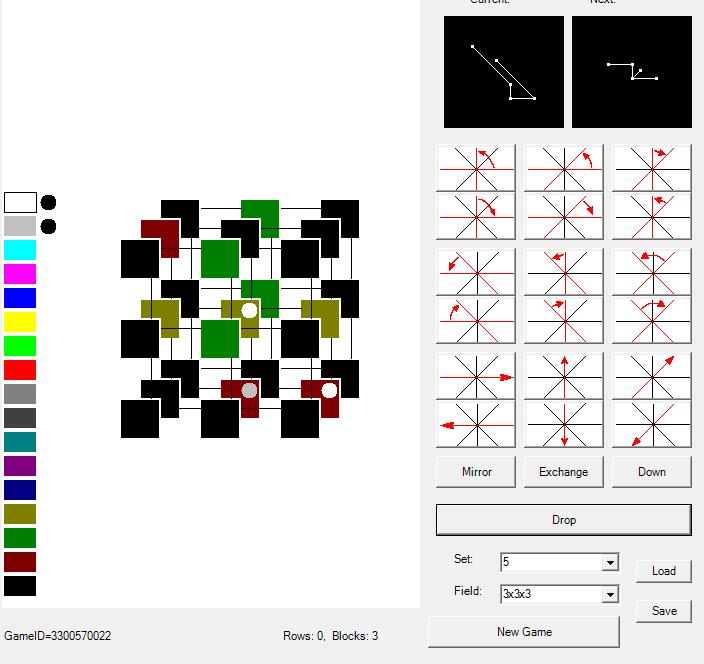
A wireframe maze model is used (segments that you can walk along). The model is projected into three-dimensional space (additional coordinates are shown in color - yellow-violet axis for U and red-blue axis for V). The maze is shown in the 3D viewer. You can rotate the camera (it also serves to control the packman) both in 3D (right / left and up / down) and in the color space (in the yellow, violet, blue, etc. sides). These turns look like skews of the model - some of the vertices are approaching, some are being removed, and some parts of the maze change color.
For visualization, a regular 3D viewer is used, the camera is inside the space, the rays propagate along straight lines (geodesic of the Lobachevsky space). The camera sensor is almost flat.

There is another way of visualization (used in the BlockBuilding game ) - honest vision with a three-dimensional retina: first it is calculated what the camera sees (this is a colored three-dimensional space), and then it is projected onto 2D. This probably makes sense only when rendering as line segments or translucent 2D faces.
One of the problems that arise when writing a game whose action space contains more than three spatial dimensions is the visualization of the action scene, sufficiently understandable to the user, and suitable for management as a character (or object) of the game, and a virtual camera that creates the image.
Most of the multidimensional games that I have come across lately have been puzzles - analogues of the Rubik's Cube. But for different dimensions of the puzzle, the authors had to use various visualization methods.
Four-dimensional analogues of the Rubik's Cube
In these games, the working object is a convex four-dimensional polyhedron, most often having a high degree of symmetry (for example, equilateral). Initially, each of its faces is painted in its own color, but when the faces are rotated, the colors are mixed. The goal is to restore the original color order.
All vertices of the polyhedron lie on a four-dimensional sphere. For visualization, a stereographic projection of this grid (a set of vertices) onto a three-dimensional space is taken, and three-dimensional polyhedra are constructed in it — projections of the faces of the original cube. Faces are divided into smaller polyhedra (“stickers” - analogues of small squares in a regular cube), which have a slightly smaller size (so that you can see the internal stickers, if any). The resulting model is depicted in a 3D viewer with a camera constantly pointing at the center of the model. In the particular case of a tesseract, 7 faces are visible, this is enough for the game. You can control the focal length of the camera (viewing angle) and the distance from the camera to the center.

Five-dimensional Rubik's Cube
Visualization goes about the same, but the stereographic projection goes to 4-dimensional space. Further, it is prospectively projected onto three-dimensional. Four-dimensional stickers are depicted as rib models, the colors of the edges correspond to the colors of the original stickers.

Seven-dimensional cube
Four “primary” measurements and three “additional” are selected. We consider 7 faces in the main dimensions, each of them is a six-dimensional cube. This cube is represented in a fractal way: it is divided according to the main measurements into N ^ 3 cubes, each of which, in turn, consists of N ^ 3 stickers in additional dimensions.
The main faces are located in the same way as the faces of a 4-dimensional cube in a stereographic projection.
To show at least part of the faces in additional dimensions, their stickers are considered. adjacent to the “main” faces, and are placed on the surface of small cubes of each face (thereby, they turn out to be not N ^ 3, but (N + 2) ^ 3).
As it turns out, it’s quite possible to assemble such a seven-dimensional cube.

Four-dimensional tetris
It does not even use a three-dimensional viewer - the projection goes immediately to 2D. We look at the glass from above, we see a rectangular parallelepiped, each cell of which is filled up to its own height. Cells are depicted in a standard way (a rectangle consisting of diagonal chains of cells), the height is color-coded. The falling figure is represented firstly by its wireframe model, secondly, by the shadow (part of the cells are shaded), and thirdly, on the vertical projection of the glass (where the order of colors and the position of the figure are visible)

> Five-dimensional packman
A wireframe maze model is used (segments that you can walk along). The model is projected into three-dimensional space (additional coordinates are shown in color - yellow-violet axis for U and red-blue axis for V). The maze is shown in the 3D viewer. You can rotate the camera (it also serves to control the packman) both in 3D (right / left and up / down) and in the color space (in the yellow, violet, blue, etc. sides). These turns look like skews of the model - some of the vertices are approaching, some are being removed, and some parts of the maze change color.

Puzzle in the Lobachevsky space
For visualization, a regular 3D viewer is used, the camera is inside the space, the rays propagate along straight lines (geodesic of the Lobachevsky space). The camera sensor is almost flat.

"Three-dimensional retina"
There is another way of visualization (used in the BlockBuilding game ) - honest vision with a three-dimensional retina: first it is calculated what the camera sees (this is a colored three-dimensional space), and then it is projected onto 2D. This probably makes sense only when rendering as line segments or translucent 2D faces.
