JPEG decoding for dummies
- Tutorial
UPD I was forced to remove the monospace formatting. One fine day, the habraparser stopped perceiving formatting inside the pre and code tags. The whole text turned into a mess. Habr administration could not help me. Now it’s rugged, but at least readable.
[FF D8]
Have you ever wanted to know how a jpg file works? Now let's figure it out! Warm up your favorite compiler and hex editor, we will decode it:

Specially took a smaller picture. This is Google’s familiar but tightly squeezed favicon: I
warn you right away that the description is simplified and the information given is not complete, but then it will be easy to understand the specification.
Even without knowing how encoding occurs, we can already extract something from the file.
[FF D8]- start marker. It is always at the beginning of all jpg files.
Following are the bytes [FF FE] . This is a marker indicating the beginning of a comment section. The next 2 bytes [00 04] are the length of the section (including these 2 bytes). So in the next two [3A 29] - the comment itself. These are the character codes ":" and ")", i.e. regular emoticon. You can see it in the first line of the right side of the hex editor.
Very briefly on the steps:

I remind you that each block Y ij , Cb ij , Cr ij is a matrix of DCT coefficients encoded by Huffman codes. In the file they are arranged in the following order:Y 00 Y 10 Y 01 Y11 Cb 00 Cr 00 Y 20
After we have extracted the comment, it will be easy to understand that:
FF D8 FF FE 00 04 3A 29 FF DB 00 43 00 A0 6E 78
8C 78 64 A0 8C 82 8C B4 AA A0 BE F0 FF FF F0 DC
DC F0 FF FF FF FF FF FF FF FF FF FF FF FF FF FF
FF FF FF FF FF FF FF FF FF FF FF FF FF FF FF FF
FF FF FF FF FF FF FF FF FF FF FF FF FF DB 00
43 01 AA B4 B4 F0 D2 F0 FF FF FF FF FF FF FF FF
FF FF FF FF FF FF FF FF FF FF FF FF FF FF FF FF
FF FF FF FF FF FF FF FF FF FF
FF FF FF FF FF FF FF FF FF FF FF FF FF FF FF FF
FF FF FF C0 00 11 08 00 10 00 10 03 01 22 00 02
11 01 03 11 01 FF C4 00 15 00 01 01 00 00 00 00
00 00 00 00 00 00 00 00 00 00 00 03 02 FF C4 00 1A
10 01 00 02 03 01 00 00 00 00 00 00 00 00 00 00 00
00 01 00 12 02 11 31 21 FF C4 00 15 01 01 01 00 00
00 00 00 00 00 00 00 00 00 00 00 00 00 00 01 FF
C4 00 16 11 01 01 01 00 00 00 00 00 00 00 00 00
00 00 00 00 00 11 00 01 FF DA 00 0C 03 01 00 02 11
03 11 00 3F 00 AE E7 61 F2 1B D5 22 85 5D 04 3C
82 C8 48 B1 DC BF FF D9
FF DB 00 43 00 A0 6E 78
8C 78 64 A0 8C 82 8C B4 AA A0 BE F0 FF FF F0 DC
DC F0 FF FF FF FF FF FF FF FF FF FF FF FF FF
FF FF FF FF FF FF FF FF FF FF FF FF FF FF FF FF
FF FF FF FF FF FF FF FF FF FF FF FF FF
The section header always takes 3 bytes. In our case, it is [00 43 00]. The header consists of:
[00 43] Length: 0x43 = 67 bytes
[0_] Length of the values in the table: 0 (0 - 1 byte, 1 - 2 bytes)
[_0] Table ID: 0
The remaining 64 bytes need to be filled in the 8x8 table .
[A0 6E 64 A0 F0 FF FF FF]
[78 78 8C BE FF FF FF FF]
[8C 82 A0 F0 FF FF FF FF]
[8C AA DC FF FF FF FF FF]
[B4 DC FF FF FF FF FF FF]
[F0 FF FF FF FF FF FF FF]
[FF FF FF FF FF FF FF FF]
[FF FF FF FF FF FF FF FF]
Take a look at the order in which the values in the table are filled. This order is called the zigzag order:
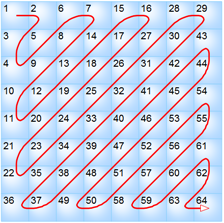
This marker is called SOF0, and means that the image is encoded using the basic method. It is very common. But on the Internet, the progressive method you are familiar with is no less popular when you first download a low-resolution image, and then a normal picture. This allows you to understand what is shown there, without waiting for a full download. The specification defines a few more, it seems to me, not very common methods.
FF C0 00 11 08 00 10 00 10 03 01 22 00 02
11 01 03 11 01
[00 11] Length: 17 bytes.
[08] Precision: 8 bits. The base method is always 8. As I understand it, this is the bit depth of the channel values.
[00 10] Pattern height: 0x10 = 16
[00 10] Pattern width: 0x10 = 16
[03] Number of components: 3. Most often it is Y, Cb, Cr.
1st component:
[01] Identifier: 1
[2_] Horizontal decimation (H 1 ): 2
[_2] Vertical decimation (V 1 ): 2
[00] Quantization table identifier: 0
2nd component:
[02] Identifier : 2
[1_] Horizontal decimation (H 2 ): 1
[_1] Vertical decimation (V 2 ): 1
[01] Quantization table identifier: 1
3rd component:
[03] Identifier: 3
[1_] Horizontal decimation (H3 ): 1
[_1] Vertical decimation (V 3 ): 1
[01] Quantization table identifier: 1
Now look at how to determine how thin the image is. We findH max = 2 and V max = 2 . Channel i will be thinned out H max / H i times horizontally and V max / V i times vertically.
This section stores codes and values obtained by Huffman coding .
FF C4 00 15 00 01 01 00 00 00 00
00 00 00 00 00 00 00 00 00 00 03 02
[00 15] Length: 21 bytes.
[0_] class: 0 (0 - table of DC coefficients, 1 - table of AC coefficients).
[_0] table identifier: 0
Huffman code length: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
Number of codes: [01 01 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00]
Number of codes means the number of codes of this length. Please note that the section stores only the code lengths, not the codes themselves. We must find the codes ourselves. So, we have one code of length 1 and one of length 2. Total 2 codes, there are no more codes in this table.
Each code has a value associated with it; they are listed next in the file. The values are single-byte, so we read 2 bytes.
[03] - the value of the 1st code.
[02] - the value of the 2nd code.
Further in the file you can see 3 more markers [FF C4], I will skip the analysis of the corresponding sections, it is similar to the above.
We need to build a binary tree from the table we got in the DHT section. And already on this tree we recognize each code. We add the values in the order shown in the table. The algorithm is simple: no matter what node we are in, we always try to add a value to the left branch. And if she is busy, then to the right. And if there is no place there, then we return to a level higher and try from there. You need to stop at a level equal to the length of the code. Left branches correspond to thevalue 0 , right branches - 1 .
Note:
You do not have to start from the top every time. Added value - return to the level above. Does the right branch exist? If so, go up again. If not, create the right branch and go there. Then, from this point, start your search to add the next value.
The trees for all the tables in this example are:
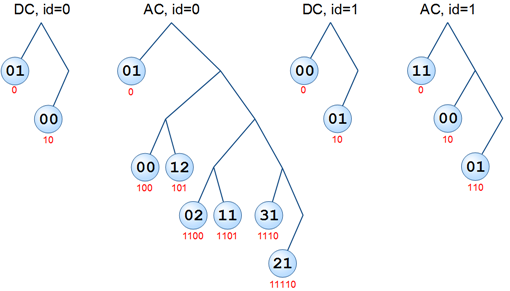
UPD (thanks anarsoul ): The nodes of the first tree (DC, id = 0) should have the values 0x03 and 0x02.
In the circles are the code values, under the circles are the codes themselves (I will explain that we got them by going through path from the top to each node). It is with these codes (this and other tables) that the very content of the picture is encoded.
Byte [DA] in the marker means - “YES! Finally, we went directly to parsing the encoded image section! ” However, the section is symbolically called SOS.
FF DA 00 0C 03 01 00 02 11
03 11 00 3F 00
[00 0C] The length of the header part (and not the entire section): 12 bytes.
[03] Number of scan components. We have 3, one per Y, Cb, Cr.
1st component:
[01] Image component number: 1 (Y)
[0_] Huffman table identifier for AC coefficients: 0
[_0] Huffman table identifier for AC coefficients: 0
2nd component:
[02] Image component number: 2 (Cb)
[1_]Huffman table identifier for DC coefficients: 1
[_1] Huffman table identifier for AC coefficients: 1
3rd component:
[03] Image component number: 3 (Cr)
[1_] Huffman table identifier for DC coefficients: 1
[_1] Identifier Huffman tables for AC coefficients: 1
These components cyclically alternate.
[00], [3F], [00] These bytes can be read in the specification.
This ends the header part, from here to the end (marker [FF D9]) encoded data.
[AE] [E7] [61] [F2] [1B]
101011101110011101100001111100100
Finding a DC coefficient.
1.We read the sequence of bits (if we meet 2 bytes [FF 00], then this is not a marker, but just a byte [FF]) . After each bit, we move along the Huffman tree (with the corresponding identifier) along the 0 or 1 branch, depending on the read bit. We stop if we are in the final node.
101011101110011101100001111100100
2. Take the value of the node. If it is 0, then the coefficient is 0, write to the table and go on to reading other coefficients. In our case - 02. This value is the length of the coefficient in bits. That is, we read the next 2 bits, this will be the coefficient.
101011101110011101100001111100100
3. If the first digit of the value in binary representation is 1, then leave it as it is: DC_coef = value. Otherwise, we transform:DC_coef = value-2 value length +1 . We write the coefficient into the table at the beginning of the zigzag - the upper left corner.
Finding AC coefficients.
1. Similar to paragraph 1, finding the DC coefficient. We continue to read the sequence:
101011101110011101100001111100100
2. We take the value of the node. If it is 0, this means that the remaining matrix values must be filled with zeros. The next matrix is encoded further. The first few who read up to this place and wrote about it to me in PM will receive a plus in karma. In our case, the value of the node: 0x31.
First nibble: 0x3 - this is how many zeros we need to add to the matrix. These are 3 zero coefficients.
Second nibble: 0x1 - coefficient length in bits. Read the next bit.
101011101110011101100001111100100
3. Similar to item 3 of finding the DC coefficient.
As you already understood, you need to read AC-coefficients until we come across a zero value of the code, or until the matrix is filled.
In our case, we get:
101011101110011101100001111100100
and the matrix:
[2 0 3 0 0 0 0 0]
[0 1 2 0 0 0 0 0]
[0 -1 -1 0 0 0 0 0]
[1 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0]
You noticed that the values are filled in same zigzag pattern?
The reason for using this order is simple - since the larger the values of v and u, the less significant is the coefficient S vu in the discrete cosine transform. Therefore, at high compression ratios, unimportant coefficients are reset to zero, thereby reducing the file size.
Similarly, we get 3 more Y-channel matrices ...
[-4 1 1 1 0 0 0 0] [5 -1 1 0 0 0 0 0]
[0 0 1 0 0 0 0 0] [-1 -2 -1 0 0 0 0 0]
[0 -1 0 0 0 0 0 0] [0 -1 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0] [-1 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0] [0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0] [0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0] [0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0] [0 0 0 0 0 0 0 0]
[-4 2 2 1 0 0 0 0]
[-1 0 -1 0 0 0 0 0]
[-1 -1 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0 0]
Oh, I forgot to say that the encoded DC coefficients are not the DC coefficients themselves, but their differences between the coefficients of the previous table (the same channel)! You need to correct the matrix:
DC for the 2nd: 2 + (-4) = -2
DC for the 3rd: -2 + 5 = 3
DC for the 4th: 3 + (-4) = -1
[-2 1 1 1 0 0 0 0] [3 -1 1 0 0 0 0 0] [-1 2 2 1 0 0 0 0]
...........
Now the order. This rule is valid until the end of the file.
... and according to the matrix for Cb and Cr:
[-1 0 0 0 0 0 0 0] [0 0 0 0 0 0 0 0]
[1 1 0 0 0 0 0 0] [1 -1 0 0 0 0 0 0 ]
[0 0 0 0 0 0 0 0] [1 0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0] [0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0] [0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0] [0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0] [0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0] [0 0 0 0 0 0 0 0]
Since there is only one matrix, DC coefficients can not be touched.
Do you remember that the matrix goes through the quantization stage? The elements of the matrix must be multiplied termwise with the elements of the quantization matrix. It remains to choose the right one. First, we scanned the first component, its image component = 1. The image component with this identifier uses the quantization matrix 0 (we have the first of two). So, after the multiplication:
[320 0 300 0 0 0 0 0]
[0 120 280 0 0 0 0 0]
[0 -130 -160 0 0 0 0 0]
[140 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0]
Similarly, we get 3 more Y-channel matrices ...
[-320 110 100 160 0 0 0 0] [480 -110 100 0 0 0 0 0]
[0 0 140 0 0 0 0 0] [-120 -240 -140 0 0 0 0 0]
[0 -130 0 0 0 0 0 0] [0 -130 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0 0] [-140 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0] [0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0] [0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0] [0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0] [0 0 0 0 0 0 0 0 0]
[-160 220 200 160 0 0 0 0]
[-120 0 -140 0 0 0 0 0]
[-140 - 130 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0]
... and in the matrix for Cb and Cr.
[-170 0 0 0 0 0 0 0] [0 0 0 0 0 0 0 0 0]
[180 210 0 0 0 0 0 0] [180 -210 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0] [240 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0] [0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0] [0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0] [0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0] [0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0 0] [0 0 0 0 0 0 0 0 0]
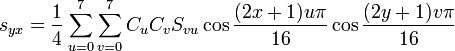

The formula should not be difficult *. S vu is our obtained matrix of coefficients. u is a column, v is a row. s yx are the channel values themselves.
* Generally speaking, this is not entirely true. When I was able to decode and display a 16x16 picture, I took a 600x600 image (by the way, it was the cover of my favorite Mind.In.A.Box album - Lost Alone). It didn’t work right away - various bugs surfaced. Soon I could admire the correctly uploaded picture. Only very upset the download speed. I still remember, it took 7 seconds. But this is not surprising, if you use the above formula thoughtlessly, then to calculate one channel of one pixel, you will need to find 128 cosines, 768 multiplications, and some additions there. Just think about it - almost a thousand difficult operations on only one channel of one pixel! Fortunately, there is scope for otimization (after long experiments, I reduced the load time to a timer accuracy limit of 15ms, and after that changed the image to a photograph 25 times larger. Perhaps I will write about this in a separate article).
I will write the result of calculating only the first matrix of channel Y (the values are rounded):
[138 92 27 -17 -17 28 93 139]
[136 82 5 -51 -55 -8 61 111]
[143 80 -9 -77 -89 -41 32 86]
[157 95 6 -62 -76 -33 36 86]
[147 103 37 -12 -21 11 62 100]
[87 72 50 36 37 55 79 95]
[-10 5 31 56 71 73 68 62]
[- 87 -50 6 56 79 72 48 29]
and the two remaining:
Cb Cr
[60 52 38 20 0 -18 -32 -40] [19 27 41 60 80 99 113 120]
[48 41 29 13 -3 -19 -31 -37] [0 6 18 34 51 66 78 85]
[25 20 12 2 -9 -19 -27 -32] [-27 -22 -14 -4 7 17 25 30]
[-4 -6 -9 -13 -17 -20 -23 -25] [-43 -41 -38 -34 -30 -27 -24 -22]
[-37 -35 -33 -29 -25 -21 -18 -17] [-35 -36 -39 -43 -47 -51 -53 -55]
[-67 -63 -55 -44 -33 -22 -14 -10] [-5 -9 -17 -28 -39 -50 -58 -62]
[-90 -84 -71 -56 -39 -23 - 11 -4] [32 26 14 -1 -1 -18 -34 -46 -53]
[-102 -95 -81 -62 -42 -23 -9 -1] [58 50 36 18 -2 -20 -34 -42 ]
And now ... a mini test!
What to do next?
R = Y + 1.402 * Cr
G = Y - 0.34414 * Cb - 0.71414 * Cr
B = Y + 1.772 * Cb
Do not forget to add 128 each. If the values fall outside the interval [0, 255], assign boundary values. The formula is simple, but also eats up a fraction of the processor time.
Here are the tables for the channels R, G, B for the left upper square 8x8 of our example:
255 248 194 148 169 215 255 255
255 238 172 115 130 178 255 255
255 208 127 59 64 112 208 255
255 223 143 74 77 120 211 255
237 192 133 83 85 118 184 222
177 161 146 132 145 162 201 217
56 73 101 126 144 147 147 141
0 17 76 126 153 146 127 108
231 185 117 72 67 113 171 217
229 175 95 39 28 76 139 189
254 192 100 31 15 63 131 185
255 207 115 46 28 71 134 185
255 241 175 125 112 145 193 230
226 210 187 173 172 189 209 225
149 166 191 216 229 232 225 220
72 110 166 216 238 231 206 186
255 255 249 203 178 224 255 255
255 255 226 170 140 187 224 255
255 255 192 123 91 138 184 238
255 255 208 139 103 146 188 239
255 255 202 152 128 161 194 232
255 244 215 200 188 205 210 227
108 125 148 172 182 184 172 167
31 69 122 172 191 183 153 134
In general, I'm not a specialist in JPEG, so I can hardly answer all the questions. Just when I wrote my decoder, I often had to deal with various obscure problems. And when the image was displayed incorrectly, I did not know where I made a mistake. It may have misinterpreted bits, or it may have misused DCT. I really didn’t have a step-by-step example, so I hope this article will help when writing a decoder. I think it covers the description of the basic method, but all the same it is impossible to do just for it. I offer you the links that helped me:
ru.wikipedia.org/JPEG - for a superficial acquaintance.
en.wikipedia.org/JPEG is a much more comprehensive article on encoding / decoding processes.
JPEG Standard (JPEG ISO / IEC 10918-1 ITU-T Recommendation T.81)- Do not do without the 186-page specification. But there is no reason to panic - three quarters are occupied by flowcharts and applications.
impulseadventure.com/photo - Good detailed articles. For examples, I figured out how to build Huffman trees and use them when reading the appropriate section.
JPEGsnoop - On the same site there is an excellent utility that pulls out all the information of a jpeg file.
[FF D9]
[FF D8]
Have you ever wanted to know how a jpg file works? Now let's figure it out! Warm up your favorite compiler and hex editor, we will decode it:

Specially took a smaller picture. This is Google’s familiar but tightly squeezed favicon: I

warn you right away that the description is simplified and the information given is not complete, but then it will be easy to understand the specification.
Even without knowing how encoding occurs, we can already extract something from the file.
[FF D8]- start marker. It is always at the beginning of all jpg files.
Following are the bytes [FF FE] . This is a marker indicating the beginning of a comment section. The next 2 bytes [00 04] are the length of the section (including these 2 bytes). So in the next two [3A 29] - the comment itself. These are the character codes ":" and ")", i.e. regular emoticon. You can see it in the first line of the right side of the hex editor.
Bit of theory
Very briefly on the steps:
- Typically, an image is converted from an RGB color space to YCbCr .
- Often the channels Cb and Cr are thinned out, that is, an average value is assigned to the pixel block. For example, after thinning 2 times vertically and horizontally, the pixels will have this correspondence:

- Then the channel values are divided into 8x8 blocks (everyone saw these squares on an overly compressed image).
- Each block undergoes a discrete cosine transform (DCT) , which is a type of discrete Fourier transform . We get an 8x8 coefficient matrix. Moreover, the upper left coefficient is called the DC coefficient (it is the most important and is the average value of all values), and the remaining 63 are called AC coefficients.
- The resulting coefficients are quantized, i.e. each is multiplied by the coefficient of the quantization matrix (each encoder usually uses its own quantization matrix).
- They are then encoded with Huffman codes .

I remind you that each block Y ij , Cb ij , Cr ij is a matrix of DCT coefficients encoded by Huffman codes. In the file they are arranged in the following order:
Read file
After we have extracted the comment, it will be easy to understand that:
- The file is divided into sectors preceded by markers.
- Tokens are 2 bytes long, with the first byte [FF].
- Almost all sectors store their length in the next 2 bytes after the token.
FF D8 FF FE 00 04 3A 29 FF DB 00 43 00 A0 6E 78
8C 78 64 A0 8C 82 8C B4 AA A0 BE F0 FF FF F0 DC
DC F0 FF FF FF FF FF FF FF FF FF FF FF FF FF FF
FF FF FF FF FF FF FF FF FF FF FF FF FF FF FF FF
FF FF FF FF FF FF FF FF FF FF FF FF FF DB 00
43 01 AA B4 B4 F0 D2 F0 FF FF FF FF FF FF FF FF
FF FF FF FF FF FF FF FF FF FF FF FF FF FF FF FF
FF FF FF FF FF FF FF FF FF FF
FF FF FF FF FF FF FF FF FF FF FF FF FF FF FF FF
FF FF FF C0 00 11 08 00 10 00 10 03 01 22 00 02
11 01 03 11 01 FF C4 00 15 00 01 01 00 00 00 00
00 00 00 00 00 00 00 00 00 00 00 03 02 FF C4 00 1A
10 01 00 02 03 01 00 00 00 00 00 00 00 00 00 00 00
00 01 00 12 02 11 31 21 FF C4 00 15 01 01 01 00 00
00 00 00 00 00 00 00 00 00 00 00 00 00 00 01 FF
C4 00 16 11 01 01 01 00 00 00 00 00 00 00 00 00
00 00 00 00 00 11 00 01 FF DA 00 0C 03 01 00 02 11
03 11 00 3F 00 AE E7 61 F2 1B D5 22 85 5D 04 3C
82 C8 48 B1 DC BF FF D9
Marker [FF DB]: DQT - quantization table.
FF DB 00 43 00 A0 6E 78
8C 78 64 A0 8C 82 8C B4 AA A0 BE F0 FF FF F0 DC
DC F0 FF FF FF FF FF FF FF FF FF FF FF FF FF
FF FF FF FF FF FF FF FF FF FF FF FF FF FF FF FF
FF FF FF FF FF FF FF FF FF FF FF FF FF
The section header always takes 3 bytes. In our case, it is [00 43 00]. The header consists of:
[00 43] Length: 0x43 = 67 bytes
[0_] Length of the values in the table: 0 (0 - 1 byte, 1 - 2 bytes)
[_0] Table ID: 0
The remaining 64 bytes need to be filled in the 8x8 table .
[A0 6E 64 A0 F0 FF FF FF]
[78 78 8C BE FF FF FF FF]
[8C 82 A0 F0 FF FF FF FF]
[8C AA DC FF FF FF FF FF]
[B4 DC FF FF FF FF FF FF]
[F0 FF FF FF FF FF FF FF]
[FF FF FF FF FF FF FF FF]
[FF FF FF FF FF FF FF FF]
Take a look at the order in which the values in the table are filled. This order is called the zigzag order:

Marker [FF C0]: SOF0 - Baseline DCT
This marker is called SOF0, and means that the image is encoded using the basic method. It is very common. But on the Internet, the progressive method you are familiar with is no less popular when you first download a low-resolution image, and then a normal picture. This allows you to understand what is shown there, without waiting for a full download. The specification defines a few more, it seems to me, not very common methods.
FF C0 00 11 08 00 10 00 10 03 01 22 00 02
11 01 03 11 01
[00 11] Length: 17 bytes.
[08] Precision: 8 bits. The base method is always 8. As I understand it, this is the bit depth of the channel values.
[00 10] Pattern height: 0x10 = 16
[00 10] Pattern width: 0x10 = 16
[03] Number of components: 3. Most often it is Y, Cb, Cr.
1st component:
[01] Identifier: 1
[2_] Horizontal decimation (H 1 ): 2
[_2] Vertical decimation (V 1 ): 2
[00] Quantization table identifier: 0
2nd component:
[02] Identifier : 2
[1_] Horizontal decimation (H 2 ): 1
[_1] Vertical decimation (V 2 ): 1
[01] Quantization table identifier: 1
3rd component:
[03] Identifier: 3
[1_] Horizontal decimation (H3 ): 1
[_1] Vertical decimation (V 3 ): 1
[01] Quantization table identifier: 1
Now look at how to determine how thin the image is. We find
Marker [FF C4]: DHT (Huffman table)
This section stores codes and values obtained by Huffman coding .
FF C4 00 15 00 01 01 00 00 00 00
00 00 00 00 00 00 00 00 00 00 03 02
[00 15] Length: 21 bytes.
[0_] class: 0 (0 - table of DC coefficients, 1 - table of AC coefficients).
[_0] table identifier: 0
Huffman code length: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
Number of codes: [01 01 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00]
Number of codes means the number of codes of this length. Please note that the section stores only the code lengths, not the codes themselves. We must find the codes ourselves. So, we have one code of length 1 and one of length 2. Total 2 codes, there are no more codes in this table.
Each code has a value associated with it; they are listed next in the file. The values are single-byte, so we read 2 bytes.
[03] - the value of the 1st code.
[02] - the value of the 2nd code.
Further in the file you can see 3 more markers [FF C4], I will skip the analysis of the corresponding sections, it is similar to the above.
Building a Huffman Code Tree
We need to build a binary tree from the table we got in the DHT section. And already on this tree we recognize each code. We add the values in the order shown in the table. The algorithm is simple: no matter what node we are in, we always try to add a value to the left branch. And if she is busy, then to the right. And if there is no place there, then we return to a level higher and try from there. You need to stop at a level equal to the length of the code. Left branches correspond to the
Note:
You do not have to start from the top every time. Added value - return to the level above. Does the right branch exist? If so, go up again. If not, create the right branch and go there. Then, from this point, start your search to add the next value.
The trees for all the tables in this example are:

UPD (thanks anarsoul ): The nodes of the first tree (DC, id = 0) should have the values 0x03 and 0x02.
In the circles are the code values, under the circles are the codes themselves (I will explain that we got them by going through path from the top to each node). It is with these codes (this and other tables) that the very content of the picture is encoded.
Marker [FF DA]: SOS (Start of Scan)
Byte [DA] in the marker means - “YES! Finally, we went directly to parsing the encoded image section! ” However, the section is symbolically called SOS.
FF DA 00 0C 03 01 00 02 11
03 11 00 3F 00
[00 0C] The length of the header part (and not the entire section): 12 bytes.
[03] Number of scan components. We have 3, one per Y, Cb, Cr.
1st component:
[01] Image component number: 1 (Y)
[0_] Huffman table identifier for AC coefficients: 0
[_0] Huffman table identifier for AC coefficients: 0
2nd component:
[02] Image component number: 2 (Cb)
[1_]Huffman table identifier for DC coefficients: 1
[_1] Huffman table identifier for AC coefficients: 1
3rd component:
[03] Image component number: 3 (Cr)
[1_] Huffman table identifier for DC coefficients: 1
[_1] Identifier Huffman tables for AC coefficients: 1
These components cyclically alternate.
[00], [3F], [00] These bytes can be read in the specification.
This ends the header part, from here to the end (marker [FF D9]) encoded data.
[AE] [E7] [61] [F2] [1B]
101011101110011101100001111100100
Finding a DC coefficient.
1.We read the sequence of bits (if we meet 2 bytes [FF 00], then this is not a marker, but just a byte [FF]) . After each bit, we move along the Huffman tree (with the corresponding identifier) along the 0 or 1 branch, depending on the read bit. We stop if we are in the final node.
101011101110011101100001111100100
2. Take the value of the node. If it is 0, then the coefficient is 0, write to the table and go on to reading other coefficients. In our case - 02. This value is the length of the coefficient in bits. That is, we read the next 2 bits, this will be the coefficient.
101011101110011101100001111100100
3. If the first digit of the value in binary representation is 1, then leave it as it is: DC_coef = value. Otherwise, we transform:
Finding AC coefficients.
1. Similar to paragraph 1, finding the DC coefficient. We continue to read the sequence:
101011101110011101100001111100100
2. We take the value of the node. If it is 0, this means that the remaining matrix values must be filled with zeros. The next matrix is encoded further. The first few who read up to this place and wrote about it to me in PM will receive a plus in karma. In our case, the value of the node: 0x31.
First nibble: 0x3 - this is how many zeros we need to add to the matrix. These are 3 zero coefficients.
Second nibble: 0x1 - coefficient length in bits. Read the next bit.
101011101110011101100001111100100
3. Similar to item 3 of finding the DC coefficient.
As you already understood, you need to read AC-coefficients until we come across a zero value of the code, or until the matrix is filled.
In our case, we get:
101011101110011101100001111100100
and the matrix:
[2 0 3 0 0 0 0 0]
[0 1 2 0 0 0 0 0]
[0 -1 -1 0 0 0 0 0]
[1 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0]
You noticed that the values are filled in same zigzag pattern?
The reason for using this order is simple - since the larger the values of v and u, the less significant is the coefficient S vu in the discrete cosine transform. Therefore, at high compression ratios, unimportant coefficients are reset to zero, thereby reducing the file size.
Similarly, we get 3 more Y-channel matrices ...
[-4 1 1 1 0 0 0 0] [5 -1 1 0 0 0 0 0]
[0 0 1 0 0 0 0 0] [-1 -2 -1 0 0 0 0 0]
[0 -1 0 0 0 0 0 0] [0 -1 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0] [-1 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0] [0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0] [0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0] [0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0] [0 0 0 0 0 0 0 0]
[-4 2 2 1 0 0 0 0]
[-1 0 -1 0 0 0 0 0]
[-1 -1 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0 0]
Oh, I forgot to say that the encoded DC coefficients are not the DC coefficients themselves, but their differences between the coefficients of the previous table (the same channel)! You need to correct the matrix:
DC for the 2nd: 2 + (-4) = -2
DC for the 3rd: -2 + 5 = 3
DC for the 4th: 3 + (-4) = -1
[-2 1 1 1 0 0 0 0] [3 -1 1 0 0 0 0 0] [-1 2 2 1 0 0 0 0]
...........
Now the order. This rule is valid until the end of the file.
... and according to the matrix for Cb and Cr:
[-1 0 0 0 0 0 0 0] [0 0 0 0 0 0 0 0]
[1 1 0 0 0 0 0 0] [1 -1 0 0 0 0 0 0 ]
[0 0 0 0 0 0 0 0] [1 0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0] [0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0] [0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0] [0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0] [0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0] [0 0 0 0 0 0 0 0]
Since there is only one matrix, DC coefficients can not be touched.
Calculations
Quantization
Do you remember that the matrix goes through the quantization stage? The elements of the matrix must be multiplied termwise with the elements of the quantization matrix. It remains to choose the right one. First, we scanned the first component, its image component = 1. The image component with this identifier uses the quantization matrix 0 (we have the first of two). So, after the multiplication:
[320 0 300 0 0 0 0 0]
[0 120 280 0 0 0 0 0]
[0 -130 -160 0 0 0 0 0]
[140 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0]
Similarly, we get 3 more Y-channel matrices ...
[-320 110 100 160 0 0 0 0] [480 -110 100 0 0 0 0 0]
[0 0 140 0 0 0 0 0] [-120 -240 -140 0 0 0 0 0]
[0 -130 0 0 0 0 0 0] [0 -130 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0 0] [-140 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0] [0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0] [0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0] [0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0] [0 0 0 0 0 0 0 0 0]
[-160 220 200 160 0 0 0 0]
[-120 0 -140 0 0 0 0 0]
[-140 - 130 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0]
... and in the matrix for Cb and Cr.
[-170 0 0 0 0 0 0 0] [0 0 0 0 0 0 0 0 0]
[180 210 0 0 0 0 0 0] [180 -210 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0] [240 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0] [0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0] [0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0] [0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0] [0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0 0] [0 0 0 0 0 0 0 0 0]
Inverse Discrete Cosine Transformation
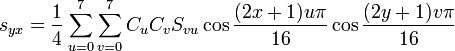

The formula should not be difficult *. S vu is our obtained matrix of coefficients. u is a column, v is a row. s yx are the channel values themselves.
* Generally speaking, this is not entirely true. When I was able to decode and display a 16x16 picture, I took a 600x600 image (by the way, it was the cover of my favorite Mind.In.A.Box album - Lost Alone). It didn’t work right away - various bugs surfaced. Soon I could admire the correctly uploaded picture. Only very upset the download speed. I still remember, it took 7 seconds. But this is not surprising, if you use the above formula thoughtlessly, then to calculate one channel of one pixel, you will need to find 128 cosines, 768 multiplications, and some additions there. Just think about it - almost a thousand difficult operations on only one channel of one pixel! Fortunately, there is scope for otimization (after long experiments, I reduced the load time to a timer accuracy limit of 15ms, and after that changed the image to a photograph 25 times larger. Perhaps I will write about this in a separate article).
I will write the result of calculating only the first matrix of channel Y (the values are rounded):
[138 92 27 -17 -17 28 93 139]
[136 82 5 -51 -55 -8 61 111]
[143 80 -9 -77 -89 -41 32 86]
[157 95 6 -62 -76 -33 36 86]
[147 103 37 -12 -21 11 62 100]
[87 72 50 36 37 55 79 95]
[-10 5 31 56 71 73 68 62]
[- 87 -50 6 56 79 72 48 29]
and the two remaining:
Cb Cr
[60 52 38 20 0 -18 -32 -40] [19 27 41 60 80 99 113 120]
[48 41 29 13 -3 -19 -31 -37] [0 6 18 34 51 66 78 85]
[25 20 12 2 -9 -19 -27 -32] [-27 -22 -14 -4 7 17 25 30]
[-4 -6 -9 -13 -17 -20 -23 -25] [-43 -41 -38 -34 -30 -27 -24 -22]
[-37 -35 -33 -29 -25 -21 -18 -17] [-35 -36 -39 -43 -47 -51 -53 -55]
[-67 -63 -55 -44 -33 -22 -14 -10] [-5 -9 -17 -28 -39 -50 -58 -62]
[-90 -84 -71 -56 -39 -23 - 11 -4] [32 26 14 -1 -1 -18 -34 -46 -53]
[-102 -95 -81 -62 -42 -23 -9 -1] [58 50 36 18 -2 -20 -34 -42 ]
And now ... a mini test!
What to do next?
- Oh, let’s go eat!
- Yes, I don’t enter what I mean.
- Once the values of YCbCr colors are obtained, it remains to convert to RGB, such as:
YCbCrToRGB (Y ij , Cb ij , Cr ij ) , Y ij , Cb ij , Cr ij are our obtained matrices. - 4 matrices Y, and one Cb and Cr each, since we thinned out the channels and 4 pixels Y corresponds to one Cb and Cr each. Therefore, calculate this:
YCbCrToRGB (Y ij , Cb [i / 2] [j / 2] , Cr [i / 2] [j / 2] )
YCbCr to RGB
R = Y + 1.402 * Cr
G = Y - 0.34414 * Cb - 0.71414 * Cr
B = Y + 1.772 * Cb
Do not forget to add 128 each. If the values fall outside the interval [0, 255], assign boundary values. The formula is simple, but also eats up a fraction of the processor time.
Here are the tables for the channels R, G, B for the left upper square 8x8 of our example:
255 248 194 148 169 215 255 255
255 238 172 115 130 178 255 255
255 208 127 59 64 112 208 255
255 223 143 74 77 120 211 255
237 192 133 83 85 118 184 222
177 161 146 132 145 162 201 217
56 73 101 126 144 147 147 141
0 17 76 126 153 146 127 108
231 185 117 72 67 113 171 217
229 175 95 39 28 76 139 189
254 192 100 31 15 63 131 185
255 207 115 46 28 71 134 185
255 241 175 125 112 145 193 230
226 210 187 173 172 189 209 225
149 166 191 216 229 232 225 220
72 110 166 216 238 231 206 186
255 255 249 203 178 224 255 255
255 255 226 170 140 187 224 255
255 255 192 123 91 138 184 238
255 255 208 139 103 146 188 239
255 255 202 152 128 161 194 232
255 244 215 200 188 205 210 227
108 125 148 172 182 184 172 167
31 69 122 172 191 183 153 134
the end
In general, I'm not a specialist in JPEG, so I can hardly answer all the questions. Just when I wrote my decoder, I often had to deal with various obscure problems. And when the image was displayed incorrectly, I did not know where I made a mistake. It may have misinterpreted bits, or it may have misused DCT. I really didn’t have a step-by-step example, so I hope this article will help when writing a decoder. I think it covers the description of the basic method, but all the same it is impossible to do just for it. I offer you the links that helped me:
ru.wikipedia.org/JPEG - for a superficial acquaintance.
en.wikipedia.org/JPEG is a much more comprehensive article on encoding / decoding processes.
JPEG Standard (JPEG ISO / IEC 10918-1 ITU-T Recommendation T.81)- Do not do without the 186-page specification. But there is no reason to panic - three quarters are occupied by flowcharts and applications.
impulseadventure.com/photo - Good detailed articles. For examples, I figured out how to build Huffman trees and use them when reading the appropriate section.
JPEGsnoop - On the same site there is an excellent utility that pulls out all the information of a jpeg file.
[FF D9]
