Methods for applying the algorithm for finding the maximum flow in the network

Introduction

The maximum flow problem is classical and has many applications. Let me remind you the problem statement. A weighted directed graph with non-negative weights (throughputs) is given. Obtained two peaks: the source S and drain T such that every other vertex lies on the path from S to T . A flow is a function F: V x V with such properties

1. Bandwidth Limit. Flow along an edge cannot be greater than its (edge) throughput.
2. Antisymmetry. For each edge (u, v): F (u, v) = -F (v, u).
3. Saving stream. For each vertex (except S and T ), the amount of incoming stream (negative) is equal to the number of outgoing stream (positive). That is, the algebraic sum of the flows for each vertex (except for S and T ) is equal to zero.

In this post you can familiarize yourself with the implementation of the problem.

We proceed directly to typical tasks, which are reduced to an algorithm for finding the maximum flow in the network. Often it is very difficult to identify the flow in such tasks.

Tasks

1. The problem of maximum matching. At the entrance is given N - the number of boys, M - the number of girls and a list of which boy with which of the girls wants to dance (there may be several). It is necessary to determine the maximum number of simultaneously dancing couples.
   
   
   

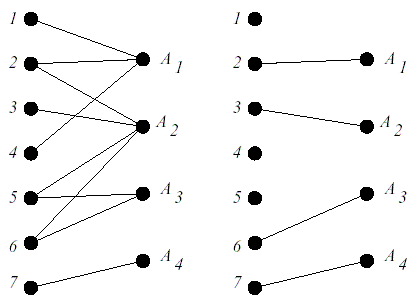
   Decision

   
   To solve this problem, you can use the Kuhn algorithm , but since we started to reduce everything to a stream - let's do it. There is not enough source and drain for this. Let's add them! “On the left” we add a fictitious vertex and draw ribs to all the boys weighing 1. From boys to girls there are ribs and put them the same price 1. And from girls ribs to the drain also cost 1. The answer to the problem is the maximum flow between the source and drain .
2. Damaged parquet. At NxM Parquet, some cells may be damaged. They must be covered with new tiles. Tiles are 2x1 in size (you can rotate, but cannot be cut) at a price of A, and 1x1 at a price of B. The question is, what is the minimum amount you need to spend to lay damaged floor tiles. Naturally, new tiles should not overlap any other tiles.
   
   

   Decision

   
   First, make sure that 2 * B> A. Otherwise, it is more profitable to tile only 1x1 tiles and there is nothing more to consider. Further, our task is to maximize the number of tiles at the price of A. We
   paint our parquet on the principle of a chessboard. Obviously, then one end of the 2x1 tile will lie on the black cage, the other on the white. So, we will build a bipartite graph, one share of which will contain white cells, the other - black ones. We will draw ribs weighing 1 between the adjacent cells. Add a source with edges to white peaks weighing at infinity (a fairly common trick) and a drain with edges from black cells weighing at infinity too. Let f be the value of the maximum flow found between the source and the drain. That is, we found the number of tiles 2x1. The answer to the problem is f * A + (Kf) * B, where K is the total number of damaged cells.
   Source: Kharkov Winter Programming School, 2009, Day 3
   
3. The task of painting. Given an N * M matrix with cells painted either black or white. W is the price of repainting a black square in white, B - white in black. After repainting, between all adjacent squares of different colors, you need to draw a gray line, at the price of G. You need to repaint the matrix so fast (or do nothing) in order to spend the minimum amount.
   
   
   

   Decision

   
   Extreme case: if the matrix is ​​all of the same color, the answer is 0.
   Add a fictitious source and drain. From the source to all the white peaks we draw the edges weighing in B (the price of repainting to black). From the black peaks to the drain we draw ribs weighing in W (the price of repainting to white). And between all neighboring vertices (whether they are of the same or different colors) - we put an edge weighing in G (gray line). The magnitude of the maximum flow will be the answer to the problem.
   Source: All-Ukrainian School Olympiad in Informatics, 2007, Day 1
   
4. Problem with constraint on tops. Let it be necessary to find the magnitude of the maximum flow and the peaks have a limit on how much they can miss.
   
   

   Decision

   
   All we need is to divide each vertex into two, and put an edge between them, weighing in the bandwidth limit of this vertex
5. Minimum cut. Dan Count. How many vertices must be removed so that there is no path from A to B?
   
   

   Decision

   
   In the classical minimal cut problem, edges must be removed. Not a problem! We divide the vertices into 2, and put an edge between them, weighing 1. Then the answer to the problem is to find the minimum cut in the graph (which is the maximum flow).
   Source: Kharkov Winter Programming School, 2009, Day 3
   
6. The writer of verses. There is a deterministic finite state machine with one initial state A and one final B. Each transition is defined by a triple of numbers (i, j, k), a transition from state i to state j along edge k.
   After passing through the automaton from i to j along the edge k, all transitions from i along the edge k are erased, as well as all transitions to j along the edge k. It is required to deduce the number of paths from A to B by such an automaton.
   
   

   Decision

   
   The task is to find the maximum number of paths, and more than one edge of the same color does not go out from one vertex. We reduce the problem to finding the maximum flow. For each vertex, create k + 1 vertex in the rebuilt network. The first vertex will be the input, the remaining vertices will represent the colors. From the top of the entrance, draw an edge with a throughput of 1 to each of the k vertices corresponding to the color. From the vertex corresponding to color i, we draw all the edges of color i into the inputs of the ends of the edges. Having found the maximum flow in such a network, we obtain the maximum number of paths satisfying the required property.
   Source: Kharkov Winter Programming School, 2009, Day 4
   
7. Collecting coins. There are n collectors and m types of coins. To join the club, you must have at least one coin of each type. You (you have number 1) can exchange available coins with collectors. Any collector will exchange his coin a for your coin b if he has more than one coin of type a and does not have a single coin of type b . You, in turn, may violate this rule. You need to collect as many types of coins as possible from the known situation of all collectors.
   
   

   Decision

   
   Build a network. For each type of coin, create one vertex. These tops will match your coins. It is necessary to collect as many unique coins as possible, so draw a bandwidth edge 1 into the drain from each such vertex. To the vertices corresponding to the coins that you initially have, draw an edge whose throughput is equal to the number of such coins you have.
   For each member of the club (except for 1, that is, you) we have one vertex. This vertex can take no more than one coin, which it does not have, and give
   no more than k-1 coins, of which it has k (k> 1). Naturally, a member of the club gives one coin in return for one received.
   Thus, at each such vertex, you need to draw a bandwidth edge 1 of the vertices corresponding to the coins that this club member does not have. And from these vertices, it is necessary to draw ribs with a throughput capacity k _i - 1 to the vertex i corresponding to the coins, which the club member has more than one.
   The constructed network reflects the exchange processes in the club. The maximum flow in such a network will be equal to the maximum number of coins that can be collected by you.
   Source: Kharkov Winter Programming School, 2009, Day 4
   
8. Circulation. The reactor cooling system is a set of pipes connecting the nodes. Liquid flows through the pipes, and for each pipe, the direction in which it should flow through it is strictly defined. The nodes of the cooling system are numbered from 1 to N. The cooling system must be designed so that for each node for a unit of time the amount of liquid flowing into the node is equal to the amount of liquid flowing from the node. Each pipe has a throughput c _ij . In addition, to ensure sufficient cooling, it is required that at least l _ij units of fluid per unit time flow through the pipe . That is, for a pipe leading from the ith node to the jth node, l _ij ≤ f _ij ≤ c _ij.
   The description of the cooling system is given. It is necessary to find out how to let the liquid flow through the pipes so that all of the indicated conditions are met.
   
   

   Decision

   
   This is the problem of finding circulation in a network with given lower restrictions on the edges. If a stream in the segment [l, r] should pass along the edge (u, v), then in the rebuilt network there will be three edges (where, where, weight): (u, v, r - l), (S, v, l ), (u, T, l). S, T - additionally entered drain and source, respectively. In fact, we pass the required minimum flow along the edge, and then balance it so that we get circulation.
   Source: Kharkov Winter Programming School, 2009, Day 4
   
9. Dancing again. N boys and n girls are invited to the party. They want to dance a few rounds.
   In each round, guests are divided into n dancing couples. Each guest should be in some pair, each pair should consist of one boy and one girl. In each round, each boy must dance with a different girl. Some boys and girls do not like each other. Each boy can dance with no more than k girls that he does not like. Similarly, each girl can dance with no more than k boys that she does not like.
   There is information about whether the i-th boy and the j-th girl (1 ≤ i, j ≤ n) like each other. Find the largest number of rounds that you can dance at a party.
   
   

   Decision

   
   Consider the following problem: can dancing continue in exactly m rounds? If we can answer this question, then by binary search we find the largest m for which dancing is possible.
   We construct a graph having one source and one sink (black vertices). Red peaks represent boys, gray peaks represent girls. If the boy and the girl like each other, then we draw between them an edge of unit capacity (in the figure, these are two edges - the upper and the lower). Otherwise, add the blue and green vertices as shown in the figure and set the bandwidth of the edges between the corresponding blue and green vertices to 1.
   Blue and green peaks form a “protective” level. The connection of boys with girls who do not like each other will go along the edges of the protective level. Each boy can dance with no more than k girls that he does not like. Set the bandwidth of the edges between the red and blue, green and gray peaks equal to k. Thus, between each boy and each girl, a connection will be established through the edge either directly or through the peaks of the protective level.
   Dancing must continue in exactly m rounds. Set the bandwidth of the edges between the source and the red peaks, as well as between the gray peaks and the drain, equal to m.
   
   Find the maximum flow in the graph. Dancing can continue in exactly m rounds if and only if the maximum flow is equal to n * m, where n is the number of boys.
   Source: Sevastopol Summer Programming School, 2010, Day 4
   

Conclusion

We examined a negligible part of the immense set of tasks that boil down to finding the maximum flow in the network. And this is not affecting the maximum flow of minimum cost. Such tasks are distinguished by their beauty in solving. The programmer, knowing the standard algorithm for finding the maximum flow, can only build a graph corresponding to the task and start the flow.