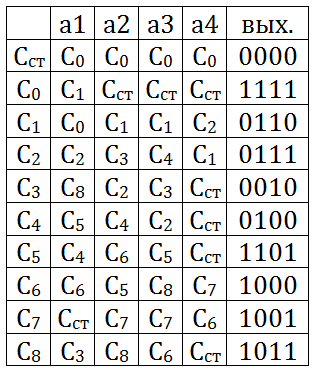Independent study of circuitry. Synthesis of automata on triggers. Part 1
Hello.
In continuation of the topic of independent study of circuitry, I bring to your attention an article related to the synthesis of automata on triggers.
And it all starts like this: “The peasant needs to transport the wolf, goat and cabbage across the river. But the boat is such that only a peasant can fit in it, and with it either one wolf, or one goat, or one cabbage. But if you leave the wolf with the goat, then the wolf will eat the goat, and if you leave the goat with cabbage, the goat will eat cabbage. How did the peasant transport his cargo? ” We digress a little from the task and recall what we already know:

So. There are 2 ways to solve this problem:
To go from verbal descriptions of tables, graphs and diagrams, I propose to encode the state of the game as follows:
We distinguish four binary digits. Each category is responsible for what creatures on which bank of the river are. If 1 is stored in this category, then the creature is on the first (source) bank, if 0 is on the second. For clarity, I will demonstrate this in the following figure: From the conditions of the task it becomes clear that without the supervision of a peasant they cannot be together:

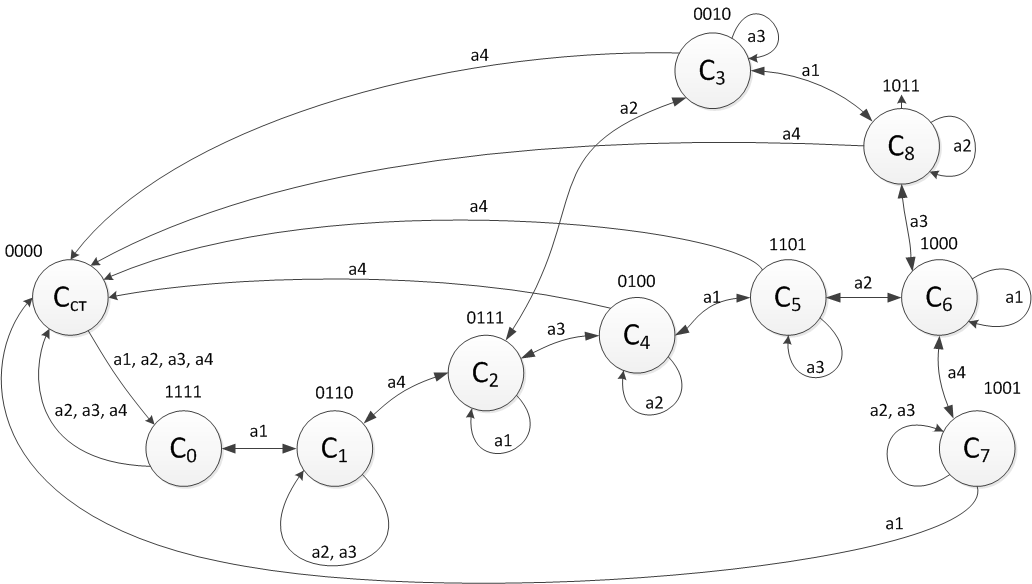
So, the following four combinations are losing: Now, as we all remember, we need to move from a verbal description to a graphical description - a graph. It should not be difficult. We note the initial state of CST - from it our game will begin and end with it. It is thought that a certain “START” button transfers the machine from state “0000” to state “1111”. Please note that this is how I code the output words, but the states will have to be encoded in a different way. So, you have to introduce a combinational circuit that will engage in the formation of output words. To control the peasant and other entities, four input words are needed:

So. Input and output words are named, states are indicated. Count of Moore's assault rifle. Let's start drawing:
We reflect these two facts on the graph: We argue further:
Add this to our picture: So far, everything is fine. Now you need to choose who to bring to the second bank: cabbage or wolf. It would be nice to consider both options (I will give the figure partially to make it easier to perceive): That is, it is clear that on the first bank after this movement either cabbage or a wolf will remain. Here you go! I said that it’s not difficult! If we continue the reasoning in the same vein, we can come to such a simple scheme: Note: when you try in 3, 4, 5 and 8 states of a peasant to go to the other side, the goat is left unattended next to the wolf or cabbage, which is fraught with leads to the end of the game. Well, or just look at the table of invalid states above. When you try to switch to them, the game ends.

Now remember how the transition / exit tables are built. I recommend to open this article here and see if you suddenly forgot, and I'll just give you a table: Well. Now almost everything is ready for the synthesis of the machine on the triggers. Very soon we will be able to play this toy on the emulator, and then on the assembled model. I intend to publish the second part of the article on June 14-15.
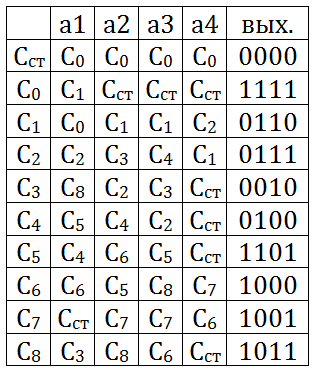
In continuation of the topic of independent study of circuitry, I bring to your attention an article related to the synthesis of automata on triggers.
And it all starts like this: “The peasant needs to transport the wolf, goat and cabbage across the river. But the boat is such that only a peasant can fit in it, and with it either one wolf, or one goat, or one cabbage. But if you leave the wolf with the goat, then the wolf will eat the goat, and if you leave the goat with cabbage, the goat will eat cabbage. How did the peasant transport his cargo? ” We digress a little from the task and recall what we already know:

So. There are 2 ways to solve this problem:
- We have to start with a goat. The peasant, having transported the goat, returns and takes the wolf, which he carries to the other side, where he leaves him, but then he takes and takes the goat back to the first bank. Here he leaves her and carries cabbage to the wolf. Then, after returning, he carries the goat, and the crossing ends safely.
- At first, the peasant again transported the goat. Then you can take the cabbage, take it to the other side, leave there and return the goat to the first shore. Then transport it to the other side of the wolf, return for the goat and again take it to the other side. In this case, the number of flights (7) is exactly the same as in the first embodiment.
To go from verbal descriptions of tables, graphs and diagrams, I propose to encode the state of the game as follows:
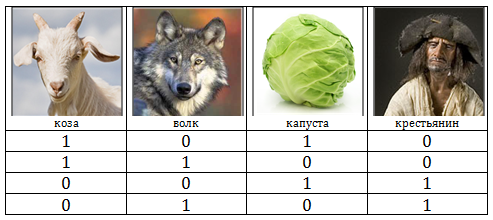
We distinguish four binary digits. Each category is responsible for what creatures on which bank of the river are. If 1 is stored in this category, then the creature is on the first (source) bank, if 0 is on the second. For clarity, I will demonstrate this in the following figure: From the conditions of the task it becomes clear that without the supervision of a peasant they cannot be together:

- Goat and cabbage;
- Goat and wolf.
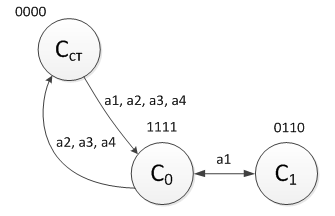
So, the following four combinations are losing: Now, as we all remember, we need to move from a verbal description to a graphical description - a graph. It should not be difficult. We note the initial state of CST - from it our game will begin and end with it. It is thought that a certain “START” button transfers the machine from state “0000” to state “1111”. Please note that this is how I code the output words, but the states will have to be encoded in a different way. So, you have to introduce a combinational circuit that will engage in the formation of output words. To control the peasant and other entities, four input words are needed:


So. Input and output words are named, states are indicated. Count of Moore's assault rifle. Let's start drawing:
- From the zero state, the game is transferred to the initial position upon the arrival of any word.
- Obviously, only when the peasant takes the goat first (A1) the game can be continued, otherwise (A2, A3, A4) will have to start all over again.
We reflect these two facts on the graph: We argue further:

- If you now apply the words a2 or a3 to the input, it is clear that the peasant will not be able to transport the wolf or cabbage, so the state of the game will not change. However, he can take the goat back and the game will return to its original state.
- So the only non-deadlock action will be the return of the peasant to the first shore.
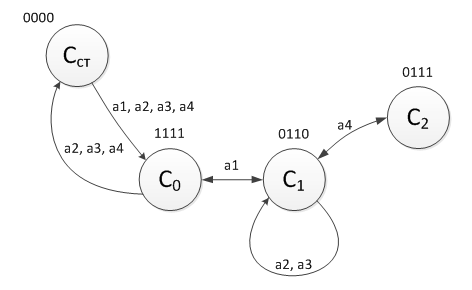
Add this to our picture: So far, everything is fine. Now you need to choose who to bring to the second bank: cabbage or wolf. It would be nice to consider both options (I will give the figure partially to make it easier to perceive): That is, it is clear that on the first bank after this movement either cabbage or a wolf will remain. Here you go! I said that it’s not difficult! If we continue the reasoning in the same vein, we can come to such a simple scheme: Note: when you try in 3, 4, 5 and 8 states of a peasant to go to the other side, the goat is left unattended next to the wolf or cabbage, which is fraught with leads to the end of the game. Well, or just look at the table of invalid states above. When you try to switch to them, the game ends.



Now remember how the transition / exit tables are built. I recommend to open this article here and see if you suddenly forgot, and I'll just give you a table: Well. Now almost everything is ready for the synthesis of the machine on the triggers. Very soon we will be able to play this toy on the emulator, and then on the assembled model. I intend to publish the second part of the article on June 14-15.