A challenge for five year olds that has become “viral”
- Transfer
The whole truth about the newest viral puzzle from Singapore and another historical riddle with numbers.

In honor of the anniversary of this column, the Internet kindly provided me with a Singaporean mathematical puzzle that had become viral . In mid-May, the web was agitated by a task that Singapore’s first-graders allegedly give to solve, and these are children aged 5 to 7 years old, and which turned out to be so complex that no one can solve it.

Carefully study the sequence of numbers and fill in the gaps.
But our story is really about how phrases like “math problem shook the Internet” became boring and predictable attempts to attract visitors to the page. Since even a brief look at this question, which first appeared on the Singapore Technical Forum , suggests that this photo is an obvious fake. The photo looks edited, but there is no explanation for the problem.
Apparently, the task was taken (and modified) from the site devoted to mathematical puzzles, which is led by Gordon Burgin, an American retired teacher. And in the version from the site in the left lower quarter the figure is 20. In Singapore photo 0 is smeared. No wonder there is no obvious solution!
“I am amazed by this fake and I don’t know what they were trying to achieve with this,” Burgin says. “If their goal was a heated discussion and subsequent despair, then they achieved their goal!”
Then comes the correct version of the riddle.
1. In each of the four sectors of the outer circle there is a two-digit number equal to the sum of the three numbers located in the corners of this sector. Numbers in individual circles can vary from 1 to 9, and each of the numbers can be used only once. One of the numbers given to you in order to start. Find the remaining four.
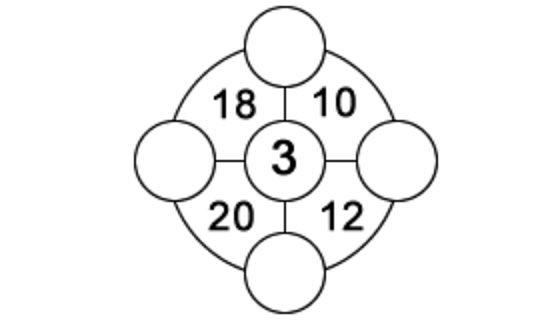
2. Since the Singapore riddle was wrong - try to propose a variant of the problem that would be suitable for the given picture (with overwritten zero).
This riddle reminded me of a puzzle from one of the most interesting books on the history of riddles: "Wakoku chiekurabe ", the oldest Japanese book of riddles, published in 1727. This is a great mystery - and, at least, it was born in the East!
3. Write numbers from 1 to 9 in black circles so that the sum of the numbers, located on each of the two blue circles (including the center circle), and also along the horizontal and vertical lines were the same.
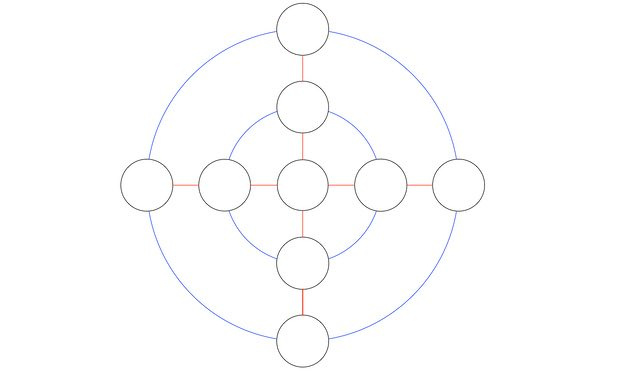
These are four sums, each of which consists of five terms, and all the sums are the same. similar task.


1. Clockwise, starting from the top: 6, 1, 8, 9
If we call the positions for the numbers North, East, West, and South, then the candidates for the West and the South are 8 and 9, since Yu + W + 3 = 20 or Yu + 3 = 17. But we know that Yu + B + 3 = 12, or Yu + B = 9. But Yu cannot be 9, because then B = 0, and this is forbidden. Therefore, = = 8, = 9, C = 6, and B = 1.
2. I liked most of all the assignment sent by the reader named Tom Flannery, because it turned out to be very simple.
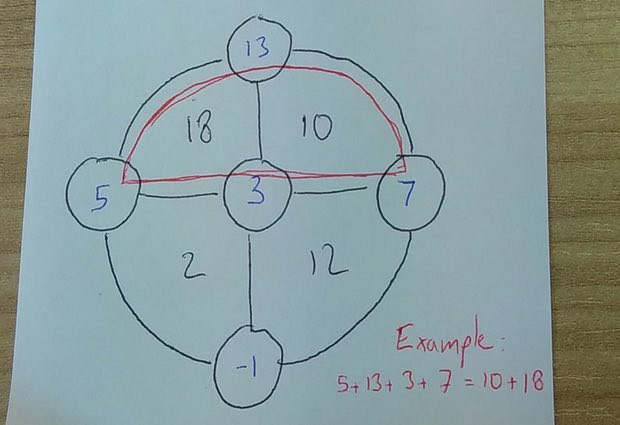
3. And the last task, from the Japanese book of riddles of 1727.
There may be many solutions. Here is my solution:
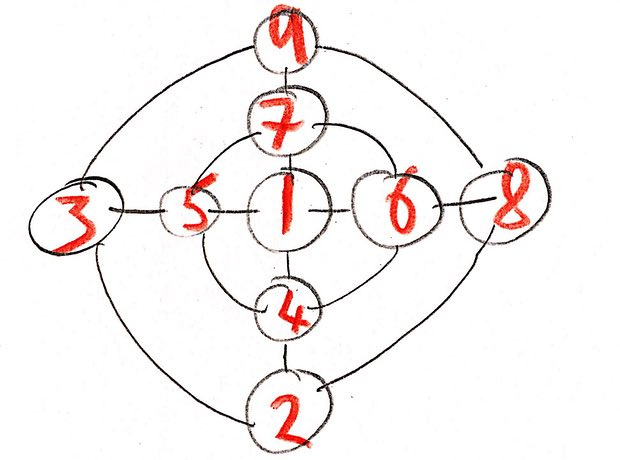
The way to the solution helps to build a guess - in the center there can be only an odd number. Having chosen such a number, it is necessary to divide the remaining digits into pairs, which together give the same number, and arrange them in opposite circles. I chose 1 for the center, respectively, there are pairs 2 and 9, 3 and 8, 4 and 7, 5 and 6 - they all add up to 11.

In honor of the anniversary of this column, the Internet kindly provided me with a Singaporean mathematical puzzle that had become viral . In mid-May, the web was agitated by a task that Singapore’s first-graders allegedly give to solve, and these are children aged 5 to 7 years old, and which turned out to be so complex that no one can solve it.

Carefully study the sequence of numbers and fill in the gaps.
But our story is really about how phrases like “math problem shook the Internet” became boring and predictable attempts to attract visitors to the page. Since even a brief look at this question, which first appeared on the Singapore Technical Forum , suggests that this photo is an obvious fake. The photo looks edited, but there is no explanation for the problem.
Apparently, the task was taken (and modified) from the site devoted to mathematical puzzles, which is led by Gordon Burgin, an American retired teacher. And in the version from the site in the left lower quarter the figure is 20. In Singapore photo 0 is smeared. No wonder there is no obvious solution!
“I am amazed by this fake and I don’t know what they were trying to achieve with this,” Burgin says. “If their goal was a heated discussion and subsequent despair, then they achieved their goal!”
Then comes the correct version of the riddle.
1. In each of the four sectors of the outer circle there is a two-digit number equal to the sum of the three numbers located in the corners of this sector. Numbers in individual circles can vary from 1 to 9, and each of the numbers can be used only once. One of the numbers given to you in order to start. Find the remaining four.

2. Since the Singapore riddle was wrong - try to propose a variant of the problem that would be suitable for the given picture (with overwritten zero).
This riddle reminded me of a puzzle from one of the most interesting books on the history of riddles: "Wakoku chiekurabe ", the oldest Japanese book of riddles, published in 1727. This is a great mystery - and, at least, it was born in the East!
3. Write numbers from 1 to 9 in black circles so that the sum of the numbers, located on each of the two blue circles (including the center circle), and also along the horizontal and vertical lines were the same.

These are four sums, each of which consists of five terms, and all the sums are the same. similar task.

Solutions

1. Clockwise, starting from the top: 6, 1, 8, 9
If we call the positions for the numbers North, East, West, and South, then the candidates for the West and the South are 8 and 9, since Yu + W + 3 = 20 or Yu + 3 = 17. But we know that Yu + B + 3 = 12, or Yu + B = 9. But Yu cannot be 9, because then B = 0, and this is forbidden. Therefore, = = 8, = 9, C = 6, and B = 1.
2. I liked most of all the assignment sent by the reader named Tom Flannery, because it turned out to be very simple.
Fill the circles with integers so that the sum of the sectors in each of the semicircles equals the sum of the numbers in the circles.

3. And the last task, from the Japanese book of riddles of 1727.
There may be many solutions. Here is my solution:

The way to the solution helps to build a guess - in the center there can be only an odd number. Having chosen such a number, it is necessary to divide the remaining digits into pairs, which together give the same number, and arrange them in opposite circles. I chose 1 for the center, respectively, there are pairs 2 and 9, 3 and 8, 4 and 7, 5 and 6 - they all add up to 11.
