Philosophical geometry. Part 4, Final. Golden ratio and root of five
Oh God, the fourth part! This is beyond my power! Calm, I'm running out of pills, so this is the last article, and there will be revelations in it. Under cat description of the process of fitting, retraction, entanglement and manipulation.
In the previous ( 1 , 2 , 3 ) parts, we saw how different proportions were used in geometry, ancient art, and modern industrial design. We still have an unsolved topic of the golden ratio and another root - √5. Let's start.
Once, people came across the idea of proportions. In different figures the same patterns were constantly met. It was impressive. Then someone thought of measuring a couple of plants, animals and some parts of the body that are usually hidden from strangers. Patterns were there. It was even more impressive.
There is no more urine left, the most common relationships have been declared sacred. Some saw in them a manifestation of divine intervention. Some are of God himself. And since sacred proportions are so often found, then you can fit whatever you want under them, make a symbol out of it and frighten the flock.
Hoaxes and postscripts from the best of intentions are found in history constantly. For example, the scribes of the classic work “Church History of the People of the Angles” of the Venerable Bad’s attached pieces to the text so that certain church questions would look more favorable. And 25-28 of chapter VI of the book "Notes on the Gallic War" by Caesar apparently not so Caesar.
The same is true in symbolism. It is necessary that people feel its deepest meaning, and the form itself is not so important. Take any picture, in it surely yes something will be found. The older the better. Our oldest Egypt, exercise on it.
Here is a bas-relief diagram of the tomb of Petosiris, found in 1919.

After sitting enough time with a ruler and compass, you can find in it a golden ratio and a bunch of different relationships (besides text letters, wits, you don't need a compass for this).
It looks pretty cool, so there is no reason not to say that the Egyptians knew about the Golden Ratio and did it on purpose.
Mystifying geometry is easy and simple. Now I will show you a couple of tricks. Look under the cat.
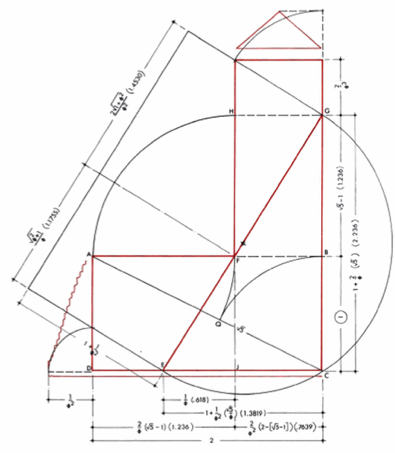
So, the tricks. Well, firstly, all these proportions are so ancient that all the coolest constructions are well described. Having opened the directory, we see how to simulate the very golden proportions in the simplest way. We take a square, draw end-to-end the same and draw the diagonal AC.

With a center O and a radius OA, we draw a circle. Extend the FE line to the point of intersection with the circle K. Then you can repeat the focus with the circle for side AB, but it is easier to draw the perpendicular KH from K, extend AB and mark the intersection point of H.

Voila, we get a “golden rectangle”. The ratio of FE to EK is the same as FK to FE. Even more awesome, KF / FB also equals this. For brevity, the Greeks called this relation φ (Phi). It is approximately equal to 1.618 We
show creativity and make a couple more passes. Connect the corners of the original square and the resulting rectangle. Let's draw a circle on the formed points.
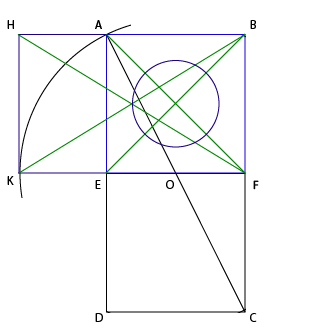
Now, to open the veil of great mystery, we need to find something to fit into this rectangle. Remembering how lucky we were with Apple, let's go the simplest way and make the obvious.
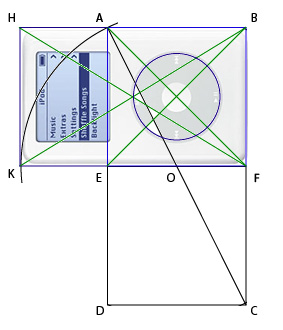
Hurrah! We managed to declare the iPod 4G a sacred device. It is obvious that now they will definitely buy it.
Here it is - the benefit of studying textbooks. Geometry has existed for so long that it costs nothing to take reference books, and classical sources, write books and earn a lot of profit on it.
You look, the book is being filmed with an actor of a form that has gone awry from the script, and the profit will be an order of magnitude more. You can compost the reader’s brain, or you can compost the reader’s brain by how you can compost the reader’s brain - also, by the way, profitable (well, you know what I mean, my well-read commentators). To the extreme, you can hit contemporaries and earn some advantages by solving the secrets of the Arabian mosaic, linking it ... well, let's say with a bee.
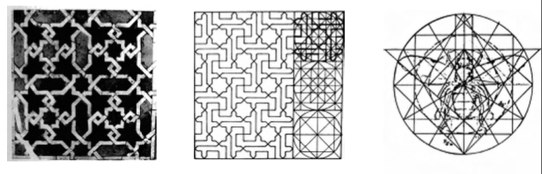
In fact, in art, of course, it is all about ordinary modular grids and guide lines that artists and designers use to compose compositions. The idea is so old that even the oldest of the ancient Egyptians used it.

Compositions are taught in art schools, and those who also teach someone once taught. So no mystery. Unless only the very first teacher invented something there. The rest is enough to take some kind of grid and place elements on it.
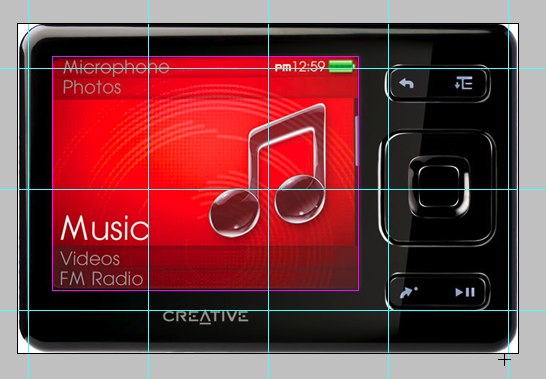
But the one and a half aspect ratio and square modules are not interesting. There is no secret. It’s better to take something more sacred. Let's say one more known relation is √5. The Zune player is just that.

Let's look at the directory and see what patterns may come up.
We put them on the player. Hm. There is nothing similar yet. Let's try to sort through all the options.

Ummm ... It's somehow rotten. Only touches near the central button are interesting. Then we will play with 4 hits. We drag the ruler, measure the sizes of the elements and try to find the divisors.
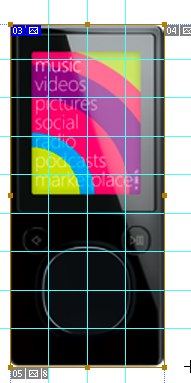
Explains sarcoidosis and aggressive behavior ... hell, it seems I am writing to the wrong window. In general, here again dull squares, which few people confuse. Spoiled such a good start.
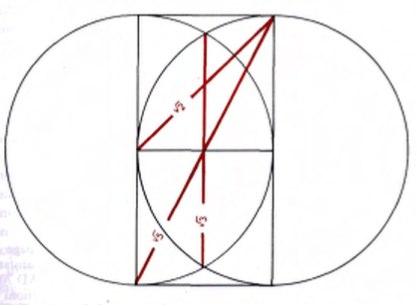
We'll have to go back to the iPods again. iPod Nano 2G also has a √5 / 1 aspect ratio. Let's look at the diagram from the manual again and think about how to stick it to something. Yeah. There is a side √5 that can be squeezed into the previous construction.

From points A, O, and C, we draw arcs with radius AB (since this is 1x and AC is √5x). From the same points we draw perpendiculars to AC to the intersection with arcs. Connect the new intersections and now our iPod is almost ready.

Ahaylai, mahalai, abra cadabra!

So what have we learned?
1. If you want to confuse people’s head, you should always use the mystical numbers √2, √3, √5 and φ. With them there will always be the most “mysterious” coincidences. There are many more interesting things like Fibonacci sequences, spirals, gnomic enlargements and all sorts of tricky divisions. But the simpler - the easier it is to confuse everyone, right?


2. Apple is definitely brainwashing people. After all, they have a whole set of young occultists:

3. From a simple square, you can construct a whole brain explosion, religion, algebra, the dichotomy of good and evil.
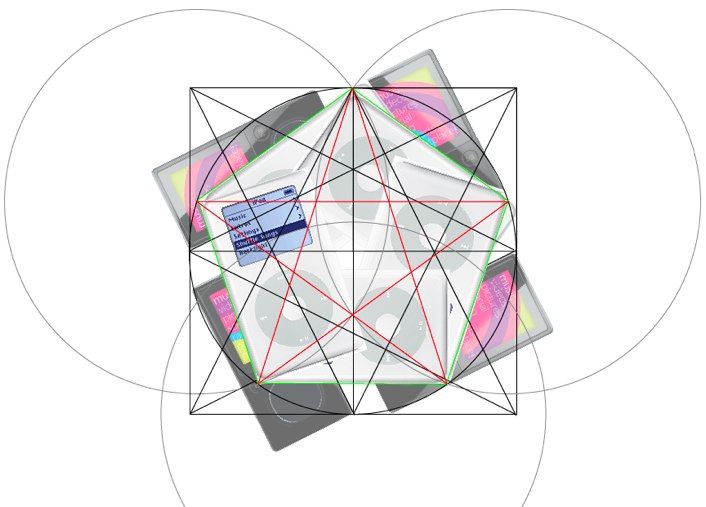
Everyone will see what they want here, including boobs and Mickey Mouse (you can still see the star of David, if you care).
Such is the property of man - to distort simple ideas. But here is where it all began:

In the previous ( 1 , 2 , 3 ) parts, we saw how different proportions were used in geometry, ancient art, and modern industrial design. We still have an unsolved topic of the golden ratio and another root - √5. Let's start.
Once, people came across the idea of proportions. In different figures the same patterns were constantly met. It was impressive. Then someone thought of measuring a couple of plants, animals and some parts of the body that are usually hidden from strangers. Patterns were there. It was even more impressive.
There is no more urine left, the most common relationships have been declared sacred. Some saw in them a manifestation of divine intervention. Some are of God himself. And since sacred proportions are so often found, then you can fit whatever you want under them, make a symbol out of it and frighten the flock.
Hoaxes and postscripts from the best of intentions are found in history constantly. For example, the scribes of the classic work “Church History of the People of the Angles” of the Venerable Bad’s attached pieces to the text so that certain church questions would look more favorable. And 25-28 of chapter VI of the book "Notes on the Gallic War" by Caesar apparently not so Caesar.
The same is true in symbolism. It is necessary that people feel its deepest meaning, and the form itself is not so important. Take any picture, in it surely yes something will be found. The older the better. Our oldest Egypt, exercise on it.
Here is a bas-relief diagram of the tomb of Petosiris, found in 1919.

After sitting enough time with a ruler and compass, you can find in it a golden ratio and a bunch of different relationships (besides text letters, wits, you don't need a compass for this).

It looks pretty cool, so there is no reason not to say that the Egyptians knew about the Golden Ratio and did it on purpose.
Mystifying geometry is easy and simple. Now I will show you a couple of tricks. Look under the cat.
So, the tricks. Well, firstly, all these proportions are so ancient that all the coolest constructions are well described. Having opened the directory, we see how to simulate the very golden proportions in the simplest way. We take a square, draw end-to-end the same and draw the diagonal AC.

With a center O and a radius OA, we draw a circle. Extend the FE line to the point of intersection with the circle K. Then you can repeat the focus with the circle for side AB, but it is easier to draw the perpendicular KH from K, extend AB and mark the intersection point of H.

Voila, we get a “golden rectangle”. The ratio of FE to EK is the same as FK to FE. Even more awesome, KF / FB also equals this. For brevity, the Greeks called this relation φ (Phi). It is approximately equal to 1.618 We
show creativity and make a couple more passes. Connect the corners of the original square and the resulting rectangle. Let's draw a circle on the formed points.

Now, to open the veil of great mystery, we need to find something to fit into this rectangle. Remembering how lucky we were with Apple, let's go the simplest way and make the obvious.

Hurrah! We managed to declare the iPod 4G a sacred device. It is obvious that now they will definitely buy it.
Here it is - the benefit of studying textbooks. Geometry has existed for so long that it costs nothing to take reference books, and classical sources, write books and earn a lot of profit on it.

You look, the book is being filmed with an actor of a form that has gone awry from the script, and the profit will be an order of magnitude more. You can compost the reader’s brain, or you can compost the reader’s brain by how you can compost the reader’s brain - also, by the way, profitable (well, you know what I mean, my well-read commentators). To the extreme, you can hit contemporaries and earn some advantages by solving the secrets of the Arabian mosaic, linking it ... well, let's say with a bee.

In fact, in art, of course, it is all about ordinary modular grids and guide lines that artists and designers use to compose compositions. The idea is so old that even the oldest of the ancient Egyptians used it.

Compositions are taught in art schools, and those who also teach someone once taught. So no mystery. Unless only the very first teacher invented something there. The rest is enough to take some kind of grid and place elements on it.

But the one and a half aspect ratio and square modules are not interesting. There is no secret. It’s better to take something more sacred. Let's say one more known relation is √5. The Zune player is just that.

Let's look at the directory and see what patterns may come up.

We put them on the player. Hm. There is nothing similar yet. Let's try to sort through all the options.

Ummm ... It's somehow rotten. Only touches near the central button are interesting. Then we will play with 4 hits. We drag the ruler, measure the sizes of the elements and try to find the divisors.

Explains sarcoidosis and aggressive behavior ... hell, it seems I am writing to the wrong window. In general, here again dull squares, which few people confuse. Spoiled such a good start.
We'll have to go back to the iPods again. iPod Nano 2G also has a √5 / 1 aspect ratio. Let's look at the diagram from the manual again and think about how to stick it to something. Yeah. There is a side √5 that can be squeezed into the previous construction.

From points A, O, and C, we draw arcs with radius AB (since this is 1x and AC is √5x). From the same points we draw perpendiculars to AC to the intersection with arcs. Connect the new intersections and now our iPod is almost ready.

Ahaylai, mahalai, abra cadabra!

So what have we learned?
1. If you want to confuse people’s head, you should always use the mystical numbers √2, √3, √5 and φ. With them there will always be the most “mysterious” coincidences. There are many more interesting things like Fibonacci sequences, spirals, gnomic enlargements and all sorts of tricky divisions. But the simpler - the easier it is to confuse everyone, right?


2. Apple is definitely brainwashing people. After all, they have a whole set of young occultists:

3. From a simple square, you can construct a whole brain explosion, religion, algebra, the dichotomy of good and evil.

Everyone will see what they want here, including boobs and Mickey Mouse (you can still see the star of David, if you care).
Such is the property of man - to distort simple ideas. But here is where it all began:

