Entangled quantum physics

The phenomenon of quantum entanglement, when particles separated in space interact in a mysterious way with each other, cheekily violating the prohibition on the transmission of interactions with superluminal speed, has long been considered part of science and has no doubt among the scientific community. The prospects for creating quantum computers on this basis are being seriously studied. It is believed that their data elements - qubits will change and transmit their information state through the mechanism of quantum entanglement. A pragmatic organization like DARPA generously funds this wonderful science. Meanwhile, the point of view, according to which quantum entanglement in the sense of the EPR paradox, is a myth that has taken root in the surface layer of understanding quantum mechanics, has a good reason.

EPR Paradox

Einstein launched an attack on quantum mechanics with a banner in his hands, on which was written “God does not play dice”. In the famous article [0], published in 1935, appeared the so-called. EPR paradox (Einstein, Podolsky, Rosen). From this paradox, which is actually a sophism, the myth of quantum entanglement was born.

The main idea of ​​the EPR, according to the article of its authors, is as follows. Let there be a pair of quantum objects 1 and 2, forming a single system with the wave function$$Ψ ( x 1 , x 2 ) , where the sets of variables$$x 1 and$$x 2 are used to describe the behavior of subsystems 1 and 2 separately. If given a complete set$$u 1 ( x 1 ) , u 2 ( x 1 ) , ... , u n ( x 1 ) , ... own wave functions for some observable systems 1, then the function$$Ψ ( x 1 , x 2 ) decomposes into a Fourier series:

$$Ψ ( x 1 , x 2 ) = ∞ Σ n = 1 φ n ( x 2 ) u n ( x 1 )

Now suppose that the subsystems move away from each other and after some time the distance between them became so large that mutual influence is impossible. If we then measure the values ​​of (commuting) observables of system 1, then, by virtue of the principles of quantum mechanics, it will jump abruptly into some proper state$$u k ( x 1 ) . In the context of a confusing paradigm, this event has the dramatic name “wave function collapse”. Consequently, the EPR authors further argue, the entire system as a whole abruptly passes into the state with the wave function$$φ k ( x 2 ) u k ( x 1 ) . This means that subsystem 2 was suddenly able to$$φ k ( x 2 ) , although there was no impact of subsystem 1 and measuring instruments on it.

We have before us the main effect with which the idea of ​​the nonlocality of quantum mechanics is connected, namely, the incomprehensible and inexplicable, instantaneous interaction of remote quantum objects 1 and 2. It is that when measuring some physical quantities associated with system 1, automatically and immediately the state of system 2 changes.

In the above reasoning there are two errors at once. The first is that the wave function$$φ k ( x 2 ) u k ( x 1 ) , generally speaking, does not correspond to the own state of the unified system. Therefore, the latter is not required to go into$$φ k ( x 2 ) u k ( x 1 ) is a jump in measurement associated only with system 1. Yet the question arises: what state will be subsystem 2 after measurement 1? The answer is simple and obvious - her condition will not change. Indeed, since in the situation under consideration objects 1 and 2 are independent, then

$$Ψ ( x 1 , x 2 ) = Ψ 1 ( x 1 ) Ψ 2 ( x 2 ) = Ψ 2 ( x 2 ) ∞ Σ n = 1 c n u n ( x 1 ) = ∞ Σ n = 1 c n u n ( x 1 ) Ψ 2 ( x 2 )

Where $$Ψ j ( x j ) is the wave function of the system$$j = 1 , 2 , considered separately. Therefore, as soon as subsystem 1 is in its own state$$u k ( x 1 ) , subsystem 2 automatically appears in ... its initial state$$Ψ 2 ( x 2 ) . What should be expected!

The second error is that a pair of non-interacting objects 1 and 2, formally combined into a single system, does not actually experience a disturbance in the measurement, which is associated only with subsystem 1. Such a “disturbance” is not capable of causing a jump in the unified system into one of eigenstates (the full set of commuting observables obtained by combining sets 1 and 2). For this, it would be necessary to perturb the entire system as a whole, i.e., to actually act also on the object 2.

Thus, the pseudoparadox EPR only forces us to clarify the concept of perturbation. But instead, it is given an absolute and formal meaning, as if the flap of a butterfly's wing was considered a perturbation of the Universe, ... although from a philosophical point of view it is so. The above is the exact answer to the question of what exactly happens to subsystem 2 after measurement 1. In essence, nothing!

From their pseudoparadox, the EPR authors drew far-reaching conclusions about the incompleteness of quantum mechanics, i.e. that this theory needs additional parameters to describe quantum systems. Parameters that eliminate any uncertainty and make their behavior deterministic in the classical spirit. From the point of view of Einstein, science simply does not yet know these hidden parameters and the laws of their behavior; therefore, it is limited to the probabilistic nature of quantum predictions.

In popular explanations of the quantum entanglement effect of a pair of particles, after a free exposition of EPR, they always refer to the conservation laws. Consider the case of a pair of electrons. There is no point in discussing the conservation of momentum, although an example is often given of a pair of "entangled" electrons with pulses.$$± → p . Since the pulse operator has a continuous spectrum, its own states can hardly be realized. Therefore, at the quantum level, it is meaningless to consider a pair of electrons with pulses$$± → p . Thus, we discard the momentum to the side and consider the case of an “entangled” pair of electrons with zero total spin projection onto the Z axis (singlet).

Preserving the spin projection means that for the operator$$m z projection of the spin on the Z axis takes place$$[ m z , H ] = 0 , where$$H is the energy operator of this system. In particular, this means that if the system is initially in the operator’s own state$$m z , then in the future, in the absence of external disturbances, it will be for each$$t be in one's own observable state$$m z , although the state vector may vary with time.

For a single electron, the operator$$m z has two eigenvectors, we denote them$$| 1 ⟩ and$$2 ⟩ , so

$$m z ( | 1 ⟩ ) = 12 h2 π | 1⟩m z ( | 2 ⟩ ) = - 12 h2 π | 2⟩

Suppose that a pair of electrons is initially in the state $$c ⋅ ( | 1 , 2 ⟩ - | 2 , 1 ⟩ ) , where$$c is any complex number. Here is a vector$$| a , b ⟩ answers such as a pair of the first electron is in a state$$| a ⟩ , and the second in the state$$| b ⟩ . condition$$c ⋅ ( | 1 , 2 ⟩ - | 2 , 1 ⟩ ) it is proper for a spin$$M z systems of two electrons, so when measuring the system will remain in this state and a zero value will be obtained$$M ' z = 0 for a pair of spin.

In the process of scattering electrons in different directions, the spin state of the singlet will not change if the system remains isolated up to the time of the first measurement. This means that with each$$t a pair of electrons is in the state$$c ( t ) ⋅ ( | 1 , 2 ⟩ - | 2 , 1 ⟩ ) , which is a private operator$$M z and corresponds to the eigenvalue$$M ' z = 0 . According to popular reasoning about a pair of entangled electrons, when measuring the spin of one of the particles, the system will jump to its own state$$M z . But according to quantum mechanics, since the system is already in its own state (the full set of commuting observables, including$$M z , it will remain in it after measurement. Accordingly, only the numerical factor in front of the vector will change.$$| 1 , 2 ⟩ - | 2 , 1 ⟩ .

Thus, the transition of the measured electron to the state$$| 1 ⟩ , and in the second state$$| 2 ⟩ not happen. It is a contradiction with the fact that the measured electron still goes into the own state of its operator$$m z . It follows that when measuring the spin of one of the electrons, the joint state of the singlet will be destroyed. In this case, the state of the second electron will remain unchanged, i.e., indefinite from the point of view of the spin, namely$$| 1 ⟩ + | 2 ⟩ .

In the framework of the entangled paradigm, a pair of photons in the same polarization states are also considered, so that the overall state of the pair can be set by the vector$$c ( | 1 , 1 ⟩ + | 2 , 2 ⟩ ) , wherein$$| 1 ⟩ and$$| 2 ⟩ set the polarization state in perpendicular directions. If, when measuring one of the photons, it goes into its own state$$| 1 ⟩ , then supposedly it will cause a transition to a state couples$$| 1 , 1 ⟩ , i.e., instantaneous jump in the second photon in the same polarization state$$| 1 ⟩ . However, similarly to the example with a singlet of electrons, it can be argued that a pair of photons will remain in its own state$$c ( | 1 , 1 ⟩ + | 2 , 2 ⟩ ) . This contradiction means that measuring one of two photons destroys the system, after which the second photon remains in the initial state.$$| 1 ⟩ + | 2 ⟩ . Entanglement in the sense of EPR does not arise here either.

Bell inequalities

In 1964, John Stuart Bell wrote an interesting article [1], in which he subjected to a critical analysis a hypothesis about hidden parameters. These surprisingly simple Bell arguments have had a great influence on the development of quantum physics from the late 20th century to the present.

In the course of his reasoning, Bell derived inequality$$1 + P ( → b , → c ) ≥ | P ( → a , → b ) - P ( → a , → c ) | where$$- these are the unit vectors of different directions in space, onto which the spins of two particles (electrons) running in different directions are projected. Initially, the particles have zero total spin, i.e. form a singlet. Wherein$$ denotes an unregulated correlation coefficient of a pair of random variables $$ and $$that are projections of spin variables $$ and $$ particles 1 and 2 on the directions of vectors $$ and $$respectively. In other words$$ Is the average of the product of numbers $$ and $$. Which, we note, take values$$. This inequality holds under the condition that Einstein's hypothesis about hidden parameters is true.$$quantum system. And it can be verified statistically. Later on, other inequalities were obtained similarly, which are applicable not only to the singlet pair of electrons, and all of them are called Bell inequalities. For example:

$$

It is also valid only if there are hidden options. $$quantum systems defining its behavior. In this case, since the laws of behavior of these parameters are unknown, they are considered random variables.

To illustrate the last statement, consider the experience of throwing a coin. It is clear that the flight of an abandoned coin is determined by many quantities that describe its shape, mass distribution, detailed throwing conditions, the shape of the surface of the fall, and other factors that determine the answer to the question: “heads or tails”. With full consideration of all these “hidden parameters”, which Bell designates with the symbol$$, it would be possible to give a 100% reliable prediction of exactly how the coin will fall. However, such an account is too complicated, and there is no great need for it, so they are content with a probabilistic forecast of how the coin falls. Accordingly, the hidden parameters should be considered random variables. Question: are there any similarly hidden parameters for any quantum system, or are there no such parameters, and the stochastic behavior of subatomic objects is inherent in the nature of things?

In experiments with the so-called. entangled particles, most often photons, the desired result is always a violation of Bell's inequality. Such violations have actually been observed since the late 70s of the last century, and today it is customary to interpret them as evidence of the occurrence of entangled quantum states. At the same time, significant efforts of experimenters are aimed at spreading as far as possible the devices that register the spins of the particles or the direction of polarization of the photons in order to eliminate the mutual influence of objects and measuring devices. Having thereby made the most convincing effect of the instantaneous transmission of interactions, underlying the fantasies of quantum teleportation.

However, in reality, a violation of Bell's inequalities means one of two things.

a) Quantum systems have no hidden parameters. This is fully consistent with quantum mechanics and is not associated with entanglement.

b) The hidden parameters are there and then the measurements of one of the subsystems can affect the other. Therefore, quantum entanglement takes place.

Accordingly, there is no reason to assert that the violation of Bell's inequalities experimentally prove the EPR phenomenon - entanglement. It is reasonable to assume that they entail a), that is, that quantum mechanics does not need hidden parameters and an upgrade in the spirit of Bohm. However, these violations are considered to be evidence of EPR - entanglement of photon pairs.

This paradigm was formed under the influence of the work of Aspe and other scientists who set up similar experiments. In addition to the undoubted violations of Bell's inequalities, they allegedly observed correlations between the polarization directions of mutually distant photons. If this were so, there would be no need for experiential testing of EPR - entanglement in Bell inequalities. It should be noted that Aspe himself, judging by the article [1], considered only correlation evidence of entanglement. But in reality, there was a “correlation” of each photon that entered the photomultiplier with itself. More precisely: he reached two photomultipliers almost simultaneously (see below).

Aspe Experience

The experience of Alan Aspe (Aspect), a brilliant experimenter and classic of quantum magic, made the main contribution to the transformation of EPR, a myth into a dogma. The results of Aspe's and others' experiments were interpreted on the basis of the concept of photons as point particles (with the usual reservations about wave-particle duality). It is erroneous, since the photon has no Schrödinger representation [2]. In simple terms, for these particles, the concept of spatial coordinates is meaningless. Therefore, it cannot be said that at a certain point in time the photon is in a certain place. It can be localized in the state of a small wave packet, but in this case the polarization loses its meaning.

In this regard, it is appropriate to quote Dirac (PAM Dirac, p. 25 [2]).

"...Suppose we have a beam of light, consisting of a large number of photons, which splits into two components of the same intensity. Assuming that the beam intensity is related to the probable number of photons, we would get that half of the total number of photons would fall into each of the components. If further these two components interfere, we must require that a photon from one component can interfere with a photon in another component. Sometimes these two photons would be destroyed, sometimes they would turn into four photons. This would be contrary to the law of conservation of energy. The new theory, which links the wave function with probabilities for one photon, overcomes this difficulty, considering that each photon is partly in each of the two components. Then each photon interferes only with itself."

A similar thought sounds in a quotation from Heisenberg that deals with the EPR paradox and relates to the interpretation of Aspe's experiments (W. Heisenberg, p. 34 [3]).

"In connection with these considerations, the thought experiment proposed by Einstein should be pointed out here. Imagine a single light quantum, which is represented by a wave packet built from Maxwell waves and to which, thus, a known region of space is attributed and, in the sense of uncertainty relations, also a certain frequency region. Through reflection from a translucent plate, we can obviously easily decompose this wave packet into two parts: reflected and transmitted. Then there is a certain probability to find a light quantum either in one or in another part of the wave packet. After a sufficiently long time, both parts will be as far away as possible from each other. If by means of experience it is now established that the light quantum is, say, in the reflected part of the wave packet, then it will simultaneously give that the probability of finding a light quantum in another part is zero. The experience in place of the reflected half of the packet thus produces some action (mixing the wave packet!) At an arbitrary distance from the other half, where the other half is located, and it is easy to see that this action propagates with superluminal velocity“

Thus, attempts to detect EPR are entangled photon pairs using an interferometer are meaningless. Suppose we split the light beam with a semitransparent mirror, and then we passed one beam through a polarizer. According to the EPR paradigm, entangled pairs of equally polarized photons from two beams appear. can be checked through the interference, but since each photon will interfere with itself, the coincidence of the measured polarizations in different places can not be construed as EPR - entanglement.

Implicitly assumption Guy possibility photon polarization point was the basis Aspe false interpretation of the experiments. We begin with a brief description of these experiments (details in [1]).

Used fluorescent sources of cascade radiation, where atoms emit pairs of quanta with an interval $$ns In the first experiments, one of the photons of the pair had a wavelength of 551.3 nm (green light), and the other 422.7 nm (violet). Based on the laws of conservation of momentum and angular momentum, it is considered that in each cascade photons fly apart in different directions, having the same directions of circular polarization - left or right with probabilities of 0.5, which is equivalent to being in a superposition of two linear polarization states in the directions of the X and Y axes. Aspe and his followers believe that this pair of light quanta is born in an entangled, polarized state:

$$

$$

States $$, $$ meet the directions of polarization along the coordinate axes, the state $$, $$ - two directions of circular polarization photon number $$.

EPR - entanglement means that if one of the photons is detected polarized along the X axis (for which it is enough to pass it through a polarizer with X - orientation), then the second will automatically, at the same instant it will be in the same state (which can be detected using the second polarizer). The same is true for the Y axis. In this case, it is said that there is a correlation between the directions of polarization of the photons of the entangled pair, which can be measured.


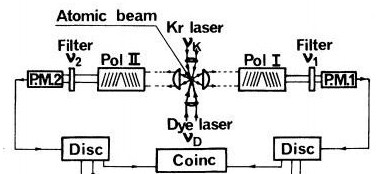
Experiment scheme Aspe

In the diagram, a pair of lasers excites a fluorescent source of cascade radiation, which, according to Aspe, emits pairs of entangled photons. Each of them passes through its own polarizer (Pol I and Pol II), after which, passing through a frequency filter, it enters the photomultiplier (PM I and PM II). The latter is essentially a single photon detector and operates on the principle of an electron avalanche, which is initiated by the photoelectric effect. The control circuit of the photomultipliers is organized so that each pair of quanta is detected in a time window of about 20 ns. A random pair of photons from two different atoms is unlikely to hit it. Thus, the scheme will almost certainly fix only a pair radiated in one cascade. It happens on average 100 times per second. Recall that each such pair is considered to be EPR - confusing.

If now for a certain period of time to count the number of pairs for the cases when one of the polarizers (“left” or “right”) is removed, then you can calculate the correlation coefficient between the polarization events of the left photon in a given direction $$, and right in the direction $$. Such measurements make it possible to check Bell's inequalities, and also reveal a correlation between the polarizations of the photons of each pair (for different directions$$ and $$). That is what was done by the Aspe group.

However, in Aspe’s experiment, there could be a counting of single photons that reached two photomultipliers in the form of waves with spherical fronts (wave surfaces). According to quantum electrodynamics [4], the photon field with a given angular momentum propagates precisely in the form of such a wave. It can be proved that this wave comes to each of the two polarizers in the same phases, although at different points in time due to different distances from the emitter. The angle between the field strength vector$$and the axis of each polarizer is the same for any wave surface. Therefore, a single photon wave interacts with two polarizers in the same way. This creates the illusion of a pair of particles entangled in polarizations.

To this, one can argue that the photon counter operates twice on average through$$ns, as it should be when emitting cascades. However, the response time of the photomultiplier elementary estimated$$ns During this time only one photon can be recorded. In fact, it is a wave packet centered on a sphere.$$. If the package size$$ m, which corresponds to the Doppler broadening of the spectral line $$, the time of passage through the photomultiplier is of the order of the interval between the photons of a single cascade. Under the conditions of Aspe's experiments, such broadening was possible. Thus, until the pair of photomultipliers operates on the first photon, the second one could not be detected, and by the time both devices are ready to receive the second photon, its packet has already passed. Apparently, in most cases, a pair of photomultipliers recorded only one of the two photons of each cascade.

Note also that in the state under consideration the direction of the photon's motion is not determined. This is due to the fact that the impulse and its moment do not commute. Consequently, the analogies with classical mechanics, which are used as the cause of the entangled state of a pair of photons, are inappropriate in this case. In addition, the emission of a photon is accompanied by a disturbance. After it, the atom will not be in a state with zero moment, but in a superposition of the eigenstate states of the moment. Thus, the conservation laws do not entail the state of a pair of photons of a single cascade of the form

$$

During the radiation time the distance between the photons of the pair will be $$m. The idea that such a pair is born confusing, contrary to common sense. However, the latter applies to all quantum magic.

Thus, the results of Aspe's experiments have an interpretation that is not related to EPR - entanglement. More accurate estimates are needed, but there is already reason to assume that in these experiments joint, EPR — entangled states were not observed. Apparently, in this way it is possible to explain all the experiments with the so-called. entangled photons.

The concepts of entangled states of mutually distant particles, going back to the EPR paradox, are widely popularized and are already considered part of quantum mechanics. One of the goals of this article was to show that there is no foundation for this. The bubble in the illustration symbolizes the wave front of a photon with a given angular momentum, as well as the theory of quantum computers based on EPR - entanglement.