Passage sapper. Part 2.
After the publication of the topic , many interesting, useful, and pleasant comments were received. Thanks to this, I continued to study the issue, redid the calculation algorithm and received some interesting facts (including the probability of winning with a different number of mines), which, I think, will interest you.
The advice on exhaustive search made me think, because at first I did not take it seriously, considering that the search would take a very long time. This would indeed be the case if mines were scattered across the entire field. But after downloading the sapper from IXBT , I realized that this was not necessary at all. It makes sense to consider only those cells that are directly adjacent to open numbers. These numbers do not affect the likelihood of mines in other cells.
By the way, having studied the downloaded sapper, I found that it does not at all take into account the remaining number of mines in the field when calculating. At first glance, this is not critical, since, for example, around a single “4” probability there will always be 50/50. But there are cases when the neglect of this factor leads to very bad consequences, for example: The
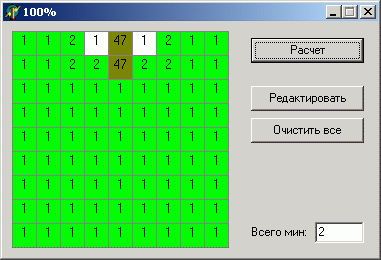
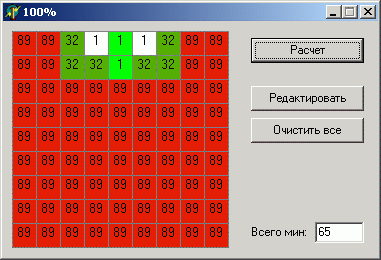
data is exactly the same, except for the number of mines, but the difference in result is very significant.
I think you yourself guess why this is happening. There are 2 ways to arrange mines: one mine between units (there are no more nearby) or two mines, one for each unit. If there are 2 mines on the entire field, then most likely one will be located between units, but the second can be in almost any cell of the field than both will be nearby. Conversely, if there are a lot of mines, then the probability that there will not be a single mine in the area of 6 cells (near the units) is not large.
Now the calculation from IXBT:
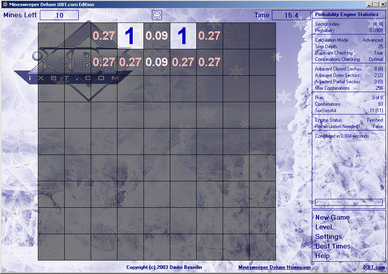
For any number of mines, the probabilities are the same. Based on his data, I came to the conclusion that when enumerating options, he implies that they are all equally probable, but, as can be seen from the example, this is completely wrong.
Calculating the probability of each case added a bit of trouble to me. If in the process of enumeration the variant met the conditions, then it was necessary to calculate the probability of this case, and add the obtained number to all cells with mines (hypothetical mines obtained only for the current version). Although the calculation itself is not difficult, only the basics of combinatorics are used.
It would be nice to end up on this good note, since everything went very well, and the obtained probabilities were fully confirmed by theoretical calculations and the first version of the program. But this is if the number of cells bordering open numbers was not very large. With the number over 23, the calculation took more than a second, which was not very pleasant. Therefore, a proven method was adopted (Monte Carlo, as noted in the previous topic). A random set is generated in the same neighboring cells, which allowed to increase the number of iterations from 10 thousand to a million. Unfortunately, in complex cases, an error is still issued, but this happens much less often. But in general, it works accurately and quickly. You can download it here .
When the program was ready, it became interesting to check the frequency of winnings from the number of mines. Games were held from a thousand to a million, depending on complexity and time. The diagram shows only numbers from 1 to 32, so the probability becomes very small. The rest is below. As you can see, the function is quite smooth. I tried to find an empirical formula for it, but so far to no avail, so it would be great if you tell me. Especially for M_org , who asked me if I could pass with 64 mines, I drove 10 million times and never won. But now I can safely answer that it’s not weak even with the 79th :)

The advice on exhaustive search made me think, because at first I did not take it seriously, considering that the search would take a very long time. This would indeed be the case if mines were scattered across the entire field. But after downloading the sapper from IXBT , I realized that this was not necessary at all. It makes sense to consider only those cells that are directly adjacent to open numbers. These numbers do not affect the likelihood of mines in other cells.
By the way, having studied the downloaded sapper, I found that it does not at all take into account the remaining number of mines in the field when calculating. At first glance, this is not critical, since, for example, around a single “4” probability there will always be 50/50. But there are cases when the neglect of this factor leads to very bad consequences, for example: The


data is exactly the same, except for the number of mines, but the difference in result is very significant.
I think you yourself guess why this is happening. There are 2 ways to arrange mines: one mine between units (there are no more nearby) or two mines, one for each unit. If there are 2 mines on the entire field, then most likely one will be located between units, but the second can be in almost any cell of the field than both will be nearby. Conversely, if there are a lot of mines, then the probability that there will not be a single mine in the area of 6 cells (near the units) is not large.
Now the calculation from IXBT:

For any number of mines, the probabilities are the same. Based on his data, I came to the conclusion that when enumerating options, he implies that they are all equally probable, but, as can be seen from the example, this is completely wrong.
Calculating the probability of each case added a bit of trouble to me. If in the process of enumeration the variant met the conditions, then it was necessary to calculate the probability of this case, and add the obtained number to all cells with mines (hypothetical mines obtained only for the current version). Although the calculation itself is not difficult, only the basics of combinatorics are used.
It would be nice to end up on this good note, since everything went very well, and the obtained probabilities were fully confirmed by theoretical calculations and the first version of the program. But this is if the number of cells bordering open numbers was not very large. With the number over 23, the calculation took more than a second, which was not very pleasant. Therefore, a proven method was adopted (Monte Carlo, as noted in the previous topic). A random set is generated in the same neighboring cells, which allowed to increase the number of iterations from 10 thousand to a million. Unfortunately, in complex cases, an error is still issued, but this happens much less often. But in general, it works accurately and quickly. You can download it here .
The main objective.
When the program was ready, it became interesting to check the frequency of winnings from the number of mines. Games were held from a thousand to a million, depending on complexity and time. The diagram shows only numbers from 1 to 32, so the probability becomes very small. The rest is below. As you can see, the function is quite smooth. I tried to find an empirical formula for it, but so far to no avail, so it would be great if you tell me. Especially for M_org , who asked me if I could pass with 64 mines, I drove 10 million times and never won. But now I can safely answer that it’s not weak even with the 79th :)

35: 17 (из 10 тыс) 0.17%
40: 10 (из 100 тыс) 0.01%
45: 3 (из 100 тыс) 0.003%
50: 6 (из млн) 0.0006%
60: 2 (из млн) 0.0002%
70: 0 (из млн) ?
75: 6 (из млн) 0.0006%
76: 32 (из млн) 0.0032%
77: 183 (из млн) 0.0183%
78: 1552 (из млн) 0.1552%
79: 25350 (из млн) 2.535%
