Enter the form: from hyperbolic geometry to cubic complexes and back

The proof marks the end of an era in the study of three-dimensional forms.

Thirty years ago, mathematician William Thurston [William Thurston] spoke about his vision: systematization of all possible finite three-dimensional forms.

Thurston, the Fields award winner, who spent most of his career at Princeton and Cornell universities, had a supernatural ability to represent the unimaginable: not only forms that live in ordinary three-dimensional space, but also a much larger menagerie of forms with such complex properties that they can only fit in space with a lot of dimensions. Where other mathematicians saw the beginnings of forms, Thurston saw structures: symmetries, surfaces, the relationship between different figures.


William Thurston at Berkeley in 1991.

“After many years of study, many people have the impression that mathematics is a strict and formal subject dealing with complex and incomprehensible rules,” he wrote in 2009. - Good math is the exact opposite. Mathematics is the art of human understanding ... Mathematics sings when we feel it with the whole brain. ”

At the heart of Thurston’s vision was a marriage alliance between two seemingly incompatible approaches to the study of three-dimensional figures: geometry, the familiar realm of angles, lengths, regions and volumes, and topology that studies form properties that do not depend on exact geometric dimensions — properties not changing, if the form is stretched or twisted, as " handgam ".

For a topologist, the surface of a griddle is equivalent to the surface of a table, pencil or ball; the surface of the mug is equivalent to a donut or torus. From the point of view of the topologist, the variety of two-dimensional forms - surfaces - comes down to a simple list of categories: spherical, toroidal, and toroid-like with a large number of holes. (Most of us are spheres and tori as three-dimensional, but since mathematicians think of them as hollow surfaces, they consider these surfaces to be two-dimensional objects, measured by surface area, not volume).

Thurston's key idea was to understand 3-varietiespossible by combining geometry and topology. Just as the topological category of 2-manifolds, containing the surfaces of a griddle and a pencil, also contains an ideal sphere, Thurston suggested that many categories of 3-manifolds contain one instance, a 3-manifold, whose geometry is so uniform and perfect, so beautiful, that, according to Walter Neumann of Columbia University, it “rings like a bell”. Moreover, Thurston suggested that forms that do not have such an instance can be cut into pieces, which he already has.

In the work of 1982, Thurston put forward his “geometrization hypothesis” among 23 questions about 3-manifolds, which offered mathematicians the direction of knowing three-dimensional forms. (There were 24 questions in the list, but one of them, still not resolved, looks more like an intriguing lane than the main road).

“Thurston had a tremendous talent for asking the right questions,” said Vladimir Markovich, a mathematician from Caltech. “Anyone can ask questions, but it rarely happens that a question leads to insights and beauty in the way Thurston’s questions did.”

The questions inspired a new generation of mathematicians, dozens of whom decided to conduct their work under the leadership of Thurston. His mathematical "kids" express his style, as Richard Brown wrote.from the University. John hopkins "They look at mathematics like children at the fair: with joy and surprise, captivated by each new discovery, and they are just happy to be part of it all."

For decades after the appearance of the work of Thurston, mathematics followed his “map” of research, and their motivation was fed not so much by the possible applications of their discoveries as by the successful place that 3-varieties occupied in the study of forms. Two-dimensional forms are quite banal, they are easy to portray and divide into categories. Four-, five-, and more multidimensional forms are practically practically impossible to train: the variety of possibilities is so great that mathematicians limited themselves to knowing only their special subclasses. And in the case of three-dimensional forms of structure, on the one hand, mysterious and difficult, but on the other - fundamentally knowable.

Thorston’s work has passed 30 years already, and all but four questions have already been resolved, including the geometrization hypothesis, proved by the Russian mathematician Gregory Perelman in 2002, which has become a landmark achievement of modern mathematics. But the four remaining tasks stubbornly resisted.

“The fact that we have not been able to solve them for so long means that something very deep is hidden there,” said Yair Minsky from Yale University.

Finally, in March 2012, Ian Eigol of the University of California at Berkeley alarmed the mathematical community, announcing the proof of the “ Wise hypothesis ”, which closed the last four Thurston questions in one fell swoop.

Mathematicians call this result the end of an era.

“The vision of the 3-manifolds, described by Thurston in his work, could look fantastic at that time, and now it is fully realized,” says Danny Calegari [Danny Calegari] from Caltech. “His ideas were surprisingly proven - and every detail turned out to be correct.”

“It seemed to me that there was a special knowledge and special methods of thinking peculiar to me alone,” wrote Thurston, receiving Steele’s mathematical prize just a few months before his death in August 2012 at 65 years old . “And I am very glad that I have reached such a level when it is not so - many people shared my way of thinking, and many proved theorems for which I unsuccessfully undertook.”

The achievement of Eigol shows the existence of a simple scheme for constructing all compact hyperbolic 3-manifolds - the only type of three-dimensional forms that has not yet been fully explained.

“We now understand exactly what all 3-varieties look like,” says Henry Wilton from University College London. “This is the culmination of a huge mathematical success story.”

Surface study

The Thurston program tried to do with 3-manifolds something that mathematicians successfully did a hundred years ago with two-dimensional manifolds. In order to warm up before understanding three-dimensional manifolds, let's take a look inside the classification of “compact orientable” surfaces (finite surfaces without punctures and cuts with a constant orientation).

To approach the classification problem, mathematicians showed that for any surface it is possible to carry out its sequential simplification, cutting it along curves, until it opens up into a flat polygon.


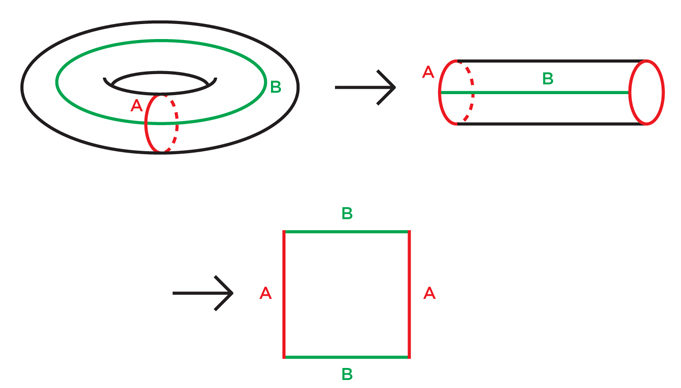
Fig. one

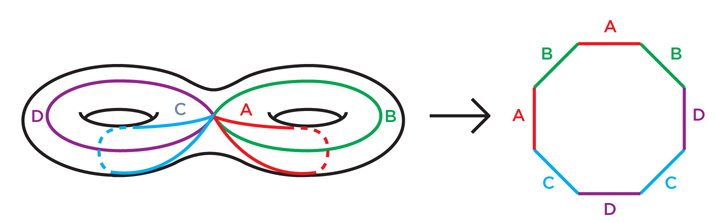
It is easy to show this for a torus: first, we cut it along loop A, as in Fig. 1, we get a cylinder. Then we cut along the loop B, straighten the cylinder into a square. It is a little harder to figure out Figure 2, but even there cutting by four curves turns a double torus (a two-hole torus) into an octagon. In the same way, for any torus with n holes, we can make cuts through the loops of 2n and straighten it into a 4n-gon.


Pic2

You can try to simplify an arbitrary indefinite surface (and identify it) by cutting it in a similar way. If this is not a sphere, topologists have shown that it must contain internal loops (loops that do not intersect each other) that cannot be pulled together into a single point, such as A and B on the torus. Cutting the surface along one of these loops removes several interesting topological properties of the surface. Mathematicians have shown that to reduce a surface to a flat polygon, it is necessary to cut it a finite number of times.

Having simplified the surface to the level of a polygon, it is easy to see that if we glue its edges together, in order to restore the original surface, we will have to make a torus, or a double torus, or a triple torus, etc. After all, the first gluing will turn the polygon into the surface of the tunnel type, and each subsequent one will either add a new tunnel, or simply sew open parts. When we finish the process, we get a torus with some holes.

Such an approach does not simply demonstrate the topological equivalence of a surface to a sphere or some kind of torus: it also provides a way to endow a surface with a simple and uniform geometric structure.

The sphere, obviously, already has a unified geometric structure: its geometry looks the same from any place on the sphere. The surface of the donut, on the contrary, is not at all uniform: the area of ​​the outer edge of the donut is bent in a manner similar to a sphere, and the area on the inner ring is bent like a saddle.

And no matter how you place the torus in space - no matter how you stretch it and twist it - you cannot make it so that in any of its places the geometry is the same. Some parts will round out like a sphere, some like a saddle, some may be flat.

It is possible, however, to provide a torus with an abstract geometric structure that is identical at any point — simply declare that in each of the small sections of the torus, distances and angles are determined by measuring the square from which, as we have seen, you can make a torus. A physical torus in ordinary space, the length and angles of which correspond to this abstract rule, cannot be constructed, but this definition of lengths and angles is internally inconsistent. Since the square has a usual flat (Euclidean) geometry, we say that a torus can be equipped with a Euclidean structure. A torus with such a geometry resembles a video game, in which the character, disappearing from the left side of the screen, reappears on the right, and disappears from the top, appears on the lower.

Trying to do this operation with a double torus, we will encounter an obstacle. Remember that we can make a double torus by gluing together the edges of the octagon. If we declare that the geometry of a double torus should copy the geometry of an octagon, we will face the problem of its angles. After gluing an octagon into a double torus, the corner points will be glued together, into one point of the double torus. At this point, there will be eight corners, each will add 135 degrees, which together will be 1080 degrees instead of 360.

If we try to give the double torus the geometric structure of the octagon, it turns out that our double torus will have the usual Euclidean geometry everywhere except at one point, where its surface bulges out like a pointed hat (corner points are not a problem if we glue a square into a torus: we glue four right angles and we get an ideal 360 degrees).

To get a smooth geometric structure at the corner point of a double torus, each of the eight corners needs to bring in only 45 degrees instead of 135. Interestingly, such an octagon exists, but lives not in an ordinary Euclidean plane, but in another structure called a hyperbolic disk: the third a type of geometry that is uniform and internally consistent, as spherical or Euclidean. But since it is harder to imagine, it was discovered by mathematicians only at the beginning of the 19th century.


Pic.3

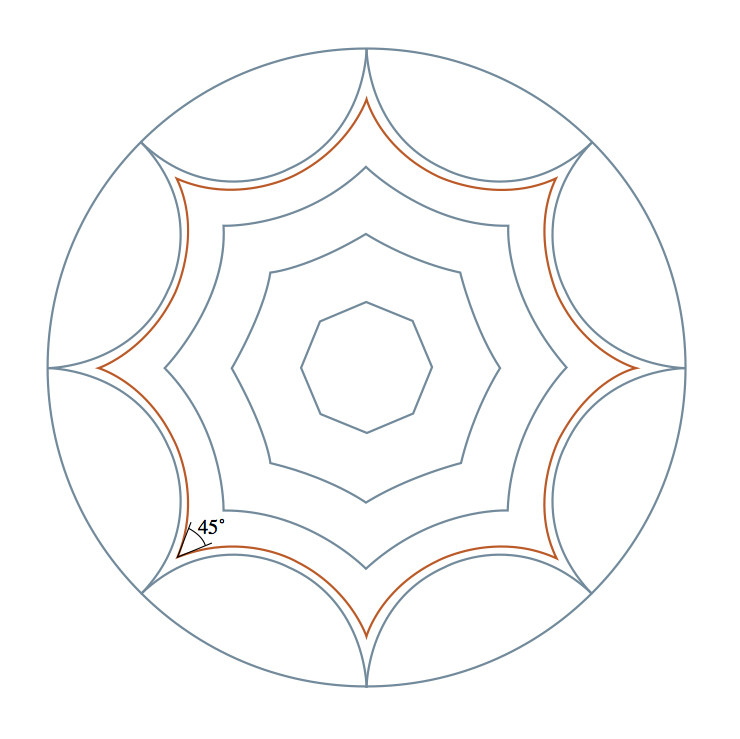
Roughly speaking, the hyperbolic geometry (or Lobachevsky geometry) is obtained by declaring that all the fish in Figure 3 are the same size. One can imagine that Fig. 3 is actually a disk image obtained through a distorting lens, which makes fish closer to the edge smaller than fish in the middle. On a real hyperbolic disk in front of the lens, all fish are the same size.

In ordinary space, it is impossible to make a regular and smooth hyperbolic disk so that all the fish are truly the same. But from an abstract point of view, the rule of fish size gives a geometry that is internally consistent and looks the same at any point — not for an observer with a distorting lens, but from the point of view of a resident of a hyperbolic disk.

In hyperbolic geometry, the shortest path, or “geodesic”, between two points is the path that passes through the minimum possible number of fish. Such a path is always a semicircle perpendicular to the boundary of the disk. Examples are semicircles running along the spine of fish. From our distorted point of view, these paths are curved, but for the resident of the disk these are straight lines. In the words of Thurston, to drive through it, you do not need to turn the steering wheel. In contrast to the Euclidean plane, on which parallel lines always remain at the same distance, two non-intersecting lines on a hyperbolic disk can diverge very quickly from each other.

From the point of view of hyperbolic geometry, the figures in Fig. 4 are regular octagons with straight sides. In one of these octagons, all angles of 45 degrees are exactly what we need for a double torus. If we glue the sides of this octagon correctly, we obtain a double torus with an ideal and uniform hyperbolic structure.


Pic.4

In the same way, we can equip the triple torus with a hyperbolic structure. A triple torus can be glued together from a 12-gon, so if we make a hyperbolic 12-gon with interior angles of 30 degrees, its hyperbolic geometry can be smoothly transferred to a triple torus. Continuing the theme, we can equip a 4-hole torus, with a 5th and so on, hyperbolic geometry. Our classification of compact surfaces is obtained as follows: one surface with spherical geometry (sphere), one with Euclidean (torus), and infinitely many surfaces with hyperbolic geometry (all tori with more than one hole).

Over the past hundred years, this classification has given mathematicians a very fruitful method of transferring topological questions about surfaces into a geometric region, and vice versa. The classification of surfaces is the basic idea in studying two-dimensional forms, a discovery used by all other studies as a starting point.

Next dimension

3-varieties are much more diverse than 2-varieties, and problems with them are more complicated. Even a seemingly simple question, like the famous Poincaré conjecture - which asks whether the three-dimensional version of the sphere is the only compact three-dimensional form on which each loop can be pulled together at one point without catching on the hole - remained unsolved for almost a hundred years after it was set by Henri Poincare in 1904 year

But Turston boldly suggested that it is possible to create a classification of three-dimensional forms similar to the existing two-dimensional classification.

Two-dimensional Euclidean, spherical and hyperbolic geometries have pairs in three dimensions. But in three dimensions, the list of "beautiful" geometries is not limited to them. There are hybrid geometries that are hyperbolic or spherical in certain directions and Euclidean in others. In general, there are eight different types of geometries in three dimensions, uniform in the sense that the geometry looks the same at any point in space.

Thurston suggested that, as with surfaces, 3-manifolds can be compared with natural geometric structures. Specifically, he suggested that if you cut any compact 3-manifold into pieces in a special way, each piece can be compared with one of eight geometries.

“The goal was to completely unify the topology and geometry in three dimensions,” says Minsky.

A natural approach to this “geometrization hypothesis” was to test something similar to what we did with the surfaces that we cut along curves, until they had all the interesting topological properties uncovered, and until they were simplified to a flat polygon. For 3-varieties, a similar approach would be to cut them along surfaces, until, hopefully, they are not simplified to a polyhedron, the opposite sides of which can be glued together to obtain the original shape. And if we can construct this polyhedron using the correct geometry, we can convert this geometry to its original form, as it did with surfaces.

Remember that in the case of surfaces, each curve had to satisfy two requirements: the curve does not intersect with itself (mathematicians say that it must be “embedded”), and it must be, as we call it, topologically interesting, that is, surround some topological detail of the surface so that it cannot be tightened to a point (this requirement ensures that cutting along this curve simplifies the topology of the surface).

In 1962, mathematician Wolfgang Haken proved that a 3-manifold can be simplified to a polygon if the 3-manifold contains a surface whose cut satisfies two conditions: it must be embedded and “incompressible”, that is, any topologically interesting the curve on the surface will also be topologically interesting in the more general context of the surrounding 3-manifold.

For example, a torus will not be incompressible in the usual three-dimensional space, since the loop passing through the hole of the torus is topologically interesting from the point of view of the surface of the torus, but in three-dimensional space it can be compressed to one point. Conversely, the torus is incompressible inside a 3-manifold, which can be obtained by thickening the surface of the torus so that it ceases to be infinitely thin. In order to be incompressible, each topological feature of the surface must reflect some internal topology of the 3-manifold. Now a 3-manifold that has a built-in incompressible surface is called a Haken manifold.

If our 3-manifold has a built-in incompressible surface, then cutting along it will reveal some interesting topologies, and give us a simplified manifold. Moreover, Haken showed that if a variety contains one such surface, then a new variety obtained by cutting along it will also be a Haken variety: it will also have a built-in incompressible surface for cutting. And after a finite number of such steps, as Haken showed, all the interesting topological features of the original manifold will be cut off, and a simple polyhedron will remain.

In the late 1970s, Thurston showed that it is possible to equip the resulting polyhedron with one of eight three-dimensional geometries in such a way that it smoothly transfers to the newly glued polygon, ideally joining at the corners and edges of the polyhedron. In other words, Thurston proved his geometrization hypothesis for those varieties whose standard decomposition results in pieces that are Haken varieties.

Unfortunately, for an arbitrary compact 3-manifold there is no guarantee that it has such a surface. In the late 1970s - early 1980s, Thurston convinced the community that 3-manifolds containing a built-in incompressible surface (Hacken manifolds) are exceptions, not rules.

The search for proof of the geometrization hypothesis for varieties other than Haken varieties has stalled mathematicians for more than twenty years. Finally, in 2002, Perelman presented his proof, based on areas of mathematics far removed from those that were studied by most of the followers of Thurston. (Looking at Perelman’s evidence, he was also stung by Poincare’s centennial hypothesis, which led Clay’s Mathematical Institute to offer him a million dollar prize in 2010 - which he immediately rejected for complex reasons).

The proof of Perelman was a turning point, uniting, as Thurston dreamed, topology and geometry. Now every topological problem associated with 3-manifolds has a geometric pair, and vice versa. But Perelman's theorem left unresolved many important questions about what types of 3-manifolds can exist.

By classifying compact 2-manifolds (surfaces), mathematicians could not only show that each surface can be equipped with a geometric structure, but also make a complete list of all possible 2-manifolds. In three dimensions, such a list was greatly lacking.

Seven of the eight three-dimensional geometries — all except the hyperbolic — were fairly well known, and even before Perelman's work, topologists made a complete description of the types of manifolds that allow one of these seven geometries. These forms are relatively simple and few.

But, as in the case of surfaces, in three dimensions it turned out that most varieties are hyperbolic. And the coverage of a huge number of possibilities of hyperbolic 3-varieties among mathematicians was much worse than for the other seven geometries.

“Of the eight types of geometries, hyperbolic manifolds are the most mysterious and rich,” said Nicolas Bergeron of the University of Pierre and Marie Curie in Paris.

Perelman's result told mathematicians that hyperbolic manifolds were the last frontier — the only type of 3-manifolds that remained to be understood. But he did not tell them what these hyperbolic forms look like.

Cover story

And again, mathematicians were able to turn to the work of Thurston for instructions. In his famous list of questions there were many hypotheses about the properties of hyperbolic 3-manifolds, which included two hypotheses that directly related to their appearance: the “Hacken virtual hypothesis” and the “virtual separation” hypothesis.

Haken’s virtual hypothesis (HGH) asserts that every compact hyperbolic 3-variety is almost a Haken variety in a certain sense: it is possible to transform a variety into a Haken variety by expanding it a finite number of times in a certain way. This new unfolded manifold is called the “final cover” of the original manifold.

Mathematicians say that one variety N covers another variety M, if, roughly speaking, it is possible to wrap N around M a certain number of times (possibly infinite) so that each part of M is covered as many times as all the others. To be a covering, this wrapping should have a bunch of other properties — for example, N should not bend over on itself, or break during wrapping. Each piece of M is covered with a bunch of identical copies in N. covering it.


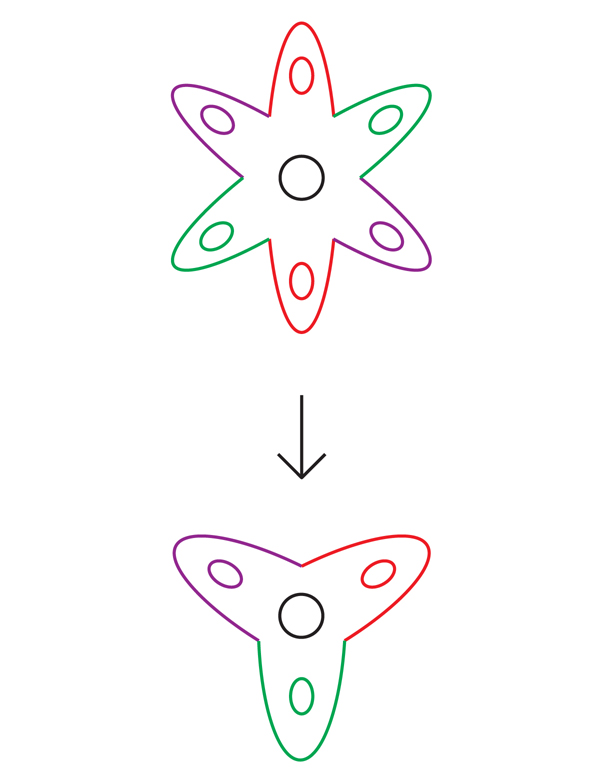
Fig.5

For example, a six-petal flower in Figure 5 covers a three-petal flower: just wrap a six-petal flower two times around a three-petal. Each point of a three-petal color is covered with two six-petal points. Mathematicians call this a two-layer coating.

Similarly, an endless cylinder covers a torus: just wind the cylinder around the torus an infinite number of times (Figure 6). Each point of the cylinder is covered: loop A is covered with an infinite set of loops uniformly distributed over the cylinder, and loop B unfolds on the cylinder in a line running along.


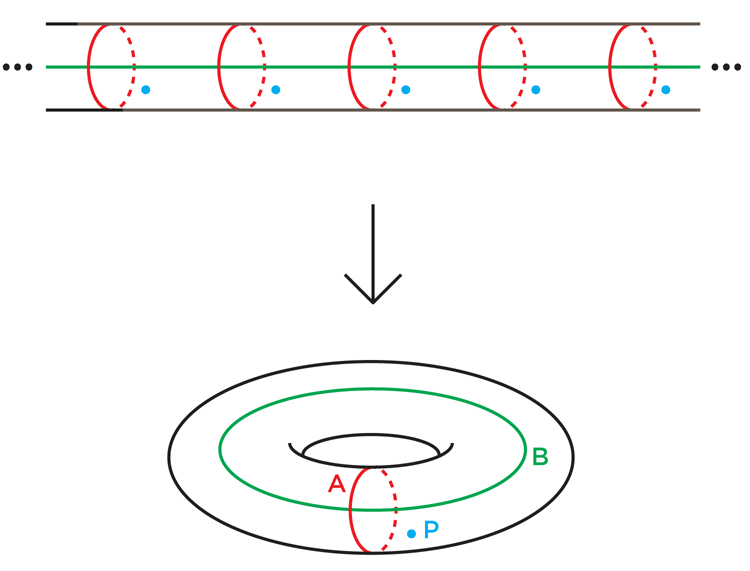
Fig. 6 The

topologies of the manifold and its cover are closely related. To recreate a manifold from an n-layer cover, you just need to fold the cover with itself n times. Conversely, in order to recreate a coating based on a manifold, you cut it, make n copies, and glue it together along boundaries (the concrete coverage you get depends on the choice of the gluing sequence).

The coating retains some topological properties of the manifold, and reveals others. An endless cylinder, for example, remembers that loop A on a torus is closed, but it forgets that loop B is also closed.

This deployment process led Thurston to the hope that for a 3-manifold it is possible to produce a coating with a finite number of layers, which will be a Haken variety. We have already indicated that we should not expect that an arbitrary compact hyperbolic 3-manifold will be a Haken manifold (that it will have a built-in incompressible surface). But in 1968, the German mathematician Friedhelm Waldhausen suggested that such a variety should at least contain an incompressible surface, although it may pass through itself and not be embedded.

If this is true, Thurston argued, there may be a finite covering in which the surface unfolds in a way that eliminates all self-intersections. Final coatings are often simplified in this way. For example, since the curve in a three-petal flower in Figure 7 bypasses around the central hole twice, no stretching and shearing can make it not intersect with itself. But if we turn this curve on a six-petal flower, starting from a certain point P, the resulting red curve (which mathematicians call the “rise” of the original curve) will go around the central hole only once and will not intersect with it. (There is a second ascent, a blue curve intersecting the red at two points, covering the intersection point in a three-petal flower).


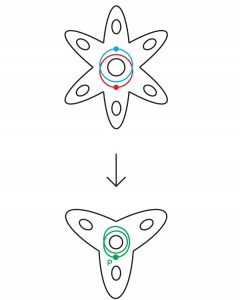
Pic.7

In a 1982 paper, Thurston suggested that if we have a compact hyperbolic 3-manifold, there must be a way to expand it so that we get embedded surfaces in the final covering — that is, the 3-manifold must be “virtually Hacken”.

As we have already seen, the Haken variety can be constructed by gluing together the boundaries of the faces of a polyhedron in a certain way. BGH implies that any compact hyperbolic 3-manifold can be constructed by first gluing the polyhedron correctly, and then wrapping the resulting shape around itself a finite number of times.

Thurston made an even more rigorous assumption: that every compact hyperbolic 3-manifold can virtually stratify, that is, have a finite stratified covering. A variety that “stratifies over a circle” (as mathematicians say) is built by slightly thickening the surface, which makes it three-dimensional, and gluing the inner and outer border together in any way that ensures a smooth connection of the surfaces at each point. (Such gluing is impossible in ordinary space without intersecting parts of the resulting manifold with each other, but it can be studied abstractly anyway). They say about a bundle of a manifold, because one can imagine how the thickened surface is stretched so that the boundary surfaces diverge far from each other, and then unfold and attract them towards each other before gluing, and the resulting manifold resembles a bracelet with an infinitely thin bead shaped like a surface at each point of the bracelet thread. These beads are layers.

Each stratified variety is a Haken variety, but not vice versa. Therefore, the virtual bundle hypothesis is stronger than the AHC, and Thurston was not sure that it is true. "This dubious question, apparently, has a definite chance to get a positive answer," is all that he could have written in his 1982 paper.

Initially, Thurston expressed the CG in an early attempt to approach his geometrization hypothesis, which he had already proved for Hacken 3-varieties. If the BHH was correct, and each compact 3-manifold was Haken's final covering, then perhaps (Thurston hoped), it would be possible to use the geometric structure of the covering to construct the geometric structure of the original manifold.

30 years later, much later than Perelman had proved the geometrization hypothesis by completely different methods, the CG and the virtual stratification hypothesis remained unproved. They, along with two other hypotheses related to them, were the only unanswered questions out of 23. Computer calculations spoke in favor of the truthfulness of the CG - Haken's finite coverings were found for each of the 10,000 hyperbolic 3-manifolds enumerated by the computer. This work was done by Thurston and Nathan Dunfield from the University of Illinois at Urbana-Champaign. But computer busting is not proof.

“When Thurston put forward this virtual hypothesis of Hacken, this question seemed easy. But he stubbornly resisted the decision, which shed light on how little we understand in this area, Minski said. “It turned out that our ignorance in this direction was deep.”

Build surfaces

In 2009, the turbid waters surrounding the VGH began to be purified. That year, Markovic and Jeremy Kahn, then working at Stony Brooke University, announced the proof of a key step to proving the GVD. The result, which we call the “theorem on incompressible surfaces,” postulates that every compact hyperbolic 3-manifold contains an incompressible surface (which may intersect with itself and is not built-in).

The proof of Kahn and Markovic is one of the central examples of the interaction of three-dimensional topology and geometry: the theorem on incompressible surfaces is a purely topological statement, but Kahn and Markovic actively used another structure taken from hyperbolic geometry to prove it.

For the construction of a surface inside a 3-manifold, Kan and Markovich used the property of hyperbolic forms called “exponential mixing”. This means that if you start a path somewhere in a small area within the manifold, choose a direction, and imagine that your region begins to move along a river that flows approximately in a chosen direction, then your region will gradually spread and turn around a 3-manifold, get to any possible place from any possible direction. Moreover, it will do it very quickly in the exact "exponential" sense.

The blending property is unique to hyperbolic 3-manifolds and grows, roughly speaking, from the fact that, in contrast to Euclidean spaces, in hyperbolic space “straight lines” or geodesics are bent relative to each other. If you select a small area of ​​a hyperbolic disk and allow it to move in the chosen direction, it will grow exponentially quickly. Inside a compact 3-manifold, the growing region also grows exponentially, but since the size of the manifold is finite, this region will eventually wrap around it again and again, overlapping itself many times. Moreover - and it is already more difficult to prove - the region will turn around the manifold evenly, passing through all points with approximately the same frequency.

Mathematicians have dealt with this property of exponential mixing more than 25 years ago and have carefully studied the statistics of this “geodesic flow”, approximately having found out when and how often a given area will pass through a certain point. But as long as Markovitch did not take up the incompressible surface theorem, mathematicians could not use this property to construct topological structures in a variety (Another mathematician, Lewis Bowen from the University of Texas A & M tried using exponential mixing for constructing incompressible surfaces in 3-manifolds, but his work came across technical obstacles).

To see how the exponential mixing property helps to build topological and geometric structures, apply it to a simpler task than building surfaces: building a closed geodesic loop whose length is close to our favorite large number (denoted by R).

To build a loop, choose any starting point in the manifold and any starting direction, and then turn on an imaginary irrigation hose located in a small area that includes the starting point, and direct it roughly in the chosen direction. Water droplets will fly along the geodesic path, and while R is large enough, mixing the flow will mean that by the time the droplets have traveled the distance R, they will be distributed approximately evenly across the whole diversity. In particular, at least one drop should return to the starting point area. Then we simply build a small bridge connecting the geodesic of this drop with the starting point to get a loop, almost ideally geodesic, with a length approximately equal to R. It is easy to show that tightening this loop is tighter on the manifold,

Note that the method does not give us a single geodesic loop close to R. In this process, you can use any starting point and any direction, so you can do a lot of such loops. This is the basic principle of constructing structures using exponential mixing.

The exponential blending “asserts that whatever structures in the variety you find, you will find enough of them,” Kalegari says.


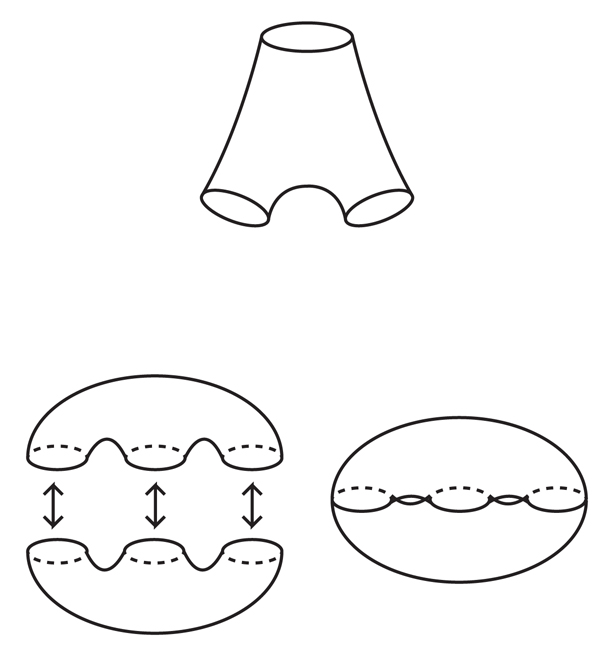
Fig.8

Kan and Markovic used a similar approach to our exercise to create “pants pairs” - surfaces that are topologically equivalent to a three-hole sphere (one for the belt and two for the legs, so to speak). These pants are the starting material for building all compact surfaces, except for a sphere and a torus — for example, gluing (or stitching) two pants gives us a double torus (Fig. 8).

Kan and Markovich showed that for any sufficiently large number of R it is possible to build many pairs of such pants inside the manifold, that their three “cuffs” will be close in length to R and will be almost completely geodesic, that is, each piece of the surface of the trousers will look almost the same from the point view of hyperbolic geometry.

They also showed that for any cuff, the trousers have another pair of trousers, coming from the cuff approximately in the opposite direction. Sewing together these pants at the cuffs, Kan and Markovic received a large family of compact surfaces, almost completely geodesic, with slight wrinkles at the seams. Almost geodesic surfaces are incompressible inside their 3-manifolds; therefore, the construction of Kahn and Markovich proved the theorem of incompressible surfaces.

Also, this method showed that the 3-manifold has not only one incompressible surface, but “the rich structure of almost geodesic surfaces in different places,” Kalegari says.

The work of Kahn and Markovich brought them the 2012 Clay Award of the Mathematics Institute, which was awarded for mathematical breakthroughs.

“Techniques of Kahn and Markovic are not inferior in interest to their results, and this work will undoubtedly inspire many other related research areas,” predicted Jeffrey Brock of Brown University in a 2011 article.

Hidden structure

Kan and Markovic created the starting point for mathematicians who are trying to prove the CG.

They showed that each variety is guaranteed to contain an incompressible surface. But this surface can pass through itself, perhaps in many places, and not be embedded. So that, on the basis of the work of Kahn and Markovic, to obtain the ECU, mathematicians needed to find the final covering of the manifold, in which, exactly as in the example with six- and three-petal flowers, the surface rises to a set of non-intersecting surfaces (although they may cross each other). If this were possible, each of them would be a built-in incompressible surface in the coating, and this means that the coating would be Haken.

But how to find such coverage?

“There is a very big gap between the work of Kahn and Markovic and the VGH,” says Danfield. “Their discovery was important, but it was not clear whether it would help in the search for embedded surfaces.”

The work of Kahn and Markovich attracted the attention of Daniel Wise from McGill University. Wise made a career in research on the removal of self-intersections of topological objects using finite coverages, but he worked in the context of “cubic complexes”, objects that at first glance are very different from 3-manifolds. The work of Kahn and Markovich helped Wise to show other mathematicians that these two contexts are not so different.

The cubic complex - it is the cubic complex (CC): this is a set of cubes, not only a three-dimensional cube is called a “cube”, but also a form in any number of dimensions, consisting of all points whose coordinates lie, say, on the segments between - 1 and +1. For example, a square is a two-dimensional cube, and a segment is one-dimensional. Cubes in QC are connected to each other along corners, edges, faces, and sides of higher dimensions.


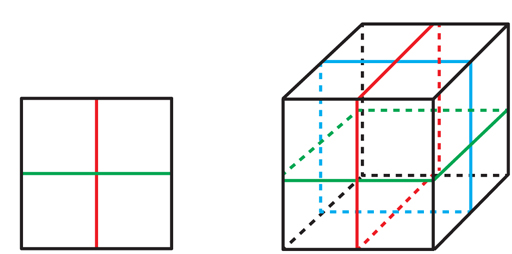
Figure 9

QC is very different from 3-manifolds - they are not even manifolds, since the intersections of two cubes of different dimensions do not resemble the usual space of any of the dimensions. But QA are simplified objects in which one key aspect of a surface contained in 3-manifolds is studied: the fact that such a surface at least locally divides its environment into two parts.

If you need to explore the objects that divide the form into two parts, the cubes are a natural starting field, because of all the possible forms they have the simplest of these objects: the hyperplanes that cut them in the middle. The square has two hyperplanes (GP) - vertical and horizontal lines, cutting it in half. The cube has three GPs (see Fig.9). The n-dimensional cube n GP, ​​intersecting in its center.

“Hyperplanes are akin to surfaces in 3-manifolds, but you see them instantly,” says Wise. “Searching for surfaces is hard, but hyperplanes are available to you right from the start.”

If we start with a GP inside a cube in QA, then there is exactly one way to extend the GP to a GP in neighboring cubes; after that there is exactly one way to expand them to the neighboring ones; and so on. Therefore, for each initial GP in QC there is a unique way of expanding it to GP in the whole QC (see Fig.10).


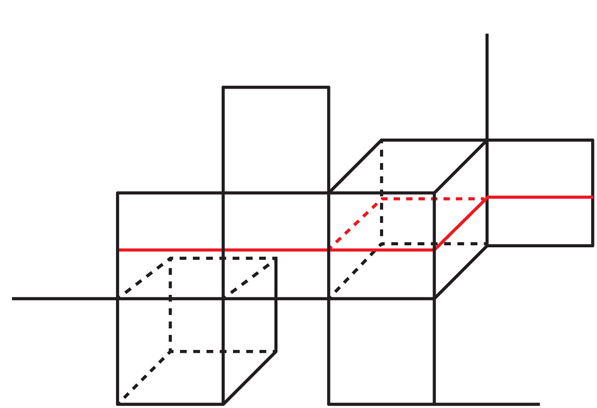
Fig.10. The red hyperplane in the rightmost square extends in a unique way to the hyperplane in the whole cubic complex.

This quality contrasts strongly with 3-varieties, in which a small part of the surface can be extended to the entire surface in a variety of ways. QC with its GP is “beautiful, crystal clear and strict,” says Eigol, and they do not have the “flabbiness” of 3-manifolds and their surfaces.

When we expand the GP in KK, it may stumble upon that cube with which it all began, and pass through it perpendicular to the initial GP (see Fig.11). In other words, an extended GP will not necessarily be embedded. As in the case of surfaces inside 3-manifolds, one can ask if QC has a finite covering in which these self-intersecting GPs rise to embedded ones — this is the version of Haken’s virtual hypothesis for QC.


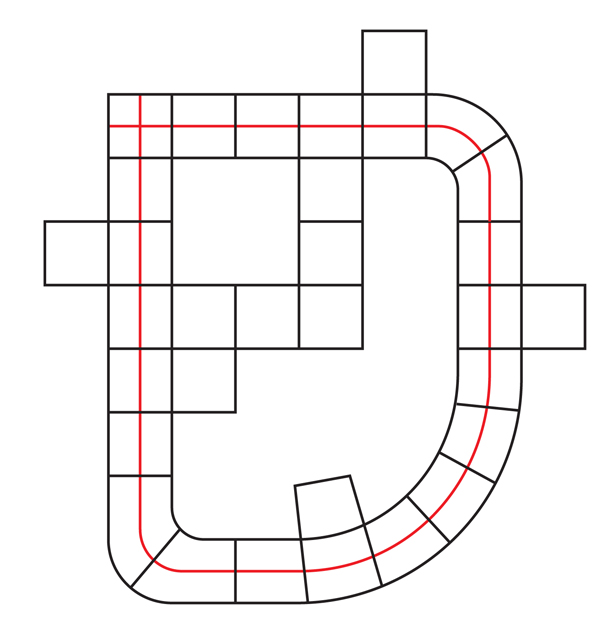
Figure 11

A few years ago, Wise and Frédéric Haglund from the University of Paris-South XI defined the class of “special” QCs, which, among other properties, have only embedded GPs. In the last decade, Wise developed an arsenal of techniques adapted to detect "special QC". In 2009, Wise released a 200-page “main job,” as Danfield called it, in which he described a set of discoveries related to special QCs, such as “combination theorems,” showing how to assemble special QCs together, to ensure that new QCs are guaranteed, also possessing "singularity." In his work, Wise formulated a hypothesis that, roughly speaking, any QC with a geometry that bends in a manner similar to a hyperbolic geometry is a “virtually” special — that is, it has a special final covering. This hypothesis was called the Wise hypothesis.

Wise was convinced that if a given form is in a certain way similar to QC - when it can be “cubed”, then the QC structure will be the key to discovering the many properties of the original form.

“QC was a secret that people didn’t even know what to ask,” he said. “This is a fundamental hidden structure.”

Cubic forests

Wise was extremely worried about the cubing of forms, but at first his colleagues laughed at him because of this mania.

Then Kahn and Markovic proved the incompressible surface theorem, and Vise and Bergeron immediately published a paper showing that the existence of incompressible surfaces in a compact hyperbolic 3-manifold gives a method for its cubing - and in such a way that the surfaces of the 3-manifold correspond exactly to the hyperplanes in the resulting cubic complex .

The key to the design of Vise and Bergeron was the fact that Kan and Markovich showed how to design not one, but many surfaces. Following the approach to cubing, first formulated in 2003 by Michael Sageyev, now working at Technion (Israel), Wise and Bergeron began by taking a huge collection of Kan-Markovich surfaces — enough to divide the 3-manifold into compact polygons.

Now let us imagine one of the intersection points of these surfaces - for example, there are n surfaces in it. The guesswork of Sageev was to consider this intersection as a shadow, so to speak, from the intersection of n hyperplanes in an n-dimensional cube. A QC corresponding to a 3-manifold is constructed, roughly speaking, by adding one n-dimensional cube for each intersection of n surfaces (in fact, all this is constructed more subtly to take into account different unforeseen topological circumstances). Two cubes in the complex are adjacent if their corresponding intersection points in a 3-manifold are connected by the face of one of the polyhedra.

“The cubic complex is needed to accurately calculate how the surfaces intersect with themselves and with each other,” says Danfield.

Vise and Bergeron showed that this QC is “homotopically equivalent” to the original manifold, that is, QC can be compressed and stretched (taking into account flattening in some dimensions and the reverse process) until QC turns into a variety, and vice versa. Moreover, this homotopic equivalence transforms each surface of a 3-manifold into a corresponding homotopically equivalent GP in KK.

A QC constructed in this way satisfies the geometric requirements of the Wise hypothesis, which means that if the Wise hypothesis is true, then this QC has a finite covering in which all GPs will be embedded.

If such a final covering really exists (say, covering m sheets), then you need to remember that you can build a covering from the CC itself, cutting it in a special way, then making m copies of this CC and gluing them together along the cuts. It is easy to show that this recipe for manufacturing a coating can be transferred to the production of a final coating of a 3-manifold, and that in this final coating the Cahn-Markovic surfaces used to construct QC will rise to the embedded surfaces. In other words, if the Wise’s hypothesis is true, then the SHQ is also true.

“This is a very strange compromise: your QC may be, for example, 10,000-dimensional, and it may seem to you that in some sense you worsen the situation,” says Wise. - But even despite the magnitude of QC, many of its properties are very easy to understand, so this procedure is very valuable. We prefer something big, but well organized, instead of a 3-manifold. ”

Even after Vise and Bergeron had established a connection between QA and HGH, most topologists studying 3-manifolds kept away from QC. Perhaps because Wise's 200-page work was discouraging, or because CC was so different from the spaces they were used to.

“These ideas were too esoteric for people who came out of hyperbolic geometry,” says Bergeron.

But one mathematician was already well versed in both the topology of 3-manifolds and the more abstract combinatorial things used by Wise in his approach.

“I think Ian Eigol was the only specialist on 3-varieties who understood quite early on how Vise's ideas could be used for the topology of 3-varieties,” says Bergeron.

Eigol deepened into the study of the “main work” of Vise and made sure that all its parts relating to the Vise hypothesis were correct. Aigol has been involved in the Supreme Committee for some time; he realized that the Vise approach, which had turned flabby surfaces into crystalline hyperplanes, was exactly what he needed.

“QC gives us scaffolding for the construction of the final covering,” he said.

To build a special end coat on the Wise-Bergeron QC, Eigol began to cut the QC along the GP into “Lego cubes”. He then assigned colors to the faces of the blocks, so that any two faces that meet on the corner have different colors. Then, Eigol showed that, roughly speaking, there is a way to glue a finite number of copies of Lego cubes along faces with the same colors in such a way that the colors on the sides of these faces will also coincide. As a result, each expanded GP will be one color. The resulting QC will be the final covering of the initial one, and all its GPs will be embedded, since any two intersecting GPs will be of a different color, so this will not be one GP that intersects itself.

On March 12, Eigol announced the proof of the Wise hypothesis and, consequently, the Hacken virtual hypothesis.

“It was the most exciting news since Perelman proved the geometrization hypothesis,” said Danfield.

Information passed through the community of 3-manifold researchers, and QC immediately became a common theme for all topologists.

“I think that until now the mathematical community has not understood how powerful Vise’s work is,” said Eigol. “I think that my result will explain to people what amazing progress it has achieved.”

Now, according to Vise, mathematicians are beginning to understand that "every time you cub up something, you will be able to uncover all sorts of secrets of the structure."

End of an era

Eigol's proof of Wise's theory was evidence of “4 for the price of 1”: it proved not only the UGH, but also the other three of the 23 Thurston questions that had remained open until then. During the time preceding the proof, Eigol and other mathematicians showed that all these three questions — the virtual bundle hypothesis and two more technical questions about hyperbolic 3-manifolds — also flowed out of the Wise hypothesis.

In the case of the hypothesis of a virtual bundle, we recall that the goal was to show that every compact hyperbolic 3-manifold has a finite covering stratified in a circle, that is, constructed by gluing opposite parts of a thickened surface. From the CGD, we know that the manifold has a finite Hacken cover - that is, the cover has a built-in incompressible surface. If you open the Haken variety along this surface, you will get something that looks like a thickened surface at the ends, but how God knows what is in the “guts”.


Ian Eigol on a recent trip to Daejeon, South Korea.

In 2008, according to Kalegari, an “amazing breakthrough” occurred, when Eigol showed that hyperbolic 3-manifolds that satisfy special technical conditions are guaranteed to be virtually stratified. The following year, Wise showed on this basis that all Haken varieties are virtually stratifying. That is, there is a way to expand the Haken manifold to obtain a finite cover that reveals a complex topology and leads to a simple layered manifold. Therefore, if the variety is virtually Haken, it must be virtually stratified.

“I think everyone believed that the CGT would be correct, but the virtual bundle hypothesis seemed to us less accessible,” Kalegari said. “For me, the fact that the virtual bundle hypothesis follows from the HCA is one of the most shocking sides of this whole story.”

With the proof of the virtual bundle hypothesis, "you may be tempted and decide that the 3-manifolds are too simple because the varieties stratified in a circle are simple," Minsky said. “But I think it teaches us that the varieties stratifying in a circle are not at all simple, and more cunning than we expected.”

At the same time, the virtual bundle theorem means that there is a simple and informative recipe for creating all compact hyperbolic 3-manifolds: start with a thickened surface, merge its inner and outer bound together with turns to your liking, and fold the manifold onto yourself a finite number of times.

“If you asked me for a hyperbolic 3-manifold, I would ask what type you need - what type of bundle and final covering? - says Kalegari. “Now we know that in this process we are not missing a single 3-manifold.”

And although mathematicians will need time to thoroughly test the work of Aigol, many of them are optimistic that it will pass the test.

“Ian Eigol is not a careless person,” says Minsky.

Now that, apparently, the last question from the Thurston list is resolved, researchers are beginning to wonder what the topology of 3-manifolds will look like in a wondrous new world after Thurston.

Mathematicians agree that they will have a lot of work with finding useful things that QC can offer for cubable forms. And for the 3-manifolds themselves, according to Aigol, the end of an era has come - and the beginning of the next one.

"In most areas of mathematics there is no plan that could outline a path for 20-30 years ahead, as we had it," he says. Now, he suggests, the topology of 3-manifolds and geometry may become similar to other areas of mathematics, in which scientists go to the touch and make progress even without such luxury as a large hypothetical picture of what is happening.

“New generations of mathematicians will come up with the following important questions,” says Eigol.