Neural networks and deep learning, chapter 3, part 1: improving the way neural networks are trained

When a person learns to play golf, he usually spends most of his time staging a basic hit. He then approaches other blows, gradually, studying these or those tricks, based on the basic blow and developing it. Similarly, we have so far focused on understanding the backpropagation algorithm. This is our “basic strike”, the basis for training for most of the work with neural networks (NS). In this chapter, I will talk about a set of techniques that can be used to improve our simpler implementation of backpropagation, and to improve the way of teaching NS.

Among the techniques that we will learn in this chapter are: the best option for the role of the cost function, namely the cost function with cross entropy; four so-called regularization methods (regularization of L1 and L2, exclusion of neurons [dropout], artificial extension of training data), which improve the generalizability of our NS beyond the limits of training data; best method for initializing network weights; a set of heuristic methods to help you choose good hyperparameters for the network. I will also consider several other techniques, a little more superficially. For the most part, these discussions are independent of each other, so you can jump over them if you wish. We also implement many technologies in the working code and use them to improve the results obtained for the task of classifying handwritten numbers, which was studied in Chapter 1.

Of course, we consider only a fraction of the huge number of techniques developed for use with neural networks. The bottom line is that the best way to enter the world of abundance of available techniques is to study in detail a few of the most important ones. Mastering these important techniques is not only useful in itself, it will also deepen your understanding of the problems that may arise when using neural networks. As a result, you will be prepared to quickly adapt new techniques as needed.

Cross Entropy Cost Function

Most of us hate being wrong. Shortly after starting to learn the piano, I gave a small concert in front of an audience. I was nervous, and began to play a piece an octave lower than necessary. I was confused, and could not continue until someone pointed out a mistake to me. I was very ashamed. However, although this is unpleasant, we also learn very quickly, deciding that we were wrong. And certainly the next time I spoke to the audience, I played in the right octave! Conversely, we learn more slowly when our mistakes are not well defined.

Ideally, we expect our neural networks to learn quickly from their mistakes. Does this happen in practice? To answer this question, let's look at a far-fetched example. It involves a neuron with just one input:



We are teaching this neuron to do something ridiculously simple: accept 1 and give 0. Of course, we could find a solution to such a trivial problem by manually selecting the weight and offset, without using the training algorithm. However, it will be quite useful to try using gradient descent to get weight and displacement as a result of training. Let's look at how a neuron is trained.

For definiteness, I will choose an initial weight of 0.6 and an initial offset of 0.9. These are some general values ​​assigned as a starting point, and I did not select them specifically. Initially, an output neuron produces 0.82, so we need to learn a lot to get close to the desired output of 0.0. In the original articleThere is an interactive form on which you can click “Run” and observe the learning process. This animation is not pre-recorded, the browser actually calculates the gradient, and then uses it to update the weight and offset, and shows the result. The learning speed is η = 0.15, slow enough to be able to see what is happening, but fast enough for learning to take place in seconds. The cost function C is quadratic, introduced in the first chapter. I will soon remind you of its exact form, so it is not necessary to come back and rummage there. Training can be started several times by simply clicking on the “Run” button.

As you can see, the neuron quickly learns the weight and bias, which lower the cost, and gives an output of 0.09. This is not quite the desired result of 0.0, but quite good. Suppose we choose an initial weight and offset of 2.0 instead. In this case, the initial output will be 0.98, which is completely wrong. Let's see how in this case the neuron will learn to produce 0.

Although this example uses the same learning rate (η = 0.15), we see that learning is slower. About 150 of the first epochs, weights and displacements hardly change. Then the training accelerates, and, almost as in the first example, the neuron moves rapidly to 0.0. this behavior is strange, not like learning a person. As I said at the beginning, we often learn most quickly when we are very mistaken. But we just saw how our artificial neuron learns with great difficulty, making a lot of mistakes - much harder than when he made a little mistake. Moreover, it turns out that such behavior arises not only in our simple example, but also in a more general purpose NS. Why is learning so slow? Can I find a way to avoid this problem?

To understand the source of the problem, we recall that our neuron learns through changes in weight and displacement at a rate determined by the partial derivatives of the cost function, ∂C / ∂w and ∂C / ∂b. So to say “learning is slow” is the same as saying that these partial derivatives are small. The problem is to understand why they are small. To do this, let's calculate the partial derivatives. Recall that we use the quadratic cost function, which is given by equation (6):

$$

where a is the neuron output when x = 1 is used at the input, and y = 0 is the desired output. To write this directly through weight and displacement, recall that a = σ (z), where z = wx + b. Using the chain rule for differentiation by weight and displacement, we obtain:

$$

$$

where I substituted x = 1 and y = 0. To understand the behavior of these expressions, let's take a closer look at the term σ '(z) on the right. Recall the shape of the sigmoid:



It can be seen from the graph that when the neuron output is close to 1, the curve becomes very flat and σ '(z) becomes small. Equations (55) and (56) tell us that ∂C / ∂w and ∂C / ∂b become very small. Hence the slowdown in learning. Moreover, as we will see a little later, the slowdown of training occurs, in fact, for the same reason and in the National Assembly of a more general nature, and not only in our simplest example.

Introducing Cross Entropy Cost Function

What do we do with slowing down learning? It turns out that we can solve the problem by replacing the quadratic function of value with another function of value, known as cross-entropy. To understand cross entropy, we move away from our simplest model. Suppose we train a neuron with several input values ​​x ₁ , x ₂ , ... corresponding weights w ₁ , w ₂ , ... and offset b:



The output of the neuron, of course, will be a = σ (z), where z = ∑ _j w _j x _j + b is the weighted sum of inputs. We define the cross-entropy cost function for a given neuron as

$$

where n is the total number of units of training data, the sum goes over all training data x, and y is the corresponding desired output.

It is not obvious that equation (57) solves the problem of slowing down learning. Honestly, it’s not even obvious that it makes sense to call it a function of value! Before turning to the slowdown in learning, let us see in what sense cross-entropy can be interpreted as a function of value.

Two properties in particular make it reasonable to interpret cross-entropy as a function of value. Firstly, it is greater than zero, that is, C> 0. To see this, note that (a) all the individual members of the sum in (57) are negative, since both logarithms are taken from numbers in the range from 0 to 1, and (b) the minus sign is in front of the sum.

Secondly, if the real output of the neuron is close to the desired output for all training inputs x, then the cross entropy will be close to zero. To prove this, we will need to assume that the desired outputs y will be either 0 or 1. Usually this happens when solving classification problems, or computing Boolean functions. To understand what happens if you do not make such an assumption, refer to the exercises at the end of the section.

To prove this, imagine that y = 0 and a≈0 for for some input x. So it will be when the neuron handles such an input well. We see that the first term of expression (57) for the value disappears, since y = 0, and the second will be −ln (1 − a) ≈0. The same is true when y = 1 and a≈1. Therefore, the contribution of value will be small if the real output is close to the desired.

Summing up, we get that the cross entropy is positive, and tends to zero when the neuron better calculates the desired output y for all training inputs x. We expect the presence of both properties in the cost function. And indeed, both of these properties are fulfilled by the quadratic value. Therefore, for cross-entropy is good news. However, the cross-entropy cost function has an advantage because, unlike the quadratic value, it avoids the problem of slowing down learning. To see this, let's calculate the partial derivative of value with cross entropy by weight. Substitute a = σ (z) in (57), apply the chain rule twice, and obtain

$$

$$

Reducing to a common denominator and simplifying, we get:

$$

Using the definition of sigmoid, σ (z) = 1 / (1 + e ^−z ) and a bit of algebra, we can show that σ ′ (z) = σ (z) (1 - σ (z)). I will ask you to verify this in the exercise further, but for now, accept it as the truth. The terms σ (z) and σ (z) (1 − σ (z)) are canceled, and this leads to

$$

Great expression. It follows from this that the speed with which weights are trained is controlled by σ (z) −y, i.e., by an error at the output. The larger the error, the faster the neuron learns. This could be expected intuitively. This option avoids the slowdown in learning caused by the term σ '(z) in a similar quadratic cost equation (55). When we use cross entropy, the term σ '(z) is reduced and we no longer have to worry about its smallness. This reduction is a special miracle guaranteed by the cross-entropy cost function. In fact, of course, this is not quite a miracle. As we will see later, cross entropy was specifically chosen for this property.

Similarly, the partial derivative for the bias can be calculated. I won’t give all the details again, but you can easily check that

$$

This again helps to avoid learning retardation due to the term σ '(z) in a similar equation for the quadratic value (56).

Exercise

• Check that σ ′ (z) = σ (z) (1 - σ (z)).

Let's go back to our far-fetched example that we played with earlier and see what happens if we use cross entropy instead of the quadratic value. To tune in, we start with the case in which the quadratic cost worked perfectly when the initial weight was 0.6 and the offset was 0.9. The original article has an interactive form in which you can click the Run button and see what happens when you replace the quadratic value with cross entropy.

Not surprisingly, the neuron in this case is trained perfectly, as before. Now let's look at the case in which the neuron used to get stuck , with weight and displacement starting at 2.0.



Success! This time the neuron learned quickly, as we wanted. If you look closely, you can see that the slope of the cost curve is initially steeper compared to the flat region of the corresponding quadratic value curve. This cross-country entropy gives us this coolness, and it doesn’t let us get stuck where we expect the fastest training of a neuron when it starts with very big mistakes.

I did not say what speed of training was used in the last examples. Earlier, with a quadratic value, we used η = 0.15. Should we use the same speed in the new examples? In fact, changing the cost function, it is impossible to say exactly what it means to use the “same” speed of learning; it will be a comparison of apples with oranges. For both cost functions, I experimented by looking for a learning speed that allows me to see what is happening. If you are still interested, then in the latest examples, η = 0.005.

You may argue that changing the speed of learning makes the graphics meaningless. Who cares how fast a neuron learns if we can arbitrarily choose a learning speed? But this objection does not take into account the main point. The meaning of the graphs is not in the absolute speed of learning, but in how this speed changes. When using the quadratic function, training is slower if the neuron is very wrong, and then it goes faster when the neuron approaches the desired answer. With cross-entropy, learning is faster when a neuron makes a big mistake. And these statements do not depend on a given learning speed.

We examined cross entropy for one neuron. However, this is easy to generalize to networks with many layers and many neurons. Assume that y = y ₁ , y ₂, ... are the desired values ​​of the output neurons, that is, the neurons in the last layer, and a ^L ₁ , a ^L ₂ , ... are the output values ​​themselves. Then cross entropy can be defined as:

$$

This is the same as equation (57), only now our ∑ _j sums over all output neurons. I will not analyze the derivative in detail, but it is reasonable to assume that using expression (63) we can avoid slowdown in networks with many neurons. If interested, you can take the derivative in the problem below.

Incidentally, the term “cross entropy” I use confused some early readers of the book because it contradicts other sources. In particular, often the cross entropy is determined for two probability distributions, pj
and qj, as ∑ _j p _j lnq _j. This definition can be associated with (57), if one sigmoid neuron is considered to give out a probability distribution consisting of activation of neuron a and 1-a value complementary to it.

However, if we have many sigmoid neurons in the last layer, the vector a ^L _j usually does not give a probability distribution. As a result, the definition of the type ∑ _j p _j lnq _jmeaningless, since we do not work with probability distributions. Instead (63), one can imagine how a summed set of cross-entropies of each neuron is summarized, where the activation of each neuron is interpreted as part of a two-element probability distribution (of course, there are no probability elements in our networks, so these are actually not probabilities). In this sense, (63) will be a generalization of cross entropy for probability distributions.

When to use cross entropy instead of quadratic value? In fact, cross entropy will almost always be used better if you have sigmoid output neurons. To understand this, remember that when setting up a network, we usually initialize weights and offsets using a random process. It may happen that this choice leads to the fact that the network will completely misinterpret some training input data - for example, the output neuron will tend to 1, when it should go to 0, or vice versa. If we use a quadratic value that slows down training, it will not stop training at all, since weights will continue to be trained on other training examples, but this situation is obviously undesirable.

Exercises

• One catch of cross-entropy is that at first it can be difficult to remember the corresponding roles of y and a. It is easy to get confused, as it will be correct, - [ylna + (1 − y) ln (1 − a)] or - [alny + (1 − a) ln (1 − y)]. What will happen to the second expression when y = 0 or 1? Does this problem affect the first expression? Why?
• In the discussion of a single neuron at the beginning of the section, I said that cross entropy is small if σ (z) ≈y for all training input data. The argument was based on the fact that y is 0 or 1. Usually it is in classification problems, but in other problems (for example, regression) y can sometimes take values ​​between 0 and 1. Show that the cross entropy is minimized anyway when σ (z) = y for all training inputs. When this happens, the value of cross entropy is

  $$

  . The value - [ylny + (1 − y) ln (1 − y)] is sometimes called binary entropy.

Tasks

• Multilayer networks with many neurons. In the entry in the last section, show that for the quadratic value, the partial derivative with respect to the weights in the output layer is

  $$

  The term σ '(z ^L _j ) causes learning to slow down when the neuron inclines to the wrong value. Show that for the cost function with cross entropy, the output error δ ^L for one training example x is given by the equation

  $$

  Use this expression to show that the partial derivative with respect to the weights in the output layer is given by the equation

  $$

  The term σ '(z ^L _j ) has disappeared, so cross entropy avoids the problem of slowing down learning, not only when used with one neuron, but also in networks with many layers and many neurons. With a slight change, this analysis is also suitable for biases. If this is not obvious to you, you should do this analysis as well.
• Using quadratic value with linear neurons in the outer layer. Let's say we have a multilayer network with many neurons. Suppose that in the final layer all neurons are linear, that is, the sigmoid activation function is not used, and their output is simply determined as a ^L _j = z ^L _j . Show that when using the quadratic cost function, the output error δL for one training example x is given

  $$

  Как и в прошлой задаче, используйте это выражение, чтобы показать, что частные производные по весам и смещениям во внешнем слое определяются, как

  $$

  $$

  Это показывает, что если выходные нейроны линейные, тогда квадратичная стоимость не вызовет никаких проблем с замедлением обучения. В этом случае квадратичная стоимость вполне подходит для использования.

Использование перекрёстной энтропии для классификации цифр из MNIST

Cross entropy is easy to implement as part of a program that teaches the network using gradient descent and back propagation. We will do this later by developing an improved version of our early handwritten numeric classification program from MNIST, network.py. The new program is called network2.py, and includes not only cross entropy, but also several other techniques developed in this chapter. In the meantime, let's see how well our new program classifies the MNIST digits. As in Chapter 1, we will use a network with 30 hidden neurons, and a mini-packet of size 10. We will set the learning speed η = 0.5 and we will learn 30 eras.

As I already said, it is impossible to say exactly what speed of training is suitable in which case, so I experimented with the selection. True, there is a way to very roughly heuristically relate the learning rate to cross entropy and quadratic value. We saw earlier that in the terms of the gradient for the quadratic value there is an additional term σ '= σ (1-σ). Suppose we average these values ​​for σ, ∫ ¹ ₀ dσ σ (1 − σ) = 1/6. It can be seen that the (very roughly) quadratic cost on average learns 6 times slower for the same learning rate. This suggests that a good starting point is to divide the learning speed for a quadratic function by 6. Of course, this is not at all a strict argument, and you should not take it too seriously. But it can sometimes be useful as a starting point.

The interface for network2.py is slightly different from network.py, but it should still be clear what is happening. The documentation on network2.py can be obtained using the help command (network2.Network.SGD) in the python shell.

>>> import mnist_loader
>>> training_data, validation_data, test_data = \
... mnist_loader.load_data_wrapper()
>>> import network2
>>> net = network2.Network([784, 30, 10], cost=network2.CrossEntropyCost)
>>> net.large_weight_initializer()
>>> net.SGD(training_data, 30, 10, 0.5, evaluation_data=test_data,
... monitor_evaluation_accuracy=True)

Note, by the way, that the net.large_weight_initializer () command is used to initialize weights and offsets in the same way as described in chapter 1. We need to run it because we will change the initialization of weights by default later. As a result, after starting all the above commands, we get a network that works with an accuracy of 95.49%. This is very close to the result from the first chapter, 95.42%, using the quadratic value.

Let's also look at the case where we use 100 hidden neurons and cross entropy, and leave the rest the same. In this case, the accuracy is 96.82%. This is a major improvement over the results from the first chapter, where we achieved accuracy of 96.59% using the quadratic value. The change may seem small, but think that the error fell from 3.41% to 3.18%. That is, we have eliminated approximately 1/14 errors. This is pretty good.

It is pretty nice that the cross-entropy cost function gives us similar or better results compared to the quadratic value. However, they do not unequivocally prove that cross entropy is the best choice. The fact is that I did not try to choose hyperparameters at all - the speed of training, the size of the mini-package, etc. In order to make the improvement more convincing, we need to properly tackle their optimization. But the results are still inspirational, and our theoretical calculations confirm that cross entropy is a better choice than the quadratic cost function.

In this vein, this entire chapter and, in principle, the rest of the book will go through. We will develop new technology, test it, and get "improved results." Of course, it’s good that we see these improvements. But interpreting them is always difficult. It will only be convincing if we see improvements after serious work on optimizing all other hyperparameters. And this is a rather complicated job, requiring large computational resources, and usually we will not deal with such a thorough investigation. Instead, we will go further on the basis of informal tests, such as those listed above. But you need to keep in mind that such tests are not unambiguous evidence, and carefully monitor those cases when the arguments begin to fail.

So far, we have been discussing cross entropy in detail. Why waste so much effort if it gives such a small improvement in our MNIST results? Later in this chapter we will see other techniques - in particular, regularization - which give much stronger improvements. So why do we focus on cross entropy? In particular, because cross entropy is a frequently used function of value, so it’s worth a good understanding. But the more important reason is that the saturation of neurons is an important problem in the field of neural networks, to which we will constantly return throughout the book. Therefore, I discussed cross entropy in such detail, since it is a good laboratory to begin to understand the saturation of neurons and how to approach approaches to this problem.

Что означает перекрёстная энтропия? Откуда она берётся?

Our discussion of cross entropy revolved around algebraic analysis and practical implementation. This is useful, but as a result, broader conceptual questions remain unanswered, for example: what does cross entropy mean? Is there an intuitive way to present it? How could people even come up with cross entropy?

Let's start with the last: what could make us think about cross entropy? Suppose we discovered a learning slowdown described earlier and realized that it was caused by the terms σ '(z) in equations (55) and (56). Having a little glance at these equations, we could think about whether it is possible to choose such a cost function so that the term σ '(z) disappears. Then the cost C = C _{x of} one training example would satisfy the equations:

$$

$$

If we chose a value function that makes them true, then they would rather simply describe an intuitive understanding that the larger the initial error, the faster the neuron learns. They would also fix the slowdown problem. In fact, starting with these equations, we would show that it is possible to derive the form of cross entropy by simply following a mathematical instinct. To see this, we note that, based on the chain rule, we get:

$$

Using in the last equation σ ′ (z) = σ (z) (1 − σ (z)) = a (1 − a), we obtain:

$$

Comparing with equation (72), we obtain:

$$

Integrating this expression over a, we get:

$$

This is the contribution of a separate training example x to the cost function. To get the full cost function, we need to average over all the training examples, and we come to:

$$

The constant here is the average of the individual constants of each of the training examples. As you can see, equations (71) and (72) uniquely determine the shape of cross entropy, flesh to a common constant. Cross entropy was not magically taken out of thin air. She could be found in a simple and natural way.

What about the intuitive idea of ​​cross entropy? How do we imagine it? A detailed explanation would lead us to overtake our training course. However, we can mention the existence of a standard way of interpreting cross entropy, originating from the field of information theory. Roughly speaking, cross entropy is a measure of surprise. For example, our neuron is trying to calculate the function x → y = y (x). But instead, it counts the function x → a = a (x). Suppose we imagine a as a neuron’s estimate of the probability that y = 1, and 1-a is the probability that the correct value for y is 0. Then cross entropy measures how much we are “surprised” on average when find the true value of y. We are not very surprised if we expect a way out, and we are very surprised if the way out is unexpected. Of course, I did not give a strict definition of "surprise", so all this can seem like empty rant. But in fact, in the theory of information there is an exact way to determine unexpectedness. Unfortunately, I am not aware of any examples of a good, short and self-sufficient discussion of this point on the Internet. But if you are interested in digging deeper, thenThe Wikipedia article has good general information that will send you in the right direction. Details can be found in Chapter 5 on Kraft inequality in a book on information theory .

Task

• We have discussed in detail the slowdown in learning that can occur when neurons are saturated in networks using the quadratic cost function in learning. Another factor that can inhibit learning is the presence of the term x _j in equation (61). Because of it, when the output x _j approaches zero, the corresponding weight w _j will be trained slowly. Explain why it is impossible to eliminate the term x _{j by} choosing some ingenious cost function.

Softmax (soft maximum function)

In this chapter, we will mostly use the cross-entropy cost function to solve the problems of slowing down learning. However, I would like to briefly discuss another approach to this problem, based on the so-called softmax-layers of neurons. We will not use Softmax layers for the remainder of this chapter, so if you are in a hurry, you can skip this section. However, Softmax is still worth understanding, in particular because it is interesting in itself, and in particular because we will use Softmax layers in Chapter 6, in our discussion of deep neural networks.

The idea of ​​Softmax is to define a new type of output layer for HC. It begins in the same way as the sigmoid layer, with the formation of weighted inputs$$. However, we do not use a sigmoid to get an answer. In the Softmax layer, we apply the Softmax function to z ^L _j . According to her, the activation a ^L _{j of the} output neuron No. j is equal to:

$$

where in the denominator we sum over all output neurons.

If the Softmax function is unfamiliar to you, equation (78) will seem mysterious to you. It is not at all obvious why we should use such a function. It is also not obvious that it will help us solve the problem of slowing down learning. To better understand equation (78), suppose we have a network with four output neurons and four corresponding weighted inputs, which we will designate as z ^L ₁ , z ^L ₂ , z ^L ₃ and z ^L ₄ . In the original articleThere are interactive adjustment sliders that are assigned the possible values ​​of the weighted inputs and a schedule of the corresponding output activations. A good starting point to study them would be to use the bottom slider to increase z ^L ₄ .





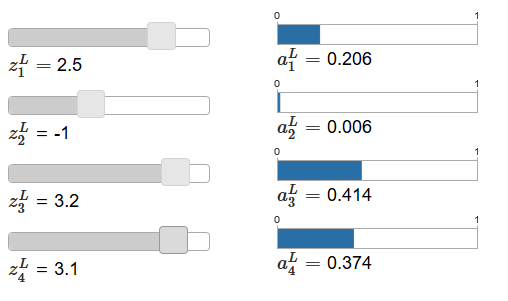
By increasing z ^L ₄ , one can observe an increase in the corresponding output activation, a ^L ₄ , and a decrease in other output activations. With decreasing z ^L ₄ a ^L ₄ will decrease, and all other output activations will increase. Having looked closely, you will see that in both cases the general change in other activations exactly compensates for the change that occurs in a ^L ₄. The reason for this is the guarantee that all output activations in total give 1, which we can prove using equation (78) and some algebra:

$$

As a result, with an increase in a ^L _{4, the} remaining output activations must decrease by the same value in total to ensure that the sum of all output activations is equal to 1. And, of course, similar statements will be true for all other activations.

It also follows from equation (78) that all output activations are positive, since the exponential function is positive. Combining this with the observation from the previous paragraph, we find that the output of the Softmax layer will be a set of positive numbers giving a total of 1. In other words, the output of the Softmax layer can be represented as a probability distribution.

The fact that the output of the Softmax layer is a probability distribution is very pleasant. In many problems it is convenient to be able to interpret the output activations a ^L _jas an estimate by the network of the likelihood that the correct variant will be j So, for example, in the classification problem MNIST, we can interpret a ^L _j as an estimate by the network of the probability that j will be the correct version of the classification of a digit.

Conversely, if the output layer was sigmoid, then we definitely cannot assume that activations form a probability distribution. I will not prove this strictly, but it is reasonable to assume that activations of the sigmoid layer in the general case do not form a probability distribution. Therefore, using a sigmoid output layer, we will not get such a simple interpretation of output activations.

Exercise

• Make an example showing that in a network with a sigmoid output layer, the output activations a ^L _j do not always add up to 1.

We begin to understand a bit about Softmax functions and how Softmax layers behave. Just to summarize: the exponents in equation (78) ensure that all output activations are positive. The sum in the denominator of equation (78) ensures that Softmax gives a total of 1. Therefore, this kind of equation no longer seems mysterious: this is a natural way to ensure that the output activations form a probability distribution. Softmax can be imagined as a way to scale z ^L _j and then compress them together to form a probability distribution.

Exercises

• Монотонность Softmax. Покажите, что ∂a^L_j / ∂z^L_k положительна, если j=k, и отрицательна, если j≠k. Как следствие, увеличение z^L_j гарантированно увеличивает соответствующую выходную активацию a^L_j, и уменьшает все остальные выходные активации. Мы уже видели это эмпирически на примере ползунков, однако данное доказательство будет строгим.
• Нелокальность Softmax. Приятной особенностью сигмоидных слоёв является то, что выход a^L_j — функция соответствующего взвешенного входа, a^L_j = σ(z^L_j). Поясните, почему с Softmax-слоем это не так: любая выходная активация a^L_j зависит от всех взвешенных входов.

Задача

• Инвертирование Softmax-слоя. Допустим, у нас есть НС с выходным Softmax-слоем и активации a^L_j известны. Покажите, что соответствующие взвешенные входы имеют форму z^L_j = ln a^L_j + C, где C – константа, не зависящая от j.

Проблема замедления обучения

We have already become quite familiar with Softmax layers of neurons. But so far we have not seen how Softmax layers allow us to solve the problem of slowing down learning. To understand this, let's define a cost function based on the “log-likelihood”. We will use x to denote the training input of the network, and y for the corresponding desired output. Then the LPS associated with this training input will be:

$$

So if, for example, we study on MNIST images, and image 7 went into the input, then the LPS will be −ln a ^L ₇ . To understand this intuitively, we consider the case when the network copes well with recognition, that is, it is sure that it is at input 7. In this case, it will evaluate the value of the corresponding probability a ^L ₇ as close to 1, therefore the cost −ln a ^L ₇ will be small . Conversely, if the network does not work well, then the probability of a ^L ₇ will be less, and the cost −ln a ^L ₇ will be more. Therefore, LPS behaves as expected from a cost function.

What about the slowdown problem? To analyze it, we recall that the main thing in deceleration is the behavior of ∂C / ∂w ^L _jk and ∂C / ∂b ^L _j . I will not describe in detail the capture of the derivative - I will ask you to do this in tasks, but using some algebra you can show that:

$$

$$

I've played a little with the notation here, and I'm using “y” a little differently than in the last paragraph. There, y denotes the desired network output — that is, if the output is “7”, then the input was image 7. And in these equations, y denotes the output activation vector corresponding to 7, that is, a vector with all zeros except unity in 7 th position.

These equations are the same as similar expressions that we obtained in an earlier analysis of cross entropy. Compare, for example, equations (82) and (67). This is the same equation, although the latter is averaged over training examples. And, as in the first case, these expressions guarantee that learning is not slowed down. It is useful to imagine that the output Softmax layer with LPS is quite similar to the layer with sigmoid output and cost based on cross entropy.

Given their similarity, what should be used - sigmoid output and cross entropy, or Softmax output and LPS? In fact, in many cases both approaches work well. Although later in this chapter we will use a sigmoid output layer with a cost based on cross entropy. Later, in chapter 6, we will sometimes use Softmax output and LPS. The reason for the changes is to make some of the following networks more similar to the networks found in some influential research papers. From a more general point of view, Softmax and LPS should be used when you need to interpret output activations as probabilities. This is not always necessary, but it can be useful in classification problems (such as MNIST), which include non-intersecting classes.

Tasks

• Derive equations (81) and (82).
• Откуда взялось название Softmax? Допустим, мы изменим Softmax-функцию так, чтобы выходные активации задавались уравнением

  $$

  где c – положительная константа. Отметим, что c = 1 соответствует стандартной Softmax-функции. Но используя другое значение c, мы получим другую функцию, которая качественно всё равно будет похожей на Softmax. Покажите, что выходные активации формируют распределение вероятности, как и в случае с обычной Softmax. Допустим, мы сделаем c очень большой, то есть c → &inf;. Какого ограничивающее значение выходных активаций a^L_j? После решения этой задачи должно быть ясно, почему функция с c = 1 считается «смягчённой версией» функции максимума. Отсюда и происходит термин softmax.
• Обратное распространение с Softmax и ЛПС. В прошлой главе мы вывели алгоритм обратного распространения для сети, содержащей сигмоидные слои. Чтобы применить этот алгоритм к сети и Softmax-слоями, нам надо вывести выражение для ошибки δ^L_j ≡ ∂C/∂z^L_j. Покажите, что подходящим выражением будет

  $$

  Исползуя это выражение, мы можем применить алгоритм обратного распространения к сети, используя выходной Softmax-слой и ЛПС.

Переобучение и регуляризация

The Nobel laureate Enrico Fermi was once asked for an opinion on the mathematical model proposed by several colleagues to solve an important unresolved physical problem. The model corresponded perfectly to the experiment, but Fermi was skeptical about it. He asked how many free parameters in it can be changed. “Four,” they told him. Fermi replied: “I remember how my friend Johnny von Neumann liked to say that with four parameters you can push an elephant there, and with five you can make him wave his trunk.”

The meaning of history, of course, is that models with a large number of free parameters can describe a surprisingly wide range of phenomena. Even if such a model works well with available data, it does not automatically make it a good model. It just might mean that the model has enough freedom to describe almost any data set of a given size without revealing the main idea of ​​the phenomenon. When this happens, the model works well with existing data, but cannot generalize the new situation. A true test of a model is its ability to make predictions in situations that it has not encountered before.

Fermi and von Neumann were suspicious of models with four parameters. Our NS with 30 hidden neurons for the classification of MNIST digits has almost 24,000 parameters! These are quite a few parameters. Our NS with 100 hidden neurons has almost 80,000 parameters, and advanced deep NSs of these parameters sometimes have millions or even billions. Can we trust the results of their work?

Let's complicate this problem by creating a situation in which our network poorly generalizes a new situation for it. We will use NS with 30 hidden neurons and 23,860 parameters. But we will not train the network with all 50,000 MNIST images. Instead, we use only the first 1000. Using a limited set will make the generalization problem more obvious. We will learn as before, using the cost function based on cross entropy, with a learning speed of η = 0.5 and a mini-packet size of 10. However, we will study 400 eras, which is slightly more than before, since there are training examples we don’t have much. Let's use network2 to look at how the cost function changes:

>>> import mnist_loader 
>>> training_data, validation_data, test_data = \
... mnist_loader.load_data_wrapper()
>>> import network2 
>>> net = network2.Network([784, 30, 10], cost=network2.CrossEntropyCost) 
>>> net.large_weight_initializer()
>>> net.SGD(training_data[:1000], 400, 10, 0.5, evaluation_data=test_data,
... monitor_evaluation_accuracy=True, monitor_training_cost=True)

Using the results, we can build a graph of the change in cost when training the network (graphs were made using the overfitting.py program):



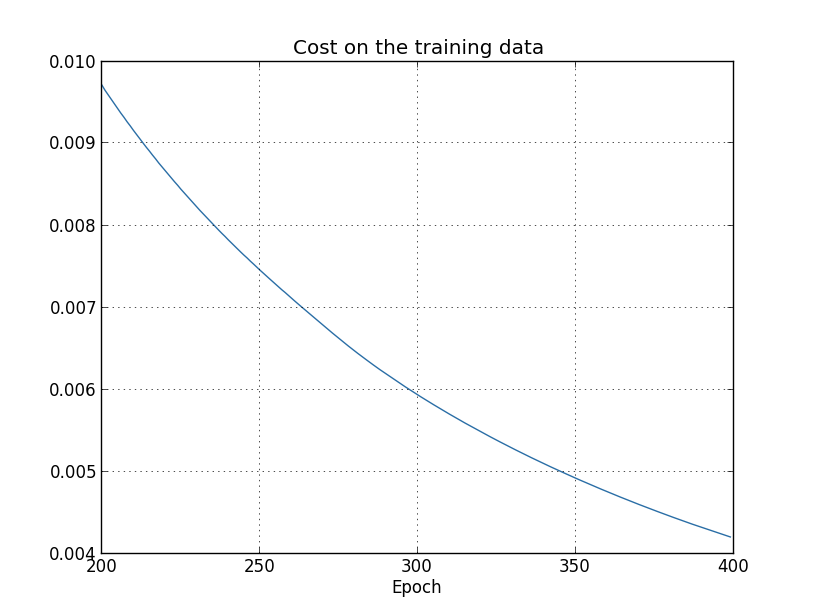
It looks encouraging, there is a smooth decrease in cost, as expected. Keep in mind that I showed only the epochs from 200 to 399. As a result, we see on an enlarged scale the late stages of training, at which, as we will see later, all the most interesting happens.

Now let's see how the classification accuracy on the verification data changes over time:



Then I again increased the schedule. In the first 200 eras, which are not visible here, accuracy increases to almost 82%. Then the training gradually slows down. Finally, around the 280th era, classification accuracy ceases to improve. In later eras, only small stochastic fluctuations are observed around the accuracy value achieved at the 280th epoch. Compare this to the previous chart, where the cost associated with training data is gradually decreasing. If you study only this cost, it will seem that the model is improving. However, the results of working with test data tell us that this improvement is just an illusion. As in the model that Fermi did not like, what our network studies after the 280th era is no longer generalized to verification data. Therefore, this training ceases to be useful. We say that after the 280th era, the network is retraining,

You may be wondering if it is not a problem that I am studying cost based on training data, and not on the accuracy of classification of verification data. In other words, perhaps the problem is that we are comparing apples with oranges. What will happen if we compare the cost of training data with the cost of verification, that is, we will compare comparable measures? Or perhaps we could compare the classification accuracy of both training and test data? In fact, the same phenomenon appears regardless of how the comparison is made. But the details are changing. For example, let's see the value of the verification data:



It can be seen that the cost of verification data improves until around the 15th era, and then begins to deteriorate altogether, although the cost of training data continues to improve. This is another sign of a retrained model. However, the question arises, what era should we consider the point at which retraining begins to prevail over training - 15 or 280? From a practical point of view, we are nevertheless interested in improving the accuracy of classification of verification data, and cost is just a mediator of the accuracy of classification. Therefore, it makes sense to consider the era of 280 a point, after which retraining begins to prevail over the training of our National Assembly.

Another sign of retraining can be seen in the accuracy of the classification of training data:



Accuracy is growing, reaching 100%. That is, our network correctly classifies all 1000 training images! Meanwhile, verification accuracy grows to only 82.27%. That is, our network only studies the features of the training set, and does not learn to recognize numbers at all. It seems that the network simply remembers the training set, not understanding the numbers well enough to generalize this to the test set.

Retraining is a serious problem of the National Assembly. This is especially true for modern NSs, which usually have a huge amount of weights and displacements. For effective training, we need a way to determine when retraining occurs so as not to retrain. And we would also like to be able to reduce the effects of retraining.

An obvious way to detect retraining is to use the approach above, monitor the accuracy of working with verification data during network training. If we see that the accuracy on the verification data is no longer improving, we must stop training. Of course, strictly speaking, this will not necessarily be a sign of retraining. Perhaps the accuracy of working with test and training data will stop improving at the same time. Yet applying such a strategy will prevent retraining.

And we will use a small variation of this strategy. Recall that when we load data into MNIST, we divide them into three sets:

>>> import mnist_loader 
>>> training_data, validation_data, test_data = \
... mnist_loader.load_data_wrapper()

So far we have used training_data and test_data, and ignored validation_data [confirming]. Validation_data contains 10,000 images, which differ from both 50,000 images of the MNIST training set and 10,000 images of the validation set. Instead of using test_data to prevent overfitting, we will use validation_data. To do this, we will use almost the same strategy that was described above for test_data. That is, we will calculate the classification accuracy of validation_data at the end of each era. Once the classification accuracy of validation_data is full, we will stop learning. This strategy is called an early stop. Of course, in practice, we will not be able to immediately find out that the accuracy is satiated. Instead, we will continue training until we make sure of this (and decide

Why use validation_data to prevent retraining rather than test_data? It is part of a more general strategy to use validation_data to evaluate different choices for hyperparameters — the number of epochs to learn, the speed of learning, the best network architecture, etc. We use these estimates to find and assign good values ​​to hyperparameters. And although I have not mentioned this yet, it was partly because of this that I made the choice of hyperparameters in the earlier examples in the book.

Of course, this remark does not answer the question of why we use validation_data, and not test_data, to prevent overfitting. It simply replaces the answer to a more general question - why do we use validation_data, and not test_data, to select hyperparameters? To understand this, keep in mind that when choosing hyperparameters, we most likely have to choose from a variety of their options. If we assign hyperparameters based on the ratings from test_data, we will probably tailor this data too much specifically for test_data. That is, we may find hyperparameters that are well suited to the specific features of specific data from test_data, however, the operation of our network will not be generalized to other data sets. We avoid this by selecting hyperparameters using validation_data. And then, having received the GP we need, we conduct a final accuracy assessment using test_data. This gives us confidence that our results with test_data are a true measure of the degree of generalization of the NS. In other words, supporting data is such special training data that helps us learn good GP. This approach to locating GPs is sometimes called the retention method, since validation_data is "held" separately from training_data.

In practice, even after evaluating the quality of work on test_data, we will want to change our mind and try a different approach - perhaps a different network architecture - which will include searches for a new set of GPs. In this case, is there a danger that we will unnecessarily adapt to test_data? Will we need a potentially infinite number of data sets so that we can be sure that our results are well generalized? In general, this is a deep and complex problem. But for our practical purposes, we will not worry too much about this. We simply dive headlong into further research using a simple retention method based on training_data, validation_data and test_data, as described above.

So far, we have been considering retraining using 1000 training images. What happens if we use a complete training set of 50,000 images? We will leave all other parameters unchanged (30 hidden neurons, learning speed 0.5, mini-packet size 10), but we will study 30 eras using all 50,000 pictures. Here is a graph that shows the accuracy of the classification on training data and test data. Note that here I used validation data rather than validation data to make it easier to compare the results with earlier graphs.



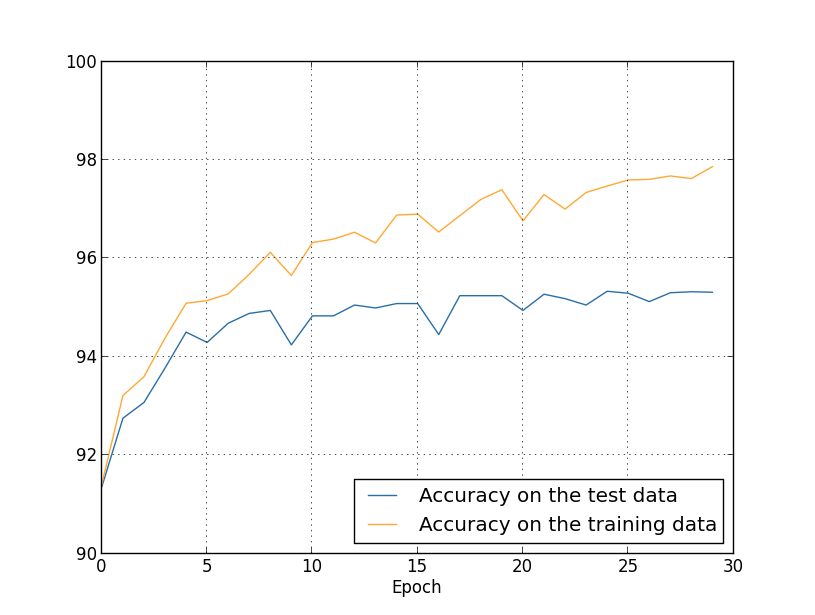
It can be seen that the accuracy indicators on the test and training data remain closer to each other than when using 1000 training examples. In particular, the best classification accuracy, 97.86%, is only 2.53% higher than 95.33% of the verification data. Compare with an early break of 17.73%! Retraining is taking place, but greatly reduced. Our network compiles information much better, moving from training to test data. In general, one of the best ways to reduce retraining is to increase the amount of training data. With enough training data, it's difficult to retrain even a very large network. Unfortunately, getting training data is expensive and / or difficult, so this option is not always practical.

Regularization

Increasing the amount of training data is one way to reduce retraining. Are there other ways to reduce retraining? One possible approach is to reduce network size. True, large networks have potential more than small ones, so we are reluctant to resort to this option.

Fortunately, there are other techniques that can reduce retraining, even when we have fixed the size of the network and training data. They are known as regularization techniques. In this chapter, I will describe one of the most popular techniques, sometimes called weakening weights, or regularizing L2. Her idea is to add an extra member called the regularization member to the cost function. Here is cross-entropy with regularization:

$$

The first term is a common expression for cross entropy. But we added a second, namely, the sum of the squares of all the network weights. It is scaled by the factor λ / 2n, where λ> 0 is the regularization parameter, and n, as usual, is the size of the training set. We will discuss how to choose λ. It is also worth noting that biases are not included in the regularization term. About it below.

Of course, it is possible to regularize other cost functions, for example, quadratic. This can be done in a similar way:

$$

In both cases, we can write the regularized cost function as

$$

where C ₀ is the original cost function without regularization.

It is intuitively clear that the point of regularization is to persuade the network to prefer smaller weights, all other things being equal. Large weights will be possible only if they significantly improve the first part of the cost function. In other words, regularization is a way of choosing a compromise between finding small weights and minimizing the initial cost function. It is important that these two elements of the compromise depend on the value of λ: when λ is small, we prefer to minimize the original cost function, and when λ is large, we prefer small weights.

It is not at all obvious why the choice of such a compromise should help reduce retraining! But it turns out it helps. We will figure out why it helps in the next section. But first, let's work with an example showing that regularization does reduce retraining.

To construct an example, we first need to understand how to apply the training algorithm with stochastic gradient descent to a regularized NS. In particular, we need to know how to calculate the partial derivatives, ∂C / ∂w and ∂C / ∂b for all weights and offsets in the network. After taking the partial derivatives in equation (87) we get:

$$

$$

The terms ∂C ₀ / ∂w and ∂C ₀ / ∂w can be calculated through the OP, as described in the previous chapter. We see that it is easy to calculate the gradient of the regularized cost function: you just need to use the OP as usual, and then add λ / nw to the partial derivative of all the weight terms. The partial derivatives with respect to displacements do not change, therefore, the rule of learning by gradient descent for displacements does not differ from the usual one:

$$

The training rule for weights turns into:

$$

$$

Everything is the same as in the usual gradient descent rule, except that we first scale the weight w by a factor of 1 - ηλ / n. This scaling is sometimes called weight loss, as it reduces weight. At first glance, it seems that the weights are irresistibly tending to zero. But this is not so, since the other term can lead to an increase in weights if this leads to a decrease in the irregular cost function.

Ok, let gradient descent work like this. What about stochastic gradient descent? Well, as in the irregularized version of stochastic gradient descent, we can estimate ∂C ₀ / ∂w through averaging over the mini-package of m training examples. Therefore, the regularized learning rule for stochastic gradient descent turns into (see equation (20)):

$$

where the sum goes for training examples x in the mini-package, and C _x is the irregular cost for each training example. Everything is the same as in the usual rule of stochastic gradient descent, with the exception of 1 - ηλ / n, the weight loss factor. Finally, to complete the picture, let me write down a regularized rule for offsets. Naturally, it is exactly the same as in the irregular case (see equation (21)):

$$

where the amount goes for training examples x in the mini-package.

Let's see how regularization changes the effectiveness of our National Assembly. We will use a network with 30 hidden neurons, a mini-packet of size 10, a learning speed of 0.5, and a cost function with cross entropy. However, this time we use the regularization parameter λ = 0.1. In the code, I named this variable lmbda, since the word lambda is reserved in python for things not related to our topic. I also used test_data again again instead of validation_data. But I decided to use test_data, because the results can be compared directly with our early, irregular results. You can easily change the code so that it uses validation_data and make sure that the results are similar.

>>> import mnist_loader 
>>> training_data, validation_data, test_data = \
... mnist_loader.load_data_wrapper() 
>>> import network2 
>>> net = network2.Network([784, 30, 10], cost=network2.CrossEntropyCost)
>>> net.large_weight_initializer()
>>> net.SGD(training_data[:1000], 400, 10, 0.5,
... evaluation_data=test_data, lmbda = 0.1,
... monitor_evaluation_cost=True, monitor_evaluation_accuracy=True,
... monitor_training_cost=True, monitor_training_accuracy=True)

The cost of training data is constantly decreasing, as in the earlier case, without regularization:



But this time, the accuracy on test_data continues to increase throughout all 400 epochs:



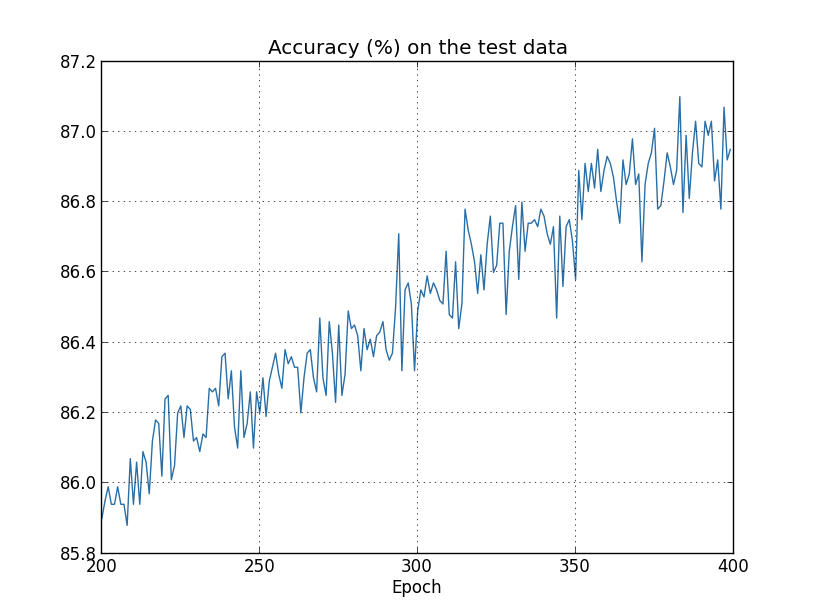
Obviously, regularization suppressed retraining. Moreover, the accuracy has increased significantly, and the peak classification accuracy reaches 87.1%, compared with the 82.27% peak achieved in the case without regularization. In general, we almost certainly achieve better results by continuing to study after 400 eras. Empirically, regularization seems to make our network better generalize knowledge, and significantly reduces the effects of retraining.

What happens if we leave our artificial environment, which uses only 1,000 teaching pictures, and return to the full set of 50,000 images? Of course, we have already seen that retraining is a much smaller problem with a full set of 50,000 images. Does regularization help to improve the result? Let's keep the previous values ​​of hyperparameters - 30 epochs, speed 0.5, mini-packet size 10. However, we need to change the regularization parameter. The fact is that the size n of the training set jumped from 1000 to 50 000, and this changes the weakening factor of weights 1 - ηλ / n. If we continue to use λ = 0.1, this would mean that weights are weakened much less, and as a result, the effect of regularization decreases. We compensate for this by accepting λ = 5.0.

Ok, let's train our network by first reinitializing the weights:

>>> net.large_weight_initializer()
>>> net.SGD(training_data, 30, 10, 0.5,
... evaluation_data=test_data, lmbda = 5.0,
... monitor_evaluation_accuracy=True, monitor_training_accuracy=True)

We get the results:



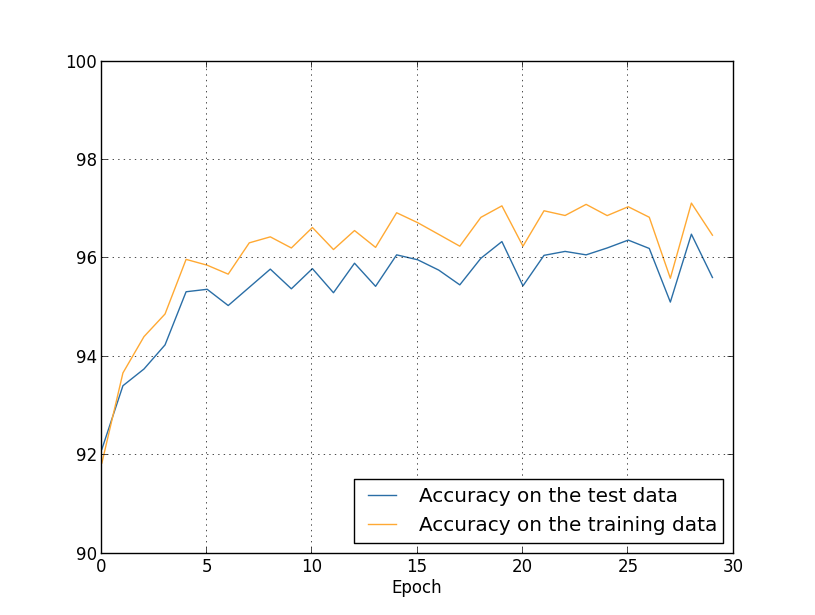
A lot of all pleasant things. Firstly, our classification accuracy on verification data has grown, from 95.49% without regularization to 96.49% with regularization. This is a major improvement. Secondly, it can be seen that the gap between the results of work on the training and test sets is much lower than before, less than 1%. The gap is still decent, but we obviously have made significant progress in reducing retraining.

Finally, see what classification accuracy we get when using 100 hidden neurons and the regularization parameter & lambda = 5.0. I will not give a detailed analysis of retraining, this is just for fun, to see how much accuracy can be achieved with our new tricks: a cost function with cross entropy and regularization L2.

>>> net = network2.Network([784, 100, 10], cost=network2.CrossEntropyCost)
>>> net.large_weight_initializer()
>>> net.SGD(training_data, 30, 10, 0.5, lmbda=5.0,
... evaluation_data=validation_data,
... monitor_evaluation_accuracy=True)

The end result is a classification accuracy of 97.92% on supporting data. A big leap compared to the case with 30 hidden neurons. You can fine-tune a little more, start the process for 60 epochs with η = 0.1 and λ = 5.0, and overcome the barrier of 98%, reaching an accuracy of 98.04 on the supporting data. Not bad for 152 lines of code!

I described regularization as a way to reduce retraining and increase classification accuracy. But these are not its only advantages. Empirically, having tried our MNIST network through many launches, changing weights each time, I found that launches without regularization sometimes “stuck”, obviously falling into the local minimum of the cost function. As a result, different launches sometimes produced very different results. And regularization, on the contrary, allows you to get much easier reproducible results.

Why is this so? Heuristically, when the cost function does not have regularization, the length of the vector of weights will most likely grow, all other things being equal. Over time, this can lead to a very large vector of weights. And because of this, the vector of the scales can get stuck, showing in approximately the same direction, since changes due to gradient descent make only tiny changes in direction with a large length of the vector. I believe that because of this phenomenon, it is very difficult for our training algorithm to study the space of weights properly, and therefore it is difficult to find a good minimum of the cost function.