Neural networks and deep learning, chapter 1: using neural networks to recognize handwritten numbers

Note

Here is a translation of Michael Nielsen’s free online book Neural Networks and Deep Learning, distributed under the Creative Commons Attribution-NonCommercial 3.0 Unported License . The motivation for its creation was the successful experience of translating a programming textbook, Expressive JavaScript . The book on neural networks is also quite popular; authors of English-language articles actively cite it. I did not find her translations, except for the translation of the beginning of the first chapter with abbreviations .

Those who want to thank the author of the book can do this on its official page , by transfer via PayPal or Bitcoin. To support the translator on Habré there is a form "to support the author".

Introduction

This tutorial will tell you in detail about concepts such as:

• Neural networks - an excellent software paradigm, created under the influence of biology, and allowing the computer to learn based on observations.
• Deep learning is a powerful set of neural network training techniques.

Neural networks (NS) and deep learning (GO) today provide the best solution to many problems in the areas of image recognition, voice and natural language processing. This tutorial will teach you many of the key concepts that underpin NS and GO.

What is this book about

NS is one of the finest software paradigms ever invented by man. With a standard programming approach, we tell the computer what to do, break large tasks into many small ones, and precisely determine tasks that the computer will easily perform. In the case of the National Assembly, on the contrary, we do not tell the computer how to solve the problem. He himself learns this on the basis of "observations" of the data, "inventing" his own solution to the problem.

Automated data-based learning sounds promising. However, until 2006, we did not know how to train the National Assembly so that they could transcend the more traditional approaches, with the exception of a few special cases. In 2006, training techniques of the so-called deep neural networks (GNS). Now these techniques are known as deep learning (GO). They continued to be developed, and today GNS and GO have achieved amazing results in many important tasks related to computer vision, speech recognition, and natural language processing. On a large scale, they are being deployed by companies such as Google, Microsoft and Facebook.

The purpose of this book is to help you master the key concepts of neural networks, including modern GO techniques. After working with the tutorial, you will write a code that uses NS and GO to solve complex problems of pattern recognition. You will have a foundation for using NS and civil defense in the approach to solving your own problems.

Principle Based Approach

One of the beliefs underlying the book is that it is better to acquire a solid understanding of the key principles of the National Assembly and Civil Society than to grab knowledge from a long list of different ideas. If you have a good understanding of key ideas, you will quickly understand other new material. In the programmer’s language, we can say that we will study the basic syntax, libraries, and data structures of the new language. You may recognize only a small fraction of the entire language — many languages ​​have immense standard libraries — however, you can understand new libraries and data structures quickly and easily.

So, this book is categorically not educational material on how to use any particular library for the National Assembly. If you just want to learn how to work with the library - do not read the book! Find the library you need and work with training materials and documentation. But keep in mind: although this approach has the advantage of instantly solving the problem, if you want to understand what exactly is happening inside the National Assembly, if you want to master ideas that will be relevant in many years, then it will not be enough for you to simply study some kind of fashion library. You need to understand the reliable and long-term ideas underlying the work of the National Assembly. Technology comes and goes, and ideas last forever.

Practical approach

We will study the basic principles by the example of a specific task: teaching a computer to recognize handwritten numbers. Using traditional programming approaches, this task is extremely difficult to solve. However, we can solve it quite well with a simple NS and several dozen lines of code, without any special libraries. Moreover, we will gradually improve this program, consistently including in it more and more key ideas about the National Assembly and Civil Defense.

This practical approach means that you will need some programming experience. But you do not have to be a professional programmer. I wrote python code (version 2.7) that should be clear even if you haven't written python programs. In the process of studying, we will create our own library for the National Assembly, which you can use for experiments and further training. All code can be downloaded here . Having finished the book, or in the process of reading, you can choose one of the more complete libraries for the National Assembly, adapted for use in these projects.

The mathematical requirements for understanding the material are quite average. Most chapters have mathematical parts, but usually they are elementary algebra and function graphs. Sometimes I use more advanced math, but I structured the material so that you can understand it, even if some details elude you. Most of the math is used in chapter 2, which requires a bit of matanalysis and linear algebra. For those to whom they are not familiar, I begin Chapter 2 with an introduction to mathematics. If you find it difficult, just skip the chapter until the debriefing. In any case, do not worry about this.

A book is rarely at the same time oriented towards an understanding of principles and a practical approach. But I believe that it is better to study on the basis of the fundamental ideas of the National Assembly. We will write working code, and not just study abstract theory, and you can explore and extend this code. In this way, you will understand the basics, both theory and practice, and will be able to learn further.

Exercises and Tasks

Authors of technical books often warn the reader that he simply needs to complete all the exercises and solve all the problems. When reading such warnings to me, they always seem a little strange. Will something bad happen to me if I do not perform exercises and solve problems? Of course not. I will just save time by less deep understanding. Sometimes it's worth it. Sometimes not.

What is worth doing with this book? I advise you to try to complete most exercises, but do not try to solve most tasks.

Most of the exercises need to be completed because these are basic checks for a proper understanding of the material. If you cannot perform the exercise with relative ease, you must have missed something fundamental. Of course, if you are really stuck in some kind of exercise - drop it, maybe it's some kind of small misunderstanding, or maybe I have poorly formulated something. But if most of the exercises cause you difficulty, then you most likely need to reread the previous material.

Tasks are another matter. They are more difficult than exercises, and with some you will have a hard time. This is annoying, but of course patience in the face of such disappointment is the only way to truly understand and absorb the subject.

So I do not recommend solving all problems. Better yet - pick up your own project. You might want to use NS to classify your music collection. Or to predict the value of stocks. Or something else. But find an interesting project for you. And then you can ignore the tasks from the book, or use them purely as inspiration for working on your project. Problems with your own project will teach you more than working with any number of tasks. Emotional involvement is a key factor in mastery achievement.

Of course, while you may not have such a project. This is normal. Solve tasks for which you feel intrinsic motivation. Use material from the book to help you find ideas for personal creative projects.

Chapter 1

The human visual system is one of the wonders of the world. Consider the following sequence of handwritten numbers:



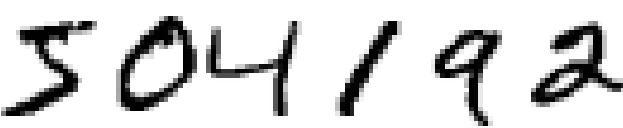
Most people read them easily, like 504192. But this simplicity is deceiving. In each hemisphere of the brain, a person has a primary visual cortex, also known as V1, which contains 140 million neurons and tens of billions of connections between them. At the same time, not only V1 is involved in human vision, but a whole sequence of brain regions - V2, V3, V4 and V5 - which are engaged in increasingly complex image processing. We carry in our heads a supercomputer tuned by evolution for hundreds of millions of years, and perfectly adapted to understand the visible world. Recognizing handwritten numbers is not so easy. It’s just that we people, amazingly, surprisingly well, recognize what our eyes show us. But almost all of this work is carried out unconsciously. And usually we don’t attach importance to what a difficult task our visual systems solve.

The difficulty of recognizing visual patterns becomes apparent when you try to write a computer program to recognize numbers like the ones above. What seems easy in our execution suddenly turns out to be extremely complex. The simple concept of how we recognize the forms - “the nine has a loop at the top and the vertical bar at the bottom right” - is not at all so simple for an algorithmic expression. By trying to articulate these rules clearly, you quickly get stuck in a quagmire of exceptions, pitfalls, and special occasions. The task seems hopeless.

NS approach to solving the problem in a different way. The idea is to take the many handwritten numbers known as teaching examples,



and develop a system that can learn from these examples. In other words, the National Assembly uses examples to automatically construct handwritten digit recognition rules. Moreover, by increasing the number of training examples, the network can learn more about handwritten numbers and improve its accuracy. So, although I have cited above just 100 case studies, perhaps we can create a better handwriting recognition system using thousands or even millions and billions of case studies.

In this chapter we will write a computer program that implements NS learning to recognize handwritten numbers. The program will be only 74 lines long, and will not use special libraries for the National Assembly. However, this short program will be able to recognize handwritten numbers with an accuracy of more than 96%, without requiring human intervention. Moreover, in future chapters we will develop ideas that can improve accuracy to 99% or more. In fact, the best commercial NSs do such a good job that they are used by banks to process checks, and the postal service to recognize addresses.

We concentrate on handwriting recognition, as this is a great prototype of a task for studying NS. Such a prototype is ideal for us: it is a difficult task (recognizing handwritten numbers is not an easy task), but not so complicated that it requires an extremely complex solution or immense computing power. Moreover, this is a great way to develop more complex techniques, such as GO. Therefore, in the book we will constantly return to the task of handwriting recognition. Later we will discuss how these ideas can be applied to other tasks of computer vision, to speech recognition, natural language processing and other areas.

Of course, if the purpose of this chapter was only to write a program for recognizing handwritten numbers, then the chapter would be much shorter! However, in the process we will develop many key ideas related to NS, including two important types of artificial neuron ( perceptron and sigmoid neuron), and the standard NS learning algorithm, stochastic gradient descent . In the text, I concentrate on explaining why everything is done this way, and on shaping your understanding of the National Assembly. This requires a longer conversation than if I just presented the basic mechanics of what is happening, but it costs a deeper understanding that you will have. Among other advantages - by the end of the chapter you will understand what a civil defense is and why it is so important.

Perceptrons

What is a neural network? To start, I’ll talk about one type of artificial neuron called the perceptron. Perceptrons were invented by the scientist Frank Rosenblatt in the 1950s and 60s , inspired by the early work of Warren McCallock and Walter Pitts . Today, other models of artificial neurons are used more often - in this book, and most modern works on NS mainly use the sigmoid model of the neuron. We will meet her soon. But to understand why sigmoid neurons are defined in this way, it is worth spending time analyzing the perceptron.

So how do perceptrons work? The perceptron receives several binary numbers x ₁ , x ₂ , ... and gives one binary number:



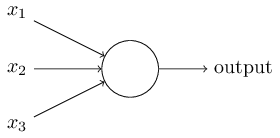
In this example, the perceptron has three input numbers, x ₁ , x ₂ , x ₃ . In general, there may be more or less of them. Rosenblatt proposed a simple rule for calculating the result. He introduced weights, w ₁ , w ₂ , real numbers, expressing the importance of the corresponding input numbers for the results. The output of a neuron, 0 or 1, is determined by whether a weighted sum is less or more than a certain threshold [threshold]$$. Like weights, the threshold is a real number, a parameter of a neuron. In mathematical terms:

$$

That's the whole description of the perceptron!

This is the basic mathematical model. A perceptron can be thought of as a decision maker by weighing evidence. Let me give you a not very realistic, but simple example. Let's say the weekend is coming, and you heard that a cheese festival will be held in your city. You like cheese, and try to decide whether to go to the festival or not. You can make a decision by weighing three factors:

1. Is the weather good?
2. Does your partner want to go with you?
3. Is the festival far from public transport? (You don’t have a car).

These three factors can be represented as binary variables x ₁ , x ₂ , x ₃ . For example, x ₁ = 1 if the weather is good, and 0 if it is bad. x ₂ = 1 if your partner wants to go, and 0 if not. Same for x ₃ .

Now, let's say you are so much fan of cheese that you are ready to go to the festival, even if your partner is not interested in it and it is difficult to get to it. But perhaps you just hate bad weather, and in case of bad weather you won’t go to the festival. You can use perceptrons to model such a decision making process. One way is to choose the weight w ₁ = 6 for the weather, and w ₂ = 2, w ₃= 2 for other conditions. A larger value of w ₁ means that the weather matters much more to you than whether your partner will join you or the proximity of the festival to a stop. Finally, suppose you select threshold 5 for the perceptron. With these options, the perceptron implements the desired decision model, giving 1 when the weather is good and 0 when it is bad. The desire of the partner and the proximity of the stop do not affect the output value.

By changing weights and thresholds, we can get different decision-making models. For example, let's say we take threshold 3. Then the perceptron decides that you need to go to the festival, either when the weather is nice, or when the festival is near a bus stop and your partner agrees to go with you. In other words, the model is different. Lowering the threshold means you want to go to the festival more.

Obviously, the perceptron is not a complete human decision making model! But this example shows how a perceptron can weigh different types of evidence to make decisions. It seems possible that a complex network of perceptrons can make very complex decisions:



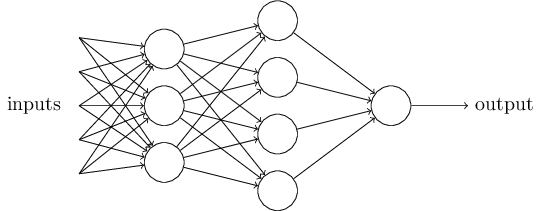
In this network, the first column of perceptrons - what we call the first layer of perceptrons - makes three very simple decisions, weighing the input evidence. What about perceptrons from the second layer? Each of them makes a decision, weighing the results of the first decision-making layer. In this way, the perceptron of the second layer can make a decision at a more complex and abstract level compared to the perceptron of the first layer. And even more complex decisions can be made by perceptrons on the third layer. In this way, a multilayer network of perceptrons can deal with complex decisions.

By the way, when I determined the perceptron, I said that it has only one output value. But in the network at the top, the perceptrons look like they have several output values. In fact, they have only one way out. Many output arrows are just a convenient way to show that the output of the perceptron is used as the input of several other perceptrons. This is less cumbersome than drawing a single branching exit.

Let's simplify the description of perceptrons. Condition$$clumsy, and we can agree on two changes to the record to simplify it. The first is to record$$ as a scalar product, $$, where w and x are vectors whose components are weights and input data, respectively. The second is to transfer the threshold to another part of the inequality, and replace it with a value known as perceptron displacement [bias],$$. Using displacement instead of a threshold, we can rewrite the perceptron rule:

$$

The offset can be represented as a measure of how easy it is to get a value of 1 at the output from the perceptron. Or, in biological terms, displacement is a measure of how easy it is to get the perceptron to activate. A perceptron with a very large bias is extremely easy to give 1. But with a very large negative bias, this is difficult to do. Obviously, the introduction of bias is a small change in the description of perceptrons, but later we will see that it leads to further simplification of the recording. Therefore, further we will not use the threshold, but will always use the offset.

I described perceptrons in terms of the method of weighing evidence for decision making. Another method of their use is the calculation of elementary logical functions, which we usually consider to be the main calculations, such as AND, OR and NAND. Suppose, for example, that we have a perceptron with two inputs, the weight of each of which is -2, and its offset is 3. Here it is:



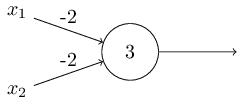
Input 00 gives output 1, because (−2) ∗ 0 + (- 2 ) ∗ 0 + 3 = 3 is greater than zero. The same calculations say that input 01 and 10 give 1. But 11 at the input gives 0 at the output, since (−2) ∗ 1 + (- 2) ∗ 1 + 3 = −1, less than zero. Therefore, our perceptron implements the NAND function!

This example shows that perceptrons can be used to compute basic logic functions. In fact, we can use perceptron networks to calculate any logical functions in general. The fact is that the NAND logic gate is universal for calculations - it is possible to build any calculations on its basis. For example, you can use NAND gates to create a circuit that adds two bits, x ₁ and x ₂ . To do this, calculate the bitwise sum$$, as well as the carry flag , which is 1 when both x ₁ and x ₂ are 1 - that is, the carry flag is simply the result of bitwise multiplication x ₁ x ₂ :



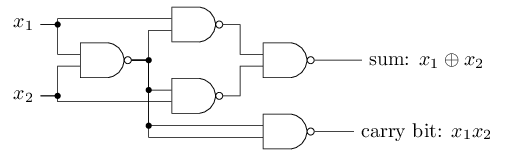
To get the equivalent network of perceptrons, we replace all NAND gates with perceptrons with two inputs, the weight of each of which is -2, and with an offset of 3. Here is the resulting network. Note that I moved the perceptron corresponding to the lower right valve, just to make it more convenient to draw arrows:



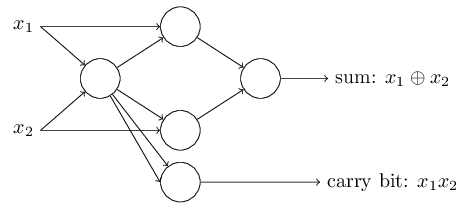
One noteworthy aspect of this perceptron network is that the output of the leftmost one is used twice as input to the bottom. Defining the model of the perceptron, I did not mention the admissibility of such a double exit scheme in the same place. In fact, it does not really matter. If we do not want to allow this, we can simply combine two lines with weights of -2 into one with a weight of -4. (If this does not seem obvious to you, stop and prove it to yourself). After this change, the network looks as follows, with all unallocated weights equal to -2, all offsets equal to 3, and one weight -4 is marked:



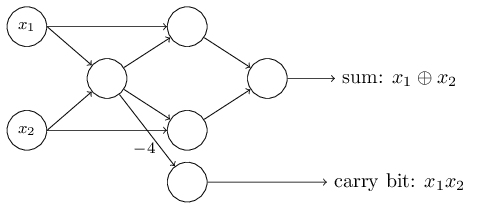
Such a record of perceptrons that have an output but no inputs:



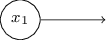
is just an abbreviation. This does not mean that he has no inputs. To understand this, suppose we have a perceptron without inputs. Then the weighted sum ∑ _j w _j x _j would always be zero, so the perceptron would give 1 for b> 0 and 0 for b ≤ 0. That is, the perceptron would just give a fixed value, and not what we need (x ₁ in the example higher). It is better to consider the input perceptrons not as perceptrons, but as special units that are simply defined so as to produce the desired values ​​x ₁ , x ₂ , ...

The adder example demonstrates how a perceptron network can be used to simulate a circuit containing many NAND gates. And since these gates are universal for calculations, therefore, perceptrons are universal for calculations.

The computational versatility of perceptrons is both encouraging and disappointing. It is encouraging, ensuring that the perceptron network can be as powerful as any other computing device. Disappointing, giving the impression that perceptrons are just a new type of NAND logic gate. So-so discovery!

However, the situation is actually better. It turns out that we can develop training algorithms that can automatically adjust the weights and displacements of the network from artificial neurons. This adjustment takes place in response to external stimuli, without the direct intervention of a programmer. These learning algorithms allow us to use artificial neurons in a way radically different from ordinary logic gates. Instead of explicitly registering a circuit from NAND gates and others, our neural networks can simply learn how to solve problems, sometimes those for which it would be extremely difficult to directly design a regular circuit.

Sigmoid neurons

Learning algorithms are great. However, how to develop such an algorithm for a neural network? Suppose we have a network of perceptrons that we want to use to train us in solving a problem. Suppose the input to the network may be pixels of a scanned image of a handwritten digit. And we want the network to know the weights and offsets needed to correctly classify the numbers. To understand how such training can work, let’s imagine that we are slightly changing a certain weight (or bias) in the network. We want this small change to lead to a small change in the network output. As we will soon see, this property makes learning possible. Schematically, we want the following (obviously, such a network is too simple to recognize handwriting!):



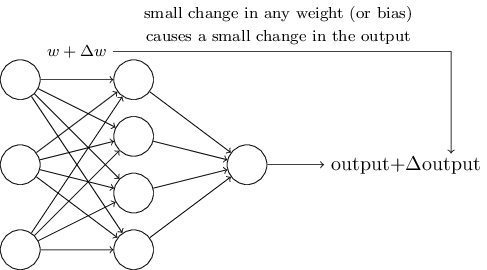
If a small change in weight (or bias) would lead to a small change in the output result, we could change the weights and biases so that our network behaves a little closer to what we want. For example, let's say that the network incorrectly assigned the image to “8”, although it should have been to “9”. We could figure out how to make a small change in weight and displacement so that the network gets a little closer to classifying the image as “9”. And then we would repeat this, changing weights and shifts again and again to get the best and best result. The network would learn.

The problem is that if there are perceptrons in the network, this does not happen. A small change in the weights or displacement of any perceptron can sometimes lead to a change in its output to the opposite, say, from 0 to 1. Such a flip can change the behavior of the rest of the network in a very complicated way. And even if now our “9” is correctly recognized, the behavior of the network with all the other images has probably completely changed in a way that is difficult to control. Because of this, it is difficult to imagine how we can gradually adjust weights and offsets so that the network gradually approaches the desired behavior. Perhaps there is some clever way around this problem. But there is no simple solution to the problem of learning a network of perceptrons.

This problem can be circumvented by introducing a new type of artificial neuron called sigmoid neuron. They are similar to perceptrons, but modified so that small changes in weights and offsets result in only small changes in the output. This is a basic fact that will allow the network of sigmoid neurons to learn.

Let me describe a sigmoid neuron. We will draw them in the same way as perceptrons:



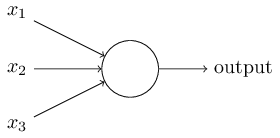
It has the same input data x ₁ , x ₂ , ... But instead of being equal to 0 or 1, these inputs can have any value in the range from 0 to 1. K for example, a value of 0.638 would be a valid input value for a sigmoid neuron (SN). Just like the perceptron, SN has weights for each input, w ₁ , w ₂, ... and total bias b. But its output value will not be 0 or 1. It will be σ (w⋅x + b), where σ is the sigmoid.

By the way, σ is sometimes called a logistic function , and this class of neurons is called logistic neurons. It is useful to remember this terminology, since these terms are used by many people working with neural networks. However, we will adhere to sigmoid terminology.

The function is defined as follows:

$$

In our case, the output value of the sigmoid neuron with input data x ₁ , x ₂ , ... by weights w ₁ , w ₂ , ... and offset b will be considered as:

$$

At first glance, CH seem completely unlike neurons. The algebraic look of a sigmoid may seem confusing and obscure if you are not familiar with it. In fact, there are many similarities between perceptrons and SN, and the algebraic form of a sigmoid turns out to be more a technical detail than a serious barrier to understanding.

To understand the similarities to the perceptron model, suppose that z ≡ w ⋅ x + b is a large positive number. Then e - z ≈ 0, therefore, σ (z) ≈ 1. In other words, when z = w ⋅ x + b is large and positive, the SN yield is approximately 1, as in the perceptron. Suppose that z = w ⋅ x + b is large with a minus sign. Then e - z → ∞, and σ (z) ≈ 0. So for large z with a minus sign, the behavior of the SN also approaches the perceptron. And only when w ⋅ x + b has an average size, are serious deviations from the perceptron model observed.

What about the algebraic form of σ? How do we understand him? In fact, the exact form of σ is not so important - the shape of the function on the graph is important. Here it is:



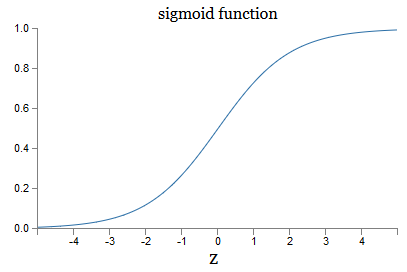
This is a smooth version of a step function:



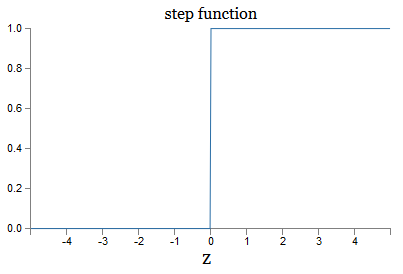
If σ were stepwise, then the SN would be a perceptron, since it would have 0 or 1 output depending on the sign w ⋅ x + b (well, in fact, at z = 0, the perceptron gives 0, and the step function 1 , so at that point, the function would have to be changed).

Using the real function σ, we get a smoothed perceptron. And the main thing here is the smoothness of the function, not its exact form. Smoothness means that small changes Δw _j weights and δb offsets will give small changes Δoutput of the output. Algebra tells us that Δoutput is well approximated as follows:

$$

Where the summation is over all weights w _j , and ∂output / ∂w _j and ∂output / ∂b denote the partial derivatives of the output with respect to w _j and b, respectively. Do not panic if you feel insecure in the company of private derivatives! Although the formula looks complicated, with all these partial derivatives, it actually says something quite simple (and useful): Δoutput is a linear function depending on the Δw _j and Δb weights and biases. Its linearity makes it easy to select small changes in weights and offsets to achieve any desired small output bias. So, although SNs are similar to perceptrons in qualitative behavior, they make it easier to understand how the output can be changed by changing weights and displacements.

If the general form σ is important for us, and not its exact form, then why do we use such a formula (3)? In fact, later we will sometimes consider neurons whose output is f (w ⋅ x + b), where f () is some other activation function. The main thing that changes when the function changes is the value of the partial derivatives in equation (5). It turns out that when we then calculate these partial derivatives, the use of σ greatly simplifies algebra, since exponents have very nice properties when differentiating. In any case, σ is often used in working with neural networks, and most often in this book we will use such an activation function.

How to interpret the result of the work of CH? Obviously, the main difference between the perceptrons and the CH is that the CH does not give out only 0 or 1. Their output can be any real number from 0 to 1, so values ​​like 0.173 or 0.689 are valid. This can be useful, for example, if you want the output value to indicate, for example, the average brightness of the pixels of the image received at the input of the NS. But sometimes it can be inconvenient. Suppose we want the network output to say that “image 9 was input” or “input image not 9”. Obviously, it would be easier if the output values ​​were 0 or 1, like a perceptron. But in practice, we can agree that any output value of at least 0.5 would mean “9” at the input, and any value less than 0.5 would mean that it is “not 9”.

Exercises

• CH simulating perceptrons, part 1

Suppose we take all the weights and offsets from a network of perceptrons, and multiply them by a positive constant c> 0. Show that the network behavior does not change.

• CH simulating perceptrons, part 2

Suppose we have the same situation as in the previous problem - a network of perceptrons. Also suppose that the input data for the network is selected. We do not need a specific value, the main thing is that it is fixed. Suppose the weights and displacements are such that w⋅x + b ≠ 0, where x is the input value of any perceptron of the network. Now we replace all the perceptrons in the network with SN, and multiply the weights and displacements by the positive constant c> 0. Show that in the limit c → ∞ the behavior of the network from the SN will be exactly the same as the networks of perceptrons. How will this statement be violated if for one of the perceptrons w⋅x + b = 0?

Neural network architecture

In the next section, I will introduce a neural network capable of a good classification of handwritten numbers. Before that, it’s useful to explain the terminology that allows us to point to different parts of the network. Let's say we have the following network:



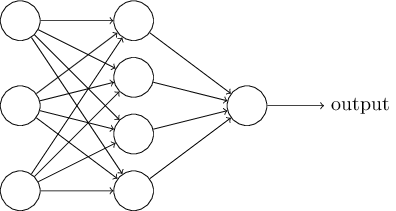
As I mentioned, the leftmost layer in the network is called the input layer, and its neurons are called input neurons. The rightmost, or output layer, contains output neurons, or, as in our case, one output neuron. The middle layer is called hidden, because its neurons are neither input nor output. The term "hidden" may sound a little mysterious - when I first heard it, I decided that it should have some deep philosophical or mathematical importance - however, it only means "neither entrance nor exit." The network above has only one hidden layer, but some networks have several hidden layers. For example, in the following four-layer network there are two hidden layers:



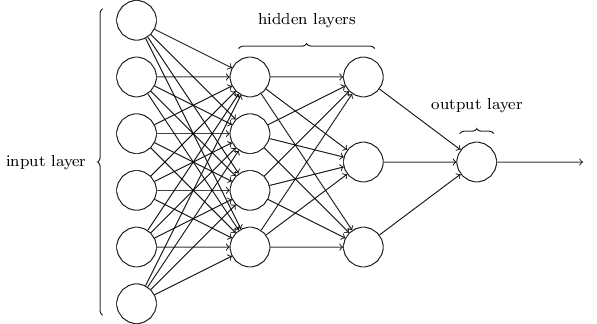
This may be confusing, but for historical reasons, such multi-layer networks are sometimes called multilayer perceptrons, MLPs, although they consist of sigmoid neurons rather than perceptrons. I am not going to use such terminology because it is confusing, but I must warn about its existence.

Designing input and output layers is sometimes a simple task. For example, let's say we are trying to determine whether the handwritten number means "9" or not. A natural network circuit will encode the brightness of the image pixels in the input neurons. If the image is black and white, 64x64 pixels in size, then we will have 64x64 = 4096 input neurons, with brightness in the range from 0 to 1. The output layer will contain only one neuron, whose value less than 0.5 will mean that "on the input was not 9 ", but values ​​more will mean that" the input was 9 ".

And while designing input and output layers is often a simple task, designing hidden layers can be a difficult art. In particular, it is not possible to describe the process of developing hidden layers with a few simple rules of thumb. Researchers of the National Assembly have developed many heuristic rules for the design of hidden layers that help to obtain the desired behavior of neural networks. For example, such a heuristic can be used to understand how to achieve a compromise between the number of hidden layers and the time available for training the network. Later we will encounter some of these rules.

So far, we have been discussing NSs in which the output of one layer is used as input for the next. Such networks are called direct distribution neural networks. This means that there are no loops in the network - information always goes forward, and never feeds back. If we had loops, we would encounter situations in which the input sigmoid would depend on the output. It would be hard to comprehend, and we do not allow such loops.

However, there are other models of artificial NSs in which it is possible to use feedback loops. These models are called recurrent neural networks.(RNS). The idea of ​​these networks is that their neurons are activated for limited periods of time. This activation can stimulate other neutrons, which can be activated a bit later, also for a limited time. This leads to the activation of the following neurons, and over time we get a cascade of activated neurons. Loops in such models do not present problems, since the output of a neuron affects its entry at a later time, and not immediately.

RNSs were not as influential as NSs of direct distribution, in particular because training algorithms for RNSs so far have less potential. However, the RNS still remains extremely interesting. In the spirit of work, they are much closer to the brain than NS of direct distribution. It is possible that the RNS will be able to solve important problems that, with the help of direct distribution NS, can be solved with great difficulties. However, in order to limit the scope of our study, we will concentrate on the more widely used NS of direct distribution.

Simple ink classification network

Having defined the neural networks, we will return to handwriting recognition. The task of recognizing handwritten numbers can be divided into two subtasks. First, we want to find a way to split an image containing many digits into a sequence of individual images, each of which contains one digit. For example, we would like to split the image



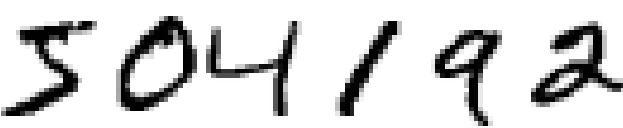
into six separate



We humans easily solve this segmentation problem, but it is difficult for a computer program to correctly split the image. After segmentation, the program needs to classify each individual digit. So, for example, we want our program to recognize that the first digit



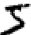
is 5.

We will concentrate on creating a program for solving the second problem, the classification of individual numbers. It turns out that the problem of segmentation is not so difficult to solve as soon as we find a good way to classify individual digits. There are many approaches to solving the segmentation problem. One of them is to try many different ways of image segmentation using the classifier of individual digits, evaluating each attempt. Trial segmentation is highly appreciated if the classifier of individual digits is confident in the classification of all segments, and low if it has problems in one or more segments. The idea is that if the classifier has problems somewhere, this most likely means that the segmentation is incorrect. This idea and other options can be used for a good solution to the segmentation problem. So instead of

To recognize individual digits, we will use NS from three layers:



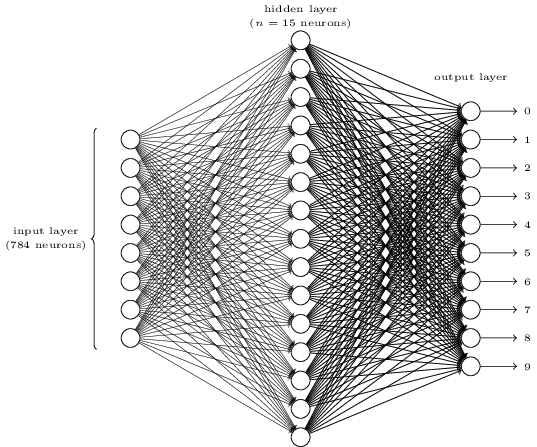
The input network layer contains neurons encoding different values ​​of the input pixels. As will be indicated in the next section, our training data will consist of many images of scanned handwritten digits of 28x28 pixels in size, so the input layer contains 28x28 = 784 neurons. For simplicity, I did not indicate most of the 784 neurons in the diagram. Incoming pixels are black and white, with a value of 0.0 indicating white, 1.0 indicating black, and intermediate values ​​indicating increasingly darker shades of gray.

The second layer of the network is hidden. We denote the number of neurons in this layer n, and we will experiment with different values ​​of n. The above example shows a small hidden layer containing only n = 15 neurons.

There are 10 neurons in the output layer of the network. If the first neuron is activated, that is, its output value is ≈ 1, this indicates that the network considers that the input was 0. If the second neuron is activated, the network believes that the input was 1. And so on. Strictly speaking, we number the output neurons from 0 to 9, and look at which of them had the maximum activation value. If this is, say, neuron No. 6, then our network believes that the input was number 6. And so on.

You may wonder why we need to use ten neurons. After all, we want to know which digit from 0 to 9 corresponds to the input image. It would be natural to use only 4 output neurons, each of which would take a binary value, depending on whether its output value is closer to 0 or 1. Four neurons would be enough, since 2⁴ = 16, more than 10 possible values. Why should our network use 10 neurons? Is this ineffective? The basis for this is empirical; we can try both variants of the network, and it turns out that for this task, a network with 10 output neurons is better trained to recognize numbers than a network with 4. However, the question remains, why are 10 output neurons better. Is there any heuristic that would tell us in advance that 10 output neurons should be used instead of 4?

To understand why, it is useful to think about what a neural network does. First, consider the option with 10 output neurons. We focus on the first output neuron, which is trying to decide whether the incoming image is zero. He does this by weighing evidence obtained from a hidden layer. What do hidden neurons do? Suppose the first neuron in the hidden layer determines whether there is something like this in the picture:



He can do this by assigning large weights to the pixels matching this image, and small weights to the rest. Likewise, suppose that the second, third and fourth neurons in the hidden layer are looking for whether there are similar fragments in the image:



As you might have guessed, together these four fragments give the image 0, which we saw earlier:



So, if the four hidden neurons are activated, we can conclude that the number is 0. Of course, this is not the only evidence that 0 was displayed there - we can get 0 in many other ways (by slightly shifting these images or slightly distorting them). However, we can say for sure that, at least in this case, we can conclude that there was 0 at the input.

If we assume that the network works like this, we can give a plausible explanation of why it is better to use 10 output neurons instead of 4. If we had 4 output neurons, then the first neuron would try to decide what is the most significant bit of the incoming digit. And there is no easy way to associate the most significant bit with the simple forms given above. It’s hard to imagine any historical reasons why parts of the form of a digit would be somehow related to the most significant bit of the output.

However, all of the above is supported only by heuristics. Nothing speaks in favor of the fact that a three-layer network should work as I said, and hidden neurons should find simple components of forms. Perhaps the tricky learning algorithm will find some weights that will allow us to use only 4 output neurons. However, as a heuristic, my method works well, and can save you considerable time in developing a good NS architecture.

Exercises

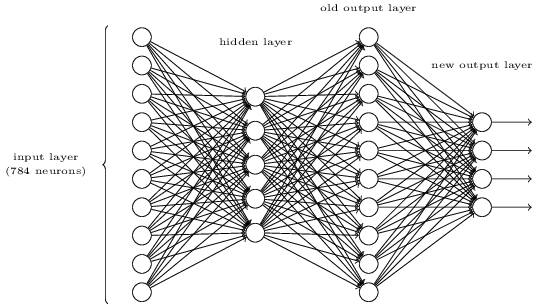
• Существует способ определить побитовое представление числа, добавив дополнительный слой к трёхслойной сети. Дополнительный слой преобразует выходные значения предыдущего слоя в двоичный формат, как показано на рисунке ниже. Найдите наборы весов и смещений для нового выходного слоя. Предполагаем, что первые 3 слоя нейронов таковы, что правильный выход с третьего слоя (бывший выходной слой) активируется значениями не менее 0,99, а неправильные выходные значения не превышают 0,01.

Обучение с градиентным спуском

So, we have the NA scheme - how to learn to recognize numbers? The first thing we need is training data, the so-called training data set. We will use the MNIST kit containing tens of thousands of scanned images of handwritten numbers, and their correct classification. The name MNIST received due to the fact that it is a modified subset of the two data sets collected by NIST , the US National Institute of Standards and Technology. Here are some images from MNIST:



These are the same numbers that were given at the beginning of the chapter as a recognition task. Of course, when checking the NS, we will ask her to recognize the wrong images that were already in the training set!

MNIST data consists of two parts. The first contains 60,000 images intended for training. These are scanned manuscripts of 250 people, half of whom were employees of the US Census Bureau, and the other half were high school students. Images are black and white, measuring 28x28 pixels. The second part of the MNIST dataset is 10,000 images to test the network. This is also a black and white image 28x28 pixels. We will use this data to evaluate how well the network has learned to recognize numbers. To improve the quality of the assessment, these figures were taken from another 250 people who did not participate in the recording of the training set (although these were also Bureau employees and high school students). This helps us to make sure that our system can recognize the handwriting of people that it did not meet during training.

The training input will be denoted by x. It will be convenient to treat each input image x as a vector with 28x28 = 784 measurements. Each value inside the vector indicates the brightness of one pixel in the image. We will denote the output value as y = y (x), where y is a ten-dimensional vector. For example, if a certain training image x contains 6, then y (x) = (0,0,0,0,0,0,1,0,0,0) ^T will be the vector we need. T is a transpose operation that turns a row vector into a column vector.

We want to find an algorithm that allows us to look for such weights and offsets so that the network output approaches y (x) for all training input x. To quantify the approximation of this goal, we define a cost function (sometimes called a loss function; in the book we will use the cost function, but keep in mind another name):

$$

Here w denotes a set of network weights, b is a set of offsets, n is the number of training input data, a is the vector of output data when x is input data, and the sum passes through all training input x. The output, of course, depends on x, w and b, but for simplicity I did not designate this dependence. The notation || v || means the length of the vector v. We will call C a quadratic cost function; sometimes it is also called the standard error, or MSE. If you look closely at C, you can see that it is not negative, since all members of the sum are non-negative. In addition, the cost of C (w, b) becomes small, that is, C (w, b) ≈ 0, precisely when y (x) is approximately equal to the output vector a for all training input data x. So our algorithm worked well if we managed to find weights and offsets such that C (w, b) ≈ 0. And vice versa, it worked poorly when C (w, b) large - this means that y (x) does not match the output for a large amount of input. It turns out that the goal of the training algorithm is to minimize the cost of C (w, b) as a function of weights and offsets. In other words, we need to find a set of weights and offsets that minimize the value of cost. We will do this using an algorithm called gradient descent.

Why do we need a quadratic value? Aren't we mainly interested in the number of images correctly recognized by the network? Is it possible to simply maximize this number directly, and not minimize the intermediate value of the quadratic value? The problem is that the number of correctly recognized images is not a smooth function of the weights and offsets of the network. For the most part, small changes in weights and offsets will not change the number of correctly recognized images. Because of this, it is hard to understand how to change weights and biases to improve efficiency. If we use a smooth cost function, it will be easy for us to understand how to make small changes in weights and offsets in order to improve the cost. Therefore, we will first focus on the quadratic value, and then we will study the accuracy of the classification.

Even considering that we want to use a smooth cost function, you may still be interested in why we chose the quadratic function for equation (6)? Is it not possible to choose it arbitrarily? Perhaps if we chose a different function, we would get a completely different set of minimizing weights and offsets? A reasonable question, and later we will again examine the cost function and make some corrections to it. However, the quadratic cost function works great for understanding the basic things in learning NS, so for now we will stick to it.

To summarize: our goal in training NS is to find weights and offsets that minimize the quadratic cost function C (w, b). The task is well posed, but so far it has many distracting structures - the interpretation of w and b as weights and offsets, the function σ hidden in the background, the choice of network architecture, MNIST, and so on. It turns out that we can understand a lot, ignoring most of this structure, and concentrating only on the aspect of minimization. So for now, we will forget about the special form of the cost function, communication with the National Assembly, and so on. Instead, we are going to imagine that we just have a function with many variables, and we want to minimize it. We will develop a technology called gradient descent, which can be used to solve such problems. And then we come back to a certain function,

Well, let's say we are trying to minimize some function C (v). It can be any function with real values ​​of many variables v = v ₁ , v ₂ , ... Note that I replaced the notation w and b with v to show that it can be any function - we are no longer obsessed with HC. It is useful to imagine that a function C has only two variables - v ₁ and v ₂ :



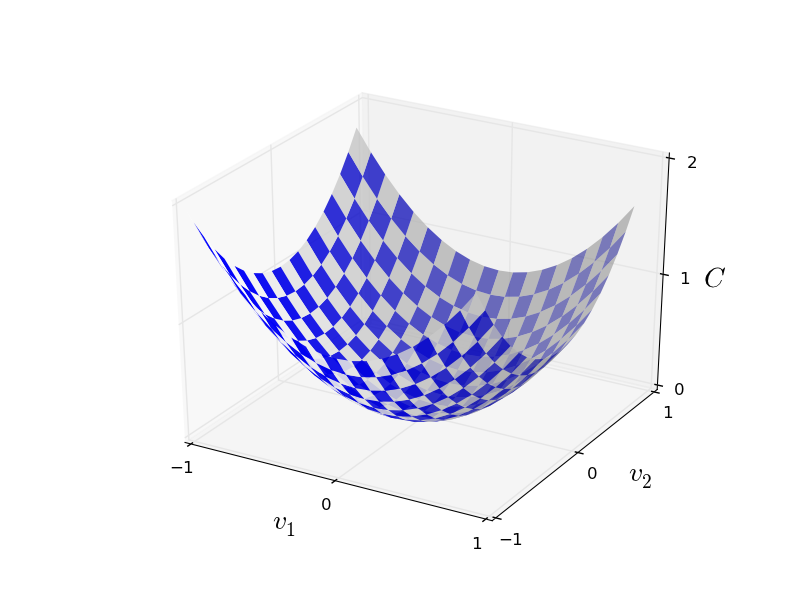
We would like to find where C reaches a global minimum. Of course, with the function drawn above, we can study the graph and find the minimum. In this sense, I may have given you a too simple function! In the general case, C can be a complex function of many variables, and it is usually impossible to just look at the graph and find the minimum.

One way to solve the problem is to use algebra to find the minimum analytically. We can calculate the derivatives and try to use them to find the extremum. If we are lucky, this will work when C is a function of one or two variables. But with a large number of variables, this turns into a nightmare. And for NSs, we often need much more variables - for the largest NSs, the cost functions in a complex way depend on billions of weights and displacements. Using algebra to minimize these functions will fail!

(Having stated that it would be more convenient for us to consider C as a function of two variables, I said twice in two paragraphs “yes, but what if it is a function of a much larger number of variables?” I apologize. Believe us that it will really be useful to represent C as a function two variables, it’s just that sometimes this picture falls apart, which is why the previous two paragraphs were needed. zya.)

Okay, that means algebra won't work. Fortunately, there is a great analogy that offers a well-functioning algorithm. We imagine our function as something like a valley. With the latest schedule, it will not be so difficult to do. And we imagine a ball rolling along the slope of the valley. Our experience tells us that the ball will eventually slide to the very bottom. Perhaps we can use this idea to find the minimum of a function? We randomly select the starting point for an imaginary ball, and then simulate the movement of the ball, as if it was rolling to the bottom of the valley. We can use this simulation simply by counting the derivatives (and, possibly, the second derivatives) of C - they will tell us everything about the local shape of the valley, and therefore about how our ball will roll.

Based on what you wrote, you might think that we will write down Newton’s equations of motion for the ball, consider the effects of friction and gravity, and so on. In fact, we will not be so close to following this analogy with the ball - we are developing an algorithm for minimizing C, and not an exact simulation of the laws of physics! This analogy should stimulate our imagination, and not limit our thinking. So instead of diving into the complex details of physics, let's ask a question: if we were appointed god for one day, and we would create our own laws of physics, telling the ball how to roll which law or the laws of motion we would choose, so that the ball always rolls onto bottom of the valley?

To clarify the issue, we’ll think about what happens if we move the ball a small distance Δv ₁ in the direction of v ₁, and a small distance Δv ₂ in the direction of v ₂ . Algebra tells us that C changes as follows:

$$

We will find a way to choose such Δv ₁ and Δv ₂ so that ΔC is less than zero; that is, we will select them so that the ball rolls down. To understand how to do this, it is useful to define Δv as the vector of changes, that is, Δv ≡ (Δv ₁ , Δv ₂ ) ^T , where T is the transpose operation that turns row vectors into column vectors. We also define the gradient vector C as partial derivatives (∂S / ∂v ₁ , ∂S / ∂v ₂ ) ^T . We denote the gradient vector by ∇С:

$$

Soon we will rewrite the change in ΔC through Δv and the gradient ∇C. In the meantime, I want to clarify something, because of which people often hang on the gradient. When they first met with ∇C, people sometimes do not understand how they should perceive the symbol ∇. What does it specifically mean? In fact, you can safely consider ∇C a single mathematical object - a previously defined vector - which is simply written using two characters. From this point of view, ∇ is like waving a flag informing that "∇C is a gradient vector." There are more advanced points of view from which ∇ can be regarded as an independent mathematical entity (for example, as a differentiation operator), but we do not need them.

With such definitions, expression (7) can be rewritten as:

$$

This equation helps explain why ∇C is called a gradient vector: it connects changes in v with changes in C, just as expected from an entity called gradient. [eng. gradient - deviation / approx. transl.] However, it is more interesting that this equation allows us to see how to choose Δv so that ΔC is negative. Let's say we choose

$$

where η is a small positive parameter (learning speed). Then equation (9) tells us that ΔC ≈ - η ∇C ⋅ ∇C = - η || ∇C || ² . Since || ∇C || ² ≥ 0, this ensures that ΔC ≤ 0, that is, C will decrease all the time if we change v, as prescribed in (10) (of course, as part of the approximation from equation (9)). And this is exactly what we need! Therefore, we take equation (10) to determine the "law of motion" of the ball in our gradient descent algorithm. That is, we will use equation (10) to calculate the Δv value, and then we will move the ball to this value:

$$

Then we again apply this rule for the next move. Continuing the repetition, we will lower C until, hopefully, we reach a global minimum.

Summing up, gradient descent works through sequential calculation of the gradient ∇ C, and subsequent displacement in the opposite direction, which leads to a “fall” along the slope of the valley. This can be visualized as follows:



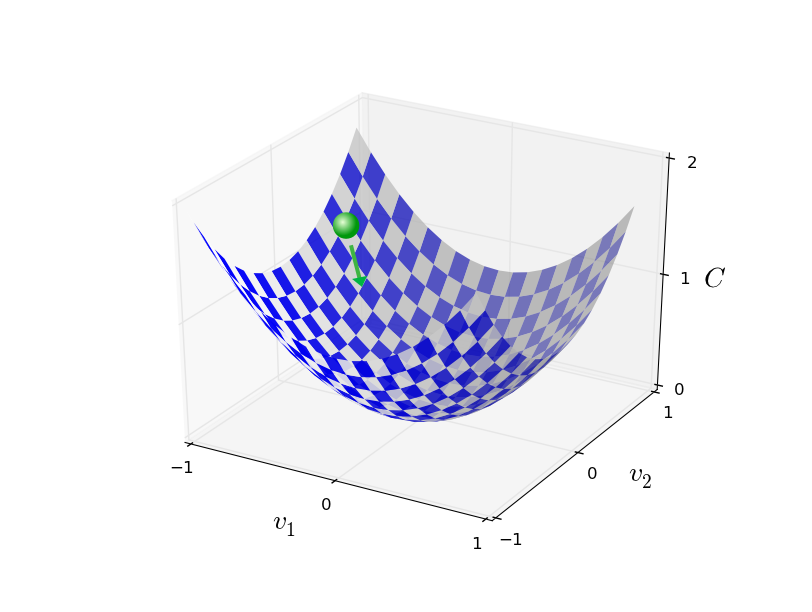
Note that with this rule, gradient descent does not reproduce real physical motion. In real life, the ball has an impulse that can allow it to roll across the slope, or even roll up for some time. Only after the work of the friction force is the ball guaranteed to roll down the valley. Our selection rule Δv just says “go down”. A pretty good rule to find the minimum!

For gradient descent to work correctly, we need to choose a sufficiently small value of the learning speed η so that equation (9) is a good approximation. Otherwise, it may turn out that ΔC> 0 - nothing good! At the same time, it is not necessary that η be too small, since then the changes in Δv will be tiny, and the algorithm will work too slowly. In practice, η changes so that equation (9) gives a good approximation, and the algorithm does not work too slowly. Later we will see how it works.

I explained gradient descent when function C depended on only two variables. But everything works the same way if C is a function of many variables. Suppose she has m variables, v ₁ , ..., v _m. Then the change in ΔC caused by a small change in Δv = (Δv ₁ , ..., Δv _m ) ^T will be

$$

where the gradient ∇C is the vector

$$

As with two variables, we can choose

$$

and ensure that our approximate expression (12) for ΔC is negative. This gives us a way to go along the gradient to a minimum, even when C is a function of many variables, applying the update rule over and over again.

$$

This update rule can be considered the defining gradient descent algorithm. It gives us a method of repeatedly changing the position of v in search of the minimum of the function C. This rule does not always work - several things may go wrong, preventing the gradient descent from finding the global minimum of C - we will return to this point in the following chapters. But in practice, gradient descent often works very well, and we will see that in the National Assembly this is an effective way to minimize the cost function, and therefore, train the network.

In a sense, gradient descent can be considered the optimal minimum search strategy. Suppose we are trying to move Δv to a position to minimize C. This is equivalent to minimizing ΔC ≈ ∇C ⋅ Δv. We will limit the step size so that || Δv || = ε for some small constant ε> 0. In other words, we want to move a small distance of a fixed size, and try to find the direction of movement that decreases C as much as possible. It can be proved that the choice of Δv minimizing ∇C ⋅ Δv is Δv = -η∇C, where η = ε / || ∇C || is determined by the restriction || Δv || = ε. So gradient descent can be considered a way to take small steps in the direction that decreases C. most.

Exercises

• Докажите утверждение из последнего параграфа. Подсказка: если вы не знакомы с неравенством Коши — Буняковского, возможно, вам поможет, если вы узнаете о нём побольше.
• Я объяснял про градиентный спуск, когда С является функцией двух переменных, и когда она является функцией многих переменных. Что будет, если С будет функцией всего одной переменной? Можете ли вы дать геометрическую интерпретацию работы градиентного спуска в одномерном случае?

People have studied many options for gradient descent, including those that more accurately reproduce a real physical ball. Such options have their advantages, but also a big drawback: the need to calculate the second partial derivatives of C, which can consume a lot of resources. To understand this, suppose that we need to calculate all the second partial derivatives ∂ ² C / ∂v _j ∂v _k . If the variables v _{j are} million, then we need to calculate about a trillion (a million squared) of the second partial derivatives (actually, half a trillion, since ∂ ² C / ∂v _j ∂v _k = ∂ ² C / ∂v _k ∂v _j. But you caught the essence). This will require a lot of computing resources. There are tricks to avoid this, and the search for alternatives to gradient descent is an area of ​​active research. However, in this book we will use gradient descent and its variants as the main approach to learning NS.

How do we apply gradient descent to NA learning? We need to use it to search for weights w _k and offsets b _l that minimize the cost equation (6). Let's rewrite the gradient descent update rule by replacing the v _j variables with weights and offsets. In other words, now our “position” has the components w _k and b _l , and the gradient vector ∇C has the corresponding components ∂C / ∂w_k and ∂C / ∂b _l . Having written our update rule with new components, we get:

$$

$$

By reapplying this update rule, we can “roll downhill” and, with any luck, find the minimum cost function. In other words, this rule can be used to train the National Assembly.

There are several obstacles to applying the gradient descent rule. We will study them in more detail in the following chapters. But for now, I want to mention only one problem. To understand it, let's go back to the quadratic value in equation (6). Note that this cost function looks like C = 1 / n ∑ _x C _x , that is, it is the average cost C _x ≡ (|| y (x) −a || ² ) / 2 for individual training examples. In practice, to calculate the gradient ∇C we need to calculate the gradients ∇C _xseparately for each training input x, and then average them, ∇C = 1 / n ∑ _x ∇C _x . Unfortunately, when the amount of input will be very large, it will take a very long time, and such training will be slow.

To speed up learning, you can use stochastic gradient descent. The idea is to approximately calculate the ∇C gradient by calculating ∇C _x for a small random sample of training input. By calculating their average, we can quickly get a good estimate of the true gradient ∇C, and this helps to accelerate the gradient descent, and therefore training.

Formulating more precisely, stochastic gradient descent works through random sampling of a small number of m training input data. We will call this random data X ₁ , X ₂ , .., X _m , and call it a mini-packet. If the sample size m is large enough, the average value of ∇C _{X j} will be close enough to the average of all ∇Cx, i.e.

$$

where the second amount goes over the entire set of training data. By interchanging parts, we get

$$

which confirms that we can estimate the overall gradient by calculating the gradients for a randomly selected minipack.

To relate this directly to the training of NS, let us assume that w _k and b _l denote the weights and displacements of our NS. Then the stochastic gradient descent selects a random mini-packet of input data, and learns from them

$$

$$

where is the summation over all training examples X _j in the current mini-package. Then we select another random mini-package and study on it. And so on, until we exhaust all the training data, which is called the end of the training era. At this moment, we are starting anew a new era of learning.

By the way, it is worth noting that the agreements regarding the scaling of the cost function and updating the weights and offsets differ in a mini-package. In equation (6), we scaled the cost function 1 / n times. Sometimes people omit 1 / n by adding up the costs of individual training examples, instead of calculating the average. This is useful when the total number of training examples is not known in advance. This can happen, for example, when additional data appears in real time. In the same way, mini-package update rules (20) and (21) sometimes omit the 1 / m member in front of the sum. Conceptually, this does not affect anything, since it is equivalent to a change in the learning speed η. However, it is worth paying attention to when comparing various works.

A stochastic gradient descent can be thought of as a political vote: it is much easier to take a sample in the form of a mini-package than to apply a gradient descent to a full sample - just like a poll at the exit from a site is easier than conducting a full-fledged election. For example, if our training set has a size of n = 60,000, like MNIST, and we make a sample of a mini-package of size m = 10, then we will speed up the gradient estimation by 6000 times! Of course, the estimate will not be ideal — there will be statistical fluctuation in it — but it does not need to be ideal: we only need to move in the direction that decreases C, which means that we do not need to calculate the gradient accurately. In practice, stochastic gradient descent is a common and powerful teaching technique for the National Assembly, and the base of most of the teaching technologies that we will develop as part of the book.

Упражнения

• Экстремальная версия градиентного спуска использует размер мини-пакета равный 1. То есть, при входных данных x мы обновляем наши веса и смещения по правилам w_k → w′_k = w_k − η ∂C_x / ∂w_k и b_l → b′_l = b_l − η ∂C_x / ∂b_l. Затем мы выбираем другой пример обучающих входных данных и снова обновляем веса и смещения. И так далее. Эта процедура известна, как онлайн-, или инкрементальное обучение. В онлайн-обучении НС учиться на основе одного обучающего экземпляра входных данных за раз (как люди). Назовите одно преимущество и один недостаток онлайн-обучения по сравнению со стохастическим градиентным спуском с размером мини-пакета в 20.

Let me end this section with a discussion of a topic that sometimes bothers people who have first encountered a gradient descent. In NS, the value of C is a function of many variables - all weights and offsets - and in a sense, determines the surface in a very multidimensional space. People begin to think: "I will have to visualize all these additional dimensions." And they begin to worry: “I can’t navigate in four dimensions, not to mention five (or five millions).” Do they have some special quality that the “real” supermathematics have? Of course not. Even professional mathematicians cannot visualize four-dimensional space quite well - if at all. They go to tricks, developing other ways of representing what is happening. This is exactly what we did: we used the algebraic (rather than visual) representation of ΔC to understand how to move so that C decreases. People who do a good job with a large number of dimensions have in their minds a large library of similar techniques; our algebraic trick is just one example. These techniques may not be as simple as we are accustomed to when visualizing three dimensions, but when you create a library of similar techniques, you begin to think well in higher dimensions. I will not go into details, but if you are interested, you may like what are we used to when visualizing three dimensions, but when you created a library of similar techniques, you begin to think well in higher dimensions. I will not go into details, but if you are interested, you may like what are we used to when visualizing three dimensions, but when you created a library of similar techniques, you begin to think well in higher dimensions. I will not go into details, but if you are interested, you may likeA discussion of some of these techniques by professional mathematicians who are used to thinking in higher dimensions. Although some of the techniques discussed are quite complex, most of the best answers are intuitive and accessible to everyone.

Implementing a network for classifying numbers

Ok, now let's write a program that learns to recognize handwritten digits using stochastic gradient descent and training data from MNIST. We will do this with a short program in python 2.7 consisting of only 74 lines! The first thing we need is to download the MNIST data. If you use git, then you can get them by cloning the repository of this book:

git clone https://github.com/mnielsen/neural-networks-and-deep-learning.git

If not, download the code from the link .

By the way, when I mentioned MNIST data earlier, I said that they are divided into 60,000 training images and 10,000 test images. This is the official description from MNIST. We will break the data a little differently. We will leave the verification images unchanged, but we will divide the training set into two parts: 50,000 images, which we will use to train the National Assembly, and individual 10,000 images for additional confirmation. While we will not use them, but later they will be useful to us when we will understand the configuration of some hyper parameters of the NS - the learning speed, etc., - which our algorithm does not directly select. Although corroborating data are not part of the original MNIST specification, many use MNIST in this way, and in the field of HC the use of corroborating data is common. Now, speaking of the MNIST training data,

In addition to MNIST data, we also need a python library called Numpy for quick linear algebra calculations . If you do not have it, you can take it from the link .

Before giving you the whole program, let me explain the main features of the code for NS. The central place is occupied by the Network class, which we use to represent the National Assembly. Here is the initialization code for the Network object:

class Network(object):
    def __init__(self, sizes):
        self.num_layers = len(sizes)
        self.sizes = sizes
        self.biases = [np.random.randn(y, 1) for y in sizes[1:]]
        self.weights = [np.random.randn(y, x) 
                        for x, y in zip(sizes[:-1], sizes[1:])]

The sizes array contains the number of neurons in the corresponding layers. So, if we want to create a Network object with two neurons in the first layer, three neurons in the second layer, and one neuron in the third, we will write it like this:

net = Network([2, 3, 1])

The offsets and weights in the Network object are randomly initialized using the numpy function np.random.randn, which generates a Gaussian distribution with a mathematical expectation of 0 and a standard deviation of 1. This random initialization gives our stochastic gradient descent algorithm a starting point. In the following chapters we will find the best ways to initialize weights and offsets, but for now this is enough. Note that the Network initialization code assumes that the first layer of neurons will be input, and does not assign them a bias, since they are only used to calculate the output.

Also note that offsets and weights are stored as an array of Numpy matrices. For example, net.weights [1] is a Numpy matrix that stores weights connecting the second and third layers of neurons (this is not the first and second layers, since in python the numbering of the elements of the array comes from scratch). Since it will take too long to write net.weights [1], we denote this matrix as w. This is such a matrix that w _jk is the weight of the connection between the kth neuron in the second layer and the jth neuron in the third. Such an order of indices j and k may seem strange - wouldn't it be more logical to swap them? But the big advantage of such a record will be that the activation vector of the third layer of neurons is obtained:

$$

Let's look at this pretty rich equation. a is the activation vector of the second layer of neurons. To get a ', we multiply a by the weight matrix w, and add the displacement vector b. Then we apply the sigmoid σ element by element to each element of the vector wa + b (this is called the vectorization of the function σ). It is easy to verify that equation (22) gives the same result as rule (4) for computing a sigmoid neuron.

Exercise

• Write equation (22) in component form, and make sure that it gives the same result as rule (4) for calculating a sigmoid neuron.

With all of this in mind, it's easy to write code that computes the output of a Network object. We start by defining a sigmoid:

def sigmoid(z):
    return 1.0/(1.0+np.exp(-z))

Note that when the z parameter is a Numpy vector or array, Numpy will automatically apply the sigmoid element-wise, that is, in vector form.

Add a direct propagation method to the Network class, which takes a from the network as input and returns the corresponding output. It is assumed that parameter a is (n, 1) Numpy ndarray, not a vector (n,). Here n is the number of input neurons. If you try to use the vector (n,), you will get strange results.

The method simply applies equation (22) to each layer:

    def feedforward(self, a):
        """Вернуть выходные данные сети при входных данных "a""""
        for b, w in zip(self.biases, self.weights):
            a = sigmoid(np.dot(w, a)+b)
        return a

Of course, basically we from Network objects need them to learn. To do this, we will give them the SGD method, which implements stochastic gradient descent. Here is his code. In some places it is rather mysterious, but below we will analyze it in more detail.

    def SGD(self, training_data, epochs, mini_batch_size, eta,
            test_data=None):
        """Обучаем сеть при помощи мини-пакетов и стохастического градиентного спуска. training_data – список кортежей "(x, y)", обозначающих обучающие входные данные и желаемые выходные. Остальные обязательные параметры говорят сами за себя. Если test_data задан, тогда сеть будет оцениваться относительно проверочных данных после каждой эпохи, и будет выводиться текущий прогресс. Это полезно для отслеживания прогресса, однако существенно замедляет работу. """
        if test_data: n_test = len(test_data)
        n = len(training_data)
        for j in xrange(epochs):
            random.shuffle(training_data)
            mini_batches = [
                training_data[k:k+mini_batch_size]
                for k in xrange(0, n, mini_batch_size)]
            for mini_batch in mini_batches:
                self.update_mini_batch(mini_batch, eta)
            if test_data:
                print "Epoch {0}: {1} / {2}".format(
                    j, self.evaluate(test_data), n_test)
            else:
                print "Epoch {0} complete".format(j)

training_data is a list of tuples "(x, y)" representing training input and desired output. The epochs and mini_batch_size variables are the number of epochs to learn and the size of mini-packets to use. eta - learning speed, η. If test_data is set, then the network will be evaluated against the verification data after each era, and the current progress will be displayed. This is useful for tracking progress, but significantly slows down the work.

The code works like this. In each era, he begins by accidentally mixing training data, and then breaks them into mini-packets of the right size. This is an easy way to create a sample of training data. Then for each mini_batch we apply one step of gradient descent. This is done by the self.update_mini_batch code (mini_batch, eta), which updates the network weights and offsets according to a single gradient descent iteration using only training data in mini_batch. Here is the code for the update_mini_batch method:

    def update_mini_batch(self, mini_batch, eta):
        """Обновить веса и смещения сети, применяя градиентный спуск с использованием обратного распространения к одному мини-пакету. mini_batch – это список кортежей (x, y), а eta – скорость обучения."""
        nabla_b = [np.zeros(b.shape) for b in self.biases]
        nabla_w = [np.zeros(w.shape) for w in self.weights]
        for x, y in mini_batch:
            delta_nabla_b, delta_nabla_w = self.backprop(x, y)
            nabla_b = [nb+dnb for nb, dnb in zip(nabla_b, delta_nabla_b)]
            nabla_w = [nw+dnw for nw, dnw in zip(nabla_w, delta_nabla_w)]
        self.weights = [w-(eta/len(mini_batch))*nw 
                        for w, nw in zip(self.weights, nabla_w)]
        self.biases = [b-(eta/len(mini_batch))*nb 
                       for b, nb in zip(self.biases, nabla_b)]

Most of the work is done by the line.

            delta_nabla_b, delta_nabla_w = self.backprop(x, y)

It invokes a backpropagation algorithm — a quick way to compute the gradient of a cost function. So update_mini_batch simply calculates these gradients for each training example from mini_batch, and then updates self.weights and self.biases.

So far, I will not demonstrate code for self.backprop. We will learn about backpropagation in the next chapter, and there will be self.backprop code. For now, suppose it behaves as stated, returning an appropriate gradient for the cost associated with the training example x.

Let's look at the whole program, including explanatory comments. With the exception of the self.backprop function, the program speaks for itself - the main work is done by self.SGD and self.update_mini_batch. The self.backprop method uses several additional functions to calculate the gradient, namely sigmoid_prime, which computes the derivative of the sigmoid, and self.cost_derivative, which I will not describe here. You can get an idea of ​​them by looking at the code and comments. In the next chapter we will consider them in more detail. Keep in mind that while the program seems long, most of the code is comments that make it easier to understand. In fact, the program itself consists of only 74 non-lines of code - not empty and not comments. All code is available on GitHub .

"""
network.py
~~~~~~~~~~
Модуль реализации обучающего алгоритма стохастического градиентного спуска для нейросети прямого распространения. Градиенты вычисляются при помощи обратного распространения. Я специально делал код простым, читаемым и легко модифицируемым. Он не оптимизирован, и в нём нет многих желательных вещей.
"""
#### Библиотеки
# Стандартная библиотека
import random
# Сторонние библиотеки 
import numpy as np
class Network(object):
    def __init__(self, sizes):
        """ Массив sizes содержит количество нейронов в соответствующих слоях. Так что, если мы хотим создать объект Network с двумя нейронами в первом слое, тремя нейронами во втором слое, и одним нейроном в третьем, то мы запишем это, как [2, 3, 1]. Смещения и веса сети инициализируются случайным образом с использованием распределения Гаусса с математическим ожиданием 0 и среднеквадратичным отклонением 1. Предполагается, что первый слой нейронов будет входным, и поэтому у его нейронов нет смещений, поскольку они используются только при подсчёте выходных данных. """
        self.num_layers = len(sizes)
        self.sizes = sizes
        self.biases = [np.random.randn(y, 1) for y in sizes[1:]]
        self.weights = [np.random.randn(y, x)
                        for x, y in zip(sizes[:-1], sizes[1:])]
    def feedforward(self, a):
        """Возвращает выходные данные сети, когда ``a`` - входные данные."""
        for b, w in zip(self.biases, self.weights):
            a = sigmoid(np.dot(w, a)+b)
        return a
    def SGD(self, training_data, epochs, mini_batch_size, eta,
            test_data=None):
        """Обучаем сеть при помощи мини-пакетов и стохастического градиентного спуска. training_data – список кортежей "(x, y)", обозначающих обучающие входные данные и желаемые выходные. Остальные обязательные параметры говорят сами за себя. Если test_data задан, тогда сеть будет оцениваться относительно проверочных данных после каждой эпохи, и будет выводиться текущий прогресс. Это полезно для отслеживания прогресса, однако существенно замедляет работу. """
        if test_data: n_test = len(test_data)
        n = len(training_data)
        for j in xrange(epochs):
            random.shuffle(training_data)
            mini_batches = [
                training_data[k:k+mini_batch_size]
                for k in xrange(0, n, mini_batch_size)]
            for mini_batch in mini_batches:
                self.update_mini_batch(mini_batch, eta)
            if test_data:
                print "Epoch {0}: {1} / {2}".format(
                    j, self.evaluate(test_data), n_test)
            else:
                print "Epoch {0} complete".format(j)
    def update_mini_batch(self, mini_batch, eta):
        """Обновить веса и смещения сети, применяя градиентный спуск с использованием обратного распространения к одному мини-пакету. mini_batch – это список кортежей (x, y), а eta – скорость обучения."""
        nabla_b = [np.zeros(b.shape) for b in self.biases]
        nabla_w = [np.zeros(w.shape) for w in self.weights]
        for x, y in mini_batch:
            delta_nabla_b, delta_nabla_w = self.backprop(x, y)
            nabla_b = [nb+dnb for nb, dnb in zip(nabla_b, delta_nabla_b)]
            nabla_w = [nw+dnw for nw, dnw in zip(nabla_w, delta_nabla_w)]
        self.weights = [w-(eta/len(mini_batch))*nw
                        for w, nw in zip(self.weights, nabla_w)]
        self.biases = [b-(eta/len(mini_batch))*nb
                       for b, nb in zip(self.biases, nabla_b)]
    def backprop(self, x, y):
        """Вернуть кортеж ``(nabla_b, nabla_w)``, представляющий градиент для функции стоимости C_x.  ``nabla_b`` и ``nabla_w`` - послойные списки массивов numpy, похожие на ``self.biases`` and ``self.weights``."""
        nabla_b = [np.zeros(b.shape) for b in self.biases]
        nabla_w = [np.zeros(w.shape) for w in self.weights]
        # прямой проход
        activation = x
        activations = [x] # список для послойного хранения активаций
        zs = [] # список для послойного хранения z-векторов
        for b, w in zip(self.biases, self.weights):
            z = np.dot(w, activation)+b
            zs.append(z)
            activation = sigmoid(z)
            activations.append(activation)
        # обратный проход
        delta = self.cost_derivative(activations[-1], y) * \
            sigmoid_prime(zs[-1])
        nabla_b[-1] = delta
        nabla_w[-1] = np.dot(delta, activations[-2].transpose())
        """Переменная l в цикле ниже используется не так, как описано во второй главе книги. l = 1 означает последний слой нейронов, l = 2 – предпоследний, и так далее. Мы пользуемся преимуществом того, что в python можно использовать отрицательные индексы в массивах."""
        for l in xrange(2, self.num_layers):
            z = zs[-l]
            sp = sigmoid_prime(z)
            delta = np.dot(self.weights[-l+1].transpose(), delta) * sp
            nabla_b[-l] = delta
            nabla_w[-l] = np.dot(delta, activations[-l-1].transpose())
        return (nabla_b, nabla_w)
    def evaluate(self, test_data):
        """Вернуть количество проверочных входных данных, для которых нейросеть выдаёт правильный результат. Выходные данные сети – это номер нейрона в последнем слое с наивысшим уровнем активации."""
        test_results = [(np.argmax(self.feedforward(x)), y)
                        for (x, y) in test_data]
        return sum(int(x == y) for (x, y) in test_results)
    def cost_derivative(self, output_activations, y):
        """Вернуть вектор частных производных (чп C_x / чп a) для выходных активаций."""
        return (output_activations-y)
#### Разные функции
def sigmoid(z):
    """Сигмоида."""
    return 1.0/(1.0+np.exp(-z))
def sigmoid_prime(z):
    """Производная сигмоиды."""
    return sigmoid(z)*(1-sigmoid(z))

How well does the program recognize handwritten numbers? Let's start by loading the MNIST data. We will do this using the small helper program mnist_loader.py, which I will describe below. Run the following commands in the python shell:

>>> import mnist_loader
>>> training_data, validation_data, test_data = \
... mnist_loader.load_data_wrapper()

This, of course, can be done in a separate program, but if you work in parallel with a book, it will be easier.

After downloading the MNIST data, set up a network of 30 hidden neurons. We will do this after importing the program described above, which is called network:

>>> import network
>>> net = network.Network([784, 30, 10])

Finally, we use stochastic gradient descent for training on training data for 30 eras, with a mini-packet size of 10, and a learning speed of η = 3.0:

>>> net.SGD(training_data, 30, 10, 3.0, test_data=test_data)

If you are executing code in parallel with reading a book, keep in mind that it will take several minutes to execute. I suggest you start everything, continue reading, and periodically check what the program produces. If you are in a hurry, you can reduce the number of eras by reducing the number of hidden neurons, or by using only part of the training data. The final working code will work faster: these python scripts are designed to make you understand how the network works, and are not high-performance! And, of course, after training, the network can work very quickly on almost any computing platform. For example, when we teach the network a good selection of weights and offsets, it can be easily ported to work on JavaScript in a web browser, or as a native application on a mobile device. Anyway, approximately this conclusion is given by the program that trains the neural network. She writes the number of correctly recognized test images after each era of training. As you can see, even after one era, it reaches an accuracy of 9,129 out of 10,000, and this number continues to grow:

Epoch 0: 9129 / 10000
Epoch 1: 9295 / 10000
Epoch 2: 9348 / 10000
...
Epoch 27: 9528 / 10000
Epoch 28: 9542 / 10000
Epoch 29: 9534 / 10000

It turns out that the trained network gives a percentage of correct classification of about 95 - 95.42% at maximum! A pretty promising first attempt. I warn you that your code will not necessarily produce exactly the same results, since we initialize the network with random weights and offsets. For this chapter, I have chosen the best of three attempts.

Let's restart the experiment by changing the number of hidden neurons to 100. As before, if you run the code at the same time as reading, keep in mind that it takes quite a lot of time (on my machine, each era takes several tens of seconds), so it’s better to read in parallel with code execution.

>>> net = network.Network([784, 100, 10])
>>> net.SGD(training_data, 30, 10, 3.0, test_data=test_data)

Naturally, this improves the result to 96.59%. At least in this case, using more hidden neurons helps to get better results.

Feedback from readers suggests that the results of this experiment vary greatly, and some learning outcomes are much worse. Using techniques from Chapter 3 to seriously reduce the diversity of work efficiency from one run to another.

Of course, in order to achieve such accuracy, I had to choose a certain number of eras for learning, the size of the mini-package and the learning speed η. As I mentioned above, they are called hyperparameters of our National Assembly - to distinguish them from simple parameters (weights and offsets) that the algorithm adjusts during training. If we choose hyperparameters poorly, we will get poor results. Suppose, for example, that we have chosen the learning rate η = 0.001:

>>> net = network.Network([784, 100, 10])
>>> net.SGD(training_data, 30, 10, 0.001, test_data=test_data)

The results will be much less impressive: However, you can see that network efficiency is slowly growing over time. This suggests that you can try to increase the learning speed, for example, to 0.01. In this case, the results will be better, which indicates the need to further increase the speed (if the change improves the situation, change further!). If you do this several times, we will eventually arrive at η = 1.0 (and sometimes even 3.0), which is close to our earlier experiments. So, although we initially poorly selected hyperparameters, at least we gathered enough information to be able to improve our choice of parameters.

Epoch 0: 1139 / 10000
Epoch 1: 1136 / 10000
Epoch 2: 1135 / 10000
...
Epoch 27: 2101 / 10000
Epoch 28: 2123 / 10000
Epoch 29: 2142 / 10000



In general, debugging NA is a complicated matter. This is especially so when the choice of initial hyperparameters produces results that do not exceed random noise. Suppose we try to use a successful architecture of 30 neurons, but change the learning speed to 100.0:

>>> net = network.Network([784, 30, 10])
>>> net.SGD(training_data, 30, 10, 100.0, test_data=test_data)

In the end, it turns out that we went too far and took too much speed: Now imagine that we are approaching this task for the first time. Of course, we know from early experiments that it would be right to reduce the speed of learning. But if we were to approach this task for the first time, we would not have output that could lead us to the right solution. Could we start thinking that perhaps we have chosen the wrong initial parameters for weights and offsets, and it is difficult for the network to learn? Or maybe we do not have enough training data to get a meaningful result? Perhaps we did not wait enough eras? Perhaps a neural network with such an architecture simply cannot learn to recognize handwritten numbers? Perhaps the learning speed is too slow? When you first approach the task, you never have confidence.

Epoch 0: 1009 / 10000
Epoch 1: 1009 / 10000
Epoch 2: 1009 / 10000
Epoch 3: 1009 / 10000
...
Epoch 27: 982 / 10000
Epoch 28: 982 / 10000
Epoch 29: 982 / 10000



From this it is worth learning a lesson that debugging NS is not a trivial task, and this, like regular programming, is part of the art. You must learn this debugging art in order to get good results from NS. In general, we need to develop a heuristic to select good hyperparameters and good architecture. We will discuss this in detail in the book, including how I selected the above hyperparameters.

Exercise

• Try to create a network of only two layers - input and output, without hidden - with 784 and 10 neurons, respectively. Train the network with stochastic gradient descent. What classification accuracy do you get?

I previously skipped the details of loading MNIST data. It happens quite simply. Here is the code to complete the picture. Data structures are described in the comments - everything is simple, tuples and arrays of Numpy ndarray objects (if you are not familiar with such objects, imagine them as vectors).

"""
mnist_loader
~~~~~~~~~~~~
Библиотека загрузки изображений из базы MNIST. Детали структур описаны в комментариях к ``load_data`` и ``load_data_wrapper``.  На практике, ``load_data_wrapper`` - это функция, которую обычно вызывает код НС.
"""
#### Библиотеки
# Стандартные
import cPickle
import gzip
# Сторонние 
import numpy as np
def load_data():
    """Вернуть данные MNIST в виде кортежа, содержащего обучающие, подтверждающие и проверочные данные. ``training_data`` возвращается как кортеж с двумя вхождениями. 
Первое содержит сами картинки. Это numpy ndarray с 50 000 элементами. Каждый элемент – это в свою очередь numpy ndarray с 784 значениями, представляющими 28 * 28 = 784 пикселя одного изображения MNIST.
Второе – это numpy ndarray с 50 000 элементами. Эти элементы – цифры от 0 до 9 для соответствующих изображений, содержащихся в первом вхождении.
``validation_data`` и ``test_data`` похожи, только содержат по 10 000 изображений.
Это удобный формат данных, но для использования в НС полезно будет немного изменить формат ``training_data``. Это делается в функции-обёртке ``load_data_wrapper()``.
    """
    f = gzip.open('../data/mnist.pkl.gz', 'rb')
    training_data, validation_data, test_data = cPickle.load(f)
    f.close()
    return (training_data, validation_data, test_data)
def load_data_wrapper():
    """Вернуть кортеж, содержащий ``(training_data, validation_data, test_data)``. На основе ``load_data``, но формат удобнее для использования в нашей реализации НС.
В частности, ``training_data`` - это список из  50 000 кортежей из двух переменных, ``(x, y)``.  ``x`` - это 784-размерный numpy.ndarray, содержащий входящее изображение. ``y`` - это 10-мерный numpy.ndarray, представляющий единичный вектор, соответствующий правильной цифре для ``x``.
``validation_data`` и ``test_data`` - это списки, содержащие по 10 000 кортежей из двух переменных, ``(x, y)``.  ``x`` - это 784-размерный numpy.ndarray, содержащий входящее изображение, а ``y`` - это соответствующая классификация, то есть, цифровые значения (целые числа), соответствующие ``x``.
Очевидно, это означает, что для тренировочных и подтверждающих данных мы используем немного разные форматы. Они оказываются наиболее удобными для использования в коде НС."""
    tr_d, va_d, te_d = load_data()
    training_inputs = [np.reshape(x, (784, 1)) for x in tr_d[0]]
    training_results = [vectorized_result(y) for y in tr_d[1]]
    training_data = zip(training_inputs, training_results)
    validation_inputs = [np.reshape(x, (784, 1)) for x in va_d[0]]
    validation_data = zip(validation_inputs, va_d[1])
    test_inputs = [np.reshape(x, (784, 1)) for x in te_d[0]]
    test_data = zip(test_inputs, te_d[1])
    return (training_data, validation_data, test_data)
def vectorized_result(j):
    """Вернуть 10-мерный единичный вектор с 1.0 в позиции j и нулями на остальных позициях. Это используется для преобразования цифры (0..9) в соответствующие выходные данные НС."""
    e = np.zeros((10, 1))
    e[j] = 1.0
    return e

I said that our program is achieving pretty good results. What does this mean? Good compared to what? It is useful to have the results of some simple, basic tests with which you could make a comparison to understand what “good results” mean. The simplest base level, of course, would be a random guess. This can be done in about 10% of cases. And we show a much better result!

What about a less trivial base level? Let's look at how dark the picture is. For example, image 2 will usually be darker than image 1, simply because it has more dark pixels, as seen in the examples below:



It follows that we can calculate the average darkness for each digit from 0 to 9. When we get a new image, we calculate its darkness, and we guess that it shows a figure with the nearest average darkness. This is a simple procedure that is easy to program, so I will not write code - if interested, it lies on GitHub . But this is a serious improvement compared to random guesses - the code correctly recognizes 2,225 of 10,000 images, that is, it gives an accuracy of 22.25%.

It is not difficult to find other ideas that achieve accuracy in the range from 20 to 50%. After working a little more, you can exceed 50%. But to achieve much greater accuracy, it is better to use authoritative MO algorithms. Let's try one of the most famous algorithms, the support vector method or SVM. If you are unfamiliar with SVM, don’t worry, we don’t need to understand these details. We just use a python library called scikit-learn, which provides a simple interface to the fast C library for SVM, known as LIBSVM .

If we run the SVM classifier scikit-learn at the default settings, then we get the correct classification of 9,435 out of 10,000 (the code is available at the link) This is already a big improvement over the naive approach of classifying images by darkness. This means that SVM works about as good as our NS, only a little worse. In the following chapters we will get acquainted with new techniques that will allow us to improve our NS so that they greatly outperform SVM.

But that is not all. Result 9 435 out of 10 000 from scikit-learn is specified for the default settings. SVM has many parameters that can be tuned, and you can look for parameters that improve this result. I will not go into details, they can be read in the articleAndreas Muller. He showed that by doing work to optimize the parameters, it is possible to achieve an accuracy of at least 98.5%. In other words, a well-tuned SVM makes only one digit out of 70 errors. A good result! Can NA achieve more?

It turns out they can. Today, a well-tuned NS overtakes any other known technology in the MNIST solution, including SVM. The record for 2013 correctly classified 9,979 out of 10,000 images. And we will see most of the technologies used for this in this book. This level of accuracy is close to human, and perhaps even exceeds it, since several images from MNIST are difficult to decipher even for humans, for example:



I think you will agree that they are difficult to classify! With such images in the MNIST dataset, it is surprising that the NS can correctly recognize all the images from 10,000, except 21. Usually, programmers consider that a complex algorithm is required to solve such a complex task. But even NS in the work of the record holder use fairly simple algorithms, which are small variations of those that we examined in this chapter. All complexity automatically appears during training based on training data. In a sense, the moral of our results and those contained in more complex works is that for some tasks

complex algorithm ≤ simple training algorithm + good training data

To deep learning

Although our network is showing impressive performance, it is achieved in a mysterious way. Weights and mixing networks are automatically detected. So, we do not have a ready-made explanation of how the network does what it does. Is there any way to understand the basic principles of classification by a network of handwritten numbers? And is it possible, given them, to improve the result?

We reformulate these questions more strictly: let us assume that in a few decades the NS will turn into artificial intelligence (AI). Will we understand how this AI works? Perhaps the networks will remain incomprehensible to us, with their weights and offsets, since they are assigned automatically. In the early years of AI research, people hoped that trying to create AI would also help us understand the principles underlying intelligence, and maybe even the work of the human brain. However, in the end it may turn out that we will not understand either the brain or how the AI ​​works!

To deal with these issues, let's recall the interpretation of artificial neurons that I gave at the beginning of the chapter — that this is a way to weigh evidence. Suppose we want to determine if a person’s face is on an image:







This problem can be approached in the same way as handwriting recognition: using image pixels as input for the NS, and the output of the NS will be one neuron that will say, “Yes, this is a face”, or “No, this is not a face ".

Suppose we do this, but without using a learning algorithm. We will try to manually create a network, choosing the appropriate weights and offsets. How can we approach this? For a moment, forgetting about the National Assembly, we could divide the task into subtasks: does the image of the eyes have in the upper left corner? Is there an eye in the upper right corner? Is there a middle nose? Is there a mouth down the middle? Is there hair at the top? Etc.

If the answers to several of these questions are positive, or even “probably yes,” then we conclude that the image may have a face. Conversely, if the answers are no, then there is probably no person.

This, of course, is an approximate heuristic, and it has many shortcomings. Perhaps this is a bald man, and he does not have hair. Perhaps we can see only part of the face, or the face at an angle, so that some parts of the face are closed. Nevertheless, heuristic suggests that if we can solve subproblems with the help of neural networks, then perhaps we can create NSs for face recognition by combining networks for subtasks. The following is a possible architecture of such a network in which subnets are indicated by rectangles. This is not a completely realistic approach to solving the face recognition problem: it is needed to help us intuitively understand the work of neural networks.


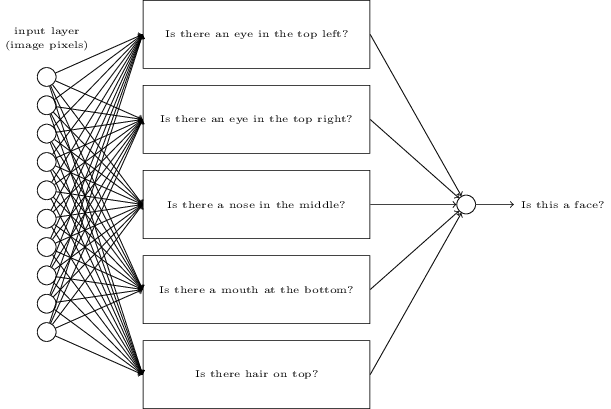
In the rectangles there are subtasks: does the image of the eyes have in the upper left corner? Is there an eye in the upper right corner? Is there a middle nose? Is there a mouth down the middle? Is there hair at the top? Etc.

It is possible that subnets can also be disassembled into components. Take the question of having an eye in the upper left corner. It can be disassembled into questions such as: “Is there an eyebrow?”, “Are there eyelashes?”, “Is there a pupil?” And so on. Of course, the questions should contain information about the location - "Is the eyebrow located on the upper left, above the pupil?", And so on - but let's simplify it for now. Therefore, the network that answers the question about the presence of the eye can be disassembled into the components:


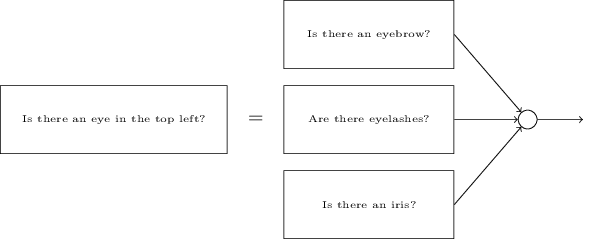
“Is there an eyebrow?”, “Are there eyelashes?”, “Is there a pupil?”

These questions can be further broken down into small ones, in steps through many layers. As a result, we will work with subnets that answer such simple questions that they can easily be disassembled at the pixel level. These questions may concern, for example, the presence or absence of simple forms in certain places of the image. Individual neurons associated with pixels will be able to respond to them.

The result is a network that breaks down very complex questions — whether a person is in the image — into very simple questions that can be answered at the individual pixel level. She will do this through a sequence of many layers, in which the first layers answer very simple and specific questions about the image, and the latter create a hierarchy of more complex and abstract concepts. Networks with such a multilayer structure - two or more hidden layers - are called deep neural networks (GNS).

Of course, I did not talk about how to do this recursive subnetting. It will definitely be impractical to manually select weights and offsets. We would like to use training algorithms so that the network automatically learns weights and offsets - and through them the hierarchies of concepts - based on training data. Researchers in the 1980s and 1990s tried to use stochastic gradient descent and backpropagation to train GNS. Unfortunately, with the exception of a few special architectures, they did not succeed. The networks trained, but very slowly, and in practice it was too slow for it to be used somehow.

Since 2006, several technologies have been developed to train STS. They are based on stochastic gradient descent and back propagation, but they also contain new ideas. They allowed to train much deeper networks - today people quietly train networks with 5-10 layers. And it turns out that they solve many problems much better than shallow NSs, that is, networks with one hidden layer. The reason, of course, is that STS can create a complex hierarchy of concepts. This is similar to how programming languages ​​use modular schemes and abstraction ideas so that they can create complex computer programs. To compare a deep NS with a shallow NS is approximately how to compare a programming language that can make function calls with a language that does not. Abstraction in the NS does not look like in programming languages,