How to solve NP-hard problems using parameterized algorithms
Research work is perhaps the most interesting part of our training. The idea is to try yourself in the chosen direction even at the university. For example, students from the areas of Software Engineering and Machine Learning often go to do research in the company (mainly JetBrains or Yandex, but not only).
In this post I will talk about my project in Computer Science. As part of the work, I studied and put into practice approaches to solving one of the most famous NP-hard problems: the vertex covering problem .
Now an interesting approach to NP-difficult problems is developing rapidly - parameterized algorithms. I will try to get you up to speed, tell some simple parameterized algorithms and describe one powerful method that helped me a lot. I presented my results at the PACE Challenge: according to the results of open tests, my decision is in third place, and the final results will be known on July 1.

My name is Vasily Alferov, I am now completing the third year of HSE - St. Petersburg. I have been fond of algorithms since school times, when I studied at Moscow school 179 and successfully participated in computer science competitions.
An example is taken from the book “Parameterized algorithms”.
Imagine that you are a bar guard in a small town. Every Friday, half of the city comes to your bar to relax, which gives you a lot of trouble: you need to throw violent visitors out of the bar to prevent fights. In the end, it bothers you and you decide to take preventive measures.
Since your city is small, you know for sure which pairs of visitors are very likely to wrangle if they get to the bar together. You have a list of n people who will come to the bar tonight. You decide not to let any townspeople into the bar so that no one fights. At the same time, your superiors do not want to lose profits and will be unhappy if you do not let more than k into the barhuman.
Unfortunately, the challenge you are facing is a classic NP-hard task. You could know it as Vertex Cover , or as a vertex coverage problem. For such problems, in the general case, algorithms that work in an acceptable time are unknown. To be precise, the unproven and fairly strong hypothesis ETH (Exponential Time Hypothesis) says that this problem can not be solved in time , that is, what is noticeably better than exhaustive search can not be thought of. For example, let n = 1000 people plan to come to your bar . Then a complete search will be
, that is, what is noticeably better than exhaustive search can not be thought of. For example, let n = 1000 people plan to come to your bar . Then a complete search will be options that there are roughly
options that there are roughly  - insanely much. Fortunately, your guide set you a k = 10 limit , so the number of combinations you need to iterate over is much less: the number of subsets of ten elements is
- insanely much. Fortunately, your guide set you a k = 10 limit , so the number of combinations you need to iterate over is much less: the number of subsets of ten elements is . This is already better, but still does not count for the day, even on a powerful cluster.
. This is already better, but still does not count for the day, even on a powerful cluster.
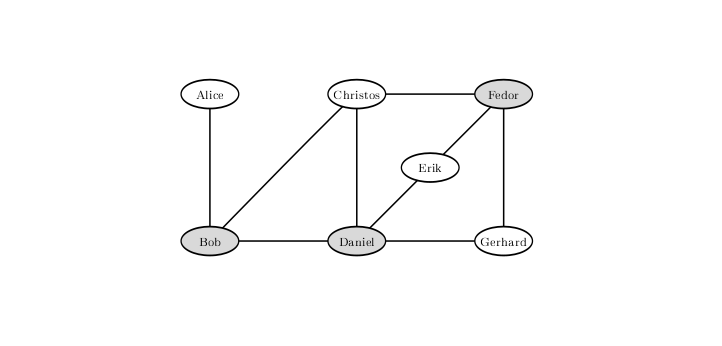
To exclude the possibility of a fight with such a configuration of strained relations between visitors to the bar, you must not let Bob, Daniel and Fedor. A solution in which only two are left overboard does not exist.
Does this mean it's time to surrender and let everyone in? Let's consider other options. Well, for example, you can not let in only those who are likely to fight with a very large number of people. If someone can fight with at least k + 1 by another person, then you definitely cannot let him in, otherwise you will have to not let all k + 1 townspeople with whom he can fight, which will definitely upset the leadership.
May you throw out all you could according to this principle. Then everyone else can fight with no more than k people. Throwing k people out of them , you can prevent no more than conflicts. So, if all more than
conflicts. So, if all more than if a person is involved in at least one conflict, then you certainly cannot prevent them all. Since, of course, you are sure to let completely non-conflict people go, then you need to sort out all subsets the size of ten out of two hundred people. There are approximately
if a person is involved in at least one conflict, then you certainly cannot prevent them all. Since, of course, you are sure to let completely non-conflict people go, then you need to sort out all subsets the size of ten out of two hundred people. There are approximately , and so many operations can already be sorted out on the cluster.
, and so many operations can already be sorted out on the cluster.
If it is safe to take completely non-conflicting personalities, what about those who are involved in only one conflict? In fact, they can also be let in by closing the doors in front of their opponent. Indeed, if Alice conflicts only with Bob, then if we let in two of them, Alice, we will not lose: Bob may have other conflicts, but Alice definitely doesn’t. Moreover, it makes no sense for us not to let both. After such operations, no more guests with an unresolved fate: all we have
guests with an unresolved fate: all we have  conflicts, in each of two participants and each involved in at least two. So, it remains only to sort out
conflicts, in each of two participants and each involved in at least two. So, it remains only to sort out options, which may well be calculated for half a day on a laptop.
options, which may well be calculated for half a day on a laptop.
In fact, simple reasoning can achieve even more attractive conditions. Note that we definitely need to resolve all disputes, that is, from each conflicting pair to choose at least one person whom we will not let in. Consider this algorithm: take any conflict from which we delete one participant and start recursively from the remainder, then delete another and also start recursively. Since we throw someone at every step, the recursion tree of such an algorithm is a binary tree of depth k , therefore, in total, the algorithm works for where n is the number of vertices and m is the number of edges. In our example, this is about ten million, which in a split second will be counted not only on a laptop, but even on a mobile phone.
where n is the number of vertices and m is the number of edges. In our example, this is about ten million, which in a split second will be counted not only on a laptop, but even on a mobile phone.
The above example is an example of a parameterized algorithm . Parametrized algorithms are algorithms that work during f (k) poly (n) , where p is a polynomial, f is an arbitrary computable function, and k is some parameter that, quite possibly, will be much smaller than the size of the problem.
All considerations prior to this algorithm give an example of kernel kernelization.- one of the common techniques for creating parameterized algorithms. Kernelization is a reduction in the size of a task to a value limited by a function of a parameter. The resulting task is often called the kernel. So, by simple reasoning about degrees of vertices, we got a quadratic kernel for the Vertex Cover problem, parameterized by the size of the answer. There are other parameters that can be selected for this task (for example, Vertex Cover Above LP), but we will discuss just such a parameter.
The PACE Challenge (The Parameterized Algorithms and Computational Experiments Challenge) competition began in 2015 to establish a connection between parameterized algorithms and approaches used in practice to solve computational problems. The first three competitions were devoted to finding the tree width of the graph ( Treewidth ), finding the Steiner Tree ( Steiner Tree ) and finding many vertices, cutting cycles ( Feedback Vertex Set ). This year, one of the tasks in which one could try one's strengths was the problem of top cover described above.
Competition is gaining popularity every year. If you believe the preliminary data, then this year only 24 teams took part in the competition to solve the problem of vertex coverage. It is worth noting that the competition does not last several hours, and not even a week, but several months. Teams have the opportunity to study literature, come up with their original idea and try to implement it. In fact, this competition is a research work. Ideas for the most effective solutions and rewarding of winners will be held in conjunction with the IPEC (International Symposium on Parameterized and Exact Computation) conference at the largest annual algorithmic meeting in Europe ALGO . More information about the competition itself can be found on the website., and the results of past years are here .
To cope with the problem of vertex coverage, I tried to apply parameterized algorithms. They usually consist of two parts: simplification rules (which ideally lead to kernelization) and splitting rules. Simplification rules are preprocessing input in polynomial time. The purpose of applying such rules is to reduce the problem to an equivalent problem of a smaller size. Simplification rules are the most expensive part of the algorithm, and the application of this particular part leads to the total time of work instead of simple polynomial time. In our case, the splitting rules are based on the fact that for each vertex you need to take either her or her neighbor in response.
instead of simple polynomial time. In our case, the splitting rules are based on the fact that for each vertex you need to take either her or her neighbor in response.
The general scheme is this: we apply the simplification rules, then we select some vertex, and we make two recursive calls: in the first we take it in response, and in the other we take all its neighbors. This is what we call splitting (brunching) along this peak.
Exactly one addition will be made to this scheme in the next paragraph.
Let's discuss how to choose a vertex along which splitting will occur.
The main idea is very greedy in the algorithmic sense: let's take the peak of the maximum degree and split it by it. Why does it seem so better? Because in the second branch of the recursive call, we will remove so many vertices in this way. You can expect that a small graph will remain and we will work on it quickly.
This approach, with the simple techniques of kernelization already discussed, is not bad, it solves some tests with a size of several thousand vertices. But, for example, it does not work well for cubic graphs (that is, graphs whose degree of each vertex is three).
There is another idea based on a fairly simple idea: if the graph is disconnected, the problem on its connected components can be solved independently by combining the answers at the end. This, by the way, is the small promised modification in the scheme, which will significantly speed up the solution: earlier in this case we worked for the product of the times of counting the responses of the components, and now we work for the amount. And to speed up the brunching, you need to turn a connected graph into a disconnected one.
How to do it? If there is an articulation point in the graph, it is necessary to wander along it. An articulation point is such a vertex that, when removed, the graph loses connectivity. Find in the graph all the points of the joint can be a classical algorithm in linear time. This approach significantly speeds up brunching.

When you remove any of the selected vertices, the graph decomposes into connected components.
We will do it, but I want more. For example, look for small vertex sections in the graph and split along the vertices from it. The most effective way I know to find the minimum global vertex section is to use the Gomori-Hu tree, which is built in cubic time. In the PACE Challenge, a typical graph size is several thousand vertices. In this scenario, billions of operations need to be performed at each vertex of the recursion tree. It turns out that it is simply impossible to solve the problem in the allotted time.
Let's try to optimize the solution. The minimum vertex section between a pair of vertices can be found by any algorithm constructing the maximum flow. You can let Dinits algorithm onto such a networkIn practice, it works very fast. I have a suspicion that theoretically it is possible to prove an estimate for the time of work that is already quite acceptable.
that is already quite acceptable.
I tried several times to search for cuts between pairs of random vertices and take the most balanced one from them. Unfortunately, in the open PACE Challenge tests this gave poor results. I compared it with an algorithm that was scattered along the vertices of the maximum degree, starting them with a restriction on the depth of descent. After the algorithm trying to find the cut in this way, there remained larger graphs. This is due to the fact that the cuts turned out to be very unbalanced: after removing 5-10 peaks, only 15-20 were able to be split off.
It is worth noting that articles on theoretically the fastest algorithms use much more advanced techniques for selecting vertices for splitting. Such techniques have a very complex implementation and often poor grades of time and memory. I could not distinguish from them quite acceptable for practice.
We already have ideas for kernelization. Let me remind you:
With the first two everything is clear, with the third there is one trick. If in the comic bar problem we were given a restriction from above on k , then in the PACE Challenge you just need to find the vertex cover of the minimum size. This is a typical transformation of a Search Problem into a Decision Problem, often between the two types of tasks they do not make a difference. In practice, if we write a vertex coverage problem solver, there may be a difference. For example, as in the third paragraph.
In terms of implementation, there are two ways to do this. The first approach is called Iterative Deepening. It consists in the following: we can start with some reasonable restriction from below on the answer, and then run our algorithm, using this restriction as a restriction on the answer from above, without going down in recursion lower than this restriction. If we find some answer, it is guaranteed to be optimal, otherwise you can increase this limit by one and start again.
Another approach is to store some current optimal answer and look for a smaller answer, when found, change this parameter k to cut off excess branches in the search more.
After conducting some nightly experiments, I settled on a combination of these two methods: first, I run my algorithm with some kind of restriction on the search depth (choosing it so that it takes an insignificant time compared to the main solution) and use the best solution found as a restriction from above to the answer - that is, to that very k .
With vertices of degrees 0 and 1 we figured out. It turns out that this can also be done with vertices of degree 2, but for this, the graph will require more complex operations.
To explain this, you need to somehow identify the peaks. We call a vertex of degree 2 the vertex v , and its neighbors the vertices x and y . Then we will have two cases.
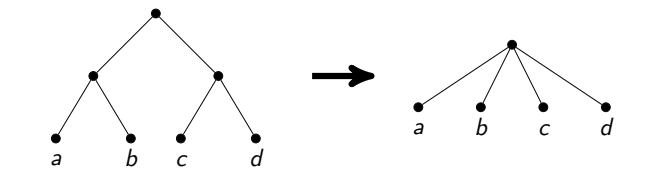
It is worth noting that such an approach for honest linear time is quite difficult to accurately implement. Gluing vertices is a difficult operation, you need to copy the lists of neighbors. If you do this carelessly, you can get asymptotically non-optimal operating time (for example, if you copy a lot of edges after each gluing). I settled on searching for whole paths from vertices of degree 2 and parsing a bunch of special cases, like loops from such vertices or from all such vertices except one.
In addition, it is necessary that this operation be reversible, so that during the return from recursion we restore the graph in its original form. To ensure this, I did not clear the lists of edges of the merged vertices, after which I just knew which edges should be directed to. This implementation of graphs also requires accuracy, but it provides honest linear time. And for graphs of several tens of thousands of edges, it completely fits into the processor cache, which gives great speed advantages.
Finally, the most interesting part of the kernel.
First, recall that in bipartite graphs, the minimum vertex coverage can be sought for . To do this, use the Hopcroft-Karp algorithm to find the maximum matching there, and then use the Koenig-Egerwari theorem .
. To do this, use the Hopcroft-Karp algorithm to find the maximum matching there, and then use the Koenig-Egerwari theorem .
The idea of a linear kernel is as follows: first we divide the graph, that is, instead of each vertex v, we get two vertices and
and  , and instead of each edge u - v we have two edges
, and instead of each edge u - v we have two edges and
and  . The resulting graph will be bipartite. We find in it the minimum vertex coverage. Some vertices of the original graph get there twice, some only once, and some never once. The Nemhauser-Trotter theorem states that in this case it is possible to remove vertices that have not been hit once and to answer those that hit twice. Moreover, she says that of the remaining peaks (those that hit once) you need to take at least half back.
. The resulting graph will be bipartite. We find in it the minimum vertex coverage. Some vertices of the original graph get there twice, some only once, and some never once. The Nemhauser-Trotter theorem states that in this case it is possible to remove vertices that have not been hit once and to answer those that hit twice. Moreover, she says that of the remaining peaks (those that hit once) you need to take at least half back.
We just learned to leave no more than 2k vertices in a graph . Indeed, if the remainder of the answer is at least half of all the vertices, then the total vertices there are no more than 2k .
Here I managed to take a small step forward. It is clear that the kernel constructed in this way depends on what kind of minimum vertex coverage in the bipartite graph we took. I would like to take such that the number of remaining vertices is minimal. Previously, they only knew how to do it in time. . I came up with the implementation of this algorithm in time
. I came up with the implementation of this algorithm in time Thus, this core can be searched on graphs of hundreds of thousands of vertices at each stage of branching.
Thus, this core can be searched on graphs of hundreds of thousands of vertices at each stage of branching.
Practice shows that my solution works well on tests of several hundred vertices and several thousand edges. On such tests, it can be expected that a solution can be found in half an hour. The probability of finding an answer in an acceptable time period increases in principle if the graph has a lot of vertices of a large degree, for example, degrees 10 and above.
To participate in the competition, decisions had to be sent to optil.io . Judging by the plate presented there , my decision on open tests ranks third out of twenty with a wide margin from the second. To be completely honest, it’s not entirely clear how decisions will be evaluated at the competition itself: for example, my decision passes fewer tests than the decision in fourth place, but it works faster for those that pass.
Results on closed tests will be announced on July 1.
In this post I will talk about my project in Computer Science. As part of the work, I studied and put into practice approaches to solving one of the most famous NP-hard problems: the vertex covering problem .
Now an interesting approach to NP-difficult problems is developing rapidly - parameterized algorithms. I will try to get you up to speed, tell some simple parameterized algorithms and describe one powerful method that helped me a lot. I presented my results at the PACE Challenge: according to the results of open tests, my decision is in third place, and the final results will be known on July 1.

About myself
My name is Vasily Alferov, I am now completing the third year of HSE - St. Petersburg. I have been fond of algorithms since school times, when I studied at Moscow school 179 and successfully participated in computer science competitions.
The final number of specialists in parameterized algorithms go to the bar ...
An example is taken from the book “Parameterized algorithms”.
Imagine that you are a bar guard in a small town. Every Friday, half of the city comes to your bar to relax, which gives you a lot of trouble: you need to throw violent visitors out of the bar to prevent fights. In the end, it bothers you and you decide to take preventive measures.
Since your city is small, you know for sure which pairs of visitors are very likely to wrangle if they get to the bar together. You have a list of n people who will come to the bar tonight. You decide not to let any townspeople into the bar so that no one fights. At the same time, your superiors do not want to lose profits and will be unhappy if you do not let more than k into the barhuman.
Unfortunately, the challenge you are facing is a classic NP-hard task. You could know it as Vertex Cover , or as a vertex coverage problem. For such problems, in the general case, algorithms that work in an acceptable time are unknown. To be precise, the unproven and fairly strong hypothesis ETH (Exponential Time Hypothesis) says that this problem can not be solved in time

To exclude the possibility of a fight with such a configuration of strained relations between visitors to the bar, you must not let Bob, Daniel and Fedor. A solution in which only two are left overboard does not exist.
Does this mean it's time to surrender and let everyone in? Let's consider other options. Well, for example, you can not let in only those who are likely to fight with a very large number of people. If someone can fight with at least k + 1 by another person, then you definitely cannot let him in, otherwise you will have to not let all k + 1 townspeople with whom he can fight, which will definitely upset the leadership.
May you throw out all you could according to this principle. Then everyone else can fight with no more than k people. Throwing k people out of them , you can prevent no more than
If it is safe to take completely non-conflicting personalities, what about those who are involved in only one conflict? In fact, they can also be let in by closing the doors in front of their opponent. Indeed, if Alice conflicts only with Bob, then if we let in two of them, Alice, we will not lose: Bob may have other conflicts, but Alice definitely doesn’t. Moreover, it makes no sense for us not to let both. After such operations, no more
In fact, simple reasoning can achieve even more attractive conditions. Note that we definitely need to resolve all disputes, that is, from each conflicting pair to choose at least one person whom we will not let in. Consider this algorithm: take any conflict from which we delete one participant and start recursively from the remainder, then delete another and also start recursively. Since we throw someone at every step, the recursion tree of such an algorithm is a binary tree of depth k , therefore, in total, the algorithm works for
The above example is an example of a parameterized algorithm . Parametrized algorithms are algorithms that work during f (k) poly (n) , where p is a polynomial, f is an arbitrary computable function, and k is some parameter that, quite possibly, will be much smaller than the size of the problem.
All considerations prior to this algorithm give an example of kernel kernelization.- one of the common techniques for creating parameterized algorithms. Kernelization is a reduction in the size of a task to a value limited by a function of a parameter. The resulting task is often called the kernel. So, by simple reasoning about degrees of vertices, we got a quadratic kernel for the Vertex Cover problem, parameterized by the size of the answer. There are other parameters that can be selected for this task (for example, Vertex Cover Above LP), but we will discuss just such a parameter.
Pace challenge
The PACE Challenge (The Parameterized Algorithms and Computational Experiments Challenge) competition began in 2015 to establish a connection between parameterized algorithms and approaches used in practice to solve computational problems. The first three competitions were devoted to finding the tree width of the graph ( Treewidth ), finding the Steiner Tree ( Steiner Tree ) and finding many vertices, cutting cycles ( Feedback Vertex Set ). This year, one of the tasks in which one could try one's strengths was the problem of top cover described above.
Competition is gaining popularity every year. If you believe the preliminary data, then this year only 24 teams took part in the competition to solve the problem of vertex coverage. It is worth noting that the competition does not last several hours, and not even a week, but several months. Teams have the opportunity to study literature, come up with their original idea and try to implement it. In fact, this competition is a research work. Ideas for the most effective solutions and rewarding of winners will be held in conjunction with the IPEC (International Symposium on Parameterized and Exact Computation) conference at the largest annual algorithmic meeting in Europe ALGO . More information about the competition itself can be found on the website., and the results of past years are here .
Solution scheme
To cope with the problem of vertex coverage, I tried to apply parameterized algorithms. They usually consist of two parts: simplification rules (which ideally lead to kernelization) and splitting rules. Simplification rules are preprocessing input in polynomial time. The purpose of applying such rules is to reduce the problem to an equivalent problem of a smaller size. Simplification rules are the most expensive part of the algorithm, and the application of this particular part leads to the total time of work
The general scheme is this: we apply the simplification rules, then we select some vertex, and we make two recursive calls: in the first we take it in response, and in the other we take all its neighbors. This is what we call splitting (brunching) along this peak.
Exactly one addition will be made to this scheme in the next paragraph.
Ideas for splitting rules
Let's discuss how to choose a vertex along which splitting will occur.
The main idea is very greedy in the algorithmic sense: let's take the peak of the maximum degree and split it by it. Why does it seem so better? Because in the second branch of the recursive call, we will remove so many vertices in this way. You can expect that a small graph will remain and we will work on it quickly.
This approach, with the simple techniques of kernelization already discussed, is not bad, it solves some tests with a size of several thousand vertices. But, for example, it does not work well for cubic graphs (that is, graphs whose degree of each vertex is three).
There is another idea based on a fairly simple idea: if the graph is disconnected, the problem on its connected components can be solved independently by combining the answers at the end. This, by the way, is the small promised modification in the scheme, which will significantly speed up the solution: earlier in this case we worked for the product of the times of counting the responses of the components, and now we work for the amount. And to speed up the brunching, you need to turn a connected graph into a disconnected one.
How to do it? If there is an articulation point in the graph, it is necessary to wander along it. An articulation point is such a vertex that, when removed, the graph loses connectivity. Find in the graph all the points of the joint can be a classical algorithm in linear time. This approach significantly speeds up brunching.

When you remove any of the selected vertices, the graph decomposes into connected components.
We will do it, but I want more. For example, look for small vertex sections in the graph and split along the vertices from it. The most effective way I know to find the minimum global vertex section is to use the Gomori-Hu tree, which is built in cubic time. In the PACE Challenge, a typical graph size is several thousand vertices. In this scenario, billions of operations need to be performed at each vertex of the recursion tree. It turns out that it is simply impossible to solve the problem in the allotted time.
Let's try to optimize the solution. The minimum vertex section between a pair of vertices can be found by any algorithm constructing the maximum flow. You can let Dinits algorithm onto such a networkIn practice, it works very fast. I have a suspicion that theoretically it is possible to prove an estimate for the time of work
I tried several times to search for cuts between pairs of random vertices and take the most balanced one from them. Unfortunately, in the open PACE Challenge tests this gave poor results. I compared it with an algorithm that was scattered along the vertices of the maximum degree, starting them with a restriction on the depth of descent. After the algorithm trying to find the cut in this way, there remained larger graphs. This is due to the fact that the cuts turned out to be very unbalanced: after removing 5-10 peaks, only 15-20 were able to be split off.
It is worth noting that articles on theoretically the fastest algorithms use much more advanced techniques for selecting vertices for splitting. Such techniques have a very complex implementation and often poor grades of time and memory. I could not distinguish from them quite acceptable for practice.
How to apply simplification rules
We already have ideas for kernelization. Let me remind you:
- If there is an isolated vertex, delete it.
- If there is a vertex of degree 1, delete it and take its neighbor in response.
- If there is a vertex of degree at least k + 1 , take it in response.
With the first two everything is clear, with the third there is one trick. If in the comic bar problem we were given a restriction from above on k , then in the PACE Challenge you just need to find the vertex cover of the minimum size. This is a typical transformation of a Search Problem into a Decision Problem, often between the two types of tasks they do not make a difference. In practice, if we write a vertex coverage problem solver, there may be a difference. For example, as in the third paragraph.
In terms of implementation, there are two ways to do this. The first approach is called Iterative Deepening. It consists in the following: we can start with some reasonable restriction from below on the answer, and then run our algorithm, using this restriction as a restriction on the answer from above, without going down in recursion lower than this restriction. If we find some answer, it is guaranteed to be optimal, otherwise you can increase this limit by one and start again.
Another approach is to store some current optimal answer and look for a smaller answer, when found, change this parameter k to cut off excess branches in the search more.
After conducting some nightly experiments, I settled on a combination of these two methods: first, I run my algorithm with some kind of restriction on the search depth (choosing it so that it takes an insignificant time compared to the main solution) and use the best solution found as a restriction from above to the answer - that is, to that very k .
Vertices of degree 2
With vertices of degrees 0 and 1 we figured out. It turns out that this can also be done with vertices of degree 2, but for this, the graph will require more complex operations.
To explain this, you need to somehow identify the peaks. We call a vertex of degree 2 the vertex v , and its neighbors the vertices x and y . Then we will have two cases.
- When x and y are neighbors. Then you can take in response x and y , and delete v . Indeed, from this triangle at least two vertices must be taken in response and we certainly won’t lose if we take x and y : they probably have more neighbors, and v does not.
- When x and y are not neighbors. Then it is stated that all three vertices can be glued together into one. The idea is that in this case there is an optimal answer in which we take either v or both vertices x and y . Moreover, in the first case we have to take in response all the neighbors x and y , and in the second it is not necessary. This is exactly the case when we do not take the glued vertex in response and when we take it. It remains only to note that in both cases the response from such an operation decreases by one.

It is worth noting that such an approach for honest linear time is quite difficult to accurately implement. Gluing vertices is a difficult operation, you need to copy the lists of neighbors. If you do this carelessly, you can get asymptotically non-optimal operating time (for example, if you copy a lot of edges after each gluing). I settled on searching for whole paths from vertices of degree 2 and parsing a bunch of special cases, like loops from such vertices or from all such vertices except one.
In addition, it is necessary that this operation be reversible, so that during the return from recursion we restore the graph in its original form. To ensure this, I did not clear the lists of edges of the merged vertices, after which I just knew which edges should be directed to. This implementation of graphs also requires accuracy, but it provides honest linear time. And for graphs of several tens of thousands of edges, it completely fits into the processor cache, which gives great speed advantages.
Linear core
Finally, the most interesting part of the kernel.
First, recall that in bipartite graphs, the minimum vertex coverage can be sought for
The idea of a linear kernel is as follows: first we divide the graph, that is, instead of each vertex v, we get two vertices
We just learned to leave no more than 2k vertices in a graph . Indeed, if the remainder of the answer is at least half of all the vertices, then the total vertices there are no more than 2k .
Here I managed to take a small step forward. It is clear that the kernel constructed in this way depends on what kind of minimum vertex coverage in the bipartite graph we took. I would like to take such that the number of remaining vertices is minimal. Previously, they only knew how to do it in time.
Result
Practice shows that my solution works well on tests of several hundred vertices and several thousand edges. On such tests, it can be expected that a solution can be found in half an hour. The probability of finding an answer in an acceptable time period increases in principle if the graph has a lot of vertices of a large degree, for example, degrees 10 and above.
To participate in the competition, decisions had to be sent to optil.io . Judging by the plate presented there , my decision on open tests ranks third out of twenty with a wide margin from the second. To be completely honest, it’s not entirely clear how decisions will be evaluated at the competition itself: for example, my decision passes fewer tests than the decision in fourth place, but it works faster for those that pass.
Results on closed tests will be announced on July 1.
