Mathematics and the game "Set"
Whoever finds a “set” here will get a chocolate bar from me.
Set is a brilliant game in which we were cut about 5 years ago. Screaming, screaming, photographing combinations.
The rules of the game say that it was invented in 1991 by the geneticist Marsha Falco, making notes while researching epilepsy in German shepherds in 1974. For those whose brain is sufficiently exhausted by mathematics, after some time there is a suspicion that there are some echoes here with planimetry and drawing straight lines through the points. (For given two cards, there is one and only one card that goes with them in the same set.)

Marsha Falco asks: “Well, didn’t find the“ set “?”
Remember the rules
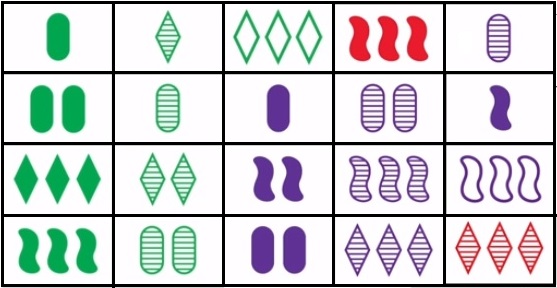
Seth is a card game. All cards have four parameters, each of which takes three values (total 3 x 3 × 3 × 3 = 81 cards).

The types and values of the parameters are as follows:
- figure :: = ellipse | rhombus | "Snot"
- color :: = red | green | purple
- fill :: = white | striped | solid
- number :: = 1 | 2 | 3
The goal of the game is to find special combinations of three cards. Three cards are called a “set” if for each of the four attributes of the card either all are the same or all are different.
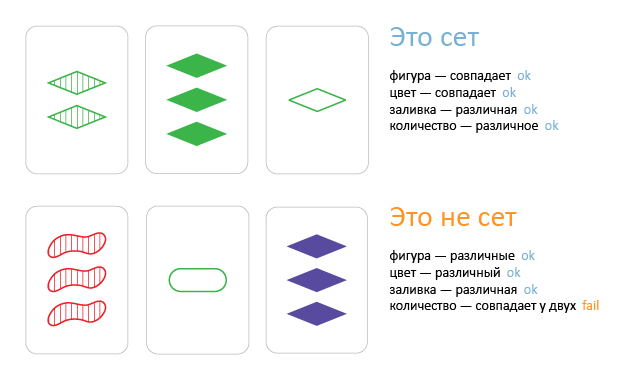
In other words, we can say that three cards will not make a set if two cards have one parameter value and the third one is different. You can see that for any two cards there will always be a third (and only one) with which they will be a set.
Game progress: the leader puts 12 cards on the table. When someone finds a set, he shouts “Set!” And then calmly picks up the components of the set card. If there is no set in the laid out cards (most of all, it just seems that there isn’t), the host puts out three more cards.
The maximum number of cards without a set is 20. The round continues until the deck runs out. The one who collected more sets wins.
Mathematicians fussed and presented a combination of 20 cards. Who considers himself Chuck Norris, can forget this picture and try to collect “solitaire” without a set yourself.
Or check, what if there is still a “set”?
20 cards without set
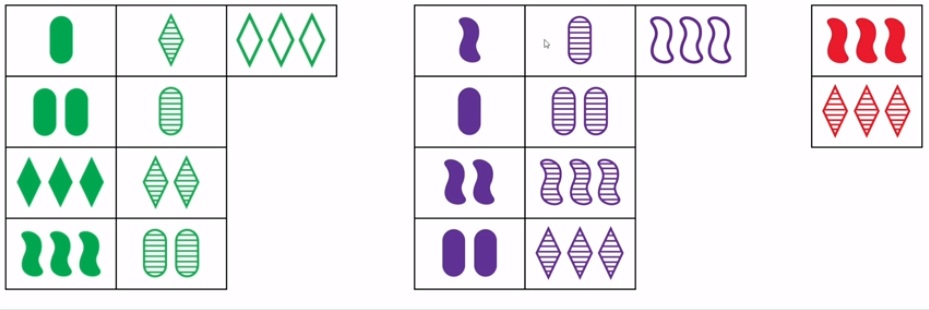
It is convenient to verify that there is no “color set”.
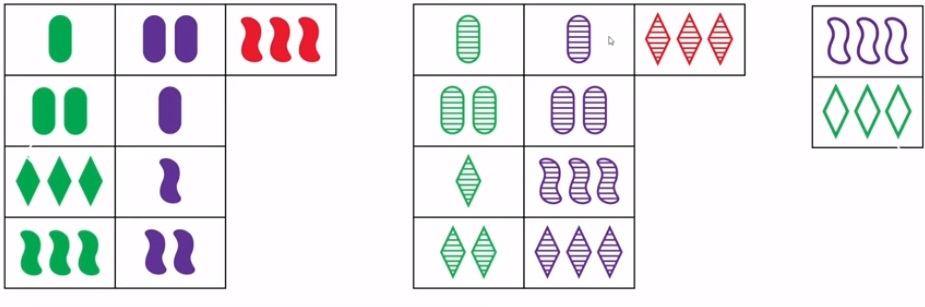
The same cards, but the location shows that he carried sets by the "fill" parameter.
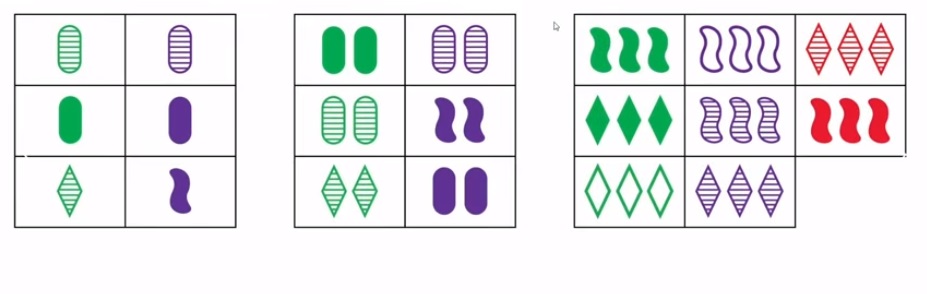
In count.
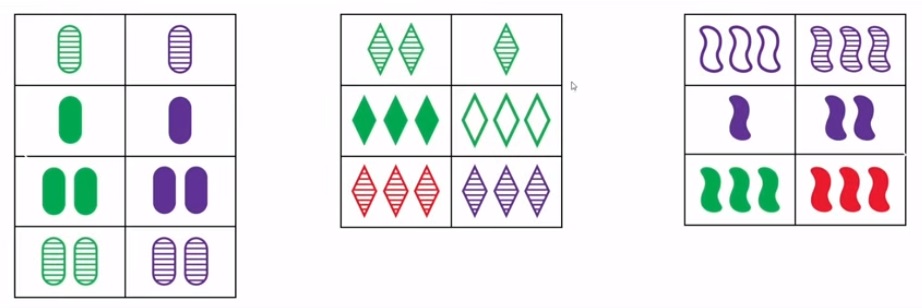
According to the figures.
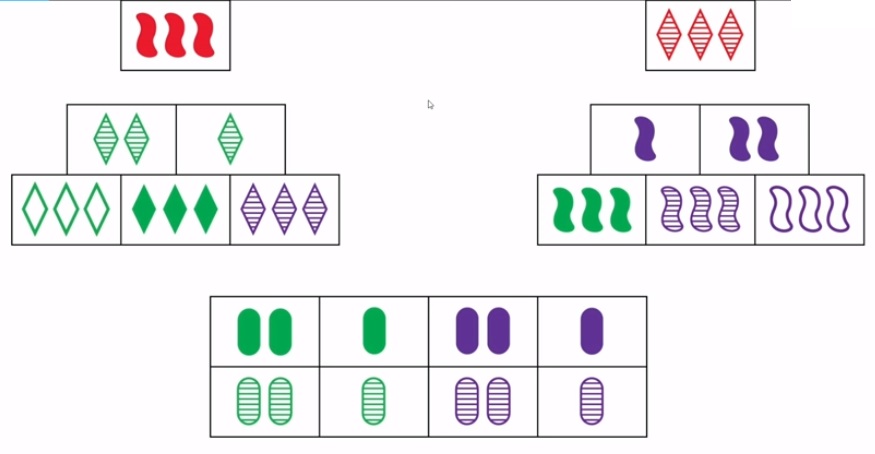
There is no set on the difference of signs.
An open unsolved math problem
How many cards can I put out to prevent a single “set”? The sign has three meanings.
with 1 "sign" - 2 cards
2 signs - 4 cards
3 signs - 9 cards
4 signs - 20 cards
5 signs - 45 cards
6 signs - 112 cards
7 signs - xs
And with "n → ∞"?
Video
Game creator:
Alexey Savvateev sparkles about Seth:
