CortexM3 / M4 (ARM) hardware bit banding, kernel architecture, assembler, C / C ++ 14 and a drop of metaprogramming
Introduction
Attention, this is not another “Hello world” article on how to blink an LED or get into its first interrupt on STM32. However, I tried to give comprehensive explanations on all the issues raised, so the article will be useful not only to many professional and dreaming of becoming such developers (as I hope), but also to novice microcontroller programmers, as this topic for some reason gets around on countless sites / blogs "MK programming teachers."
Why did I decide to write this?
Although I exaggerated, having said earlier that the hardware bit banding of the Cortex-M family is not described on specialized resources, there are still places where this feature is covered (and even met one article here), but this topic clearly needs to be supplemented and modernized. I note that this also applies to English-language resources. In the next section, I will explain why this kernel feature can be extremely important.
Theory
(and those who are familiar with it can jump right into practice)
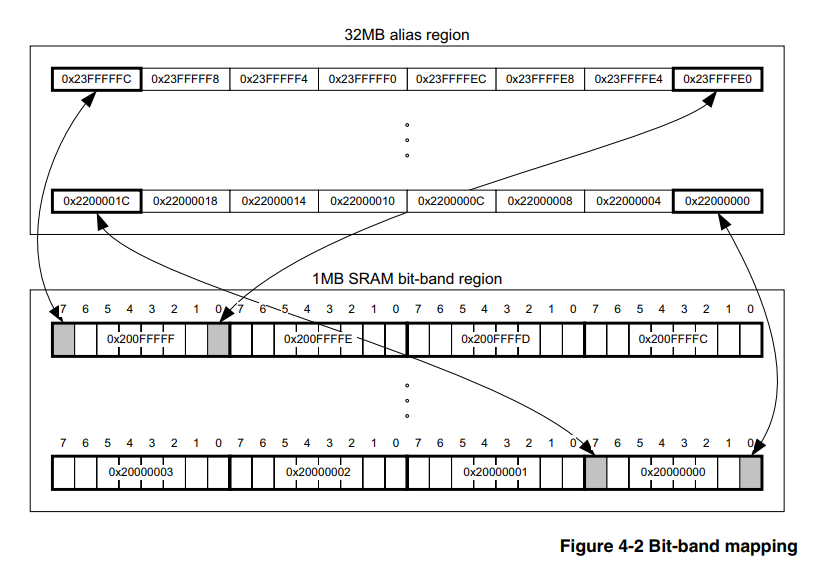
Hardware bit banding is a feature of the core itself, therefore it does not depend on the family and company of the microcontroller manufacturer, the main thing is that the core is suitable. In our case, let it be Cortex-M3. Therefore, information on this issue should be sought in an official document on the core itself, and there is such a document, here it is , section 4.2 describes in detail how to use this tool.
Here I would like to make a small technical digression for programmers who are not familiar with assembler, of whom the majority are now, due to the propagandized complexity and uselessness of assembler for such “serious” 32bit microcontrollers as STM32, LPC, etc. Moreover, one can often encounter attempts censure for the use of assembler in this area, even on the Habr. In this section I want to briefly describe the mechanism of writing to MK memory, which should clarify the advantages of bit banding.
I will explain a specific simple example for most STM32. Suppose I need to turn PB0 into a general-purpose output. A typical solution would look like this:
GPIOB->MODER |= GPIO_MODER_MODER0_0;Obviously, we use the bitwise “OR” in order not to overwrite the remaining bits of the register.
For the compiler, this translates to the following set of 4 instructions:
- Download GPIOB-> MODER to the general purpose register (RON)
- Upload the values to the other RON at the address indicated in the RON from p1.
- Make a bitwise OR of this value with GPIO_MODER_MODER0_0.
- Download the result back to GPIOB-> MODER.
Also, one should not forget that this kernel uses the thumb2 instruction set, which means that they can be different in volume. I also note that everywhere we are talking about the level of optimization O3.
In assembly language, it looks like this:

It can be seen that the very first instruction is nothing more than a pseudo-instruction with an offset, we find at the PC address (given the conveyor belt) + 0x58 the value of the register address.
It turns out we have 4 steps (and more clock cycles) and 14 bytes of occupied memory per operation.
If you want to know more about this, then I recommend the book [2], by the way, there is also in Russian.
We pass to the bit_banding method.
The essence, according to the peasant, is that the processor has a specially allocated memory area, writing the values into which we do not change other bits of the peripheral register or RAM. That is, we do not need to fulfill points 2) and 3) described above, and for this it is enough to only recount the address according to the formulas from [1].

We are trying to do a similar operation, its assembler:

Recalculated address:

Here we have added the write instruction # 1 to the RON, but anyway, the result is 10 bytes, instead of 14, and a couple of clock cycles less.
But what if the difference is ridiculous?
On the one hand, the savings are not significant, especially in cycles when it’s already a habit of overclocking the controller to 168 MHz. In an average project, the moments where you can apply this method will be 40 - 80, respectively, in bytes the savings can reach 250 bytes if the addresses differ. And when you consider that "zashkvarom" is now considered system device programming directly on the registers, and "cool" to use any cubes
Also, the figure of 250 bytes is distorted by the fact that high-level libraries are actively used in the community, firmware inflate to indecent sizes. When programming at a low level, this is at least 2 - 5% of the software volume for an average project, with competent architecture and O3 optimization.
Again, I do not want to say that this is some kind of super-duper-mega cool tool that every self-respecting MK programmer should use. But if I can cut costs even by such a small part, then why not?
Implementation
All options will be given only to configure the peripherals, since I did not come across a situation where it would be necessary for RAM. Strictly speaking, for RAM, the formula is similar, just change the base addresses for calculation. So how do you implement this?
Assembler
Let's go from the bottom, from my beloved Assembler.
On assembler projects, I usually allocate a couple of 2-byte (according to the instructions that work with them) RON under # 0 and # 1 for the whole project, and use them also in macros, which reduces me another 2 bytes on an ongoing basis. Remark, I did not find CMSIS in Assembler for STM, because I put the bit number in the macro right away, and not its register value.
Implementation for GNU Assembler
@Захардкориваю два РОНа.
MOVW R0, 0x0000
MOVW R1, 0x0001
@Макрос установки бита
.macro PeriphBitSet PerReg, BitNum
LDR R3, =(BIT_BAND_ALIAS+(((\PerReg) - BIT_BAND_REGION) * 32) + ((\BitNum) * 4))
STR R1, [R3]
.endm
@Макрос сброса бита
.macro PeriphBitReset PerReg, BitNum
LDR R3, =(BIT_BAND_ALIAS+((\PerReg - BIT_BAND_REGION) * 32) + (\BitNum * 4))
STR R0, [R3]
.endmExamples:
Assembler Examples
PeriphSet TIM2_CCR2, 0
PeriphBitReset USART1_SR, 5
The undoubted advantage of this option is that we have full control, which cannot be said about further options. And as the last section of the article will show, plus this one is very significant.
However, no one needs projects for MK in Assembler, from about the end of the zero, which means you need to switch to SI.
Plain c
Honestly, a simple Sishny option was found by me at the beginning of the path, somewhere in the vast network. At that time, I already implemented bit banding in Assembler, and accidentally stumbled upon a C file, it immediately worked and I decided not to invent anything.
Implementation for plain C
/*!<=================PLAIN C SECTION========================>!*/
#define MASK_TO_BIT31(A) (A==0x80000000)? 31 : 0
#define MASK_TO_BIT30(A) (A==0x40000000)? 30 : MASK_TO_BIT31(A)
#define MASK_TO_BIT29(A) (A==0x20000000)? 29 : MASK_TO_BIT30(A)
#define MASK_TO_BIT28(A) (A==0x10000000)? 28 : MASK_TO_BIT29(A)
#define MASK_TO_BIT27(A) (A==0x08000000)? 27 : MASK_TO_BIT28(A)
#define MASK_TO_BIT26(A) (A==0x04000000)? 26 : MASK_TO_BIT27(A)
#define MASK_TO_BIT25(A) (A==0x02000000)? 25 : MASK_TO_BIT26(A)
#define MASK_TO_BIT24(A) (A==0x01000000)? 24 : MASK_TO_BIT25(A)
#define MASK_TO_BIT23(A) (A==0x00800000)? 23 : MASK_TO_BIT24(A)
#define MASK_TO_BIT22(A) (A==0x00400000)? 22 : MASK_TO_BIT23(A)
#define MASK_TO_BIT21(A) (A==0x00200000)? 21 : MASK_TO_BIT22(A)
#define MASK_TO_BIT20(A) (A==0x00100000)? 20 : MASK_TO_BIT21(A)
#define MASK_TO_BIT19(A) (A==0x00080000)? 19 : MASK_TO_BIT20(A)
#define MASK_TO_BIT18(A) (A==0x00040000)? 18 : MASK_TO_BIT19(A)
#define MASK_TO_BIT17(A) (A==0x00020000)? 17 : MASK_TO_BIT18(A)
#define MASK_TO_BIT16(A) (A==0x00010000)? 16 : MASK_TO_BIT17(A)
#define MASK_TO_BIT15(A) (A==0x00008000)? 15 : MASK_TO_BIT16(A)
#define MASK_TO_BIT14(A) (A==0x00004000)? 14 : MASK_TO_BIT15(A)
#define MASK_TO_BIT13(A) (A==0x00002000)? 13 : MASK_TO_BIT14(A)
#define MASK_TO_BIT12(A) (A==0x00001000)? 12 : MASK_TO_BIT13(A)
#define MASK_TO_BIT11(A) (A==0x00000800)? 11 : MASK_TO_BIT12(A)
#define MASK_TO_BIT10(A) (A==0x00000400)? 10 : MASK_TO_BIT11(A)
#define MASK_TO_BIT09(A) (A==0x00000200)? 9 : MASK_TO_BIT10(A)
#define MASK_TO_BIT08(A) (A==0x00000100)? 8 : MASK_TO_BIT09(A)
#define MASK_TO_BIT07(A) (A==0x00000080)? 7 : MASK_TO_BIT08(A)
#define MASK_TO_BIT06(A) (A==0x00000040)? 6 : MASK_TO_BIT07(A)
#define MASK_TO_BIT05(A) (A==0x00000020)? 5 : MASK_TO_BIT06(A)
#define MASK_TO_BIT04(A) (A==0x00000010)? 4 : MASK_TO_BIT05(A)
#define MASK_TO_BIT03(A) (A==0x00000008)? 3 : MASK_TO_BIT04(A)
#define MASK_TO_BIT02(A) (A==0x00000004)? 2 : MASK_TO_BIT03(A)
#define MASK_TO_BIT01(A) (A==0x00000002)? 1 : MASK_TO_BIT02(A)
#define MASK_TO_BIT(A) (A==0x00000001)? 0 : MASK_TO_BIT01(A)
#define BIT_BAND_PER(reg, reg_val) (*(volatile uint32_t*)(PERIPH_BB_BASE+32*((uint32_t)(&(reg))-PERIPH_BASE)+4*((uint32_t)(MASK_TO_BIT(reg_val)))))
As you can see, a very simple and straightforward piece of code written in the language of the processor. The main work here is the translation of CMSIS values into a bit number, which was absent as a need for an assembler version.
Oh yes, use this option like this:
Examples for plain C
BIT_BAND_PER(GPIOB->MODER, GPIO_MODER_MODER0_0) = 0; //Сброс
BIT_BAND_PER(GPIOB->MODER, GPIO_MODER_MODER0_0) = 1; //Установка (!0)
However, modern (massively, according to my observations, approximately from 2015) trends are in favor of replacing C with C ++ even for MK. And macros are not the most reliable tool, so the next version was destined to be born.
Cpp03
Here, a very interesting and discussed, but little used in view of its complexity, with one hackneyed example of a factorial comes up, the tool is metaprogramming.
After all, the task of translating the value of a variable into a bit number is ideal (there are already values in CMSIS), and in this case it is practical for compile time.
I implemented this as follows using templates:
Implementation for C ++ 03
template struct bit_num_from_value
{
enum { bit_num = (val == comp_val) ? cur_bit_num : bit_num_from_value::bit_num };
};
template struct bit_num_from_value(0x80000000), static_cast(31)>
{
enum { bit_num = 31 };
};
#define BIT_BAND_PER(reg, reg_val) *(reinterpret_cast(PERIPH_BB_BASE + 32 * (reinterpret_cast(&(reg)) - PERIPH_BASE) + 4 * (bit_num_from_value(reg_val), static_cast(0x01), static_cast(0)>::bit_num)))
You can use it in the same way:
Examples for C ++ 03
BIT_BAND_PER(GPIOB->MODER, GPIO_MODER_MODER0_0) = false; //Сброс
BIT_BAND_PER(GPIOB->MODER, GPIO_MODER_MODER0_0) = true; //Установка
And why was the macro left? The fact is that I don’t know of another way to guaranteedly insert this operation without going to another area of the program code. I would be very glad if they prompted me in the comments. Neither templates nor inline functions provide such a guarantee. Yes, and the macro here copes with its task perfectly well, there is no point in changing it just because the
Surprisingly, time still did not stand still, compilers more and more actively supported C ++ 14 / C ++ 17, why not take advantage of the innovations, making the code more understandable.
Cpp14 / cpp17
Implementation for C ++ 14
constexpr uint32_t bit_num_from_value_cpp14(uint32_t val, uint32_t comp_val, uint32_t bit_num)
{
return bit_num = (val == comp_val) ? bit_num : bit_num_from_value_cpp14(val, 2 * comp_val, bit_num + 1);
}
#define BIT_BAND_PER(reg, reg_val) *(reinterpret_cast(PERIPH_BB_BASE + 32 * (reinterpret_cast(&(reg)) - PERIPH_BASE) + 4 * (bit_num_from_value_cpp14(static_cast(reg_val), static_cast(0x01), static_cast(0)))))
As you can see, I just replaced the templates with a recursive constexpr function, which, in my opinion, is more clear to the human eye.
Use the same way. By the way, in C ++ 17, in theory, you can use the recursive lambda constexpr function, but I'm not sure that this will lead to at least some simplifications, and also will not complicate the assembler order.
In summary, all three C / Cpp implementations give an equally correct set of instructions, according to the Theory section. I have been working with all implementations on IAR ARM 8.30 and gcc 7.2.0 for a long time.
Practice is a bitch
That's all, it seems, happened. The memory savings were calculated, the implementation chosen, ready to improve performance. Not here, it was just a case of a divergence of theory and practice. And when was it different?
I would never have published it if I hadn’t tested it, but how much realistically the occupied volume is reduced on projects. I specifically on a couple of old projects replaced this macro with a regular implementation without a mask, and looked at the difference. The result surprised unpleasantly.
As it turned out, the volume remains virtually unchanged. I specifically chose projects where exactly 40-50 such instructions were used. According to the theory, I had to save well at least 100 bytes, and at most 200. In practice, the difference turned out to be 24 - 32 bytes. But why?
Usually, when you set up peripherals, you set up 5-10 registers almost in a row. And at a high level of optimization, the compiler does not arrange the instructions exactly in the order of the registers, but arranges the instructions as it seems correct, sometimes interfering with them in seemingly inextricable places.
I see two options (here are my speculations):
- Or the compiler is so smart that it knows for you how it will be better to optimize the set of instructions
- Or the compiler is still not smarter than a person, and confuses himself when he encounters such constructions
That is, it turns out that this method in “high-level” languages at a high level of optimization only works correctly if there are no similar operations in proximity to one such operation.
Incidentally, at the O0 level, theory and practice converge in any case, but I am not interested in this level of optimization.
I summarize
A negative result is also a result. I think everyone will draw conclusions for himself. Personally, I will continue to use this technique, it certainly will not be worse from it.
I hope it was interesting and I want to express a huge respect to those who have read to the end.
List of literature
- "Cortex-M3 Technical Reference Manual", Section 4.2, ARM 2005.
- The definitive guide to the ARM Cortex-M3, Joseph Yiu.
PS I have in my bag a little coverage of topics related to the development of embedded electronics. Let me know, if interested, I will slowly get them.
PPS Somehow it turned out crookedly to insert sections of the code, please tell me how to improve, if possible. In general, you can copy a piece of code of interest to notepad and avoid unpleasant emotions in the analysis.
