Creating a procedural puzzle generator
- Transfer
This post describes the level generator for my Linjat puzzle game . A post can be read without preparation, but it is easier to assimilate if you play in several levels. I posted the source code on github ; all discussed in the article is in the file
Sample post plan:
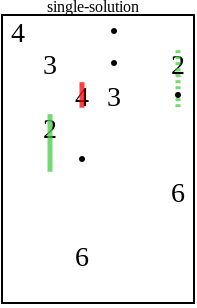
To understand how the level generator works, you need, unfortunately, to understand the rules of the game. Fortunately, they are very simple. The puzzle consists of a grid containing empty squares, numbers and dots. Example:

The goal of the player is to draw a vertical or horizontal line through each of the numbers, subject to three conditions:
Example solution:
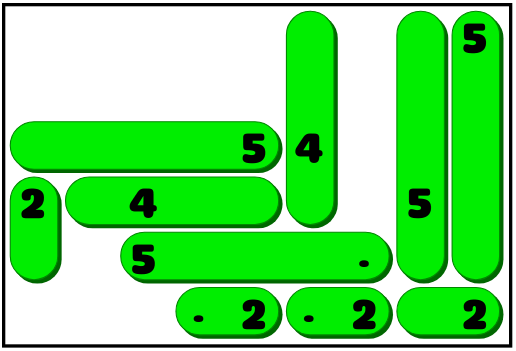
Hurrah! The game design is ready, the UI is implemented, and now the only thing left is to find several hundred good puzzles. And for such games it usually does not make sense to try to create such puzzles manually. This is a computer job.
What makes the puzzle for this game good? I am inclined to believe that puzzle games can be divided into two categories. There are games in which you explore a complex state space from beginning to end (for example, Sokoban or Rush Hour ), and in which it may not be obvious what states exist in the game. And there are games in which all states are known from the very beginning, and we gradually fashion the state space using the process of eliminating unnecessary ones (for example, Sudoku or Picross ). My game definitely falls into the second category.
Players have very different requirements for these different types of puzzles. In the second case, they expect that the puzzle can only be solved by deduction, and that they will never need to go back / guess / trial and error [0] [1] .
It is not enough to know whether a puzzle can only be solved by logic. In addition, we need to somehow understand how good the created puzzles are. Otherwise, most levels will be just trivial slag. In an ideal situation, this principle could also be used to create a smooth progress curve, so that as the player progresses through the game, the levels gradually become more difficult.
The first step to meeting these requirements is to create a game solver optimized for this purpose. The backtracking solver allows you to quickly and accurately determine whether the puzzle is solvable; in addition, it can be modified to determine whether the solution is unique. But he cannot give an idea of how complicated the puzzle really is, because people solve them differently. Solver must imitate human behavior.
How does a person solve this puzzle? Here are a couple of obvious moves that the in-game tutorial teaches:
Similar reasoning is the very basis of the game. The player looks for ways to stretch a little one line, and then examines the field again, because it can give him information to make another logical conclusion. Creating a solver that follows these rules will be enough to determine if a person can solve the puzzle without going back.
However, this does not tell us anything about the complexity or interestingness of the level. Besides solvability, we somehow need to quantify complexity.
An obvious first idea for the rating function: the more moves you need to solve the puzzle, the harder it is. This is probably a good metric in other games, but mine, most likely, is more important than the number of allowed moves that a player has. If a player can make 10 logical conclusions, then he will most likely find one of them very quickly. If there is only one right move, it will take more time.
That is, as a first approximation, we need the decision tree to be deep and narrow: there is a long dependence of moves from beginning to end, and at each moment of time there are only a small number of ways to move up the chain [2] .
How do we determine the width and depth of a tree? A single solution to the puzzle and evaluation of the created tree will not give an exact answer. The exact order in which moves are made affects the shape of the tree. We need to consider all possible solutions and do with them something like optimization for the best and worst cases. I am familiar with the technique of rough search of search graphs in puzzle games , but for this project I wanted to create a one-pass solver, and not some exhaustive search. Due to the optimization phase, I tried to ensure that the runtime of the solver was measured not in seconds, but in milliseconds.
I decided not to. Instead, my solver does not actually make one move at a time, but solves the puzzle in layers: taking a state, he finds all the valid moves that can be made. Then he applies all these moves at the same time and starts anew in a new state. The number of layers and the maximum number of moves found on one layer are then used as approximate values of the depth and width of the search tree as a whole.
Here's how to solve one of the difficult puzzles with this model. Dotted lines are lines stretched on this layer of the solver, solid lines are those that have not changed. The green lines are the correct length, the red ones are not yet complete.

The next problem is that all the moves made by the player are created equal. What we listed at the beginning of this section is just common sense. Here is an example of a more complex deduction rule, the search for which will require a little more thought. Consider the following field:

The points in C and D can be covered only by the five and the middle four (and not a single number can cover both points at the same time). This means that the four in the middle should cover one point of two, and therefore cannot be used to cover A. Therefore, the point A should close the four in the lower left corner.
Obviously, it would be foolish to consider this chain of reasoning equal to the simple conclusion "this point can only be reached from this number." Is it possible to give more weight to these more complex rules in the evaluation function? Unfortunately, in a layer-based solver, this is not possible, because it is not guaranteed to find a solution at the lowest cost. This is not only a theoretical problem - in practice it often happens that part of the field can be solved either by a single complex argument, or by a chain of much simpler moves. In fact, a layer-based solver finds the shortest, and not the least costly path, and this cannot be reflected in the evaluation function.
As a result, I came to this decision: I changed the solver so that each layer consisted of only one type of reasoning. The algorithm bypasses the rules of reasoning in an approximate order of complexity. If the rule finds some moves, then they are applied, and the iteration ends, and the next iteration starts the list from the very beginning.
Then the decision is assigned an assessment: each layer is assigned costs based on one rule that was used in it. This still does not guarantee that the solution will be the most low-cost, but if the weights are selected correctly, the algorithm will at least not find a costly solution if there is a cheap one.
Moreover, it is very much like the way people solve puzzles. They first try to find easy solutions, and begin to actively move their brains only if there are no simple moves.
The previous section determined whether a particular level was good or bad. But just this is not enough, we still need to somehow generate levels so that the solver can evaluate them. It is very unlikely that a randomly generated world will be solvable, not to mention interesting.
The main idea (it is by no means new) is the alternate use of the solver and generator. Let's start with a puzzle, which is probably unsolvable: just place two to five numbers in random squares of the cell:

Solver works until it can develop further:
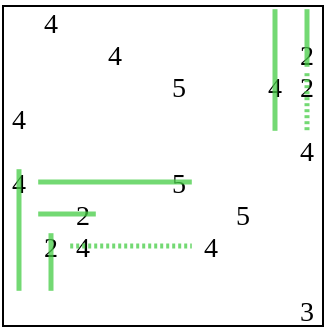
Then the generator adds more information to the puzzle in the form of a point, after which the execution of the solver continues.
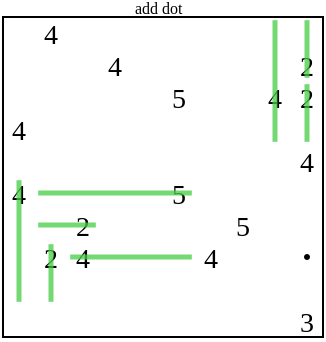
In this case, the added point to the solver is not enough for further development. Then the generator will continue to add new points until it satisfies the solver:

And then the solver continues his usual work:

This process continues either until the puzzle is solved, or until there is more information left to add (for example, when each cell that can be reached from the number already contains a point).
This method only works if the added new information cannot make any of the conclusions made earlier incorrect. This would be difficult to do when adding numbers to the grid [3] . But adding new points to the field has this property; at least for the reasoning rules that I use in this program.
Where should the algorithm add points? In the end, I decided to add them to the empty space, which can be closed in the initial state with as many lines as possible, so that each point seeks to give out as little information as possible. I did not try to specifically place the point in the place where it would be useful for advancement in solving the puzzle at the moment when the solver gets stuck. This creates a very convenient effect: most of the points at the beginning of the puzzle seem completely useless, which makes the puzzle more difficult than it really is. If all this is a lot of obvious moves that a player can make, but for some reason not one of them does not work properly. As a result, it turned out that the puzzle generator behaves a bit like a pig.
This process does not always create a solution, but it is quite fast (about 50-100 milliseconds), so to generate a level, you can simply repeat it several times. Unfortunately, he usually creates mediocre puzzles. From the very beginning there are too many obvious moves, the field fills up very quickly and the decision tree turns out to be rather shallow.
The process described above created mediocre puzzles. At the last stage, I use these levels as the basis for the optimization process. It works as follows.
The optimizer creates a pool that contains up to 10 puzzle options. The pool is initialized with a new generated random puzzle. At each iteration, the optimizer selects one puzzle from the pool and performs its mutation.
The mutation deletes all points, and then slightly changes the numbers (i.e. decreases / increases the value of a randomly selected number or moves the number to another cell in the grid). You can apply several mutations to the field at the same time. Then we run the solver in the special level generation mode described in the previous section. He adds enough points to the puzzle so that it becomes solvable again.
After that, we start the solver again, this time in normal mode. During this run, the solver monitors a) the depth of the decision tree, b) the frequency of the need for different types of rules, c) the width of the decision tree at different points in time. The puzzle is evaluated based on the criteria described above. The evaluation function prefers deep and narrow solutions, and levels of increased complexity also add more weight to puzzles in which more complex rules of reasoning are required.
Then a new puzzle is added to the pool. If the pool contains more than 10 puzzles, then the worst is discarded.
This process is repeated several times (approximately 10,000-50000 iterations took me). After that, the highest rated version of the puzzle is saved to the puzzle level database. Here's what the progress of the best puzzle in one optimization run looks like:

I tried using other ways to structure optimization. In one version, simulated annealing was used; others were genetic algorithms with various crossing-over operations. None of the solutions performed as well as a naive algorithm with a pool of options going back to the top.
When a puzzle has a unique unique solution, an interesting difficulty arises. Is it possible to allow the player to assume that there is one solution and draw conclusions based on this? Would it be fair if the puzzle generator suggested that the player did so?
In a post on HackerNews, I said that there are four options for approaching this situation:
Initially, I chose the latter option, and that was a terrible mistake. It turned out that I took into account only one way in which the uniqueness of the solution led to information leakage, and it is actually quite rare. But there are others; one of them was in fact present at every level I generated and often led to the fact that the solution became trivial. Therefore, in May 2019, I changed the Hard and Expert modes using the third option.
The most annoying case is a deuce with a dashed line in this field:
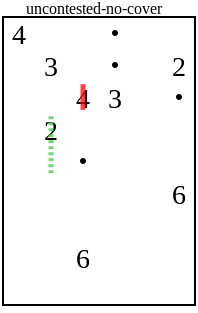
Why can a cunning player make such a conclusion? A deuce can cover any of the four neighboring squares. None of them have dots, so they do not have to be covered by a line. And the square below does not have overlays with any other numbers. If there is a single solution, then this should be the case when other numbers cover the remaining three squares, and the two closes the square under it.
The solution is to add a few more points when recognizing such cases:

Another common case is a dash with a dotted line in this field:
The squares to the left and top of the two are no different. None of them have a point, and not one can be reached from any other number. Any solution in which a deuce covers the top square will have a corresponding solution in which it closes the left square, and vice versa. If there was a single unique solution, then this could not be, and the deuce should have covered the bottom square.
I decided this type of case in the way "if it hurts, then don’t touch it." Solver applied this rule at an early stage in the list of priorities and assigned such negative weight to such moves. Puzzles with this feature are usually discarded by the optimizer, and the few remaining are discarded at the stage of the final selection of levels for the published game.
This is not a complete list. During play testing with a deliberate search for errors, I found many other rules for unique solutions. But most of them seemed rare and they were enough to find, so they did not greatly simplify the game. If someone solves the puzzle using such reasoning, then I will not blame it on them.
Initially, the game was developed as an experiment in the procedural generation of puzzles. The game’s design and generator went hand in hand, so the techniques themselves are difficult to apply directly to other games.
The question to which I have no answer: has the investment of such efforts in procedural generation justified itself? Player feedback on level design was very controversial. In positive comments, it was usually said that some tricky trick is always felt in puzzles. In most negative reviews, they wrote to me that the game lacks a gradient of complexity.
I still have a couple of puzzles in their infancy, and I liked the generator so much that I most likely use a similar procedural approach for them. I’ll change only one thing: from the very beginning I will conduct active playtesting with the search for errors.
[0] Or, at least, it seemed to me. But when I watched the players live, almost half of them just made guesses, and then iterated through them. Anyway.
[1] Readers of my article should also read the article Solving Minesweeper and making it better Magnus Hoff.
[2] I’ll clarify that the depth / narrowness of a tree is a metric that I considered significant for my game, and not for all other puzzles. For example, there is a good argument that the Rush Hour puzzle is interesting if it has several ways to solve almost, but not exactly the same length. But it happened because Rush Hour is a game to find the shortest solution, and not just any solution.
[3] Excluding the addition of units. There were no dots in the first version of the puzzle, and the plan was for the generator to add units if necessary. But that seemed too restrictive.
src/main.cc. Sample post plan:
- Linjat is a logic game in which you need to close all numbers and points in the grid with lines.
- The puzzles are procedurally generated using a combination of solver, generator and optimizer.
- Solver tries to solve the puzzles the way a person would do, and assigns each puzzle a rating of interest.
- The puzzle generator is designed in such a way that it is possible to easily change one part of the puzzle (number), while all other parts (points) are changed so that the puzzle remains solvable.
- The puzzle optimizer repeatedly solves the levels and generates new variations from the most interesting ones found at the moment.
rules
To understand how the level generator works, you need, unfortunately, to understand the rules of the game. Fortunately, they are very simple. The puzzle consists of a grid containing empty squares, numbers and dots. Example:

The goal of the player is to draw a vertical or horizontal line through each of the numbers, subject to three conditions:
- A line through a number must be the same length as the number.
- Lines cannot intersect.
- All points must be closed with lines.
Example solution:

Hurrah! The game design is ready, the UI is implemented, and now the only thing left is to find several hundred good puzzles. And for such games it usually does not make sense to try to create such puzzles manually. This is a computer job.
Requirements
What makes the puzzle for this game good? I am inclined to believe that puzzle games can be divided into two categories. There are games in which you explore a complex state space from beginning to end (for example, Sokoban or Rush Hour ), and in which it may not be obvious what states exist in the game. And there are games in which all states are known from the very beginning, and we gradually fashion the state space using the process of eliminating unnecessary ones (for example, Sudoku or Picross ). My game definitely falls into the second category.
Players have very different requirements for these different types of puzzles. In the second case, they expect that the puzzle can only be solved by deduction, and that they will never need to go back / guess / trial and error [0] [1] .
It is not enough to know whether a puzzle can only be solved by logic. In addition, we need to somehow understand how good the created puzzles are. Otherwise, most levels will be just trivial slag. In an ideal situation, this principle could also be used to create a smooth progress curve, so that as the player progresses through the game, the levels gradually become more difficult.
Solver
The first step to meeting these requirements is to create a game solver optimized for this purpose. The backtracking solver allows you to quickly and accurately determine whether the puzzle is solvable; in addition, it can be modified to determine whether the solution is unique. But he cannot give an idea of how complicated the puzzle really is, because people solve them differently. Solver must imitate human behavior.
How does a person solve this puzzle? Here are a couple of obvious moves that the in-game tutorial teaches:
- If a point can be reached from only one number, then to close a point you need to draw a line from that number. In this example, the point can be reached only from the three, but not from the four:
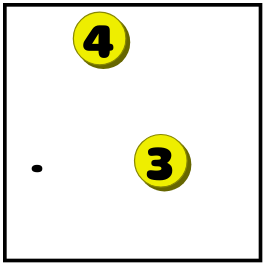
And this leads to this situation:
- If the line does not fit in one direction, then it must be placed in another. In the above example, the four can no longer be positioned vertically, so we know that it will be horizontal:
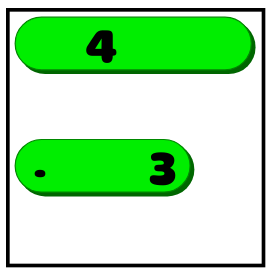
- If it is known that the line of length X must be in a certain position (vertical / horizontal) and there is not enough empty space to place a line of X empty cells on both sides, then you need to cover several squares in the middle. If the four were three in the example shown above, then we would not know whether it stretches all the way to the right or left. But we would know that the line should cover two middle squares:
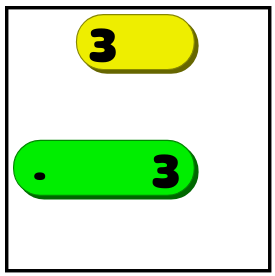
Similar reasoning is the very basis of the game. The player looks for ways to stretch a little one line, and then examines the field again, because it can give him information to make another logical conclusion. Creating a solver that follows these rules will be enough to determine if a person can solve the puzzle without going back.
However, this does not tell us anything about the complexity or interestingness of the level. Besides solvability, we somehow need to quantify complexity.
An obvious first idea for the rating function: the more moves you need to solve the puzzle, the harder it is. This is probably a good metric in other games, but mine, most likely, is more important than the number of allowed moves that a player has. If a player can make 10 logical conclusions, then he will most likely find one of them very quickly. If there is only one right move, it will take more time.
That is, as a first approximation, we need the decision tree to be deep and narrow: there is a long dependence of moves from beginning to end, and at each moment of time there are only a small number of ways to move up the chain [2] .
How do we determine the width and depth of a tree? A single solution to the puzzle and evaluation of the created tree will not give an exact answer. The exact order in which moves are made affects the shape of the tree. We need to consider all possible solutions and do with them something like optimization for the best and worst cases. I am familiar with the technique of rough search of search graphs in puzzle games , but for this project I wanted to create a one-pass solver, and not some exhaustive search. Due to the optimization phase, I tried to ensure that the runtime of the solver was measured not in seconds, but in milliseconds.
I decided not to. Instead, my solver does not actually make one move at a time, but solves the puzzle in layers: taking a state, he finds all the valid moves that can be made. Then he applies all these moves at the same time and starts anew in a new state. The number of layers and the maximum number of moves found on one layer are then used as approximate values of the depth and width of the search tree as a whole.
Here's how to solve one of the difficult puzzles with this model. Dotted lines are lines stretched on this layer of the solver, solid lines are those that have not changed. The green lines are the correct length, the red ones are not yet complete.

The next problem is that all the moves made by the player are created equal. What we listed at the beginning of this section is just common sense. Here is an example of a more complex deduction rule, the search for which will require a little more thought. Consider the following field:

The points in C and D can be covered only by the five and the middle four (and not a single number can cover both points at the same time). This means that the four in the middle should cover one point of two, and therefore cannot be used to cover A. Therefore, the point A should close the four in the lower left corner.
Obviously, it would be foolish to consider this chain of reasoning equal to the simple conclusion "this point can only be reached from this number." Is it possible to give more weight to these more complex rules in the evaluation function? Unfortunately, in a layer-based solver, this is not possible, because it is not guaranteed to find a solution at the lowest cost. This is not only a theoretical problem - in practice it often happens that part of the field can be solved either by a single complex argument, or by a chain of much simpler moves. In fact, a layer-based solver finds the shortest, and not the least costly path, and this cannot be reflected in the evaluation function.
As a result, I came to this decision: I changed the solver so that each layer consisted of only one type of reasoning. The algorithm bypasses the rules of reasoning in an approximate order of complexity. If the rule finds some moves, then they are applied, and the iteration ends, and the next iteration starts the list from the very beginning.
Then the decision is assigned an assessment: each layer is assigned costs based on one rule that was used in it. This still does not guarantee that the solution will be the most low-cost, but if the weights are selected correctly, the algorithm will at least not find a costly solution if there is a cheap one.
Moreover, it is very much like the way people solve puzzles. They first try to find easy solutions, and begin to actively move their brains only if there are no simple moves.
Generator
The previous section determined whether a particular level was good or bad. But just this is not enough, we still need to somehow generate levels so that the solver can evaluate them. It is very unlikely that a randomly generated world will be solvable, not to mention interesting.
The main idea (it is by no means new) is the alternate use of the solver and generator. Let's start with a puzzle, which is probably unsolvable: just place two to five numbers in random squares of the cell:

Solver works until it can develop further:

Then the generator adds more information to the puzzle in the form of a point, after which the execution of the solver continues.

In this case, the added point to the solver is not enough for further development. Then the generator will continue to add new points until it satisfies the solver:

And then the solver continues his usual work:

This process continues either until the puzzle is solved, or until there is more information left to add (for example, when each cell that can be reached from the number already contains a point).
This method only works if the added new information cannot make any of the conclusions made earlier incorrect. This would be difficult to do when adding numbers to the grid [3] . But adding new points to the field has this property; at least for the reasoning rules that I use in this program.
Where should the algorithm add points? In the end, I decided to add them to the empty space, which can be closed in the initial state with as many lines as possible, so that each point seeks to give out as little information as possible. I did not try to specifically place the point in the place where it would be useful for advancement in solving the puzzle at the moment when the solver gets stuck. This creates a very convenient effect: most of the points at the beginning of the puzzle seem completely useless, which makes the puzzle more difficult than it really is. If all this is a lot of obvious moves that a player can make, but for some reason not one of them does not work properly. As a result, it turned out that the puzzle generator behaves a bit like a pig.
This process does not always create a solution, but it is quite fast (about 50-100 milliseconds), so to generate a level, you can simply repeat it several times. Unfortunately, he usually creates mediocre puzzles. From the very beginning there are too many obvious moves, the field fills up very quickly and the decision tree turns out to be rather shallow.
Optimizer
The process described above created mediocre puzzles. At the last stage, I use these levels as the basis for the optimization process. It works as follows.
The optimizer creates a pool that contains up to 10 puzzle options. The pool is initialized with a new generated random puzzle. At each iteration, the optimizer selects one puzzle from the pool and performs its mutation.
The mutation deletes all points, and then slightly changes the numbers (i.e. decreases / increases the value of a randomly selected number or moves the number to another cell in the grid). You can apply several mutations to the field at the same time. Then we run the solver in the special level generation mode described in the previous section. He adds enough points to the puzzle so that it becomes solvable again.
After that, we start the solver again, this time in normal mode. During this run, the solver monitors a) the depth of the decision tree, b) the frequency of the need for different types of rules, c) the width of the decision tree at different points in time. The puzzle is evaluated based on the criteria described above. The evaluation function prefers deep and narrow solutions, and levels of increased complexity also add more weight to puzzles in which more complex rules of reasoning are required.
Then a new puzzle is added to the pool. If the pool contains more than 10 puzzles, then the worst is discarded.
This process is repeated several times (approximately 10,000-50000 iterations took me). After that, the highest rated version of the puzzle is saved to the puzzle level database. Here's what the progress of the best puzzle in one optimization run looks like:

I tried using other ways to structure optimization. In one version, simulated annealing was used; others were genetic algorithms with various crossing-over operations. None of the solutions performed as well as a naive algorithm with a pool of options going back to the top.
Unique single solution
When a puzzle has a unique unique solution, an interesting difficulty arises. Is it possible to allow the player to assume that there is one solution and draw conclusions based on this? Would it be fair if the puzzle generator suggested that the player did so?
In a post on HackerNews, I said that there are four options for approaching this situation:
- Declare the uniqueness of the solution from the very beginning and force the generator to create levels that require this kind of reasoning. This is a bad decision because it complicates the understanding of the rules. And usually these are the details people forget.
- Do not guarantee the uniqueness of a decision: potentially have many decisions and make all of them. In fact, this does not solve the problem, but pushes it away.
- Just assume that this is a very rare event, which in practice is not important. (This is the solution that was used in the initial implementation.)
- Change the puzzle generator so that it does not generate puzzles in which knowledge of the uniqueness of the solution would help. (Probably the right solution, but requiring additional work.)
Initially, I chose the latter option, and that was a terrible mistake. It turned out that I took into account only one way in which the uniqueness of the solution led to information leakage, and it is actually quite rare. But there are others; one of them was in fact present at every level I generated and often led to the fact that the solution became trivial. Therefore, in May 2019, I changed the Hard and Expert modes using the third option.
The most annoying case is a deuce with a dashed line in this field:

Why can a cunning player make such a conclusion? A deuce can cover any of the four neighboring squares. None of them have dots, so they do not have to be covered by a line. And the square below does not have overlays with any other numbers. If there is a single solution, then this should be the case when other numbers cover the remaining three squares, and the two closes the square under it.
The solution is to add a few more points when recognizing such cases:

Another common case is a dash with a dotted line in this field:

The squares to the left and top of the two are no different. None of them have a point, and not one can be reached from any other number. Any solution in which a deuce covers the top square will have a corresponding solution in which it closes the left square, and vice versa. If there was a single unique solution, then this could not be, and the deuce should have covered the bottom square.
I decided this type of case in the way "if it hurts, then don’t touch it." Solver applied this rule at an early stage in the list of priorities and assigned such negative weight to such moves. Puzzles with this feature are usually discarded by the optimizer, and the few remaining are discarded at the stage of the final selection of levels for the published game.
This is not a complete list. During play testing with a deliberate search for errors, I found many other rules for unique solutions. But most of them seemed rare and they were enough to find, so they did not greatly simplify the game. If someone solves the puzzle using such reasoning, then I will not blame it on them.
Conclusion
Initially, the game was developed as an experiment in the procedural generation of puzzles. The game’s design and generator went hand in hand, so the techniques themselves are difficult to apply directly to other games.
The question to which I have no answer: has the investment of such efforts in procedural generation justified itself? Player feedback on level design was very controversial. In positive comments, it was usually said that some tricky trick is always felt in puzzles. In most negative reviews, they wrote to me that the game lacks a gradient of complexity.
I still have a couple of puzzles in their infancy, and I liked the generator so much that I most likely use a similar procedural approach for them. I’ll change only one thing: from the very beginning I will conduct active playtesting with the search for errors.
Notes
[0] Or, at least, it seemed to me. But when I watched the players live, almost half of them just made guesses, and then iterated through them. Anyway.
[1] Readers of my article should also read the article Solving Minesweeper and making it better Magnus Hoff.
[2] I’ll clarify that the depth / narrowness of a tree is a metric that I considered significant for my game, and not for all other puzzles. For example, there is a good argument that the Rush Hour puzzle is interesting if it has several ways to solve almost, but not exactly the same length. But it happened because Rush Hour is a game to find the shortest solution, and not just any solution.
[3] Excluding the addition of units. There were no dots in the first version of the puzzle, and the plan was for the generator to add units if necessary. But that seemed too restrictive.
