About bit counting, unsigned types in Kotlin and about situations where saving on matches is justified
This comment was prompted by the writing of the article . More precisely, one phrase from it.
... spending memory or processor cycles on items in billions of dollars is not good ...It so happened that recently I had to do just that. And, although, the case that I will consider in the article is rather special - the conclusions and applied solutions can be useful to someone.
A bit of context
The iFunny application deals with a huge amount of graphic and video content, and the fuzzy search for duplicates is one of the very important tasks. This in itself is a big topic that deserves a separate article, but today I’ll just talk a little about some approaches to calculating very large arrays of numbers in relation to this search. Of course, everyone has a different understanding of "very large arrays", and it would be foolish to compete with the Hadron Collider, but still. :)
If the algorithm is very short, then for each image its digital signature (signature) is created from 968 integers, and the comparison is made by finding the "distance" between the two signatures. Considering that the volume of content in the last two months alone amounted to about 10 million images, then an attentive reader will easily figure it out in his mind - these are exactly those “elements in billions of volumes.” Who cares - welcome to cat.
At the beginning there will be a boring story about saving time and memory, and at the end there will be a short instructive story about the fact that sometimes it is very useful to look at the source. A picture to attract attention is directly related to this instructive story.
I must admit that I was a little cunning. In a preliminary analysis of the algorithm, it was possible to reduce the number of values in each signature from 968 to 420. It is already twice as good, but the order of magnitude remains the same.
Although, if you think about it, I’m not so deceiving, and this will be the first conclusion: before starting the task, it’s worth thinking about - is it possible to somehow simplify it in advance?
The comparison algorithm is quite simple: the root of the sum of the squares of the differences of the two signatures is calculated, divided by the sum of the previously calculated values (i.e., in each iteration the summation will still be and it cannot be taken out to be a constant at all) and compared with the threshold value. It is worth noting that signature elements are limited to values from -2 to +2, and, accordingly, the absolute value of the difference is limited to values from 0 to 4.
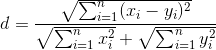
Nothing complicated, but quantity decides.
First approach, naive
// Порог
const val d = 0.3
// 10.000.000 объектов.
// Будем держать эту цифру в уме,
// чтобы не упоминать в каждом втором предложении
val collection: MutableList = mutableListOf()
// signature — массив из 420 значений типа Byte
class Signature(val signature: Array, val norma: Double)
fun getSimilar(signature: Signature) = collection
.filter { calculateDistance(it, signature) < d }
fun calculateDistance(first: Signature, second: Signature): Double =
Math.sqrt(first.signature.mapIndexed { index, value ->
Math.pow((value - second.signature[index]).toDouble(), 2.0)
}.sum()) / (first.norma + second.norma)
Let's calculate what we have here with the number of operations: the
10Msquare roots of Math.sqrt10Madditions and divisions of / (first.norma + second.norma)4.200Msubtractions and squaring Math.pow((value - second.signature[index]).toDouble(), 2.0)4.200Madditions .sum()What are our options:
- With such volumes, spending a whole
Byte(or, God forbid, someone would have guessed to useInt) storing three significant bits is an unforgivable waste. - Perhaps, how to reduce the amount of mathematics?
- But is it possible to do some preliminary filtering, which is not so computationally expensive?
The second approach, we pack
By the way, if someone suggests how you can simplify the calculations with such packaging, you will receive a big thank you and plus in karma. Although one, but from the bottom of my heart :)
One
Longis 64 bits, which, in our case, will allow us to store 21 values in it (and 1 bit will remain unsettled).// массив из 20 значений типа Long
class Signature(val signature: Array, val norma: Double)
fun calculateDistance(first: Signature, second: Signature): Double =
Math.sqrt(first.signature.mapIndexed { index, value ->
calculatePartial(value, second.signature[index])
}.sum()) / (first.norma + second.norma)
fun calculatePartial(first: Long, second: Long): Double {
var sum = 0L
(0..60 step 3).onEach {
val current = (first.ushr(it) and 0x7) - (second.ushr(it) and 0x7)
sum += current * current
}
return sum.toDouble()
}
It’s better from memory (
4.200Magainst 1.600Mbytes, if it's rude), but what about the calculations? I think it is obvious that the number of operations has remained the same and
8.400Mshifts and 8.400Mlogical I have been added to them . Maybe it can be optimized, but the trend is still not happy - this is not what we wanted.The third approach, re-pack with sub-subs
In the morning I can smell it, here you can use bit magic!
Let's store the values not in three, but in four bits. In this way:
| -2 | 0b1100 |
| -1 | 0b0100 |
| 0 | 0b0000 |
| 1 | 0b0010 |
| 2 | 0b0011 |
Yes, we will lose packing density in comparison with the previous version, but we will get the opportunity
XORto receive Long16 elements at once with differences (not quite). In addition, there will be only 11 options for the distribution of bits in each final nibble, which will allow you to use pre-calculated values of the squares of the differences.// массив из 27 значений типа Long
class Signature(val signature: Array, val norma: Double)
// -1 для невозможных вариантов
val precomputed = arrayOf(0, 1, 1, 4, 1, -1, 4, 9, 1, -1, -1, -1, 4, -1, 9, 16)
fun calculatePartial(first: Long, second: Long): Double {
var sum = 0L
val difference = first xor second
(0..60 step 4).onEach {
sum += precomputed[(difference.ushr(it) and 0xF).toInt()]
}
return sum.toDouble()
}
From memory it became
2.160Magainst 1.600M- unpleasant, but still better than the initial ones 4.200M. We calculate the steps of:
10Msquare roots, divisions and summations (did not disappear) 270MXOR's 4.320of additions, shifts and logical AND extracts from the array. It already looks more interesting, but, anyway, there are too many calculations. Unfortunately, it seems that we have already spent those 20% of the efforts giving 80% of the result and it's time to think about where else you can profit. The first thing that comes to mind is not to bring it to a calculation at all, filtering out obviously inappropriate signatures with some lightweight filter.
Fourth approach, large sieve
If you slightly transform the calculation formula, you can get this inequality (the smaller the calculated distance, the better):
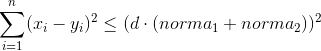
Those. now we need to figure out how to
Longcalculate the minimum possible value of the left side of the inequality based on the information we have on the number of bits set in the 'ah. Then simply discard all signatures that do not satisfy him. Let me remind you that x i can take values from 0 to 4 (the sign is not important, I think it’s clear why). Given that each term is squared, it is easy to derive a general pattern:
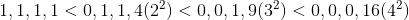
The final formula looks like this (we won’t need it, but I deduced it for a long time and it would be a shame to just forget and not show anyone):
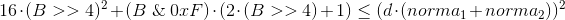
Where B is the number of bits set.
In fact,
Longthere are only 64 bits in one , read 64 possible results. And they are perfectly calculated in advance and added to an array, by analogy with the previous section. In addition, it is completely optional to calculate all 27
Long's - it is enough to exceed the threshold on the next of them and you can interrupt the check and return false. The same approach, by the way, can be used in the main calculation.fun getSimilar(signature: Signature) = collection
.asSequence() // Зачем нам лишняя промежуточная коллекция!?
.filter { estimate(it, signature) }
.filter { calculateDistance(it, signature) < d }
val estimateValues = arrayOf(0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 19, 22, 25, 28, 31, 34, 37, 40, 43, 46, 49, 52, 55, 58, 61, 64, 69, 74, 79, 84, 89, 94, 99, 104, 109, 114, 119, 124, 129, 134, 139, 144, 151, 158, 165, 172, 179, 186, 193, 200, 207, 214, 221, 228, 235, 242, 249, 256)
fun estimate(first: Signature, second: Signature):Boolean{
var bitThreshold = Math.pow(d * (first.norma + second.norma), 2.0).toLong()
first.signature.forEachIndexed { index, value ->
bitThreshold -= estimateValues[java.lang.Long.bitCount(value xor second.signature[index])]
if (bitThreshold <= 0) return false
}
return true
}
Here it must be understood that the effectiveness of this filter (up to negative) is disastrously dependent on the selected threshold and, slightly less strongly, on the input data. Fortunately, for the threshold we need, a
d=0.3fairly small number of objects succeed in passing the filter, and the contribution of their calculation to the total response time is so meager that they can be neglected. And if so, then you can save a little more.Fifth approach, getting rid of sequence
When working with large collections,
sequencethis is a good protection against the extremely unpleasant Out of memory . However, if we obviously know that on the first filter the collection will be reduced to a sane size, then it would be a much more reasonable choice to use ordinary enumeration in a loop with the creation of an intermediate collection, because it sequenceis not only fashionable and youthful, but also an iterator, in which hasNextcompanions who are not free at all.fun getSimilar(signature: Signature) = collection
.filter { estimate(it, signature) }
.filter { calculateDistance(it, signature) < d }
It would seem that here it is happiness, but I wanted to "make it beautiful." Here we come to the promised instructive story.
Sixth approach, we wanted the best
We write on Kotlin, and here are some foreign ones
java.lang.Long.bitCount! And more recently, unsigned types were brought into the language. Attack! No sooner said than done. All
Longreplaced by ULong, from the Java source with the root torn out java.lang.Long.bitCountand rewritten as an extension function forULongfun ULong.bitCount(): Int {
var i = this
i = i - (i.shr(1) and 0x5555555555555555uL)
i = (i and 0x3333333333333333uL) + (i.shr(2) and 0x3333333333333333uL)
i = i + i.shr(4) and 0x0f0f0f0f0f0f0f0fuL
i = i + i.shr(8)
i = i + i.shr(16)
i = i + i.shr(32)
return i.toInt() and 0x7f
}
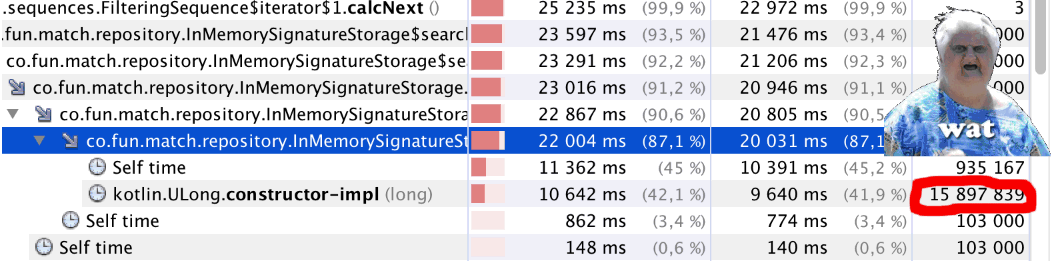
We start and ... Something is wrong. The code began to work out noticeably slower. We start the profiler and see something strange (see the heading of the article): a little less than a million calls,
bitCount()almost 16 million calls Kotlin.ULong.constructor-impl. WAT !? The riddle is explained simply - just look into the class code
ULongpublic inline class ULong @PublishedApi internal constructor(@PublishedApi internal val data: Long) : Comparable {
@kotlin.internal.InlineOnly
public inline operator fun plus(other: ULong): ULong = ULong(this.data.plus(other.data))
@kotlin.internal.InlineOnly
public inline operator fun minus(other: ULong): ULong = ULong(this.data.minus(other.data))
@kotlin.internal.InlineOnly
public inline infix fun shl(bitCount: Int): ULong = ULong(data shl bitCount)
@kotlin.internal.InlineOnly
public inline operator fun inc(): ULong = ULong(data.inc())
и т.д.
}
No, I understand everything
ULongnow experimental, but how so !? In general, we recognize the approach as failed, which is a pity.
Well, but still, maybe something else can be improved?
Actually, you can. The original code
java.lang.Long.bitCountis not the most optimal. It gives a good result in the general case, but if we know in advance on which processors our application will work, then we can choose a more optimal way - here is a very good article about it on Habré. I thoroughly recommend counting single bits , I highly recommend reading it. I used the "Combined Method"
fun Long.bitCount(): Int {
var n = this
n -= (n.shr(1)) and 0x5555555555555555L
n = ((n.shr(2)) and 0x3333333333333333L) + (n and 0x3333333333333333L)
n = ((((n.shr(4)) + n) and 0x0F0F0F0F0F0F0F0FL) * 0x0101010101010101).shr(56)
return n.toInt() and 0x7F
}
Counting parrots
All measurements were made haphazardly, during development on the local machine and are reproduced from memory, so it’s difficult to talk about any accuracy, but you can estimate the approximate contribution of each approach.
| What they were doing | parrots (seconds) |
|---|---|
| First approach, naive | 25 ± |
| The second approach, we pack | - |
| The third approach, re-pack with sub-subs | 11-14 |
| Fourth approach, large sieve | 2-3 |
| Fifth approach, getting rid of sequence | 1.8-2.2 |
| Sixth approach, we wanted the best | 3-4 |
| "Combined method" for counting the set bits | 1.5-1.7 |
conclusions
- When dealing with the processing of large amounts of data, it is worth spending time on a preliminary analysis. Perhaps not all of this data needs to be processed.
- If you can use coarse, but cheap pre-filtering, this can help a lot.
- Bit magic is our everything. Well, where applicable, of course.
- To look at source codes of standard classes and functions is sometimes very useful.
Thanks for attention! :)
And yes, to be continued.
