Creating a reliable and verified AI: compliance with specifications, reliable training and formal verification
- Transfer
Errors and software went hand in hand from the very beginning of the era of computer programming. Over time, developers have developed a set of practices for testing and debugging programs before they are deployed, but these practices are no longer suitable for modern systems with deep learning. Today, the main practice in the field of machine learning can be called training on a particular data set, followed by verification on another set. In this way, you can calculate the average efficiency of the models, but it is also important to guarantee reliability, that is, acceptable efficiency in the worst case. In this article, we describe three approaches for accurately identifying and eliminating errors in trained predictive models: adversarial testing, robust learning, and formal verification[formal verification].
Systems with MOs are, by definition, not stable. Even systems that win against a person in a certain area may not be able to cope with the solution of simple problems when making subtle differences. For example, consider the problem of introducing disturbances in images: a neural network that can classify images better than people can easily be made to believe that the sloth is a race car, adding a small fraction of carefully calculated noise to the image.

Competing input when overlaid on a regular image can confuse AI. Two extreme images differ by no more than 0.0078 for each pixel. The first is classified as a sloth, with a 99% probability. The second is like a race car with 99% probability.
This problem is not new. Programs have always had errors. For decades, programmers have been gaining an impressive array of techniques, from unit testing to formal verification. On traditional programs, these methods work well, but adapting these approaches for rigorous testing of MO models is extremely difficult due to the scale and lack of structure in models that can contain hundreds of millions of parameters. This suggests the need to develop new approaches to ensure the reliability of MO systems.
From the point of view of the programmer, a bug is any behavior that does not meet the specification, that is, the planned functionality of the system. As part of our AI research, we are studying techniques for assessing whether MO systems meet the requirements not only on the training and test sets, but also on the list of specifications that describe the desired properties of the system. Among these properties there may be resistance to sufficiently small changes in the input data, safety restrictions that prevent catastrophic failures, or compliance of predictions with the laws of physics.
In this article, we will discuss three important technical issues that the MO community faces in working to make the MO systems robust and reliably consistent with the desired specifications:
Resistance to competitive examples is a fairly well-studied problem of civil defense. One of the main conclusions made is the importance of evaluating the network's actions as a result of strong attacks, and the development of transparent models that can be analyzed quite effectively. We, along with other researchers, have found that many models turn out to be stable against weak, competitive examples. However, they provide almost 0% accuracy for stronger competitive examples ( Athalye et al., 2018 , Uesato et al., 2018 , Carlini and Wagner, 2017 ).
Although most of the work focuses on rare failures in the context of teaching with a teacher (and this is mainly a classification of images), there is a need to expand the application of these ideas to other areas. In a recent work with a competitive approach to catastrophic failures, we apply these ideas to testing networks trained with reinforcements and designed for use in places with high security requirements. One of the challenges of developing autonomous systems is that, since one error can have serious consequences, even a small probability of failure is not considered acceptable.
Our goal is to design a “rival” that will help to recognize such errors in advance (in a controlled environment). If an adversary can effectively determine the worst input data for a given model, this will allow us to catch rare cases of failures before deploying it. As with image classifiers, evaluating how to work with a weak opponent gives you a false sense of security during deployment. This approach is similar to software development using the “red team” [red-teaming - involving a third-party development team that takes on the role of attackers to detect vulnerabilities / approx. transl.], however, it goes beyond the search for failures caused by intruders, and also includes errors that occur naturally, for example, due to insufficient generalization.
We have developed two complementary approaches to competitive testing of reinforced learning networks. In the first, we use derivative-free optimization to directly minimize the expected reward. In the second, we learn a function of adversarial value, which in experience predicts in which situations the network may fail. Then we use this learned function for optimization, concentrating on evaluating the most problematic input data. These approaches form only a small part of the rich and growing space of potential algorithms, and we are very interested in the future development of this area.
Both approaches are already showing significant improvements over random testing. Using our method, in a few minutes it is possible to detect flaws that previously had to be searched for all day, or perhaps could not be found at all ( Uesato et al., 2018b ). We also found that adversarial testing can reveal a qualitatively different behavior of networks compared to what might be expected from an evaluation on a random test set. In particular, using our method, we found that networks that performed the orientation task on a three-dimensional map, and usually cope with this at the human level, cannot find the target in unexpectedly simple labyrinths ( Ruderman et al., 2018) Our work also emphasizes the need to design systems that are safe against natural failures, and not just rivals.

Conducting tests on random samples, we almost never see cards with a high probability of failure, but competitive testing shows the existence of such cards. The probability of failure remains high even after removing many walls, that is, simplifying maps compared to the original ones.
Competitive testing attempts to find a counterexample that violates specifications. Often, it overestimates model consistency with these specifications. From a mathematical point of view, the specification is a kind of relationship that must be maintained between the input and output data of the network. It can take the form of an upper and lower boundary or some key input and output parameters.
Inspired by this observation, several researchers ( Raghunathan et al., 2018 ; Wong et al., 2018 ; Mirman et al., 2018 ; Wang et al., 2018 ), including our team from DeepMind ( Dvijotham et al., 2018 ; Gowal et al., 2018), worked on algorithms invariant to competitive testing. It can be described geometrically - we can limit ( Ehlers 2017 , Katz et al. 2017 , Mirman et al., 2018 ) the worst violation of the specification, limiting the space of output data based on a set of input. If this boundary is differentiable by network parameters and can be quickly calculated, it can be used during training. Then, the original boundary can propagate through each layer of the network.
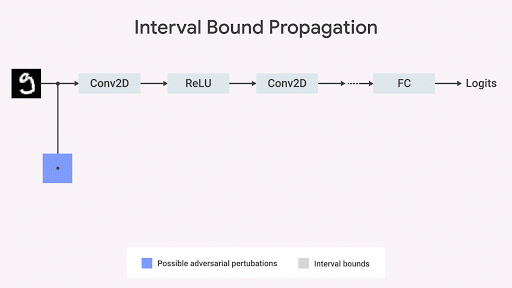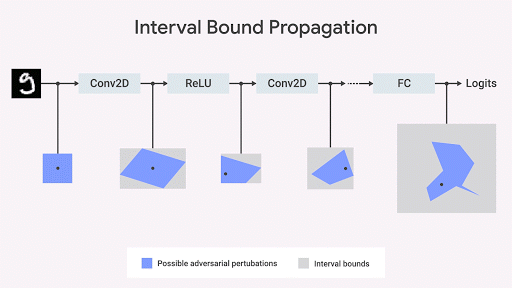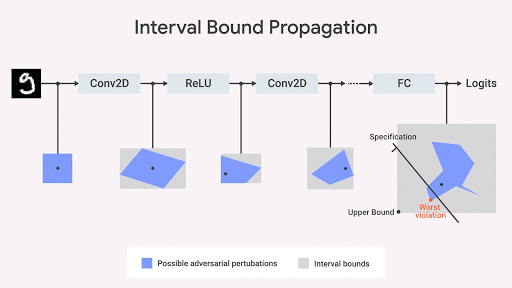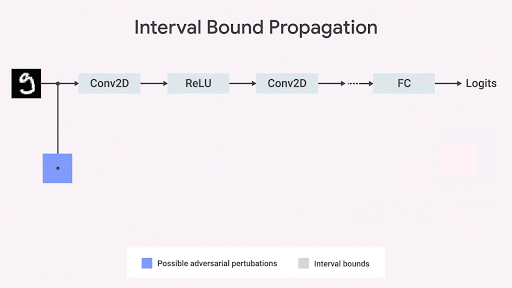
We show that the spread of the boundary of the interval is fast, efficient, and - unlike what was previously thought - gives good results ( Gowal et al., 2018) In particular, we show that it can provably reduce the number of errors (i.e., the maximum number of errors that any opponent can cause) compared to the most advanced image classifiers on sets from the MNIST and CIFAR-10 databases.
The next goal will be to study the correct geometric abstractions to calculate excessive approximations of the output space. We also want to train networks so that they work reliably with more complex specifications that describe the desired behavior, such as the previously mentioned invariance and compliance with physical laws.
Thorough testing and training can be of great help in creating reliable MO systems. However, formally arbitrarily voluminous testing cannot guarantee that the behavior of the system matches our desires. In large-scale models, enumerating all possible output options for a given set of input (for example, minor image changes) seems difficult to implement due to the astronomical number of possible image changes. However, as in the case of training, one can find more effective approaches to setting geometric constraints on the set of output data. Formal verification is the subject of ongoing research at DeepMind.
The MO community has developed some interesting ideas for computing the exact geometric boundaries of the network output space (Katz et al. 2017, Weng et al., 2018 ; Singh et al., 2018 ). Our Approach ( Dvijotham et al., 2018), based on optimization and duality, consists of formulating the verification problem in terms of optimization, which is trying to find the largest violation of the property being tested. The task becomes computable if ideas from duality are used in optimization. As a result, we obtain additional constraints that specify the boundaries calculated when moving the interval bound [interval bound propagation] using the so-called cutting planes. This is a reliable but incomplete approach: there may be cases when the property of interest to us is satisfied, but the boundary calculated by this algorithm is not strict enough so that the presence of this property can be formally proved. However, having received the border, we get a formal guarantee of the absence of violations of this property. In fig. Below this approach is illustrated graphically.

This approach allows us to expand the applicability of verification algorithms on more general-purpose networks (activator functions, architectures), general specifications and more complex GO models (generative models, neural processes, etc.) and specifications that go beyond competitive reliability ( Qin , 2018 ).
Deploying MOs in high-risk situations has its own unique challenges and difficulties, and this requires the development of assessment technologies that are guaranteed to detect unlikely errors. We believe that consistent training on specifications can significantly improve performance compared to cases where specifications arise implicitly from training data. We look forward to the results of ongoing competitive assessment studies, robust training models, and verification of formal specifications.
It will take a lot of work so that we can create automated tools that guarantee that AI systems in the real world will "do everything right." In particular, we are very pleased to progress in the following areas:
DeepMind is committed to positively impacting society through the responsible development and deployment of MO systems. To make sure that the contribution of developers is guaranteed to be positive, we need to deal with many technical obstacles. We intend to contribute to this area and are happy to work with the community to resolve these issues.
Systems with MOs are, by definition, not stable. Even systems that win against a person in a certain area may not be able to cope with the solution of simple problems when making subtle differences. For example, consider the problem of introducing disturbances in images: a neural network that can classify images better than people can easily be made to believe that the sloth is a race car, adding a small fraction of carefully calculated noise to the image.

Competing input when overlaid on a regular image can confuse AI. Two extreme images differ by no more than 0.0078 for each pixel. The first is classified as a sloth, with a 99% probability. The second is like a race car with 99% probability.
This problem is not new. Programs have always had errors. For decades, programmers have been gaining an impressive array of techniques, from unit testing to formal verification. On traditional programs, these methods work well, but adapting these approaches for rigorous testing of MO models is extremely difficult due to the scale and lack of structure in models that can contain hundreds of millions of parameters. This suggests the need to develop new approaches to ensure the reliability of MO systems.
From the point of view of the programmer, a bug is any behavior that does not meet the specification, that is, the planned functionality of the system. As part of our AI research, we are studying techniques for assessing whether MO systems meet the requirements not only on the training and test sets, but also on the list of specifications that describe the desired properties of the system. Among these properties there may be resistance to sufficiently small changes in the input data, safety restrictions that prevent catastrophic failures, or compliance of predictions with the laws of physics.
In this article, we will discuss three important technical issues that the MO community faces in working to make the MO systems robust and reliably consistent with the desired specifications:
- Effective verification of compliance with specifications. We are studying effective ways to verify that MO systems correspond to their properties (for example, such as stability and invariance) that are required from them by the developer and users. One approach to finding cases in which the model can move away from these properties is a systematic search for the worst work results.
- Training MO models to specifications. Even if there is a sufficiently large amount of training data, standard MO algorithms can produce predictive models whose operation does not meet the desired specifications. We are required to revise the training algorithms so that they not only work well on the training data, but also meet the desired specifications.
- Formal proof of the conformity of MO models to desired specifications. Algorithms must be developed to confirm that the model meets the desired specifications for all possible input data. Although the field of formal verification has studied such algorithms for several decades, despite its impressive progress, these approaches are not easy to scale to modern MO systems.
Verify Model Compliance with Desired Specifications
Resistance to competitive examples is a fairly well-studied problem of civil defense. One of the main conclusions made is the importance of evaluating the network's actions as a result of strong attacks, and the development of transparent models that can be analyzed quite effectively. We, along with other researchers, have found that many models turn out to be stable against weak, competitive examples. However, they provide almost 0% accuracy for stronger competitive examples ( Athalye et al., 2018 , Uesato et al., 2018 , Carlini and Wagner, 2017 ).
Although most of the work focuses on rare failures in the context of teaching with a teacher (and this is mainly a classification of images), there is a need to expand the application of these ideas to other areas. In a recent work with a competitive approach to catastrophic failures, we apply these ideas to testing networks trained with reinforcements and designed for use in places with high security requirements. One of the challenges of developing autonomous systems is that, since one error can have serious consequences, even a small probability of failure is not considered acceptable.
Our goal is to design a “rival” that will help to recognize such errors in advance (in a controlled environment). If an adversary can effectively determine the worst input data for a given model, this will allow us to catch rare cases of failures before deploying it. As with image classifiers, evaluating how to work with a weak opponent gives you a false sense of security during deployment. This approach is similar to software development using the “red team” [red-teaming - involving a third-party development team that takes on the role of attackers to detect vulnerabilities / approx. transl.], however, it goes beyond the search for failures caused by intruders, and also includes errors that occur naturally, for example, due to insufficient generalization.
We have developed two complementary approaches to competitive testing of reinforced learning networks. In the first, we use derivative-free optimization to directly minimize the expected reward. In the second, we learn a function of adversarial value, which in experience predicts in which situations the network may fail. Then we use this learned function for optimization, concentrating on evaluating the most problematic input data. These approaches form only a small part of the rich and growing space of potential algorithms, and we are very interested in the future development of this area.
Both approaches are already showing significant improvements over random testing. Using our method, in a few minutes it is possible to detect flaws that previously had to be searched for all day, or perhaps could not be found at all ( Uesato et al., 2018b ). We also found that adversarial testing can reveal a qualitatively different behavior of networks compared to what might be expected from an evaluation on a random test set. In particular, using our method, we found that networks that performed the orientation task on a three-dimensional map, and usually cope with this at the human level, cannot find the target in unexpectedly simple labyrinths ( Ruderman et al., 2018) Our work also emphasizes the need to design systems that are safe against natural failures, and not just rivals.

Conducting tests on random samples, we almost never see cards with a high probability of failure, but competitive testing shows the existence of such cards. The probability of failure remains high even after removing many walls, that is, simplifying maps compared to the original ones.
Spec Model Training
Competitive testing attempts to find a counterexample that violates specifications. Often, it overestimates model consistency with these specifications. From a mathematical point of view, the specification is a kind of relationship that must be maintained between the input and output data of the network. It can take the form of an upper and lower boundary or some key input and output parameters.
Inspired by this observation, several researchers ( Raghunathan et al., 2018 ; Wong et al., 2018 ; Mirman et al., 2018 ; Wang et al., 2018 ), including our team from DeepMind ( Dvijotham et al., 2018 ; Gowal et al., 2018), worked on algorithms invariant to competitive testing. It can be described geometrically - we can limit ( Ehlers 2017 , Katz et al. 2017 , Mirman et al., 2018 ) the worst violation of the specification, limiting the space of output data based on a set of input. If this boundary is differentiable by network parameters and can be quickly calculated, it can be used during training. Then, the original boundary can propagate through each layer of the network.

We show that the spread of the boundary of the interval is fast, efficient, and - unlike what was previously thought - gives good results ( Gowal et al., 2018) In particular, we show that it can provably reduce the number of errors (i.e., the maximum number of errors that any opponent can cause) compared to the most advanced image classifiers on sets from the MNIST and CIFAR-10 databases.
The next goal will be to study the correct geometric abstractions to calculate excessive approximations of the output space. We also want to train networks so that they work reliably with more complex specifications that describe the desired behavior, such as the previously mentioned invariance and compliance with physical laws.
Formal verification
Thorough testing and training can be of great help in creating reliable MO systems. However, formally arbitrarily voluminous testing cannot guarantee that the behavior of the system matches our desires. In large-scale models, enumerating all possible output options for a given set of input (for example, minor image changes) seems difficult to implement due to the astronomical number of possible image changes. However, as in the case of training, one can find more effective approaches to setting geometric constraints on the set of output data. Formal verification is the subject of ongoing research at DeepMind.
The MO community has developed some interesting ideas for computing the exact geometric boundaries of the network output space (Katz et al. 2017, Weng et al., 2018 ; Singh et al., 2018 ). Our Approach ( Dvijotham et al., 2018), based on optimization and duality, consists of formulating the verification problem in terms of optimization, which is trying to find the largest violation of the property being tested. The task becomes computable if ideas from duality are used in optimization. As a result, we obtain additional constraints that specify the boundaries calculated when moving the interval bound [interval bound propagation] using the so-called cutting planes. This is a reliable but incomplete approach: there may be cases when the property of interest to us is satisfied, but the boundary calculated by this algorithm is not strict enough so that the presence of this property can be formally proved. However, having received the border, we get a formal guarantee of the absence of violations of this property. In fig. Below this approach is illustrated graphically.

This approach allows us to expand the applicability of verification algorithms on more general-purpose networks (activator functions, architectures), general specifications and more complex GO models (generative models, neural processes, etc.) and specifications that go beyond competitive reliability ( Qin , 2018 ).
Prospects
Deploying MOs in high-risk situations has its own unique challenges and difficulties, and this requires the development of assessment technologies that are guaranteed to detect unlikely errors. We believe that consistent training on specifications can significantly improve performance compared to cases where specifications arise implicitly from training data. We look forward to the results of ongoing competitive assessment studies, robust training models, and verification of formal specifications.
It will take a lot of work so that we can create automated tools that guarantee that AI systems in the real world will "do everything right." In particular, we are very pleased to progress in the following areas:
- Training for competitive assessment and verification. With the scaling and complication of AI systems, it is becoming increasingly difficult to design competitive assessment and verification algorithms that are sufficiently adapted to the AI model. If we can use the full power of AI for evaluation and verification, this process can be scaled.
- Development of publicly available tools for competitive assessment and verification: it is important to provide engineers and other AI-using people with easy-to-use tools that shed light on possible modes of failure of the AI system before this failure leads to extensive negative consequences. This will require some standardization of competitive assessments and verification algorithms.
- Expanding the spectrum of competitive examples. So far, most of the work on competitive examples has focused on the stability of models to small changes, usually in the field of pictures. This has become an excellent testing ground for developing approaches to competitive assessments, reliable training and verification. We began to study various specifications for properties that are directly related to the real world, and we look forward to the results of future research in this direction.
- Training specifications. Specifications that describe the “correct” behavior of AI systems are often difficult to formulate accurately. As we create more and more intelligent systems capable of complex behavior and work in an unstructured environment, we will need to learn how to create systems that can use partially formulated specifications, and obtain further specifications from feedback.
DeepMind is committed to positively impacting society through the responsible development and deployment of MO systems. To make sure that the contribution of developers is guaranteed to be positive, we need to deal with many technical obstacles. We intend to contribute to this area and are happy to work with the community to resolve these issues.
