Creation of a formal verification system from scratch. Part 1: character virtual machine in PHP and Python
Formal verification is the verification of one program or algorithm using another.
This is one of the most powerful methods that allows you to find all vulnerabilities in the program or to prove that they are not there.
A more detailed description of formal verification can be seen on the example of solving the problem of Wolf, Goat, and cabbage in my previous article.
In this article, I move from formal verification of tasks to programs, and describe
how you can convert them into formal rule systems automatically.
For this, I wrote my analogue of a virtual machine, on symbolic principles.
She parses the program code and translates it into a system of equations (SMT), which can already be solved programmatically.
Since information about symbolic calculations is presented on the Internet quite fragmentarily,
I will briefly describe what it is.
Character calculations are a way of simultaneously executing a program on a wide range of data and are the main tool for formal verification of programs.
For example, we can set the input conditions where the first argument can take any positive values, the second negative, the third zero, and the output argument, for example, 42.
Symbolic calculations in one run will give us the answer, is it possible for us to obtain the desired result and an example set such input parameters. Or the proof that there are no such parameters.
Moreover, we can set the input arguments in general as all possible, and select only the output, for example, the administrator password.
In this case, we will find all the vulnerabilities of the program or we will get proof that the admin password is safe.
You may notice that the classical execution of a program with specific input data is a special case of a symbolic one.
Therefore, my character VM can also work in the emulation mode of a standard virtual machine.
In the comments to the previous article, you can find a fair criticism of formal verification with a discussion of its weaknesses.
The main problems are as follows:
As a result, the program will be verified and meet the specifications, but it will not do at all what the creators expected from it.
Since in this article I mainly consider the application of formal verification in practice, I will not beat my forehead against the wall yet, and I will choose a system where the algorithmic complexity and the number of external calls are minimal.
Since smart contracts suit these requirements in the best way, the choice fell on RIDE contracts from the Waves platform: they are not Turing-complete, and their maximum complexity is artificially limited.
But we will consider them solely from the technical side.
In addition to all, for any contracts, formal verification will be especially in demand: as a rule, it is impossible to correct a contract error after its launch.
And the price of such errors can be very high, since rather large amounts of funds are often stored on smart contracts.
My character virtual machine is written in PHP and Python, and uses Microsoft Research's Z3Prover to solve the resulting SMT formulas.
At its core lies a powerful multi-transactional search that
allows you to find solutions or vulnerabilities, even if it requires a lot of transactions.
Even Mythril , one of the most powerful symbolic frameworks for searching Ethereum vulnerabilities, added this feature only a few months ago.
But it is worth noting that ether contracts are more complex and have Turing completeness.
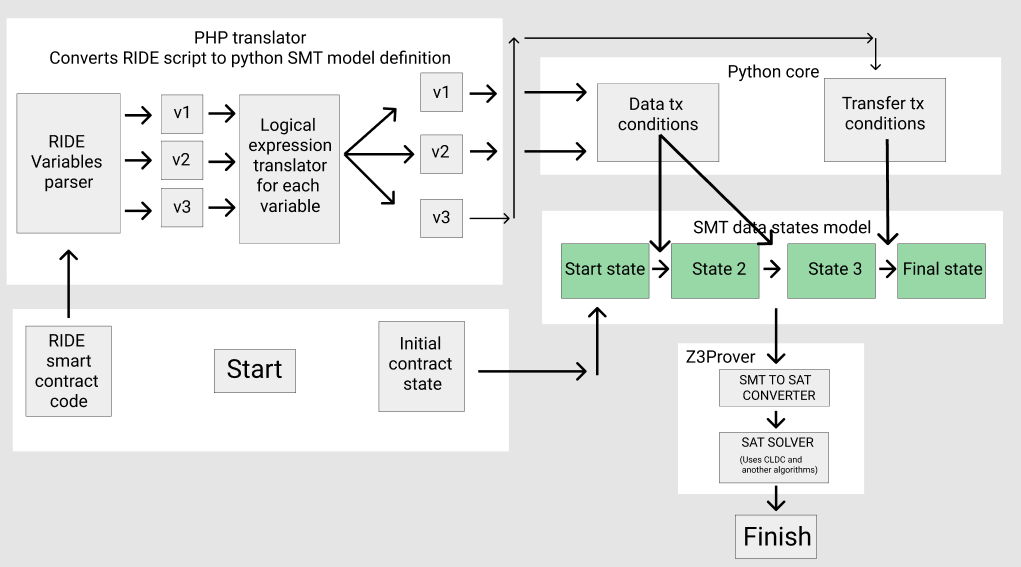
PHP translates the source code of the RIDE smart contract into a python script in which the program is presented in the form of a system of contract conditions and conditions for their transition compatible with Z3 SMT:
Now I will describe in more detail what is happening inside.
But first, a few words about the language of smart contracts RIDE.
It is a functional and expression-based programming language that is lazy as intended.
RIDE is performed in isolation within the blockchain, and can extract and write information from the storage associated with the wallet of the user.
You can attach a RIDE contract to each wallet, and the result of the execution will be only TRUE or FALSE.
TRUE means that the smart contract allows the transaction, and FALSE that it forbids it.
A simple example: a script can prohibit a transfer if the wallet balance is less than 100.
As an example, I will take the same Wolf, Goat, and Cabbage, but already presented in the form of a smart contract.
The user will not be able to withdraw money from the wallet on which the contract is deployed until he forwards everyone to the other side.
PHP first of all extracts from the smart contract all the variables in the form of their keys and the corresponding variable of the logical expression.
PHP then converts them into a compatible Python system description for Z3Prover SMT.
The data is wrapped in a cycle where the storage variables get index i, transaction variables index i + 1, and variables with expressions set the rules for the transition from the previous state to the next.
This is the very heart of our virtual machine, which provides a multi-transactional search engine.
Conditions are sorted and inserted into a script template designed to describe the SMT system in python.
For the last state from the entire chain, the rules that are specified in the transfer transaction section apply.
So, Z3Prover will look for just such a set of conditions that will eventually allow you to withdraw funds from the contract.
As a result, we automatically get a fully working SMT model of our contract.
You can see that it is very similar to the model from my previous article, which I wrote manually.
After launch, Z3Prover solves a smart contract and displays a transaction chain to us, which will allow us to withdraw funds:
In addition to the forwarding contract, you can experiment with your own contracts or try this simple example, which is solved in 2 transactions.
Since this is the very first version, the syntax is very limited and bugs can occur.
In the following articles, I plan to highlight the further development of VM, and show how it is possible to create formally verified smart contracts with its help, and not just solve them.
A symbolic virtual machine is available at http://2.59.42.98/hyperbox/
Sources are available on github: http://github.com/scp1001/hyperbox
All VM logic is contained in 2 files, hyperbox.php and hyperbox2.php
This is one of the most powerful methods that allows you to find all vulnerabilities in the program or to prove that they are not there.
A more detailed description of formal verification can be seen on the example of solving the problem of Wolf, Goat, and cabbage in my previous article.
In this article, I move from formal verification of tasks to programs, and describe
how you can convert them into formal rule systems automatically.
For this, I wrote my analogue of a virtual machine, on symbolic principles.
She parses the program code and translates it into a system of equations (SMT), which can already be solved programmatically.
Since information about symbolic calculations is presented on the Internet quite fragmentarily,
I will briefly describe what it is.
Character calculations are a way of simultaneously executing a program on a wide range of data and are the main tool for formal verification of programs.
For example, we can set the input conditions where the first argument can take any positive values, the second negative, the third zero, and the output argument, for example, 42.
Symbolic calculations in one run will give us the answer, is it possible for us to obtain the desired result and an example set such input parameters. Or the proof that there are no such parameters.
Moreover, we can set the input arguments in general as all possible, and select only the output, for example, the administrator password.
In this case, we will find all the vulnerabilities of the program or we will get proof that the admin password is safe.
You may notice that the classical execution of a program with specific input data is a special case of a symbolic one.
Therefore, my character VM can also work in the emulation mode of a standard virtual machine.
In the comments to the previous article, you can find a fair criticism of formal verification with a discussion of its weaknesses.
The main problems are as follows:
- Combinatorial explosion, since formal verification ultimately rests on P = NP
- Handling calls to the file system, networks and other external storage is more difficult to verify
- Bugs in the specification, when the customer or programmer conceived one thing, but did not accurately describe it in the statement of work.
As a result, the program will be verified and meet the specifications, but it will not do at all what the creators expected from it.
Since in this article I mainly consider the application of formal verification in practice, I will not beat my forehead against the wall yet, and I will choose a system where the algorithmic complexity and the number of external calls are minimal.
Since smart contracts suit these requirements in the best way, the choice fell on RIDE contracts from the Waves platform: they are not Turing-complete, and their maximum complexity is artificially limited.
But we will consider them solely from the technical side.
In addition to all, for any contracts, formal verification will be especially in demand: as a rule, it is impossible to correct a contract error after its launch.
And the price of such errors can be very high, since rather large amounts of funds are often stored on smart contracts.
My character virtual machine is written in PHP and Python, and uses Microsoft Research's Z3Prover to solve the resulting SMT formulas.
At its core lies a powerful multi-transactional search that
allows you to find solutions or vulnerabilities, even if it requires a lot of transactions.
Even Mythril , one of the most powerful symbolic frameworks for searching Ethereum vulnerabilities, added this feature only a few months ago.
But it is worth noting that ether contracts are more complex and have Turing completeness.
PHP translates the source code of the RIDE smart contract into a python script in which the program is presented in the form of a system of contract conditions and conditions for their transition compatible with Z3 SMT:

Now I will describe in more detail what is happening inside.
But first, a few words about the language of smart contracts RIDE.
It is a functional and expression-based programming language that is lazy as intended.
RIDE is performed in isolation within the blockchain, and can extract and write information from the storage associated with the wallet of the user.
You can attach a RIDE contract to each wallet, and the result of the execution will be only TRUE or FALSE.
TRUE means that the smart contract allows the transaction, and FALSE that it forbids it.
A simple example: a script can prohibit a transfer if the wallet balance is less than 100.
As an example, I will take the same Wolf, Goat, and Cabbage, but already presented in the form of a smart contract.
The user will not be able to withdraw money from the wallet on which the contract is deployed until he forwards everyone to the other side.
#Извлекаем положение всех объектов из блокчейна
let contract = tx.sender
let human= extract(getInteger(contract,"human"))
let wolf= extract(getInteger(contract,"wolf"))
let goat= extract(getInteger(contract,"goat"))
let cabbage= extract(getInteger(contract,"cabbage"))
#Это так называемая дата-транзакция, в которой пользователь присылает новые 4 переменные.
#Контракт разрешит её только в случае если все объекты останутся в сохранности.
match tx {
case t:DataTransaction =>
#Извлекаем будущее положение всех объектов из транзакции
let newHuman= extract(getInteger(t.data,"human"))
let newWolf= extract(getInteger(t.data,"wolf"))
let newGoat= extract(getInteger(t.data,"goat"))
let newCabbage= extract(getInteger(t.data,"cabbage"))
#0 обозначает, что объект на левом берегу, а 1 что на правом
let humanSide= human == 0 || human == 1
let wolfSide= wolf == 0 || wolf == 1
let goatSide= goat == 0 || goat == 1
let cabbageSide= cabbage == 0 || cabbage == 1
let side= humanSide && wolfSide && goatSide && cabbageSide
#Будут разрешены только те транзакции, где с козой никого нет в отсутствии фермера.
let safeAlone= newGoat != newWolf && newGoat != newCabbage
let safe= safeAlone || newGoat == newHuman
let humanTravel= human != newHuman
#Способы путешествия фермера туда и обратно, с кем-то либо в одиночку.
let t1= humanTravel && newWolf == wolf + 1 && newGoat == goat && newCabbage == cabbage
let t2= humanTravel && newWolf == wolf && newGoat == goat + 1 && newCabbage == cabbage
let t3= humanTravel && newWolf == wolf && newGoat == goat && newCabbage == cabbage + 1
let t4= humanTravel && newWolf == wolf - 1 && newGoat == goat && newCabbage == cabbage
let t5= humanTravel && newWolf == wolf && newGoat == goat - 1 && newCabbage == cabbage
let t6= humanTravel && newWolf == wolf && newGoat == goat && newCabbage == cabbage - 1
let t7= humanTravel && newWolf == wolf && newGoat == goat && newCabbage == cabbage
let objectTravel = t1 || t2 || t3 || t4 || t5 || t6 || t7
#Последняя строка в разделе транзакции описывает разрешающее транзакцию условие.
#Переменные транзакции должны иметь значения 1 или 0, все объекты должны
#быть в безопасности, а фермер должен переплывать реку в одиночку
#или с кем-то на каждом шагу
side && safe && humanTravel && objectTravel
case s:TransferTransaction =>
#Транзакция вывода средств разрешена только в случае если все переплыли на другой берег
human == 1 && wolf == 1 && goat == 1 && cabbage == 1
#Все прочие типы транзакций запрещены
case _ => false
}
PHP first of all extracts from the smart contract all the variables in the form of their keys and the corresponding variable of the logical expression.
cabbage: extract ( getInteger ( contract , "cabbage" ) )
goat: extract ( getInteger ( contract , "goat" ) )
human: extract ( getInteger ( contract , "human" ) )
wolf: extract ( getInteger ( contract , "wolf" ) )
fState: human== 1 && wolf== 1 && goat== 1 && cabbage== 1
fState:
wolf:
goat:
cabbage:
cabbageSide: cabbage== 0 || cabbage== 1
human: extract ( getInteger ( contract , "human" ) )
newGoat: extract ( getInteger ( t.data , "goat" ) )
newHuman: extract ( getInteger ( t.data , "human" ) )
goatSide: goat== 0 || goat== 1
humanSide: human== 0 || human== 1
t7: humanTravel && newWolf== wolf && newGoat== goat && newCabbage== cabbage
t3: humanTravel && newWolf== wolf && newGoat== goat && newCabbage== cabbage + 1
t6: humanTravel && newWolf== wolf && newGoat== goat && newCabbage== cabbage - 1
t2: humanTravel && newWolf== wolf && newGoat== goat + 1 && newCabbage== cabbage
t5: humanTravel && newWolf== wolf && newGoat== goat - 1 && newCabbage== cabbage
t1: humanTravel && newWolf== wolf + 1 && newGoat== goat && newCabbage== cabbage
t4: humanTravel && newWolf== wolf - 1 && newGoat== goat && newCabbage== cabbage
safeAlone: newGoat != newWolf && newGoat != newCabbage
wolfSide: wolf== 0 || wolf== 1
humanTravel: human != newHuman
side: humanSide && wolfSide && goatSide && cabbageSide
safe: safeAlone || newGoat== newHuman
objectTravel: t1 || t2 || t3 || t4 || t5 || t6 || t7
PHP then converts them into a compatible Python system description for Z3Prover SMT.
The data is wrapped in a cycle where the storage variables get index i, transaction variables index i + 1, and variables with expressions set the rules for the transition from the previous state to the next.
This is the very heart of our virtual machine, which provides a multi-transactional search engine.
fState: And( And( And( human[Steps] == 1 , wolf[Steps] == 1 ) , goat[Steps] == 1 ) , cabbage[Steps] == 1 )
final: fState[Steps]
fState:
wolf:
goat:
cabbage:
cabbageSide: Or( cabbage[i] == 0 , cabbage[i] == 1 )
goatSide: Or( goat[i] == 0 , goat[i] == 1 )
humanSide: Or( human[i] == 0 , human[i] == 1 )
t7: And( And( And( humanTravel[i] , wolf == wolf[i] ) , goat[i+1] == goat[i] ) , cabbage == cabbage[i] )
t3: And( And( And( humanTravel[i] , wolf == wolf[i] ) , goat[i+1] == goat[i] ) , cabbage == cabbage[i] + 1 )
t6: And( And( And( humanTravel[i] , wolf == wolf[i] ) , goat[i+1] == goat[i] ) , cabbage == cabbage[i] - 1 )
t2: And( And( And( humanTravel[i] , wolf == wolf[i] ) , goat[i+1] == goat[i] + 1 ) , cabbage == cabbage[i] )
t5: And( And( And( humanTravel[i] , wolf == wolf[i] ) , goat[i+1] == goat[i] - 1 ) , cabbage == cabbage[i] )
t1: And( And( And( humanTravel[i] , wolf == wolf[i] + 1 ) , goat[i+1] == goat[i] ) , cabbage == cabbage[i] )
t4: And( And( And( humanTravel[i] , wolf == wolf[i] - 1 ) , goat[i+1] == goat[i] ) , cabbage == cabbage[i] )
safeAlone: And( goat[i+1] != wolf , goat[i+1] != cabbage )
wolfSide: Or( wolf[i] == 0 , wolf[i] == 1 )
humanTravel: human[i] != human[i+1]
side: And( And( And( humanSide[i] , wolfSide[i] ) , goatSide[i] ) , cabbageSide[i] )
safe: Or( safeAlone[i] , goat[i+1] == human[i+1] )
objectTravel: Or( Or( Or( Or( Or( Or( t1[i] , t2[i] ) , t3[i] ) , t4[i] ) , t5[i] ) , t6[i] ) , t7[i] )
data: And( And( And( side[i] , safe[i] ) , humanTravel[i] ) , objectTravel[i] )
Conditions are sorted and inserted into a script template designed to describe the SMT system in python.
Blank template
import json
from z3 import *
s = Solver()
Steps=7
Num= Steps+1
$code$
#template, only start rest
s.add(data + start)
#template
s.add(final)
ind = 0
f = open("/var/www/html/all/bin/python/log.txt", "a")
while s.check() == sat:
ind = ind +1
print ind
m = s.model()
print m
print "traversing model..."
#for d in m.decls():
#print "%s = %s" % (d.name(), m[d])
f.write(str(m))
f.write("\n\n")
exit()
#s.add(Or(goat[0] != s.model()[data[0]] )) # prevent next model from using the same assignment as a previous model
print "Total solution number: "
print ind
f.close()
For the last state from the entire chain, the rules that are specified in the transfer transaction section apply.
So, Z3Prover will look for just such a set of conditions that will eventually allow you to withdraw funds from the contract.
As a result, we automatically get a fully working SMT model of our contract.
You can see that it is very similar to the model from my previous article, which I wrote manually.
Completed template
import json
from z3 import *
s = Solver()
Steps=7
Num= Steps+1
human = [ Int('human_%i' % (i + 1)) for i in range(Num) ]
wolf = [ Int('wolf_%i' % (i + 1)) for i in range(Num) ]
goat = [ Int('goat_%i' % (i + 1)) for i in range(Num) ]
cabbage = [ Int('cabbage_%i' % (i + 1)) for i in range(Num) ]
nothing= [ And( human[i] == human[i+1], wolf[i] == wolf[i+1], goat[i] == goat[i+1], cabbage[i] == cabbage[i+1] ) for i in range(Num-1) ]
start= [ human[0] == 1, wolf[0] == 0, goat[0] == 1, cabbage[0] == 0 ]
safeAlone= [ And( goat[i+1] != wolf[i+1] , goat[i+1] != cabbage[i+1] ) for i in range(Num-1) ]
safe= [ Or( safeAlone[i] , goat[i+1] == human[i+1] ) for i in range(Num-1) ]
humanTravel= [ human[i] != human[i+1] for i in range(Num-1) ]
cabbageSide= [ Or( cabbage[i] == 0 , cabbage[i] == 1 ) for i in range(Num-1) ]
goatSide= [ Or( goat[i] == 0 , goat[i] == 1 ) for i in range(Num-1) ]
humanSide= [ Or( human[i] == 0 , human[i] == 1 ) for i in range(Num-1) ]
t7= [ And( And( And( humanTravel[i] , wolf[i+1] == wolf[i] ) , goat[i+1] == goat[i] ) , cabbage[i+1] == cabbage[i] ) for i in range(Num-1) ]
t3= [ And( And( And( humanTravel[i] , wolf[i+1] == wolf[i] ) , goat[i+1] == goat[i] ) , cabbage[i+1] == cabbage[i] + 1 ) for i in range(Num-1) ]
t6= [ And( And( And( humanTravel[i] , wolf[i+1] == wolf[i] ) , goat[i+1] == goat[i] ) , cabbage[i+1] == cabbage[i] - 1 ) for i in range(Num-1) ]
t2= [ And( And( And( humanTravel[i] , wolf[i+1] == wolf[i] ) , goat[i+1] == goat[i] + 1 ) , cabbage[i+1] == cabbage[i] ) for i in range(Num-1) ]
t5= [ And( And( And( humanTravel[i] , wolf[i+1] == wolf[i] ) , goat[i+1] == goat[i] - 1 ) , cabbage[i+1] == cabbage[i] ) for i in range(Num-1) ]
t1= [ And( And( And( humanTravel[i] , wolf[i+1] == wolf[i] + 1 ) , goat[i+1] == goat[i] ) , cabbage[i+1] == cabbage[i] ) for i in range(Num-1) ]
t4= [ And( And( And( humanTravel[i] , wolf[i+1] == wolf[i] - 1 ) , goat[i+1] == goat[i] ) , cabbage[i+1] == cabbage[i] ) for i in range(Num-1) ]
wolfSide= [ Or( wolf[i] == 0 , wolf[i] == 1 ) for i in range(Num-1) ]
side= [ And( And( And( humanSide[i] , wolfSide[i] ) , goatSide[i] ) , cabbageSide[i] ) for i in range(Num-1) ]
objectTravel= [ Or( Or( Or( Or( Or( Or( t1[i] , t2[i] ) , t3[i] ) , t4[i] ) , t5[i] ) , t6[i] ) , t7[i] ) for i in range(Num-1) ]
data= [ Or( And( And( And( side[i] , safe[i] ) , humanTravel[i] ) , objectTravel[i] ) , nothing[i]) for i in range(Num-1) ]
fState= And( And( And( human[Steps] == 1 , wolf[Steps] == 1 ) , goat[Steps] == 1 ) , cabbage[Steps] == 1 )
final= fState
#template, only start rest
s.add(data + start)
#template
s.add(final)
ind = 0
f = open("/var/www/html/all/bin/python/log.txt", "a")
while s.check() == sat:
ind = ind +1
print ind
m = s.model()
print m
print "traversing model..."
#for d in m.decls():
#print "%s = %s" % (d.name(), m[d])
f.write(str(m))
f.write("\n\n")
exit()
#s.add(Or(goat[0] != s.model()[data[0]] )) # prevent next model from using the same assignment as a previous model
print "Total solution number: "
print ind
f.close()
After launch, Z3Prover solves a smart contract and displays a transaction chain to us, which will allow us to withdraw funds:
Winning transaction chain found:
Data transaction: human= 0, wolf= 0, goat= 1, cabbage= 0
Data transaction: human= 1, wolf= 0, goat= 1, cabbage= 1
Data transaction: human= 0, wolf= 0, goat= 0, cabbage= 1
Data transaction: human= 1, wolf= 1, goat= 0, cabbage= 1
Data transaction: human= 0, wolf= 1, goat= 0, cabbage= 1
Data transaction: human= 1, wolf= 1, goat= 1, cabbage= 1
Data transaction: human= 1, wolf= 1, goat= 1, cabbage= 1
Transfer transaction
In addition to the forwarding contract, you can experiment with your own contracts or try this simple example, which is solved in 2 transactions.
let contract = tx.sender
let a= extract(getInteger(contract,"a"))
let b= extract(getInteger(contract,"b"))
let c= extract(getInteger(contract,"c"))
let d= extract(getInteger(contract,"d"))
match tx {
case t:DataTransaction =>
let na= extract(getInteger(t.data,"a"))
let nb= extract(getInteger(t.data,"b"))
let nc= extract(getInteger(t.data,"c"))
let nd= extract(getInteger(t.data,"d"))
nd == 0 || a == 100 - 5
case s:TransferTransaction =>
( a + b - c ) * d == 12
case _ => true
}
Since this is the very first version, the syntax is very limited and bugs can occur.
In the following articles, I plan to highlight the further development of VM, and show how it is possible to create formally verified smart contracts with its help, and not just solve them.
A symbolic virtual machine is available at http://2.59.42.98/hyperbox/
Sources are available on github: http://github.com/scp1001/hyperbox
All VM logic is contained in 2 files, hyperbox.php and hyperbox2.php
