About the proximity of the peaks
“Before you comprehend this, it seems like a miracle. But after that there is nothing special. ”
No, not about the mountains, - about the counts. In mathematics, there are questions whose formulation is accessible to everyone, but the solution is nontrivial and without special preparation is difficult to explain. One of these problems can be briefly expressed as follows: how to correctly calculate distances in directed graphs? This somewhat abstract problem can be reduced to a very specific motivating task. It fits in one picture:
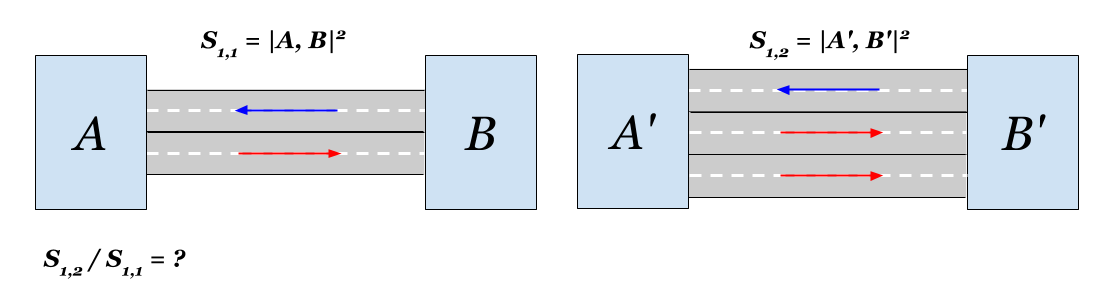
A small town is divided (for example, by a river, although in the context of the peaks the gorge is more suitable) into two districts (parts) and
and  . Communication between the districts is carried out along a single road (bridge), which has two lanes: to the side of
. Communication between the districts is carried out along a single road (bridge), which has two lanes: to the side of to
to  and back. In connection with population growth, the question arose of increasing the capacity of the road. Money as usual is barely enough and only enough for one lane in one direction. It is clear that even one lane will bring regions closer together, but the question is how much exactly? You are an urban
and back. In connection with population growth, the question arose of increasing the capacity of the road. Money as usual is barely enough and only enough for one lane in one direction. It is clear that even one lane will bring regions closer together, but the question is how much exactly? You are an urban crazy mathematician, and it was you who were invited in order to receive a reasonable answer.
Instead ofKonigsberg bridges, a slightly more rigorous graph theory language can be used. So, there is a directed graph with two vertices (nodes) and
and  . The magnitude of the connection (conductivity, bandwidth) in the forward and reverse direction are initially equal. The question is how much will the distance between the nodes change if the conductivity in one of the directions is doubled?
. The magnitude of the connection (conductivity, bandwidth) in the forward and reverse direction are initially equal. The question is how much will the distance between the nodes change if the conductivity in one of the directions is doubled?
And yes, if you are a real mathematicianwelder , you can offer (and justify) a solution for any direct and feedback values. Ideally, for a graph with any number of nodes and links.
It is clear that the usual (kilometer) distance between regions does not depend on the presence or absence of the road. Therefore, it does not fit here - we need to rely on communication. The more districts are connected - the closer they are - the more residents can get to another area per unit of time.
To assess the measure of proximity between nodes of an undirected graph, the so-called resistive distance can be used . Earlier, we already described the properties of this distance on the habr in several articles .
The resistive distance is equivalent to the concept of effective resistance, when it comes to the electrical network. Therefore, in electric language, the problem can be formulated as follows. Between two nodes, two diodes of equal conductivities are counterclockwise connected. How will the resistance between these points change if you add another diode? (I apologize if the electric language failed and I wrote nonsense here).
Also, effective resistance can be interpreted in the Markov language for the probabilities ofdrunk random walks (for those wishing to delve into the topic - google “Random walks and electric networks”).
The resistive distance is quadratic, - corresponds to the square of the linear distance. Quadratic distances are also called quadrans.. But since other (linear) distances are not used in this problem, we do not need the term quadrans here. (There is enough bird’s tongue even without it).
In general, the term "resistive distance" also does not look good. He implies that we are talking about some kind of unusual distance unknown to science. In fact, the resistive distance is the usual Euclidean distance . But in the affine space. We use this feature of it further.
If we know what a "resistive distance" is, then why can't we "just take and calculate it" for a given graph?
Hm. In principle, easy. If we are talking about an undirected graph. If the city had built strips in both directions, then the resistive distance would have decreased by exactly half. Since the resistance is inversely proportional to conductivity, and conductivity (throughput) has doubled. And if I added two bands in each direction, then the distance would decrease by 3 times. Everything is quite trivial here. (And probably, someone here can already guess the general form of the solution. And we go further).
When the opposing relationships are not equal, then everything gets complicated. And quite severely.
(This is my thesis - maybe someone can convince me). “No” - here means that it is not in the textbooks, wiki, and in the heads (more precisely - there are many different ways from different authors that require different assumptions and definitions). There is a way (though not so simple). In this article, we are just describing it.
The very determination of the distance in the presence of directed connections requires clarification if we are talking about a directed graph (non-commutative metric, I apologize). You can talk about the distance from before
before  , but you can from
, but you can from  before
before  . And most likely these distances are not always equal. What kind of distances are we talking about in the problem?
. And most likely these distances are not always equal. What kind of distances are we talking about in the problem?
We will emerge and take a deep breath. We have already mentioned that the resistive distance is the usual Euclidean. This means that its definition can be reduced to the definition of Euclidean distance as the norm of the difference of two elements:

This definition does not depend on the order of the elements - this is the commutative distance, proximity (more precisely, the distance) of the elements. A point in an expression means a scalar product operation (metric space). Accordingly, expression (1) can be disclosed:

Here ,
,  - norms of elements. When it comes to graphs, then the norms of the elements are usually zero. In the original problem nothing is said about the norms, so you can take them to be zero (more about what the norms of elements in the affine space mean . Here , and even more details, here ). Then the expression for the desired distance takes the form:
- norms of elements. When it comes to graphs, then the norms of the elements are usually zero. In the original problem nothing is said about the norms, so you can take them to be zero (more about what the norms of elements in the affine space mean . Here , and even more details, here ). Then the expression for the desired distance takes the form:

According to expression (3), all that is needed to solve the problem is to find the scalar products of elements (nodes) in a directed graph (it’s easy to say, but how to do this?).
Along the way, formula (3) shows that our general (commutative) measure of proximity between elements and
and  is the sum of two directed distances:
is the sum of two directed distances:
 - directional distance from
- directional distance from  before
before  ,
,
 - directional distance from
- directional distance from  before
before  .
.
The rumble subsided. The fun is over. Then come the dull details of the description of the essence of the method for calculating the scalar product between nodes of a directed graph. This is the part that I don’t know how to say “in a simple way on the fingers”. But this is where the most important thing in the article. Something worth wasting time on it.
The general line of reasoning is as follows. We carefully and withoutemotions of new additional assumptions transfer the known properties of the metric of symmetric spaces to asymmetric ones. All that is needed is to take into account the peculiarities of the metric in affine spaces.
Any connected graph (whether directed or not) defines an affine metric space. Some properties of such spaces in symmetric (commutative) execution were (chaotically) described in the already mentioned series of articles or more precisely and in detail in the mentioned longrid . Do not rush to switch - below we give (though, by the tongue twister) the main squeezes.
What is important. Well-known first.
1. The affinity of space means that the concepts of vector and element in space are different. Vector is the difference of elements. This seemingly insignificant feature leads to significant consequences if a metric is defined in space.
2. The space is defined by a basis consisting of elements. The vertices of the graph are the basis of space. Relationships in a graph determine its metric properties.
3. A graph connectivity characteristic is the adjacency matrix . But for metric (and other) properties, the Laplacian of the graph (Kirchhoff matrix) is more important .
.
4. The Laplacian of a graph is an almost metric tensor. “Almost” - here means that it is incomplete. Laplacian is a degenerate matrix and therefore not invertible. And the standard metric tensor is completely reversible.
Now less known.
5. The difference between elements and vectors in a metric affine space leads to the existence of a null vector in it . The scalar product of elements with a null vector in a commutative (symmetric) space is equal to unity (in a non-commutative space it depends on the direction of multiplication). Without a zero vector, the graph space is not complete! It is important.
. The scalar product of elements with a null vector in a commutative (symmetric) space is equal to unity (in a non-commutative space it depends on the direction of multiplication). Without a zero vector, the graph space is not complete! It is important.
6. The orthogonal center of the basis is dual with respect to the null vector. . This is such an element that is orthogonal to all other elements of the basis (except for the zero-vector). Recall that the orthogonality of elements means that their scalar product is zero. The orthocenter of a triangle is the circumscribed circle . Yes, in a full affine space an element with a nonzero norm is not a point, but an n-dimensional sphere.
. This is such an element that is orthogonal to all other elements of the basis (except for the zero-vector). Recall that the orthogonality of elements means that their scalar product is zero. The orthocenter of a triangle is the circumscribed circle . Yes, in a full affine space an element with a nonzero norm is not a point, but an n-dimensional sphere.
7. The Laplacian of the graph, together with the coordinates of the orthogonal center, becomes complete (a full-fledged metric tensor). In other words, full Laplacian Is an ordinary count laplacian
Is an ordinary count laplacian  but bordered by the barycentric coordinates of the orthogonal center.
but bordered by the barycentric coordinates of the orthogonal center.
8. Inversion of the full Laplacian allows one to obtain a complete Gramian - the matrix of scalar products of the elements of the basis (in our case, the vertices of the graph). This gramian is also a full-fledged metric tensor of space.
- the matrix of scalar products of the elements of the basis (in our case, the vertices of the graph). This gramian is also a full-fledged metric tensor of space.
9. The framing of a full gramian is a tuple of units (scalar products of basis elements and a zero-vector). In the corner - zero, this is the norm of the zero-vector itself.
The famous Cayley-Menger matrix is an almost regular Gramian.
As a result, we conclude that, according to claim 8, the problem of determining scalar products (and, therefore, distances) between the nodes of the graph is reduced to determining the initial metric tensor of the basis .
.
In the case of symmetrical bonds, the construction of a complete Gramian from the Laplacian (and vice versa) does not cause any particular difficulties. In this case, the scalar products of the elements of the basis and the zero-vector are commutative - they do not depend on the order of multiplication:

For directed graphs (non-commutative spaces) the problem is complicated. If only because the very number of possible connections in the directed graph doubles.
About the properties of the Laplacian of the directed graph, we also already wrote on the Habr . They told how to use the potentials of the Laplacian to rank objects. In terms of bases, the potentials of the Laplacian are the dual coordinates of the zero-vector (annihilator of the Laplacian).
In this article, we are interested in metric properties. If the graph is directed, then the scalar product between its vertices depends on the order:

This means that the dual coordinates in the directed graphs are split (into left and right). The values of the scalar products of the zero-vector and the elements of the basis (bordering the gramian) also depend on the order of the factors. And therefore, in contrast to the commutative space, here one half of the dual coordinates of the zero-vector is unknown and must be determined.

However, there are many known quantities.
Firstly, the Laplacian himself is known. In addition, it is known that the sum of its rows is zero (in the general case, this is an optional requirement, but for Laplacians of directed graphs this is usually the case). It is also important that the barycentric coordinates of the elements are unique, since they are independent of the space metric. That is, the bordering of the Laplacian of the graph is symmetrical for both the directed and the undirected graph (I did not immediately recognize this point). Finally, we know the norms of the elements of the basis (usually in the graphs they are equal to zero).
It remains to substitute all the known and unknown in the identity connecting the Laplacian and Gramian:

Here Is an identity matrix. In this identity, the meaning of the transition from an incomplete Laplacian to a complete one.
Is an identity matrix. In this identity, the meaning of the transition from an incomplete Laplacian to a complete one.
Let's move from words to deeds. This is what the Laplacian looks like for a graph of two nodes:
for a graph of two nodes:

For simplicity, we have designated the relationship with numbers: . It is assumed that the values of the bonds are known - through them we will express all other quantities.
. It is assumed that the values of the bonds are known - through them we will express all other quantities.
Full Laplacian includes the coordinates of the orthocenter
includes the coordinates of the orthocenter ![$ [rz, az, bz] $](https://habrastorage.org/getpro/habr/formulas/a47/48c/31f/a4748c31f7622cb053e74973731dcedd.svg) :
:

Here - the norm of the orthocenter (in the symmetric case is interpreted as the square of the radius),
- the norm of the orthocenter (in the symmetric case is interpreted as the square of the radius),  and
and  - coefficients of the decomposition of the orthocenter on the basis
- coefficients of the decomposition of the orthocenter on the basis  (barycentric weights).
(barycentric weights).
Full gramian It looks something like this:
It looks something like this:

Here are the tuples![$ [za, zb] $](https://habrastorage.org/getpro/habr/formulas/741/e49/ad9/741e49ad9734c98dddcd9fb916df791f.svg) and
and ![$ [1, 1] $](https://habrastorage.org/getpro/habr/formulas/332/1ba/f34/3321baf34f970c1554598d032a8a10b6.svg) reflect the dual coordinates of the null vector. These coordinates are annihilators of the Laplacian (when multiplied by the Laplacian they give a zero vector - not to be confused with a zero vector!).
reflect the dual coordinates of the null vector. These coordinates are annihilators of the Laplacian (when multiplied by the Laplacian they give a zero vector - not to be confused with a zero vector!).
To solve the problem, we need to find the sum of the values of the gramian: .
.
We consider the number of unknowns: - only 7 (yes, yes - to find out the value of one unfortunate distance, we need to calculate seven more additional values). There are two well-known connections at the entrance -
- only 7 (yes, yes - to find out the value of one unfortunate distance, we need to calculate seven more additional values). There are two well-known connections at the entrance - and
and  . Identity
. Identity will give 9 equations. Total 7 + 2 = 9, - everything converges (surprisingly). It remains to simply solve the system of equations.
will give 9 equations. Total 7 + 2 = 9, - everything converges (surprisingly). It remains to simply solve the system of equations.
For a graph of two nodes, the solution (all unknowns) can be expressed in explicit form. We give finite expressions for the quantities of interest to us. We introduce the concept of general geometric connectivity - this is the reciprocal of the norm of the orthogonal center . Its dimension coincides with the dimension of the graph links. For a graph of two nodes (and two connections), the geometric connection has a nice expression:
. Its dimension coincides with the dimension of the graph links. For a graph of two nodes (and two connections), the geometric connection has a nice expression:

Through this connection, one can express scalar products of nodes:

You can translate scalar products in directional distances
in directional distances  (3):
(3):

The desired commutative distance between nodes is determined by the sum:

At last. Expression (4) - this is the desired formula.
You can load the school textbook with another useless formula.
If the connections are equal, then the result coincides with the resistive distance in the undirected graphs:

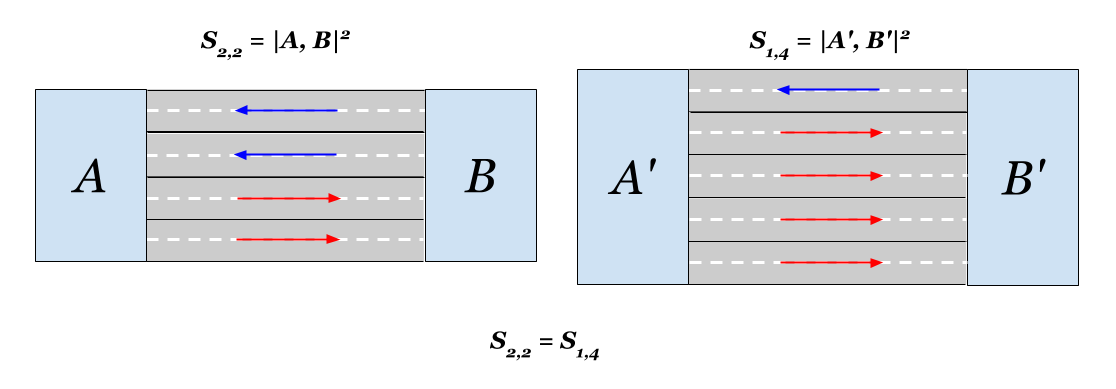
We will calculate what is there with our town. If you lay a second lane, then communication in one direction will double. Accordingly, the new distance can be expressed in terms of the original:
can be expressed in terms of the original:

The distance between the areas will decrease in time. It was obvious, right?
time. It was obvious, right?
It also turns out that in terms of distance, adding one lane to each two-lane road on each side is equivalent to adding three lanes on one side. Euclidean proximity in both cases will double. Interesting.
That's all. Thank you for your attention).
No, not about the mountains, - about the counts. In mathematics, there are questions whose formulation is accessible to everyone, but the solution is nontrivial and without special preparation is difficult to explain. One of these problems can be briefly expressed as follows: how to correctly calculate distances in directed graphs? This somewhat abstract problem can be reduced to a very specific motivating task. It fits in one picture:

1. Statement of the problem. I live on one, but you on the other.
A small town is divided (for example, by a river, although in the context of the peaks the gorge is more suitable) into two districts (parts)
How much closer are the areas if you build another strip in one direction?
Wording for advanced
Instead of
And yes, if you are a real mathematician
The answer for those in a hurry
Yes, I was going to give a quick answer here, but changed my mind. Why deprive the reader of the pleasure of self-reflection? Perhaps you suggest something more worthwhile than the author. In any case, you can immediately scroll to the end of the article. Sorry).
Intimacy and drunken wanderings
It is clear that the usual (kilometer) distance between regions does not depend on the presence or absence of the road. Therefore, it does not fit here - we need to rely on communication. The more districts are connected - the closer they are - the more residents can get to another area per unit of time.
To assess the measure of proximity between nodes of an undirected graph, the so-called resistive distance can be used . Earlier, we already described the properties of this distance on the habr in several articles .
The resistive distance is equivalent to the concept of effective resistance, when it comes to the electrical network. Therefore, in electric language, the problem can be formulated as follows. Between two nodes, two diodes of equal conductivities are counterclockwise connected. How will the resistance between these points change if you add another diode? (I apologize if the electric language failed and I wrote nonsense here).
Also, effective resistance can be interpreted in the Markov language for the probabilities of
The resistive distance is quadratic, - corresponds to the square of the linear distance. Quadratic distances are also called quadrans.. But since other (linear) distances are not used in this problem, we do not need the term quadrans here. (There is enough bird’s tongue even without it).
In general, the term "resistive distance" also does not look good. He implies that we are talking about some kind of unusual distance unknown to science. In fact, the resistive distance is the usual Euclidean distance . But in the affine space. We use this feature of it further.
And what, in fact, is the problem?
If we know what a "resistive distance" is, then why can't we "just take and calculate it" for a given graph?
Hm. In principle, easy. If we are talking about an undirected graph. If the city had built strips in both directions, then the resistive distance would have decreased by exactly half. Since the resistance is inversely proportional to conductivity, and conductivity (throughput) has doubled. And if I added two bands in each direction, then the distance would decrease by 3 times. Everything is quite trivial here. (And probably, someone here can already guess the general form of the solution. And we go further).
When the opposing relationships are not equal, then everything gets complicated. And quite severely.
There is no simplelegalgenerally accepted way to determine the proximity of peaks (resistive distances) in a directional graph .
(This is my thesis - maybe someone can convince me). “No” - here means that it is not in the textbooks, wiki, and in the heads (more precisely - there are many different ways from different authors that require different assumptions and definitions). There is a way (though not so simple). In this article, we are just describing it.
The very determination of the distance in the presence of directed connections requires clarification if we are talking about a directed graph (non-commutative metric, I apologize). You can talk about the distance from
Euclidean distance rules
We will emerge and take a deep breath. We have already mentioned that the resistive distance is the usual Euclidean. This means that its definition can be reduced to the definition of Euclidean distance as the norm of the difference of two elements:
This definition does not depend on the order of the elements - this is the commutative distance, proximity (more precisely, the distance) of the elements. A point in an expression means a scalar product operation (metric space). Accordingly, expression (1) can be disclosed:
Here
According to expression (3), all that is needed to solve the problem is to find the scalar products of elements (nodes) in a directed graph (it’s easy to say, but how to do this?).
Along the way, formula (3) shows that our general (commutative) measure of proximity between elements
2. The decision. Long road in the dunes
The general line of reasoning is as follows. We carefully and without
Any connected graph (whether directed or not) defines an affine metric space. Some properties of such spaces in symmetric (commutative) execution were (chaotically) described in the already mentioned series of articles or more precisely and in detail in the mentioned longrid . Do not rush to switch - below we give (though, by the tongue twister) the main squeezes.
Affine metric space (undirected graph)
What is important. Well-known first.
1. The affinity of space means that the concepts of vector and element in space are different. Vector is the difference of elements. This seemingly insignificant feature leads to significant consequences if a metric is defined in space.
2. The space is defined by a basis consisting of elements. The vertices of the graph are the basis of space. Relationships in a graph determine its metric properties.
3. A graph connectivity characteristic is the adjacency matrix . But for metric (and other) properties, the Laplacian of the graph (Kirchhoff matrix) is more important
4. The Laplacian of a graph is an almost metric tensor. “Almost” - here means that it is incomplete. Laplacian is a degenerate matrix and therefore not invertible. And the standard metric tensor is completely reversible.
Now less known.
5. The difference between elements and vectors in a metric affine space leads to the existence of a null vector in it
6. The orthogonal center of the basis is dual with respect to the null vector.
7. The Laplacian of the graph, together with the coordinates of the orthogonal center, becomes complete (a full-fledged metric tensor). In other words, full Laplacian
8. Inversion of the full Laplacian allows one to obtain a complete Gramian
9. The framing of a full gramian is a tuple of units (scalar products of basis elements and a zero-vector). In the corner - zero, this is the norm of the zero-vector itself.
The famous Cayley-Menger matrix is an almost regular Gramian.
As a result, we conclude that, according to claim 8, the problem of determining scalar products (and, therefore, distances) between the nodes of the graph is reduced to determining the initial metric tensor of the basis
We need a method for constructing a full gramian graphfor a given (incomplete) Laplacian
.
In the case of symmetrical bonds, the construction of a complete Gramian from the Laplacian (and vice versa) does not cause any particular difficulties. In this case, the scalar products of the elements of the basis and the zero-vector are commutative - they do not depend on the order of multiplication:
For directed graphs (non-commutative spaces) the problem is complicated. If only because the very number of possible connections in the directed graph doubles.
Non-commutative affine space (directed graph)
About the properties of the Laplacian of the directed graph, we also already wrote on the Habr . They told how to use the potentials of the Laplacian to rank objects. In terms of bases, the potentials of the Laplacian are the dual coordinates of the zero-vector (annihilator of the Laplacian).
In this article, we are interested in metric properties. If the graph is directed, then the scalar product between its vertices depends on the order:
This means that the dual coordinates in the directed graphs are split (into left and right). The values of the scalar products of the zero-vector and the elements of the basis (bordering the gramian) also depend on the order of the factors. And therefore, in contrast to the commutative space, here one half of the dual coordinates of the zero-vector is unknown and must be determined.
However, there are many known quantities.
Firstly, the Laplacian himself is known. In addition, it is known that the sum of its rows is zero (in the general case, this is an optional requirement, but for Laplacians of directed graphs this is usually the case). It is also important that the barycentric coordinates of the elements are unique, since they are independent of the space metric. That is, the bordering of the Laplacian of the graph is symmetrical for both the directed and the undirected graph (I did not immediately recognize this point). Finally, we know the norms of the elements of the basis (usually in the graphs they are equal to zero).
It remains to substitute all the known and unknown in the identity connecting the Laplacian and Gramian:
Here
Shut up and believe
Let's move from words to deeds. This is what the Laplacian looks like
For simplicity, we have designated the relationship with numbers:
Full Laplacian
Here
Full gramian
Here are the tuples
To solve the problem, we need to find the sum of the values of the gramian:
We consider the number of unknowns:
For a graph of two nodes, the solution (all unknowns) can be expressed in explicit form. We give finite expressions for the quantities of interest to us. We introduce the concept of general geometric connectivity - this is the reciprocal of the norm of the orthogonal center
Through this connection, one can express scalar products of nodes:
You can translate scalar products
The desired commutative distance between nodes is determined by the sum:
Grandma has arrived
At last. Expression (4) - this is the desired formula.
The distance between the vertices of the graph of two nodes is inversely proportional to the square root of the product of the counter-links.
You can load the school textbook with another useless formula.
If the connections are equal, then the result coincides with the resistive distance in the undirected graphs:
We will calculate what is there with our town. If you lay a second lane, then communication in one direction will double. Accordingly, the new distance
The distance between the areas will decrease in
It also turns out that in terms of distance, adding one lane to each two-lane road on each side is equivalent to adding three lanes on one side. Euclidean proximity in both cases will double. Interesting.

That's all. Thank you for your attention).
Application. Explicit expressions for the remaining elements of the matrices of our graph
Coordinates of the orthocenter:

Scalar products of a basis and a null vector (annihilator of the Laplacian):

Scalar products of a basis and a null vector (annihilator of the Laplacian):
