ALU with 12 transistors (actually not)

What can be done with 12 transistors? If the circuit is analog, it can be, for example, a radio or amplifier with decent characteristics. For a digital circuit, this is disastrously small. Even in such a simple chip as ALU K155IP3 (74181), there are much more of them.

In fact, there are not 12, but 27 transistors here, but only 11 of them are used in the ALU itself (the twelfth transistor, forcing a logic zero to the transfer input when choosing logical operations, is not installed). The remaining transistors are involved in the shaper of signals supplied to the inputs of the ALU. When the ALU is included in the transistor processor, the former may not be needed if all the necessary signals are already generated there.

How to keep within this amount? Firstly, make ALU one-bit, secondly, reduce the number of operations to two arithmetic and five logical (K155IP3 and each of them have 16, but there are actually more of them here), thirdly ...

... perform ALU by unusual DCTL technology (direct coupled transistor logic), which can significantly reduce the number of components.

The simulation was performed in Falstad , this simulator is convenient in that it shows the direction of current flow in the form of "running lights". Files: only full adder and ready ALU .

To begin with, we will build "ALU" with one function - a full adder. Let's break the scheme into two halves. The first is designed to prepare input signals for the adder:



The switches can be used to set two single-bit numbers - A and B and the transfer signal. Of these, the circuit generates four signals (the fourth is the same B, only inverted).

The second half of the circuit is the adder itself:



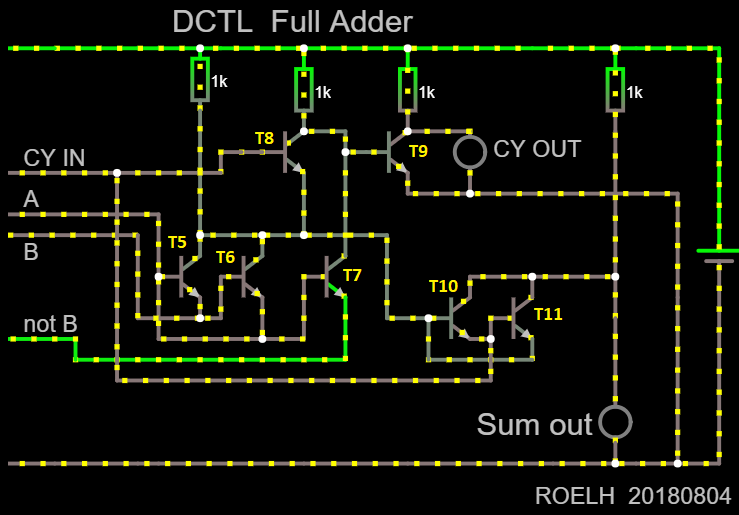
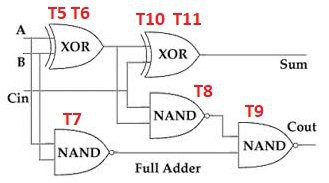
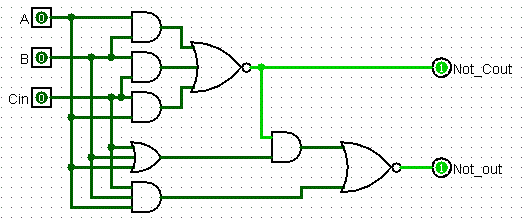
it is an implementation of the classic full adder. The structural diagram additionally shows the distribution of transistors by logical elements:



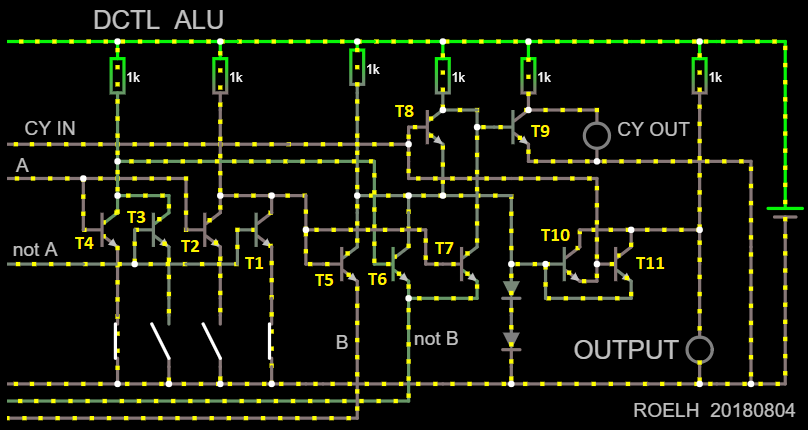
In order to turn all this into a multifunctional ALU, we first redo the input signal conditioner in such a way that it generates in direct and inverted form not only the value of B, but also the value of A:



But since the author plans to use his ALU as a part of the processor on discrete components, such a shaper may not be needed: there both quantities will be in direct and inverted form. Therefore, the transistors of the shaper are not included in the number of transistors ALU. Yes, and without a processor, you can just take the switches with cross over contacts. Well, now - actually ALU:



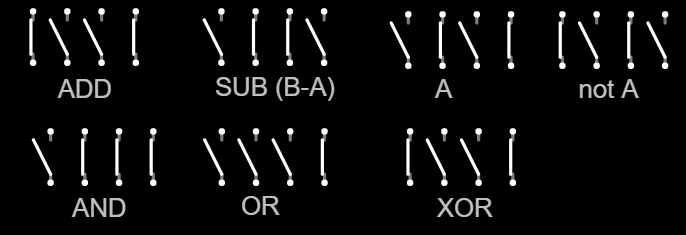
With four switches you can select the function performed by ALU. Only 7 basic ones are shown below:



In order for the ALU not to be “spherical in a vacuum”, but to receive signals from outside, the switches must be replaced with transistors. Since there is no transistor to force a logical zero to the transfer input when selecting logical functions, it is necessary to manually apply zero to this input in such cases.

Although the figure shows only 7 functions, you can try all 16 combinations of switch positions. In particular, the functions AND-NOT, OR-NOT, EXCLUSIVE OR-NOT, transmission of signal B through and through, inversion of the same signal will be obtained.

Simulation can bring surprises. Do you know that a bipolar transistor can work when passing current through it in the opposite direction? This happens with some combinations of input signals. In an analog amplifier, the gain is reduced, but the logic circuits continue to work in the same way as in normal mode.

The supply voltage is +5 V. In the simulator, transistors of general application NPN structure are selected.

The adder is obtained with through transfer. The transfer signal has to go through transistors T8 and T9. If this is too slow, you must first check how the circuit connected to the emitter of the T8 transistor affects the operation of the circuit. Transfer can also be done faster if you execute it for two bits at the same time.

If only a full adder is needed, then conventional diode-transistor logic (DTL) is also suitable. You only need two transistors, but diodes ... You can replace these transistors with lamps, you get what the author calls DVTL - diode-vacuum-tube-logic.



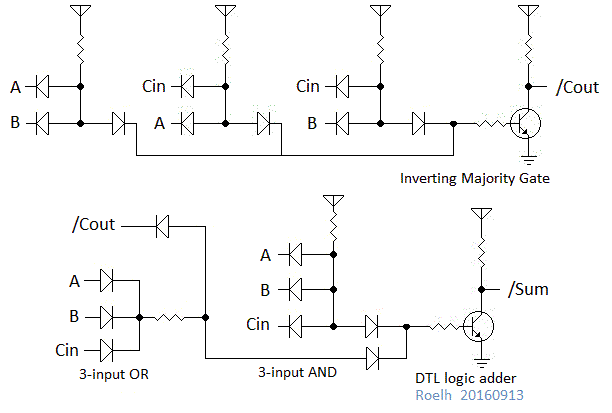
The top of the circuit generates an inverted transfer signal. The second calculates the inverted sum: AMOUNT = ((A or B or C in) and / C out). This expression can also be represented as (A and B and C in).

The block diagram is as follows:



By adding a few more components, you can force zero or one to the transfer input. Then the circuit will be able to perform the AND operation (one at the transfer input, zero at the inverted transfer output), and also OR (zero at the transfer input, one at the inverted transfer output).

To send a signal “inverted C o” to the input “C in” of the circuit for the next bit, you need a transistor inverter. Or you can accept the rule according to which direct and inverse logic alternates between bits.

All this can be turned into a valid ALU by calculating the resistors and adding additional components to optimize the "responsiveness" of the circuit. Devices connected to the inputs must contain keys that close them to the ground (for the inputs of the diode “AND”), or connect them to the power plus (for the inputs of the diode “OR”).

This is a very simple scheme, it does not implement fast transfer.