Information Entropy of Chaos
- Tutorial

Introduction
There are a lot of publications on Habr in which the concept of entropy is considered, here are just a few of them [1 ÷ 5]. The publications were positively received by readers and aroused great interest. It is enough to give the definition of entropy given by the author of the publication [1]: “entropy is how much information you do not know about the system.” Publications about the chaos phenomenon on Habr are also sufficient [6–9]. However, the relationship of entropy and chaos in both groups of publications was not considered.
This is due to the fact that different areas of knowledge distinguish different types of measures of chaos:
- informational;
- thermodynamic;
- differential;
- cultural.
Chaos measures are also described taking into account their specificity, even in one of these areas is quite difficult.
Trying to simplify the task as much as possible, I decided to consider the relationship between informational entropy and chaos using the example of the similarity of the regions of passage from order to chaos in the diagrams in the form of point mappings and in the graphs of the entropy coefficient for these regions.
What came of this you will learn by looking under the cat.
The mechanisms of transition from order to chaos
An analysis of the mechanisms of the transition from order to chaos in real systems and various models has revealed the versatility of relatively few scenarios of transition to chaos. The transition to chaos can be represented in the form of a bifurcation diagram (the term “bifurcation” is used to denote qualitative rearrangements of the system with the emergence of a new mode of its behavior).
The entry of the system into unpredictable mode is described by a cascade of bifurcations following one after another. The cascade of bifurcations leads sequentially to a choice between two solutions, then four and so on, the system begins to oscillate in a chaotic, turbulent mode of sequentially doubling the number of possible values.
We consider bifurcations of period doubling and the appearance of chaos in point mappings. Display is a function that shows the dependence of the following values of the system parameters on previous values:
Consider also the second commonly used function:
Using point mappings, objects are studied not with continuous, but with discrete time . Upon transition to the display, the dimension of the system under study may decrease.
When changing the external parameter \ lambda, point mappings exhibit rather complicated behavior, which becomes chaotic with sufficiently large \ lambda. Chaos is a very fast recession of trajectories in phase space.
Bifurcation is a qualitative restructuring of the motion picture. The values of the control parameter at which bifurcations occur are called critical or bifurcation values.
To build the diagrams, we will use the following two listings:
No. 1. For function:
Program listing
# -*- coding: utf8 -*-
import matplotlib.pyplot as plt
from numpy import *
def f(a,x0):
x1=(a-1)/a#точка пересечения функции с прямой
def ff(x):#логистическая функция
return a*x*(1-x)
def fl(x):
return x
x=x0;y=0;Y=[];X=[]
for i in arange(1,1000,1):
X.append(x)
Y.append(y)
y=ff(x)
X.append(x)
Y.append(y)
x=y
plt.title('Диаграмма логистической функции \n\
$x_{n+1}=\lambda \cdot x_{n}\cdot (1-x_{n})$ при $\lambda$ =%s и x0=%s '%(a,x0))
plt.plot(X,Y,'r')
x1=arange(0,1,0.001)
y1=[ff(x) for x in x1]
y2=[fl(x) for x in x1]
plt.plot(x1,y1,'b')
plt.plot(x1,y2,'g')
plt.grid(True)
plt.show()
No. 2. For function
Program listing
# -*- coding: utf8 -*-
import matplotlib.pyplot as plt
from numpy import *
def f(a,x0):
x1=((a-1)/a)**0.5
def ff(x):#логистическая функция
return a*x*(1-x**2)
def fl(x):
return x
x=x0;y=0;Y=[];X=[]
for i in arange(1,1000,1):
X.append(x)
Y.append(y)
y=ff(x)
X.append(x)
Y.append(y)
x=y
plt.title('Диаграмма логистической функции \n\
$x_{n+1}=\lambda \cdot x_{n}\cdot (1-x_{n}^{2})$ при $\lambda$ =%s и x0=%s '%(a,x0))
plt.plot(X,Y,'r')
x1=arange(0,1,0.001)
y1=[ff(x) for x in x1]
y2=[fl(x) for x in x1]
plt.plot(x1,y1,'b')
plt.plot(x1,y2,'g')
plt.grid(True)
plt.show()
To assess the impact of the nature of the logistic function on critical values
For 0 <\ lambda <1 for
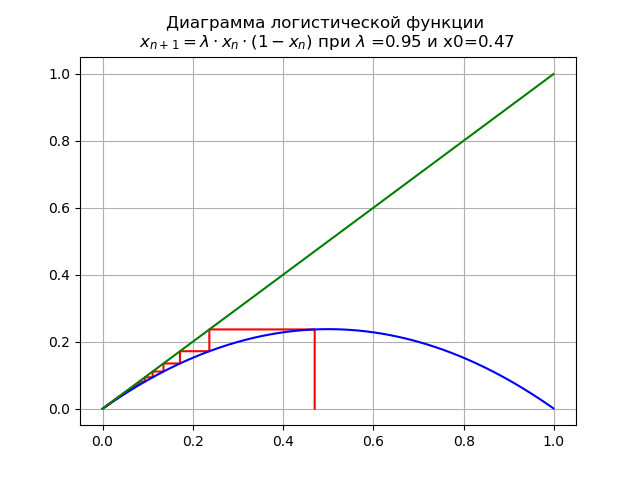
In this case, the map has a single fixed point
which is sustainable.
At
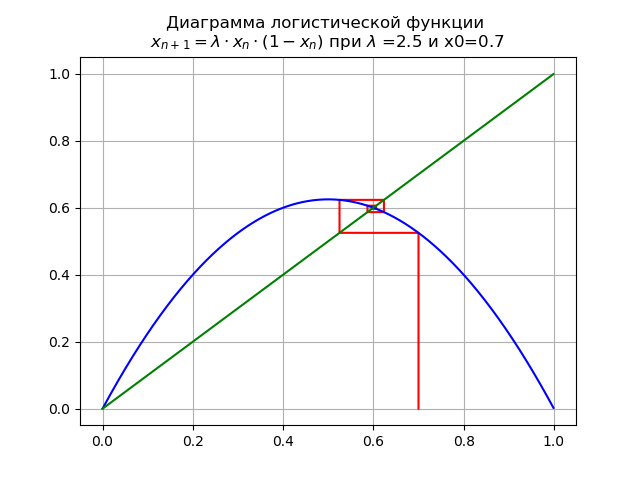
On the interval [0, 1], one more fixed stable point appears
At
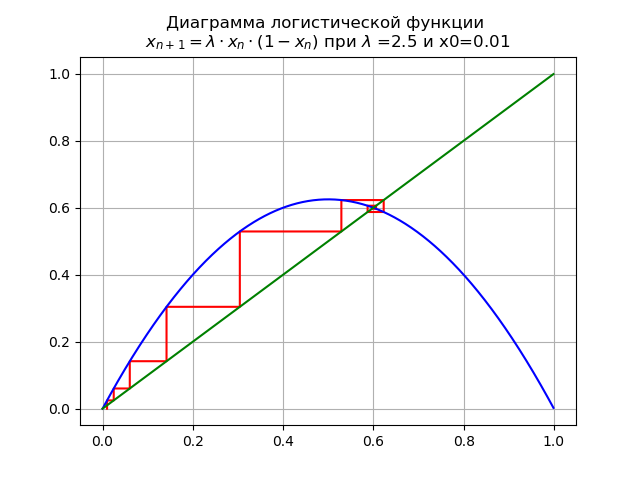
Fixed point
At
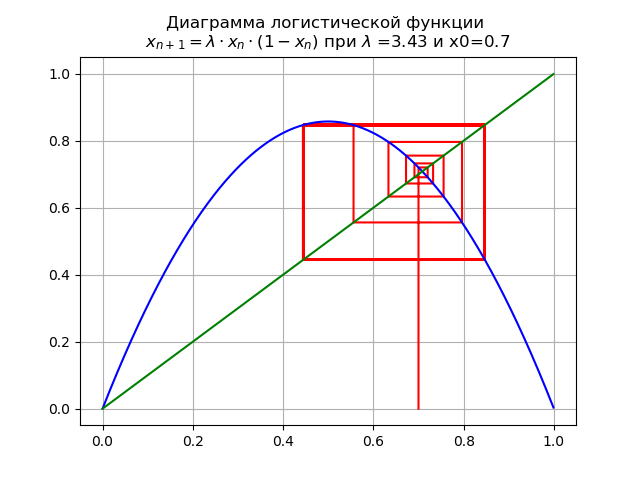
mapping undergoes bifurcation: a fixed point
At
and x0 = 0.2 we get the diagram:
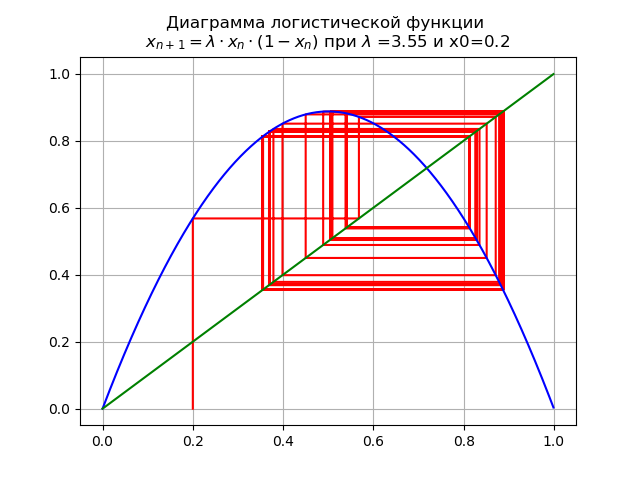
When passing the parameter
At the final value
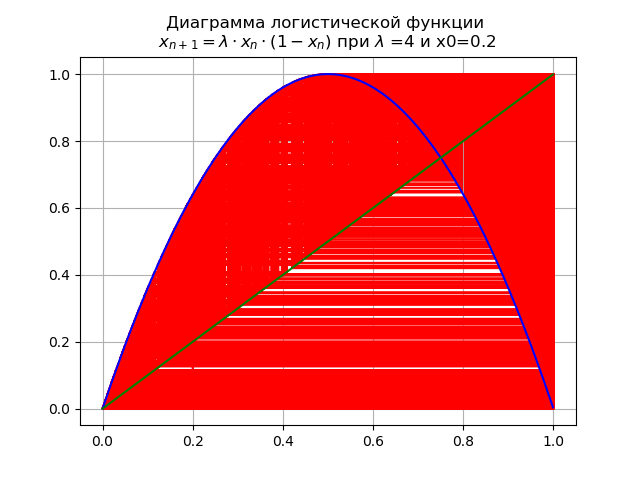
To assess the influence of the nature of the logistic function on critical values
At

map has a single fixed point
At
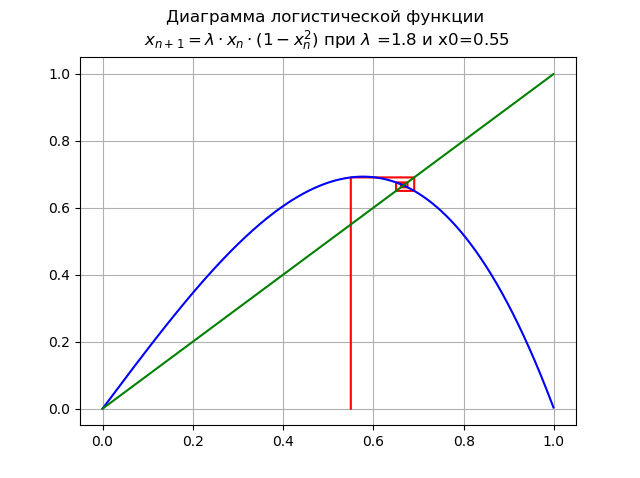
Point
At
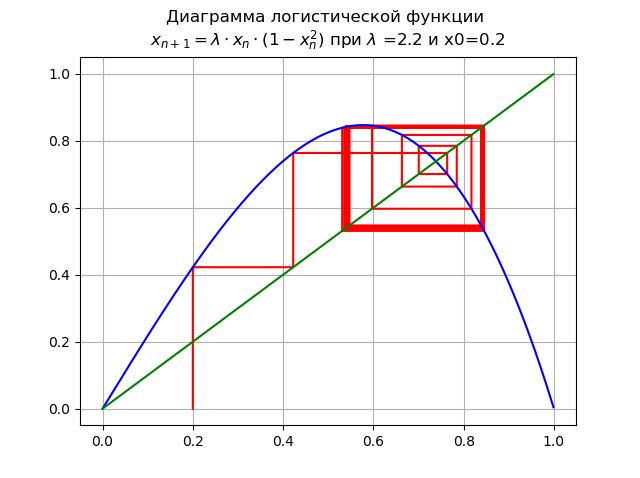
A period doubling bifurcation occurs, a 2-fold cycle appears. Further increase
At
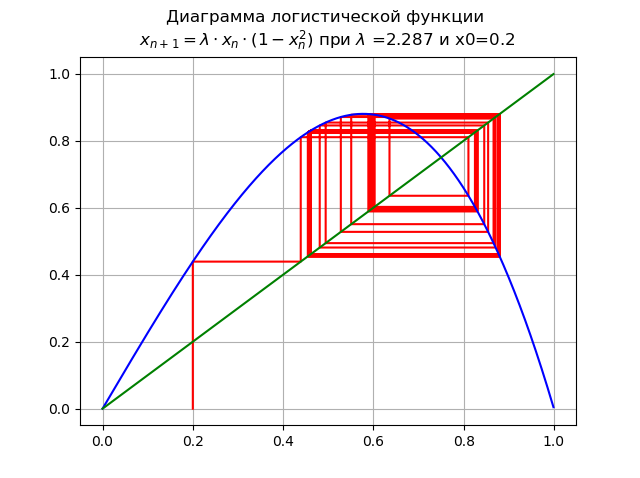
Increase
At

As was shown in the diagrams, with an increase in the order of the logistic function, the range of change
Using diagrams, we traced the path from order to chaos, while setting the values
- entropy is a measure of chaos. This answer can be fully attributed to information chaos, however, what entropy is applied here and how to compare with the numerical value already considered
Information entropy and entropy coefficient
We will consider information binary entropy for independent random events.
This value is also called the mean entropy of the message. Value
We will use decimal logarithms in which entropy and information are measured in bits. The amount of information in bits will be calculated correctly when, for example, variables
where X and
An estimate of the entropy value of a random variable from experimental data is found from a histogram from the following relation:
Where:
The entropy coefficient is determined from the ratio:
Where:
Information entropy as a measure of chaos
To analyze the phenomena of information chaos using the entropy coefficient, we first create a branch diagram for the function
Branch diagram
import matplotlib.pyplot as plt
import matplotlib.pyplot as plt
from numpy import*
N=1000
y=[]
y.append(0.5)
for r in arange(3.58,3.9,0.0001):
for n in arange(1,N,1):
y.append(round(r*y[n-1]*(1-y[n-1]),4))
y=y[N-250:N]
x=[r ]*250
plt.plot( x,y, color='black', linestyle=' ', marker='.', markersize=1)
plt.figure(1)
plt.title("Диаграмма ветвления при 3,6<= $\lambda$ <=3,9")
plt.xlabel("r")
plt.ylabel("$\lambda$ ")
plt.axvline(x=3.63,color='black',linestyle='--')
plt.axvline(x=3.74,color='black',linestyle='--')
plt.axvline(x=3.83,color='black',linestyle='--')
plt.axvline(x=3.9,color='black',linestyle='--')
plt.show()We
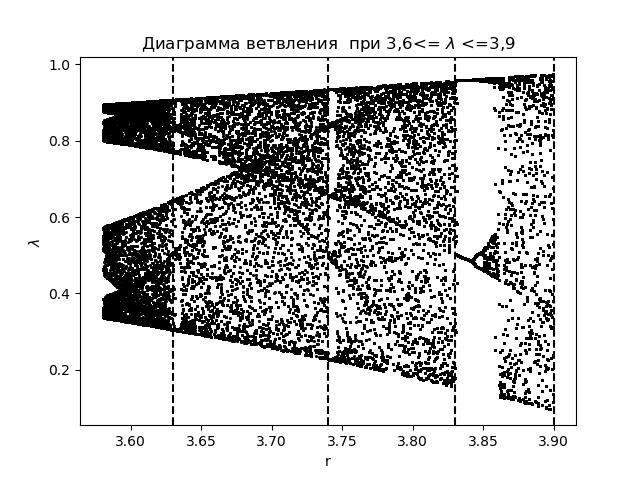
get : We plot for the entropy coefficient for the same areas
The graph for the entropy coefficient
import matplotlib.pyplot as plt
from numpy import*
data_k=[]
m='auto'
for p in arange(3.58,3.9,0.0001):
q=[round(p,2)]
M=zeros([1001,1])
for j in arange(0,1,1):
M[0,j]=0.5
for j in arange(0,1,1):
for i in arange(1,1001,1):
M[i,j]=q[j]*M[i-1,j]*(1-M[i-1,j])
a=[]
for i in arange(0,1001,1):
a.append(M[i,0])
n=len(a)
z=histogram(a, bins=m)
if type(m) is str:
m=len(z[0])
y=z[0]
d=z[1][1]-z[1][0]
h=0.5*d*n*10**(-sum([w*log10(w) for w in y if w!=0])/n)
ke=round(h/std(a),3)
data_k.append(ke)
plt.title("Энтропийный коэффициент ke для 3,6<= $\lambda$ <=3,9")
plt.plot(arange(3.58,3.9,0.0001),data_k)
plt.xlabel("$\lambda$ ")
plt.ylabel("ke")
plt.axvline(x=3.63,color='black',linestyle='--')
plt.axvline(x=3.74,color='black',linestyle='--')
plt.axvline(x=3.83,color='black',linestyle='--')
plt.axvline(x=3.9,color='black',linestyle='--')
plt.grid()
plt.show()We get:

Comparing the diagram and the graph, we see an identical display of the regions on the diagram and on the graph for the entropy coefficient for the function
For further analysis of the phenomena of information chaos using the entropy coefficient, we create a branch diagram for the logistic function:
Branch diagram
import matplotlib.pyplot as plt
from numpy import*
N=1000
y=[]
y.append(0.5)
for r in arange(2.25,2.56,0.0001):
for n in arange(1,N,1):
y.append(round(r*y[n-1]*(1-(y[n-1])**2),4))
y=y[N-250:N]
x=[r ]*250
plt.plot( x,y, color='black', linestyle=' ', marker='.', markersize=1)
plt.figure(1)
plt.title("Диаграмма ветвления при 2.25<=$\lambda$ <=2.56")
plt.xlabel("$\lambda$ ")
plt.ylabel("y")
plt.axvline(x=2.34,color='black',linestyle='--')
plt.axvline(x=2.39,color='black',linestyle='--')
plt.axvline(x=2.45,color='black',linestyle='--')
plt.axvline(x=2.49,color='black',linestyle='--')
plt.axvline(x=2.56,color='black',linestyle='--')
plt.show()
We
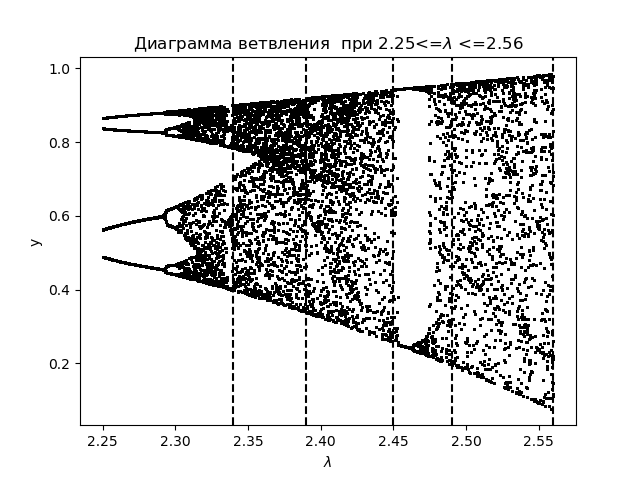
get : We plot for the entropy coefficient for the same areas
Entropy coefficient graph
import matplotlib.pyplot as plt
from numpy import*
data_k=[]
m='auto'
for p in arange(2.25,2.56,0.0001):
q=[round(p,2)]
M=zeros([1001,1])
for j in arange(0,1,1):
M[0,j]=0.5
for j in arange(0,1,1):
for i in arange(1,1001,1):
M[i,j]=q[j]*M[i-1,j]*(1-(M[i-1,j])**2)
a=[]
for i in arange(0,1001,1):
a.append(M[i,0])
n=len(a)
z=histogram(a, bins=m)
if type(m) is str:
m=len(z[0])
y=z[0]
d=z[1][1]-z[1][0]
h=0.5*d*n*10**(-sum([w*log10(w) for w in y if w!=0])/n)
ke=round(h/std(a),3)
data_k.append(ke)
plt.figure(2)
plt.title("Энтропийный коэффициент ke для 2.25<= $\lambda$ <=2.56")
plt.plot(arange(2.25,2.56,0.0001),data_k)
plt.xlabel("$\lambda$ ")
plt.ylabel("ke")
plt.axvline(x=2.34,color='black',linestyle='--')
plt.axvline(x=2.39,color='black',linestyle='--')
plt.axvline(x=2.45,color='black',linestyle='--')
plt.axvline(x=2.49,color='black',linestyle='--')
plt.axvline(x=2.56,color='black',linestyle='--')
plt.grid()
plt.show()
We get:
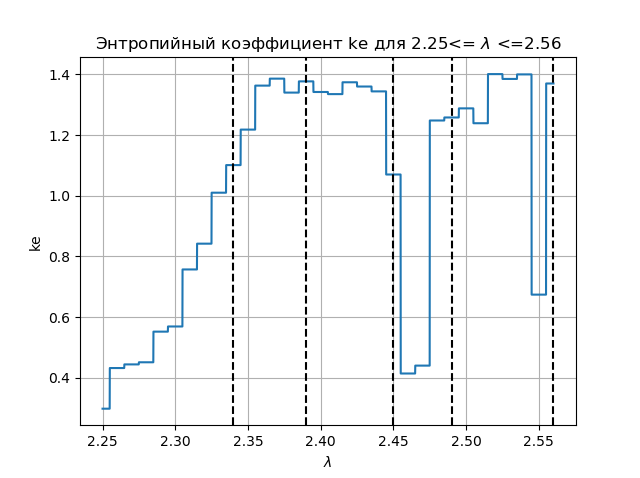
Comparing the diagram and the graph, we see an identical display of the regions on the diagram and on the graph for the entropy coefficient for the function
Conclusions:
The educational problem is solved in the article: is informational entropy a measure of chaos, and the answer of this question is affirmatively given by Python.
