A universal method for solving problems on the example of the puzzle "12 coins, 3 weighings"
Given: 12 coins, one of them is false, it differs only in weight. Unknown lighter or heavier. Leverage scales are given that show that the load on one side is heavier. For 3 weighings you need to find a fake coin.
From experience, I advise you not to rush, decide in writing. The puzzle “12 coins, 3 weighings” arose several times in my life. The first time my friend asked me, she decided after the Olympics and I had to break my head for a couple of hours. And a few years later it was not given to me right away. If you want to decide for yourself - do it on a piece of paper.
Below will be an analysis and stages of the solution. The stages will be carried out according to a universal methodology for solving problems, which is applicable both to programming and to life. With the approach, solving the puzzle will be easy.
I suggest you, before reading, offer a solution. Do you have an answer? Verified?
If it were software, the questions would be: “Have you programmed, tested the algorithm? Have you examined the test cases and checked them? ”
As experience shows, to solve it is necessary to draw a decision tree and check all 12 cases.

From experience, I advise you not to rush, decide in writing. The puzzle “12 coins, 3 weighings” arose several times in my life. The first time my friend asked me, she decided after the Olympics and I had to break my head for a couple of hours. And a few years later it was not given to me right away. If you want to decide for yourself - do it on a piece of paper.
Below will be an analysis and stages of the solution. The stages will be carried out according to a universal methodology for solving problems, which is applicable both to programming and to life. With the approach, solving the puzzle will be easy.
I suggest you, before reading, offer a solution. Do you have an answer? Verified?
If it were software, the questions would be: “Have you programmed, tested the algorithm? Have you examined the test cases and checked them? ”
As experience shows, to solve it is necessary to draw a decision tree and check all 12 cases.

1. Tips
In the process of solving it will help:
1) Decrease in entropy (measures of uncertainty) and answers to questions:
Вопросы подходят для любой задачи, проектов. Ответы на них помогают в снижении рисков срыва сроков, перерасхода бюджета и получения нагоняя от начальства.
2) Декомпозиция. Подход от простого к сложному. Если подготовить решение простейших случаев, затем использовать их для решения задачи (алгоритм разделяй и властвуй) то, будет проще, чем представлять всю ситуацию в голове.
Алгоритмы «разделяй и властвуй» разбивают задачу на две или более подзадачи того же типа, но меньшего размера до элементарных задач и объединяют их решения для получения ответа к исходной задаче.
Составьте вопросы для декомпозиции. Какие бы вы предложили?
1) Decrease in entropy (measures of uncertainty) and answers to questions:
- What did you learn in the previous step?
- What reduces uncertainty?
- What information do we have?
- What else do you need to know?
Вопросы подходят для любой задачи, проектов. Ответы на них помогают в снижении рисков срыва сроков, перерасхода бюджета и получения нагоняя от начальства.
2) Декомпозиция. Подход от простого к сложному. Если подготовить решение простейших случаев, затем использовать их для решения задачи (алгоритм разделяй и властвуй) то, будет проще, чем представлять всю ситуацию в голове.
Алгоритмы «разделяй и властвуй» разбивают задачу на две или более подзадачи того же типа, но меньшего размера до элементарных задач и объединяют их решения для получения ответа к исходной задаче.
Составьте вопросы для декомпозиции. Какие бы вы предложили?
2. Decomposition
Какие вопросы вы сформулировали для декомпозиции? Есть совпадения?
1) Какая ситуация самая элементарная? Что можем сделать за одно взвешивание?
За одно взвешивание можем определить, какая монета тяжелее, равен ли вес монет.
2) Если у нас 2 монеты, и, известно, фальшивая тяжелее или легче. Как за одно взвешивание определить фальшивую?
Необходимо взвесить монеты, и в зависимости от стрелки весов определить фальшивую.
3) Если у нас 2 монеты, и, не известно, фальшивая тяжелее или легче, как за одно взвешивание определить фальшивую?
Взвесив одну из 2-х представленных монет с третьей монетой, про которую известно, что она подлинная.
4) Если у нас 3 монеты, и, известно, фальшивая тяжелее или легче. Как за одно взвешивание определить фальшивую?
Необходимо сравнить любые две из этих монет, если они равны, фальшивой является третья монета.
5) Если у нас 3 монеты, и, неизвестно, фальшивая тяжелее или легче. Можно ли определить фальшивую за одно взвешивание?
К сожалению, нет.
6) Если у нас 4 монеты, и, неизвестно фальшивая тяжелее или легче, можно определить фальшивую за одно взвешивание?
К сожалению, нет.
7) Если у нас 4 монеты, и, неизвестно, фальшивая тяжелее или легче, за сколько взвешиваний можно определить фальшивую?
За два взвешивания.
Далее из элементарных случаев соберем ситуации из 8, 9, 10, 11 и 12 монет. Как вы видите решение?
Ниже полное решение.
1) Какая ситуация самая элементарная? Что можем сделать за одно взвешивание?
За одно взвешивание можем определить, какая монета тяжелее, равен ли вес монет.
2) Если у нас 2 монеты, и, известно, фальшивая тяжелее или легче. Как за одно взвешивание определить фальшивую?
Необходимо взвесить монеты, и в зависимости от стрелки весов определить фальшивую.
3) Если у нас 2 монеты, и, не известно, фальшивая тяжелее или легче, как за одно взвешивание определить фальшивую?
Взвесив одну из 2-х представленных монет с третьей монетой, про которую известно, что она подлинная.
4) Если у нас 3 монеты, и, известно, фальшивая тяжелее или легче. Как за одно взвешивание определить фальшивую?
Необходимо сравнить любые две из этих монет, если они равны, фальшивой является третья монета.
5) Если у нас 3 монеты, и, неизвестно, фальшивая тяжелее или легче. Можно ли определить фальшивую за одно взвешивание?
К сожалению, нет.
6) Если у нас 4 монеты, и, неизвестно фальшивая тяжелее или легче, можно определить фальшивую за одно взвешивание?
К сожалению, нет.
7) Если у нас 4 монеты, и, неизвестно, фальшивая тяжелее или легче, за сколько взвешиваний можно определить фальшивую?
За два взвешивания.
Далее из элементарных случаев соберем ситуации из 8, 9, 10, 11 и 12 монет. Как вы видите решение?
Ниже полное решение.
3. Decision
Первый шаг: разделим монеты на 3 группы по 4: 1 2 3 4, 5 6 7 8, 9 10 11 12.
Сравним первые две группы. Возможны три варианта:

1) Если группы равны, то фальшивая монета находится в третьей группе. Необходимо найти фальшивую монету из 4 монет за два взвешивания.
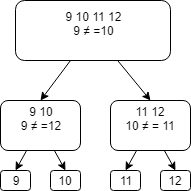
Делим третью группу на две: 9 10 11 12
Сравниваем 9 и 10:
Таким образом мы нашли фальшивую монету.
2) Рассмотрим второй случай. Если первая группа тяжелее второй, то присваиваем первой группе знак «>», второй группе знак «<», третьей группе – «0».

Делим монеты на группы 1 9 10 11 и 5 2 3 4, взвешиваем. Возможны три варианта:
3) Случай когда вторая группа тяжелее первой, аналогичен второму.
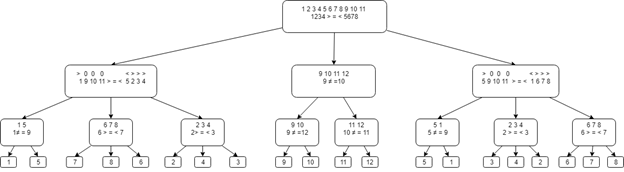
Общая диаграмма «Дерева решений» представлена ниже.
Сравним первые две группы. Возможны три варианта:
- первая группа тяжелее;
- вторая группа тяжелее;
- равны.

1) Если группы равны, то фальшивая монета находится в третьей группе. Необходимо найти фальшивую монету из 4 монет за два взвешивания.

Делим третью группу на две: 9 10 11 12
Сравниваем 9 и 10:
- если они равны, то фальшивая монета во второй группе – сравниваем 9 и 11. Если 9 и 11 равны — то фальшивая – 12, если нет -11
- если они не равны, то фальшивая в первой группе – сравниваем 10 и 12. Если 10 и 12 равны – фальшивая – 9, если нет – 10.
Таким образом мы нашли фальшивую монету.
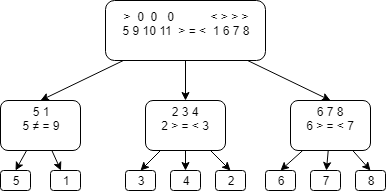
2) Рассмотрим второй случай. Если первая группа тяжелее второй, то присваиваем первой группе знак «>», второй группе знак «<», третьей группе – «0».

Делим монеты на группы 1 9 10 11 и 5 2 3 4, взвешиваем. Возможны три варианта:
- Равны. Фальшивая монета находится среди чисел: 6 7 8. Сравниваем 6 и 7, если равны – фальшивая — 8, если 6 больше, то фальшивая – 7, если 7 больше, то фальшивая – 6, так как в данном случае фальшивая монета легче.
- Первая группа тяжелее, то фальшивая монета либо 1, либо 5. Сравниваем 1 и 9, если они равны – фальшивая монета — 5, если нет — 1.
- Первая группа легче, то фальшивая среди монет 2 3 4, так как известно, что 9, 10 и 11 настоящие, и перевесить вторая группа может только за счет монет 2, 3 и 4. Сравниваем 2 и 3, если равны – фальшивая 4, если 2 тяжелее, то фальшивая – 2, иначе 3-я является фальшивой.
3) Случай когда вторая группа тяжелее первой, аналогичен второму.

Общая диаграмма «Дерева решений» представлена ниже.

Conclusion
При поступлении задачи на доработку или отладку хорошо применить рассмотренный выше подход:
Успешных решений.
- Определиться, что дано?
- На какие элементарные случаи\задачи можно разложить?
- Что неизвестно для решения задачи? Какие эксперименты нужно провести, чтобы снизить энтропию?
- Выполнить.
- Задача решена? Нет? Вернуться к шагу 1.
Успешных решений.
