How to speed up encryption according to GOST 28147-89 on the Baikal-T1 processor due to the SIMD block
- Tutorial
Using an example of a description of the encryption algorithm implementation in accordance with GOST 28147–89 built on the Feistel network, the article shows the capabilities of the BE-T1000 dual-core processor (aka Baikal-T1) and comparative tests of the algorithm implementation are carried out using vector calculations with and without SIMD coprocessor. Here we will demonstrate the use of the SIMD block for the encryption task in accordance with GOST 28147-89, ECB mode.
This article was written last year for the journal Electronic Components by Alexei Kolotnikov , a leading programmer at Baikal Electronics. And since there are not many readers in this magazine, and the article is useful for those who are professionally involved in cryptography, I, with the permission of the author and his small additions, publish it here.
The Baikal-T1 processor and the SIMD block inside it
The Baikal-T1 processor includes a multi-processor dual-core system of the MIPS32 P5600 family, as well as a set of high-speed interfaces for exchanging data and low-speed for controlling peripheral devices. Here is the structural diagram of this processor:
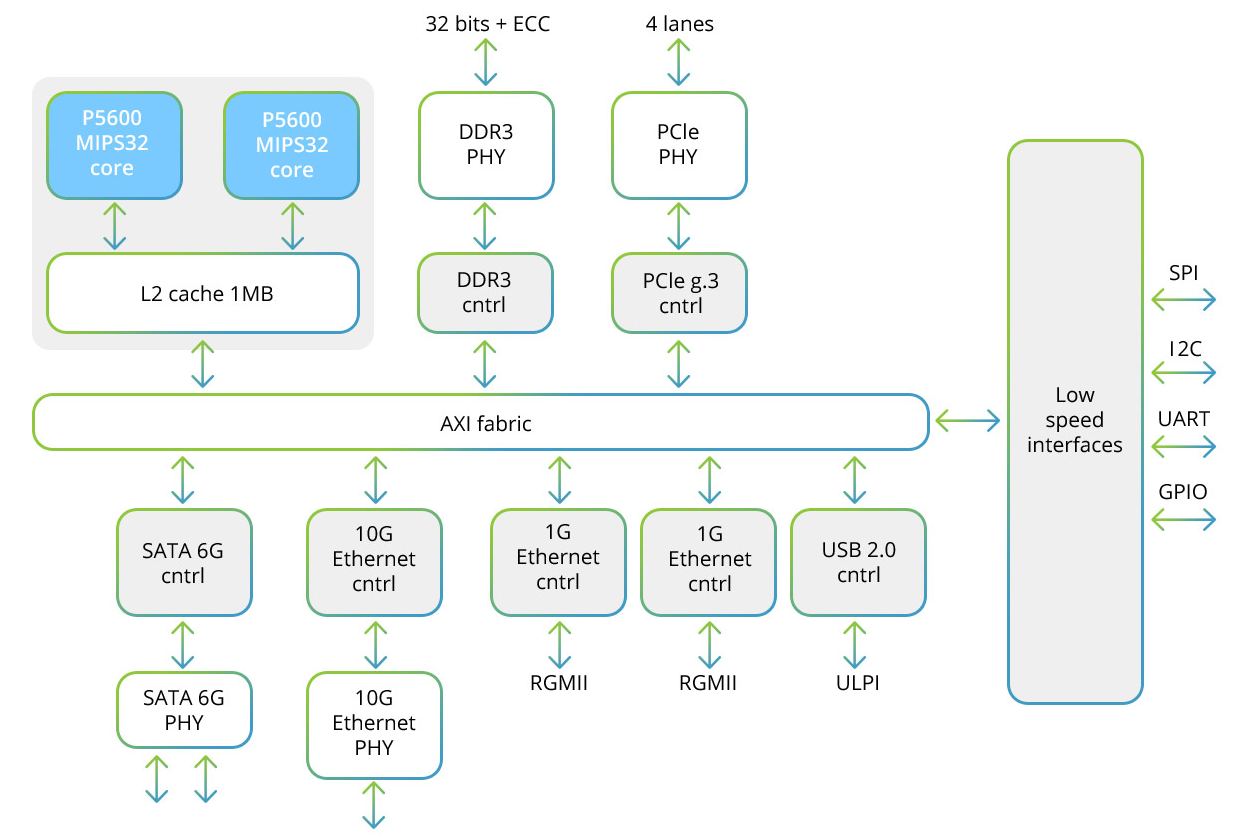
Each of the two cores includes a SIMD block that allows you to work with 128-bit vectors. When using the SIMD method, not one sample is processed,
but the entire vector, which can contain several samples, that is, one command is applied immediately to the entire vector (array) of data. Thus, in one command cycle, several samples are processed. The processor uses the MIPS32 SIMD block, which allows you to work with 32 pieces of 128-bit registers.
Each register can contain vectors of the following dimensions: 8 × 16; 16 × 8; 4 × 32 or
2 × 64 bits. It is possible to use more than 150 instructions for processing data: integer, floating-point and fixed-point, including bitwise operations, comparison operations, and conversion operations.
Very detailed MIPS SIMD technology was described by SparF in the article "MIPS SIMD Technology and the Baikal-T1 Processor" .
Evaluation of the effectiveness of vector computing
The arithmetic coprocessor of the Baikal-T1 processor core combines a traditional floating-point processor and a parallel SIMD processor, focused on the efficient processing of vectors and digitized signals. An independent performance assessment of the vector SIMD coprocessor was carried out in 2017 by SparF while writing the article “MIPS SIMD Technology and the Baikal-T1 Processor” . If desired, such measurements can be repeated, performed independently by connecting to a remote stand with a processor .
Then the test task was to decode the video encoded using the free x264 libraries (H.264 demo clip) and x265 (HEVC video file), with screenshots taken at regular intervals. As expected, a noticeable increase in the processor core performance on FFmpeg tasks with the use of SIMD hardware capabilities was noted:

Brief description of the algorithm GOST 28147-89
Here we will only note the main characteristics for understanding the code and optimization:
- The algorithm is built on the Feistel network.

- The algorithm consists of 32 rounds.
- A round consists of mixing a key and replacing 8 parts of 4 bits in a table with a shift of 11 bits.
A detailed description of the information conversion algorithm in accordance with GOST 28147-89 is given in the State Standard of the USSR .
Implementation of the GOST 28147-89 algorithm without using a SIMD block
For comparison purposes, the algorithms were initially implemented using standard, “non-vectorized” commands.
The MIPS assembler code proposed here allows you to encrypt one block of 64 bits in 450 ns (or ~ 150 Mb / s) at a nominal processor frequency of 1200 MHz. Only one core is involved in the calculations.
Preparing a replacement table implies expanding it into a 32-bit representation to speed up the work of the round: instead of replacing four bits with masking and shifting, a previously
prepared table performs eight-bit replacement.
uint8_t sbox_test[8][16] = {
{0x9, 0x6, 0x3, 0x2, 0x8, 0xb, 0x1, 0x7, 0xa, 0x4, 0xe, 0xf, 0xc, 0x0, 0xd, 0x5},
{0x3, 0x7, 0xe, 0x9, 0x8, 0xa, 0xf, 0x0, 0x5, 0x2, 0x6, 0xc, 0xb, 0x4, 0xd, 0x1},
{0xe, 0x4, 0x6, 0x2, 0xb, 0x3, 0xd, 0x8, 0xc, 0xf, 0x5, 0xa, 0x0, 0x7, 0x1, 0x9},
{0xe, 0x7, 0xa, 0xc, 0xd, 0x1, 0x3, 0x9, 0x0, 0x2, 0xb, 0x4, 0xf, 0x8, 0x5, 0x6},
{0xb, 0x5, 0x1, 0x9, 0x8, 0xd, 0xf, 0x0, 0xe, 0x4, 0x2, 0x3, 0xc, 0x7, 0xa, 0x6},
{0x3, 0xa, 0xd, 0xc, 0x1, 0x2, 0x0, 0xb, 0x7, 0x5, 0x9, 0x4, 0x8, 0xf, 0xe, 0x6},
{0x1, 0xd, 0x2, 0x9, 0x7, 0xa, 0x6, 0x0, 0x8, 0xc, 0x4, 0x5, 0xf, 0x3, 0xb, 0xe},
{0xb, 0xa, 0xf, 0x5, 0x0, 0xc, 0xe, 0x8, 0x6, 0x2, 0x3, 0x9, 0x1, 0x7, 0xd, 0x4}
};
uint32_t sbox_cvt[4*256];
for (i = 0; i < 256; ++i) {
uint32_t p;
p = sbox[7][i >> 4] << 4 | sbox[6][i & 15];
p = p << 24; p = p << 11 | p >> 21;
sbox_cvt[i] = p; // S87
p = sbox[5][i >> 4] << 4 | sbox[4][i & 15];
p = p << 16; p = p << 11 | p >> 21;
sbox_cvt[256 + i] = p; // S65
p = sbox[3][i >> 4] << 4 | sbox[2][i & 15];
p = p << 8; p = p << 11 | p >> 21;
sbox_cvt[256 * 2 + i] = p; // S43
p = sbox[1][i >> 4] << 4 | sbox[0][i & 15];
p = p << 11 | p >> 21;
sbox_cvt[256 * 3 + i] = p; // S21
}Block encryption is 32 times a repeat of the round using the key.
// input: a0 - &in, a1 - &out, a2 - &key, a3 - &sbox_cvt
LEAF(gost_encrypt_block_asm)
.set reorder
lw n1, (a0) // n1, IN
lw n2, 4(a0) // n2, IN + 4
lw t0, (a2) // key[0] -> t0
gostround n1, n2, 1
gostround n2, n1, 2
gostround n1, n2, 3
gostround n2, n1, 4
gostround n1, n2, 5
gostround n2, n1, 6
gostround n1, n2, 7
gostround n2, n1, 0
gostround n1, n2, 1
gostround n2, n1, 2
gostround n1, n2, 3
gostround n2, n1, 4
gostround n1, n2, 5
gostround n2, n1, 6
gostround n1, n2, 7
gostround n2, n1, 0
gostround n1, n2, 1
gostround n2, n1, 2
gostround n1, n2, 3
gostround n2, n1, 4
gostround n1, n2, 5
gostround n2, n1, 6
gostround n1, n2, 7
gostround n2, n1, 7
gostround n1, n2, 6
gostround n2, n1, 5
gostround n1, n2, 4
gostround n2, n1, 3
gostround n1, n2, 2
gostround n2, n1, 1
gostround n1, n2, 0
gostround n2, n1, 0
1: sw n2, (a1)
sw n1, 4(a1)
jr ra
nop
END(gost_encrypt_block_asm)A spread table round is just a table swap.
.macro gostround x_in, x_out, rkey
addu t8, t0, \x_in /* key[0] + n1 = x */
lw t0, \rkey * 4 (a2) /* next key to t0 */
ext t2, t8, 24, 8 /* get bits [24,31] */
ext t3, t8, 16, 8 /* get bits [16,23] */
ext t4, t8, 8, 8 /* get bits [8,15] */
ext t5, t8, 0, 8 /* get bits [0, 7] */
sll t2, t2, 2 /* convert to dw offset */
sll t3, t3, 2 /* convert to dw offset */
sll t4, t4, 2 /* convert to dw offset */
sll t5, t5, 2 /* convert to dw offset */
addu t2, t2, a3 /* add sbox_cvt */
addu t3, t3, a3 /* add sbox_cvt */
addu t4, t4, a3 /* add sbox_cvt */
addu t5, t5, a3 /* add sbox_cvt */
lw t6, (t2) /* sbox[x[3]] -> t2 */
lw t7, 256*4(t3) /* sbox[256 + x[2]] -> t3 */
lw t9, 256*2*4(t4) /* sbox[256 *2 + x[1]] -> t4 */
lw t1, 256*3*4(t5) /* sbox[256 *3 + x[0]] -> t5 */
or t2, t7, t6 /* | */
or t3, t1, t9 /* | */
or t2, t2, t3 /* | */
xor \x_out, \x_out, t2 /* n2 ^= f(...) */
.endmThe implementation of the algorithm of GOST 28147-89 with the use of SIMD-unit
The code proposed below allows you to simultaneously encrypt four blocks of 64 bits per 720 ns (or ~ 350 Mbit / s) under the same conditions: processor frequency 1200 MHz, one core.
Replacement is carried out in two quadruples and immediately in 4 blocks with instructions shuffleand subsequent masking of significant fours.
Expanding a substitution table
for(i = 0; i < 16; ++i) {
sbox_cvt_simd[i] = (sbox[7][i] << 4) | sbox[0][i]; // $w8 [7 0]
sbox_cvt_simd[16 + i] = (sbox[1][i] << 4) | sbox[6][i]; // $w9 [6 1]
sbox_cvt_simd[32 + i] = (sbox[5][i] << 4) | sbox[2][i]; // $w10[5 2]
sbox_cvt_simd[48 + i] = (sbox[3][i] << 4) | sbox[4][i]; // $w11[3 4]
}Initializing masks.
l0123: .int 0x0f0f0f0f
.int 0xf000000f /* substitute from $w8 [7 0] mask in w12*/
.int 0x0f0000f0 /* substitute from $w9 [6 1] mask in w13*/
.int 0x00f00f00 /* substitute from $w10 [5 2] mask in w14*/
.int 0x000ff000 /* substitute from $w11 [4 3] mask in w15*/
.int 0x000f000f /* mask $w16 x N x N */
.int 0x0f000f00 /* mask $w17 N x N x */
LEAF(gost_prepare_asm)
.set reorder
.set msa
la t1, l0123 /* masks */
lw t2, (t1)
lw t3, 4(t1)
lw t4, 8(t1)
lw t5, 12(t1)
lw t6, 16(t1)
lw t7, 20(t1)
lw t8, 24(t1)
fill.w $w2, t2 /* 0f0f0f0f -> w2 */
fill.w $w12, t3 /* f000000f -> w12*/
fill.w $w13, t4 /* 0f0000f0 -> w13*/
fill.w $w14, t5 /* 00f00f00 -> w14*/
fill.w $w15, t6 /* 000ff000 -> w15*/
fill.w $w16, t7 /* 000f000f -> w16*/
fill.w $w17, t8 /* 0f000f00 -> w17*/
ld.b $w8, (a0) /* load sbox */
ld.b $w9, 16(a0)
ld.b $w10, 32(a0)
ld.b $w11, 48(a0)
jr ra
nop
END(gost_prepare_asm)4 block encryption
LEAF(gost_encrypt_4block_asm)
.set reorder
.set msa
lw t1, (a0) // n1, IN
lw t2, 4(a0) // n2, IN + 4
lw t3, 8(a0) // n1, IN + 8
lw t4, 12(a0) // n2, IN + 12
lw t5, 16(a0) // n1, IN + 16
lw t6, 20(a0) // n2, IN + 20
lw t7, 24(a0) // n1, IN + 24
lw t8, 28(a0) // n2, IN + 28
lw t0, (a2) // key[0] -> t0
insert.w ns1[0],t1
insert.w ns2[0],t2
insert.w ns1[1],t3
insert.w ns2[1],t4
insert.w ns1[2],t5
insert.w ns2[2],t6
insert.w ns1[3],t7
insert.w ns2[3],t8
gostround4 ns1, ns2, 1
gostround4 ns2, ns1, 2
gostround4 ns1, ns2, 3
gostround4 ns2, ns1, 4
gostround4 ns1, ns2, 5
gostround4 ns2, ns1, 6
gostround4 ns1, ns2, 7
gostround4 ns2, ns1, 0
gostround4 ns1, ns2, 1
gostround4 ns2, ns1, 2
gostround4 ns1, ns2, 3
gostround4 ns2, ns1, 4
gostround4 ns1, ns2, 5
gostround4 ns2, ns1, 6
gostround4 ns1, ns2, 7
gostround4 ns2, ns1, 0
gostround4 ns1, ns2, 1
gostround4 ns2, ns1, 2
gostround4 ns1, ns2, 3
gostround4 ns2, ns1, 4
gostround4 ns1, ns2, 5
gostround4 ns2, ns1, 6
gostround4 ns1, ns2, 7
gostround4 ns2, ns1, 7
gostround4 ns1, ns2, 6
gostround4 ns2, ns1, 5
gostround4 ns1, ns2, 4
gostround4 ns2, ns1, 3
gostround4 ns1, ns2, 2
gostround4 ns2, ns1, 1
gostround4 ns1, ns2, 0
gostround4 ns2, ns1, 0
1:
copy_s.w t1,ns2[0]
copy_s.w t2,ns1[0]
copy_s.w t3,ns2[1]
copy_s.w t4,ns1[1]
copy_s.w t5,ns2[2]
copy_s.w t6,ns1[2]
copy_s.w t7,ns2[3]
copy_s.w t8,ns1[3]
sw t1, (a1) // n2, OUT
sw t2, 4(a1) // n1, OUT + 4
sw t3, 8(a1) // n2, OUT + 8
sw t4, 12(a1) // n1, OUT + 12
sw t5, 16(a1) // n2, OUT + 16
sw t6, 20(a1) // n1, OUT + 20
sw t7, 24(a1) // n2, OUT + 24
sw t8, 28(a1) // n1, OUT + 28
jr ra
nop
END(gost_encrypt_4block_asm) Round using SIMD block commands with calculation of 4 blocks simultaneously
.macro gostround4 x_in, x_out, rkey
fill.w $w0, t0 /* key -> Vi */
addv.w $w1, $w0, \x_in /* key[0] + n1 = x */
srli.b $w3, $w1, 4 /* $w1 >> 4 */
and.v $w4, $w1, $w16 /* x 4 x 0*/
and.v $w5, $w1, $w17 /* 6 x 2 x*/
and.v $w6, $w3, $w17 /* 7 x 3 x */
and.v $w7, $w3, $w16 /* x 5 x 1 */
lw t0, \rkey * 4(a2) /* next key -> t0 */
or.v $w4, $w6, $w4 /* 7 4 3 0 */
or.v $w5, $w5, $w7 /* 6 5 2 1 */
move.v $w6, $w5 /* 6 5 2 1 */
move.v $w7, $w4 /* 7 4 3 0 */
/* 7 x x 0 */
/* 6 x x 1 */
/* x 5 2 x */
/* x 4 3 x */
vshf.b $w4, $w8, $w8 /* substitute $w8 [7 0] */
and.v $w4, $w4, $w12
vshf.b $w5, $w9, $w9 /* substitute $w9 [6 1] */
and.v $w5, $w5, $w13
vshf.b $w6, $w10, $w10 /* substitute $w10 [5 2] */
and.v $w6, $w6, $w14
vshf.b $w7, $w11, $w11 /* substitute $w11 [4 3] */
and.v $w7, $w7, $w15
or.v $w4, $w4, $w5
or.v $w6, $w6, $w7
or.v $w4, $w4, $w6
srli.w $w1, $w4, 21 /* $w4 >> 21 */
slli.w $w3, $w4, 11 /* $w4 << 11 */
or.v $w1, $w1, $w3
xor.v \x_out, \x_out, $w1
.endmBrief conclusions
Using the SIMD-block of the Baikal-T1 processor allows achieving a data conversion rate of about 350 Mbit / s according to GOST 28147-89 algorithms, which is two and a half (!) Times higher than the implementation on standard commands. Since this processor has two cores, it is theoretically possible to encrypt a stream at a speed of ~ 700 Mbit / s. At least the test implementation of IPsec, with encryption according to GOST 28147-89, showed the channel throughput of ~ 400 Mbps on a duplex.
