Unusually interconnecting qubits, D-Wave significantly increased the speed of a quantum computer

“The Great Wave in Kanagawa” - a woodcut by 19th-century Japanese artist Katsushiki Hokusai

In early March, D-Wave Systems announced the release of their new computer operating on the principle of quantum annealing . The new machine made several technical improvements, as well as significantly changed the physical location of the components. What does this mean? Along with D-Wave’s online resources, a device approaching a state of usefulness is beginning to take shape.

Making a smooth computer

Before you get to the delicious filling, you first need to gnaw at the edge of the cookie - that is, find out what is quantum annealing? Most computers work in a straightforward way: to add two numbers, we create a set of logic gates that will perform the addition. Each of the gates performs a set of its clearly defined operations on the input data.

But this is not the only way to do the calculations. Most of the tasks can be written so that they are equivalent to the task of minimizing energy. In this version, the task is an energy landscape, and the solution is the minimum possible energy on it. The bottom line is to find a combination of bit values ​​denoting this energy.

To do this, you need to start with a flat energy landscape: all bits will have minimal energy. Then we slowly and carefully change the landscape around the bits until it begins to represent our task. If everything is done correctly, then the bits will remain in a state with minimal energy. We get the solution by considering their values.

Although all this works without quantum physics, D-Wave does this with the help of quantum bits (qubits). This means that qubits correlate with each other - this is called quantum entanglement. As a result, they change their values ​​together, and not separately.

Tunneling

As a result, an effect known as quantum tunneling becomes possible. Imagine a qubit stuck in a state of high energy. Nearby there is a state with less energy into which the qubit would like to go. But to get there, he first needs to go into a state with more energy. In the classical system, this turns into a barrier to achieving a state with less energy. But in a quantum qubit, it can tunnel through an energy barrier, entering a state with less energy.

These two properties can allow a computer that is controlled by D-Wave to find solutions to some problems faster than a classic.

But the devil is hiding in the little things. In a computer, the energy landscape is built by the binding (physical union) of qubits. Linking controls how much the value of one qubit affects the value of the rest.

This moment has always been a problem for the machine from D-Wave. Under ideal conditions, each qubit will have connections with every other qubit. But organizing such a large number of connections is impractical.

Cubits on its own

The consequences of the lack of connections are very serious. Some tasks simply cannot be redone to solve on D-Wave machines. And sometimes, in cases where the task can be redone, the calculations will be ineffective. Imagine that to solve the problem, you need to connect qubits with numbers one and three, but they are not directly connected. In this case, you have to look for qubits common to both of them. Suppose qubit one is connected to qubit five, and qubit two is connected to qubits five and three. Then the logical qubit one will be a combination of the first and fifth. Logical qubit three - a combination of the second and third. D-Wave calls this sequence the length of the chain. In this case, the length is two.

Due to the connection into chains of physical qubits to obtain logical qubits, fewer qubits remain available for calculation.

D-Wave planned to build even more complex qubit patterns to increase connectivity. The greater the connectivity, the shorter the length of the chains, the more free logical qubits. And if qubits are tightly connected together, and the connectivity is large, then with the help of such a machine more problems can be solved.

The efficiency of structuring some tasks will be extremely low, that is, the D-Wave architecture is simply not suitable for their solution. But with increasing connectivity, the number of inappropriate tasks will decrease.

In the previous version of the machine, qubits were distributed in blocks of eight pieces in order to improve the connectivity of the diagonal blocks compared to the previous version of the machine. As a result, the situation with chain lengths has improved somewhat.


D-Wave 2000Q Architecture

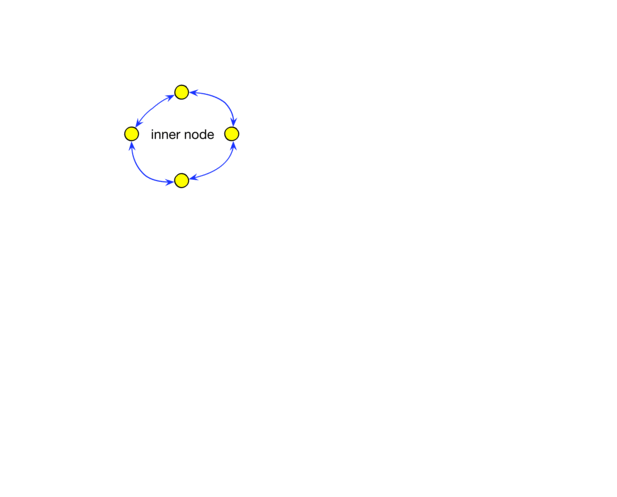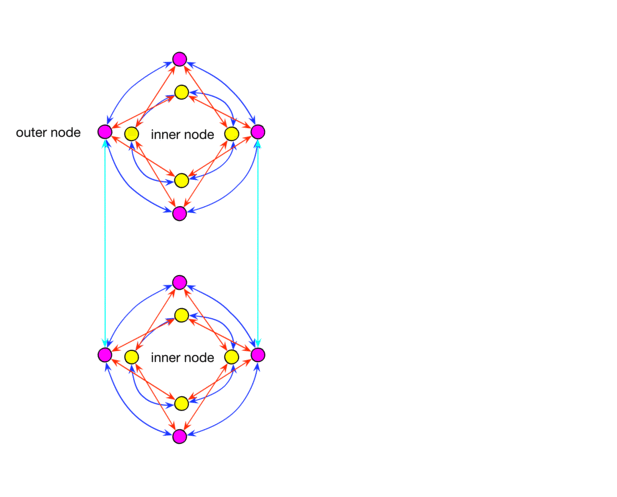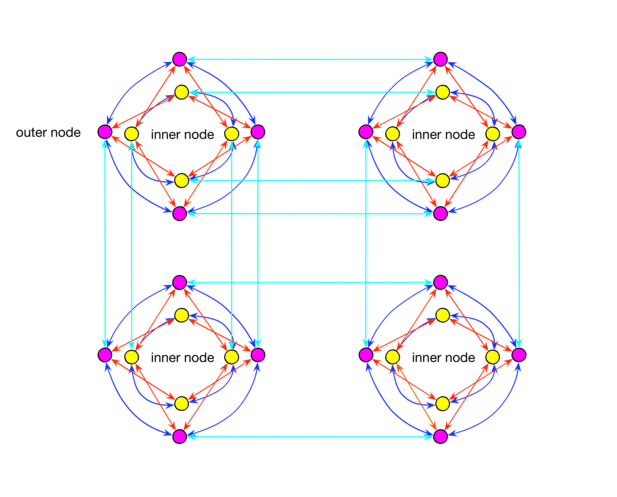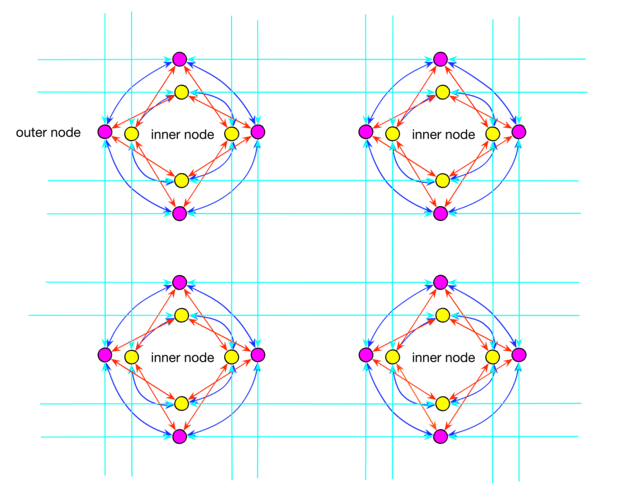
Now D-Wave has switched to a connectivity scheme known as the “Count of Pegasus." I don’t know how to describe it exactly, so I’ll describe it not very correctly from the point of view of a rigorous graph theory, but it’s more clear. Instead of identical blocks of eight qubits, the machine now has two types of blocks: eight pieces and two pieces.

In blocks of eight qubits, as before, are located along the inner and outer loops. But, as shown in the video, now the internal and external loops have additional connections. This means that each qubit in a small block has five links.

The blocks themselves are no longer arranged in the correct lattice, and there are more connections between qubits from different blocks. In the previous generation, qubits on external loops were connected with other qubits on external loops, and now each qubit is connected with both internal and external loops of neighboring blocks.



In addition, a new network of long-distance communications between different blocks has appeared. Each qubit has a relatively distant connection with another qubit in the remote unit. The density of the distant joints increases due to the second main building block, consisting of a combined pair of qubits. Pairs are located around the main blocks and complement the distant connectivity.

The idea is that in groups of eight qubits located on the edge of the chip, the bond density is almost the same as that of the internal groups, unlike graphs of the “chimera” class.

Chain shortening

What does all this mean? Firstly, the similarity of the “chimera” and “pegasus” columns means that the code developed for the “chimera” should work on the pegasus as well. Increased connectivity means reduced chain lengths and increased reliability.

So that you can imagine how much the new graph improves the situation, I will say that a square lattice with diagonal connections requires chains of six units in graphs of the “chimera” type and two units in graphs of the “Pegasus” type. In general, the length of the chains is reduced by two or more times. As a result, the operating time is reduced by 30-75%.

In addition to the new graph, D-Wave improved the computer's work at a technical level: the noise level of qubits is less, and their number has increased significantly. The company plans using the new architecture to bring the number of qubits to 5000 (since 2000). All these architectural changes mean that much more physical qubits can be used as independent logical ones, so the upgrade will be much more significant.