“2048” in a few weeks turns 5 years old, which means it's time to write something dedicated to this wonderful game.

Particularly informative is the topic of independent game of artificial intelligence in a puzzle. Ways of implementation are the most different and today we will analyze the relatively easy ones. Namely, we will teach the computer mind to collect the degrees of two using the Monte Carlo method.

The article was written with the support of the company EDISON Software, which develops mobile applications and provides software testing services .

The inspiration for this work was the discussion on stackoverflow, where smart guys offered effective ways of playing computer games . Apparently, the best way is the minimax method with alpha-beta clipping and in a couple of days the next publication will be devoted to it.

The casino method is suggested by the stackoverflow Ronenz user as part of the above discussion. The whole next section is a translation from its publication.

Monte Carlo method

I became interested in the idea of ​​AI for this game, in which there is no hard-coded intelligence (that is, there are no heuristics, scoring, etc.). The AI ​​must “know” only the rules of the game and “understand” the game. This distinguishes it from most AIs (such as in this topic), since the gameplay is in fact a brute force driven by a scoring function that reflects the human understanding of the game.

AI algorithm

I found a simple, but surprisingly good game algorithm: to determine the next move for a given field condition, the AI ​​plays the game in RAM, making random moves until the game ends in defeat. This is done several times, while the final score is tracked. Then the average final score is calculated taking into account the initial move. The initial move that showed the highest average result is selected as the actually selected move.

With 100 runs for each initial move, the AI ​​gets to tile 2048 in 80% of cases and tile 4096 in 50% of cases. When using 10,000 runs, 2048 is obtained in 100% of cases, 70% for 4096 and about 1% for 8192.

See in action The

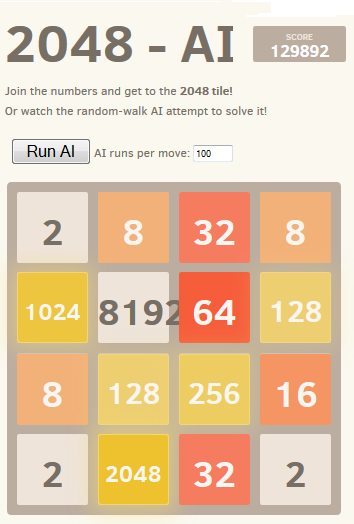
best result achieved is shown in the screenshot:

An interesting fact for this algorithm is that although games with randomly performed moves are expectedly rather bad, nevertheless, the choice of the best (or least bad, if you like) move leads to a very good gameplay: a typical Monte Carlo AI game can score 70,000 points for 3000 moves, however games with a random game in memory from any given position give an average of 340 additional points for about 40 additional moves before a loss. (You can verify this yourself by running the AI ​​and opening the debugging console.)

This graph illustrates this concept: the blue line shows the score of the game after each turn. The red line shows the bestthe result of the algorithm, arbitrarily making moves from this position to the end of the game. In fact, the red values ​​“pull up” the blue ones, since they are the best offers of the algorithm. Interestingly, the red line is just a little above the blue line at each point, but the blue line narrows the gap more and more.


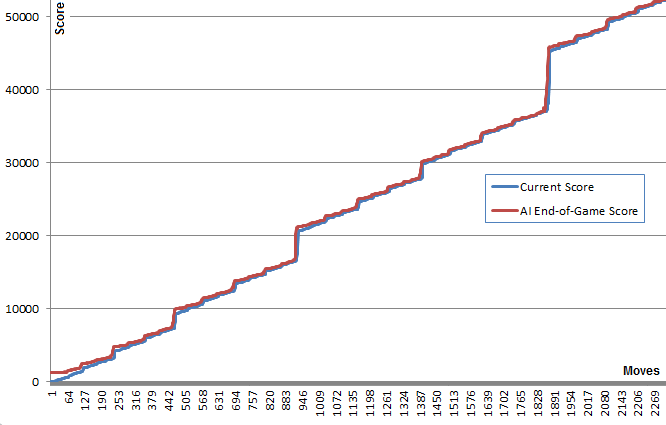
I find it rather surprising that the algorithm actually does not necessarily foresee a good gameplay, and nevertheless selects the moves that it (the good process) produces.

Later, I discovered that this method can be classified as a Monte Carlo search algorithm .

Implementation and links

First, I created a JavaScript version that can be seen in action here . This version is able to run 100 runs in a reasonable time. Open the console for more information. ( source )

Later, to play around, I used the highly optimized @nneonneo infrastructure and implemented my version in C ++. This version allows up to 100,000 runs per turn and even 1,000,000 if you are ready to wait. Assembly instructions are attached. Everything works in the console, and also has a remote control for playback in the web version. ( source )

results

Surprisingly, an increase in the number of runs does not drastically improve the gameplay. It seems that this strategy has a limit of 80,000 points with 4096 tiles and all the lesser results very close to achieving tile 8192. Increasing the number of runs from 100 to 100,000 increases the chances of reaching this limit (from 5% to 40%), but not overcomes it.

Performing 10,000 runs with a temporary increase of up to 1,000,000 near critical positions made it possible to overcome this barrier in less than 1% of cases with the achievement of the maximum number of points scored 129892 and tile 8192.

Improvements and optimizations

After implementing this algorithm, I tried many improvements, including the use of minimum or maximum estimates, or a combination of minimum, maximum and average values. I also tried to use depth: instead of trying to perform K runs per turn, I tried K moves for a list of moves of a given length (for example, “up, up, left”) and selected the first move from the list of moves with the best win.

Later, I implemented a scoring tree, which took into account the conditional probability that he would be able to complete a move after a given list of moves.

However, none of these ideas showed a real advantage over the simple first idea. I left the commented out code for these ideas in the C ++ source code.

I added the Deep Search mechanism, which temporarily increased the number of runs to 1,000,000, when any of the runs accidentally managed to reach the next highest tile. This led to an improvement with respect to time s performance tests.

I would be interested to know if anyone has any other improvement ideas that support the independence of AI from the subject area?

Variants and clones 2048

For the sake of interest, I also implemented the AI ​​in the form of a bookmarklet, connecting it to the game controls. This allows you to work with the original game, and with many of its variations.

This is possible due to the domain-independent nature of AI. Some of the options are quite original, such as a hexagonal clone.

This translation is complete, but not only for the sake of this publication started this publication. Before the colic, I wanted to test various ideas for AI in 2048 myself. For this purpose, I implemented the game in Excel by writing an application with macros. The implementation on VBA itself is not a feat - it’s googling, you can quickly find out with a dozen different ecclesiastical handicrafts. But not only to concoct 2048 in the form of spreadsheets, but also to realize a computer independent game - this has not come across to me so far.

2048.xlsm

The Excel application itself can be downloaded from the Google disk .

The picture is clickable - a full-size image will open. Briefly on the interface and application functionality. To start playing, you need to click on the button " User: start the game ." When you press this button again, the inscription changes from " User: start the game " to " User: complete the game " and back, that is, at any time you can stop the game and then start it again. When you stop the game, you can manually change the alignment on the field, improving or worsening your position in order to test or test some ideas. During the game itself, you can make moves in two ways:

• Keyboard: simply by pressing the up, down, left, right keys.
• Using the mouse: clicking on the cells with large arrows pointing to the right direction.

The " New Field " button clears the playing field and randomly places "two" and "four" on it.

The most interesting thing is that the Monte Carlo method was implemented, precisely in the form in which the guy suggested it with stackoverflow. At each position, the computer in memory goes through random branches for each first move (“up”, “down”, “left”, “right”) until it results in a loss. The statistically most favorable direction is highlighted in red in a special table below. You can use it as a hint if you see that your own game comes to a standstill and you need to somehow save yourself. ;)

Above the table are checkboxes with analysis options. At the moment, only Monte-Carlo is solved, the rest will be added in the coming days (according to the results of which there will be more habrastation with updating the excel application and explanations on the theory).

There is also an " AI: game " button . Clicking on it, the computer assistant will make one move in accordance with the Monte Carlo method or some other method selected in the switch group (the minimax and neural network will work in this list a little later).