The task of N bodies or how to blow up a galaxy without leaving the kitchen
Not so long ago I read the science fiction novel “The Three-Body Problem” by Liu Qixin . In it, some aliens had a problem - they did not know how, with sufficient accuracy for them, to calculate the trajectory of their home planet. Unlike us, they lived in a three-star system, and the “weather” on the planet depended strongly on their mutual arrangement - from the incinerating heat to the icy cold. And I decided to check whether we can solve such problems.
Physics of the phenomenon
To understand the problem, it is necessary to deal with the physics of the phenomenon. In the framework of the classical theory, the attractive force of two bodies is determined by Newton's law :
Where
In the system of
Using Newton’s second law, we write the acceleration for each particle:
Recalling that acceleration is the second time derivative of the coordinate, we obtain a second-order partial differential equation, which must be solved to obtain the trajectory of each body:
It is important to note here that the complexity of computing a function
Maths
The first and simplest method for solving differential equations is the Euler method , which is designed to solve equations of the form:
Upon transition to the discrete region, we obtain:
Where
To apply the Euler method to our problem, it should be reduced to a first-order system. To do this, we introduce an additional variable - particle velocity:
The second problem in solving systems of differential equations is the accuracy of the solution and its control. Accuracy can be improved in two ways: by decreasing the integration step and choosing a method with a higher order of accuracy. Both methods lead to increased computational complexity, but in different ways. For example, you can use the classical fourth-order Runge-Kutta method ; it requires four function calculations
Also, each of these methods has its drawbacks. Analytical decisions may be absent, or, even in most cases, completely absent. For example, for our task
Note on calculating total energy
In our case, the total energy of the system consists of two parts - kinetic and potential energy. Kinetic energy consists of the sum of the kinetic energies of all bodies. To calculate the potential energy, we need to add the potential energies of each particle in the gravitational field of the remaining particles, so we need to add terms. The difficulty is that all terms are of a very different order, and even with double-precision calculations it is not possible to calculate this value with an accuracy sufficient for comparison at different steps. To overcome this problem, it was necessary to apply summation according to the Kahan algorithm .
terms. The difficulty is that all terms are of a very different order, and even with double-precision calculations it is not possible to calculate this value with an accuracy sufficient for comparison at different steps. To overcome this problem, it was necessary to apply summation according to the Kahan algorithm .
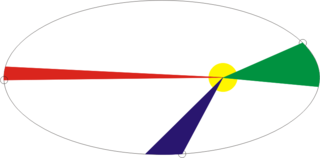
Fig 1. An example of an elliptical trajectory.
Consider the simple case of a satellite moving in an elliptical orbit around the Earth. As the satellite approaches the Earth, its speed increases, and when moving away from the Earth it decreases, accordingly, the possibility arises of decreasing the integration step in time in the green part of the orbit, and increasing it in red and blue without changing the accuracy of the solution. Let's try to compare in more detail.
Table 1. Investigated methods for solving differential equations
| Marked | Order | Description |
|---|---|---|
| adams | 1-5 | Adams-Bashfort Method |
| euler | 1 | Euler Method |
| rk4 | 4 | Classic Runge-Kutta Method |
| rkck | 5 | Kash-Karp Method |
| rkdp | 5 | Dorman-Prince Method |
| rkdverk | 6 | Werner Method 1) p. 181 |
| rkf | 7 | Felberg Method 1) p. 180 |
| rkgl | 6 | Implicit Gauss-Legendre Method |
| rklc | 4 | Implicit Lobatto Method |
| trapeze | 2 | Trapezoid method |
To select the best method for our task, we will compare several known methods. To do this, we simulate the collision of two systems of bodies
| a) | b) |
| Figure 2. Relative change in energy a), momentum b), at the end of system simulation | |
From the graphs of Figure 2 it can be seen that the best ratio of the amount of function calculation
| a) | b) |
| Fig. 3. Relative change in energy a), momentum b), at the end of system simulation | |
Figures 3a and 3b show that the use of calculations with quadruple accuracy can reduce the relative energy losses up to
The Dorman-Prince and Werner methods belong to the class of nested methods and can simultaneously calculate two solutions with a high and low order of accuracy (for the Dorman-Prince method, orders 5 and 4, and for the Werner method, orders 6 and 5). If these two solutions are very different, then we can break the current integration step into smaller ones. That allows us to dynamically change the integration step and reduce it only in those areas where it is required.
Let us compare the fifth-order Dorman-Prince, Werner, and Adams methods in more detail, over a longer simulation interval of our system (
| Fig. 6. Relative change in energy, momentum and its moment in the process of modeling by the fifth-order Adams-Bashfort method with a step |
| Fig 7. Dependences of the number of function calculations |
It can be seen that at the initial stage of the evolution of our system (
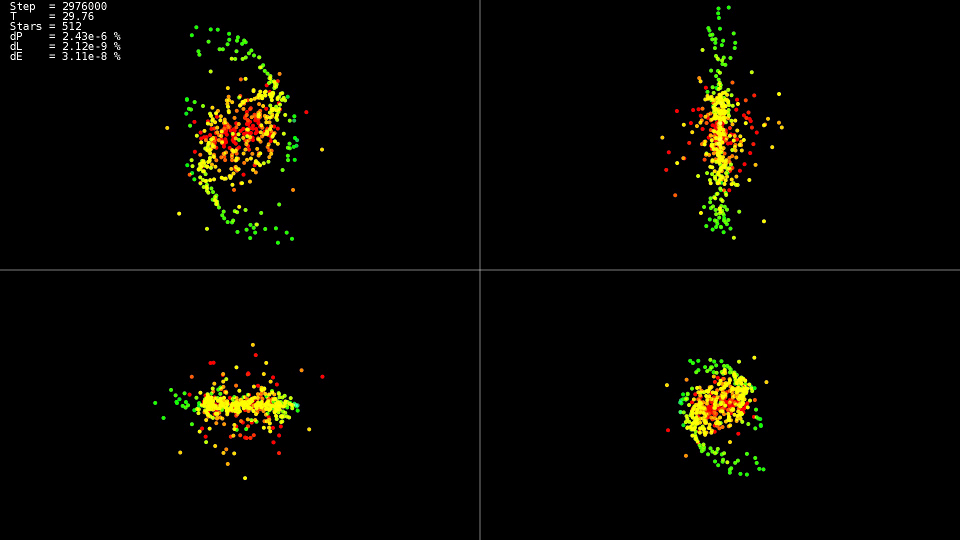
I wonder what happened to the system at these moments
| Video 1. Modeling a system of 512 bodies. Dorman-Prince Method. Dynamic step |
The video demonstrates that up to the point in time
Total
For the solution, it is better to use nested methods that allow you to dynamically control the integration step, and reduce it only on "complex" sections of the trajectory.
Do not chase the highest order methods. Even when using the data type 'double', they do not reach their potential capabilities, using the data types with greater accuracy greatly increases the time it takes to solve the problem.
CPU implementation
Now that the choice of a method for solving equations is defined, let us try to figure out the calculation of the interaction force for each particle. We get a double cycle for all particles:
Implementation code 'simple'
for(size_t body1 = 0; body1 < count; ++body1)
{
const nbvertex_t v1(rx[ body1 ], ry[ body1 ], rz[ body1 ]);
nbvertex_t total_force;
for(size_t body2 = 0; body2 != count; ++body2)
{
if(body1 == body2)
{
continue;
}
const nbvertex_t v2(rx[ body2 ], ry[ body2 ], rz[ body2 ]);
const nbvertex_t force(m_data->force(v1, v2, mass[body1], mass[body2]));
total_force += force;
}
frx[body1] = vx[body1];
fry[body1] = vy[body1];
frz[body1] = vz[body1];
fvx[body1] = total_force.x / mass[body1];
fvy[body1] = total_force.y / mass[body1];
fvz[body1] = total_force.z / mass[body1];
}
The gravitational forces for each body are calculated independently, and to use all the processor cores, it is enough to write the OpenMP directive before the first cycle:
A piece of code from the implementation of 'openmp'
#pragma omp parallel for
for(size_t body1 = 0; body1 < count; ++body1)
Because Since each body interacts with each, to reduce the number of processor interactions with RAM and improve cache usage, we have the ability to load part of the data into the cache and use it repeatedly:
Implementation code 'openmp + block'
#pragma omp parallel for
for(size_t n1 = 0; n1 < count; n1 += BLOCK_SIZE)
{
nbcoord_t x1[BLOCK_SIZE];
nbcoord_t y1[BLOCK_SIZE];
nbcoord_t z1[BLOCK_SIZE];
nbcoord_t m1[BLOCK_SIZE];
nbvertex_t total_force[BLOCK_SIZE];
for(size_t b1 = 0; b1 != BLOCK_SIZE; ++b1)
{
size_t local_n1 = b1 + n1;
x1[b1] = rx[local_n1];
y1[b1] = ry[local_n1];
z1[b1] = rz[local_n1];
m1[b1] = mass[local_n1];
}
for(size_t n2 = 0; n2 < count; n2 += BLOCK_SIZE)
{
nbcoord_t x2[BLOCK_SIZE];
nbcoord_t y2[BLOCK_SIZE];
nbcoord_t z2[BLOCK_SIZE];
nbcoord_t m2[BLOCK_SIZE];
for(size_t b2 = 0; b2 != BLOCK_SIZE; ++b2)
{
size_t local_n2 = b2 + n2;
x2[b2] = rx[local_n2];
y2[b2] = ry[local_n2];
z2[b2] = rz[local_n2];
m2[b2] = mass[n2 + b2];
}
for(size_t b1 = 0; b1 != BLOCK_SIZE; ++b1)
{
const nbvertex_t v1(x1[ b1 ], y1[ b1 ], z1[ b1 ]);
for(size_t b2 = 0; b2 != BLOCK_SIZE; ++b2)
{
const nbvertex_t v2(x2[ b2 ], y2[ b2 ], z2[ b2 ]);
const nbvertex_t force(m_data->force(v1, v2, m1[b1], m2[b2]));
total_force[b1] += force;
}
}
}
for(size_t b1 = 0; b1 != BLOCK_SIZE; ++b1)
{
size_t local_n1 = b1 + n1;
frx[local_n1] = vx[local_n1];
fry[local_n1] = vy[local_n1];
frz[local_n1] = vz[local_n1];
fvx[local_n1] = total_force[b1].x / m1[b1];
fvy[local_n1] = total_force[b1].y / m1[b1];
fvz[local_n1] = total_force[b1].z / m1[b1];
}
}
Further optimization consists in taking out the contents of the function of calculating the force in the main cycle and eliminating division and multiplication by body mass m1 [b1]. Besides the fact that we have reduced the calculations a little, the compiler will be able to apply vector instructions of the SSE and AVX processor on such an expanded cycle.
Implementation code 'openmp + block + optimization'
#pragma omp parallel for
for(size_t n1 = 0; n1 < count; n1 += BLOCK_SIZE)
{
nbcoord_t x1[BLOCK_SIZE];
nbcoord_t y1[BLOCK_SIZE];
nbcoord_t z1[BLOCK_SIZE];
nbcoord_t total_force_x[BLOCK_SIZE];
nbcoord_t total_force_y[BLOCK_SIZE];
nbcoord_t total_force_z[BLOCK_SIZE];
for(size_t b1 = 0; b1 != BLOCK_SIZE; ++b1)
{
size_t local_n1 = b1 + n1;
x1[b1] = rx[local_n1];
y1[b1] = ry[local_n1];
z1[b1] = rz[local_n1];
total_force_x[b1] = 0;
total_force_y[b1] = 0;
total_force_z[b1] = 0;
}
for(size_t n2 = 0; n2 < count; n2 += BLOCK_SIZE)
{
nbcoord_t x2[BLOCK_SIZE];
nbcoord_t y2[BLOCK_SIZE];
nbcoord_t z2[BLOCK_SIZE];
nbcoord_t m2[BLOCK_SIZE];
for(size_t b2 = 0; b2 != BLOCK_SIZE; ++b2)
{
size_t local_n2 = b2 + n2;
x2[b2] = rx[local_n2];
y2[b2] = ry[local_n2];
z2[b2] = rz[local_n2];
m2[b2] = mass[n2 + b2];
}
for(size_t b1 = 0; b1 != BLOCK_SIZE; ++b1)
{
for(size_t b2 = 0; b2 != BLOCK_SIZE; ++b2)
{
nbcoord_t dx = x1[b1] - x2[b2];
nbcoord_t dy = y1[b1] - y2[b2];
nbcoord_t dz = z1[b1] - z2[b2];
nbcoord_t r2(dx * dx + dy * dy + dz * dz);
if(r2 < NBODY_MIN_R)
{
r2 = NBODY_MIN_R;
}
nbcoord_t r = sqrt(r2);
nbcoord_t coeff = (m2[b2]) / (r * r2);
dx *= coeff;
dy *= coeff;
dz *= coeff;
total_force_x[b1] -= dx;
total_force_y[b1] -= dy;
total_force_z[b1] -= dz;
}
}
}
for(size_t b1 = 0; b1 != BLOCK_SIZE; ++b1)
{
size_t local_n1 = b1 + n1;
frx[local_n1] = vx[local_n1];
fry[local_n1] = vy[local_n1];
frz[local_n1] = vz[local_n1];
fvx[local_n1] = total_force_x[b1];
fvy[local_n1] = total_force_y[b1];
fvz[local_n1] = total_force_z[b1];
}
}
Table 2. Dependence of the calculation time (in seconds) of the function
| 2048 | 4096 | 8192 | 16384 | 32768 | |
|---|---|---|---|---|---|
| simple | 0.0425 | 0.1651 | 0.6594 | 2.65 | 10.52 |
| openmp | 0.0078 | 0.0260 | 0.1079 | 0.417 | 1.655 |
| openmp + block + optimization | 0.0037 | 0.0128 | 0.0495 | 0.194 | 0.774 |
System Parameters:
- system: Debian 9, Intel Core i7-5820K (6 core)
- compiler: gcc 6.3.0
It is clearly seen that the version with OpenMP support is accelerated by six times, exactly in terms of the number of cores, and the optimized version is faster by a little more than two times. So, with optimization, you should not rely only on concurrency. Interestingly, in single-stream calculations, the processor worked at a frequency of 3.6 GHz, in the parallel version (openmp) it dropped the frequency to 3.4 GHz, and in the parallel and optimized (openmp + block + optimization) it dropped to 3.3 GHz, but this it did not stop her from working 13.6 times faster. It is also seen that an increase in the computation time with an increase in the size of the problem is quadratic, and a further increase
GPU implementation
But there is a desire to make calculations even faster. There are several directions available for acceleration: GPU computation, function approximation
Opencl
To get started with OpenCL, you need to get a list of available platforms. The most common platforms are AMD, Intel, and NVidia.
The code
std::vector platforms;
cl::Platform::get(&platforms);
Next, after choosing a platform, you need to select the computing device that this platform represents:
The code
const cl::Platform& platform(platforms[platform_n]);
std::vector all_devices;
platform.getDevices(CL_DEVICE_TYPE_ALL, &all_devices);
And at the end of the preparatory phase, it is necessary to create a context and queues within which memory will be allocated and calculations will be performed. For example, a context that combines all the computing devices of a selected platform is created as follows:
Context and Queue Creation Code
cl::Context context(all_devices);
std::vector queues;
for(cl::Device device: all_devices)
queues.push_back(cl::CommandQueue(context, device));
To download the source code to a computing device, it must be compiled, the cl :: Program class is intended for this.
Kernel compilation code
std::vector< std::string > source_data;
cl::Program::Sources sources;
for(int i = 0; i != files.size(); ++i)
{
source_data.push_back(load_program(files[i]));//Загружаем из файла
sources.push_back(std::make_pair(source_data.back().data(),
source_data.back().size()));
}
cl::Program prog(context, sources);
devices.push_back(all_devices);
prog.build(devices, options);
To describe the parameters of a function (kernel) that is executed on a computing device, there is a cl template: make_kernel.
Interaction strength calculation kernel example
typedef cl::make_kernel< cl_int, cl_int, //Block offset
cl::Buffer, //mass
cl::Buffer, //y
cl::Buffer, //f
cl_int, cl_int, //yoff,foff
cl_int, cl_int //points_count,stride
> ComputeBlock;
Further, everything is simple: we declare a variable with the type of the kernel, pass the compiled program and the name of the computational kernel into it, we can start the kernel almost like a normal function.
Kernel Launch Code
ComputeBlock fcompute(prog, "ComputeBlockLocal");
cl::NDRange global_range(device_data_size);
cl::NDRange local_range(block_size);
cl::EnqueueArgs eargs(ctx.m_queue, global_range, local_range);
fcompute(eargs, ...все остальные аргументы); //Собственно, сам вызов ядра.
The computational core for OpenCL itself is very similar to the 'openmp + block + optimization' option for the CPU, only in contrast to the CPU version, the first cycle is controlled using OpenCL (the cycle range is determined by the global_range variable from the kernel launch code, and the current iteration number is available from the kernel using the function get_global_id (0)). First, part of the body data is loaded from local memory, then processed. Local memory is common to all threads in the group, so the download occurs once for the group, and is processed by each thread in the group and, since local memory is much faster than global, calculations are much faster.
Kernel code
__kernel void ComputeBlockLocal(int offset_n1, int offset_n2,
__global const nbcoord_t* mass,
__global const nbcoord_t* y,
__global nbcoord_t* f, int yoff,
int foff, int points_count, int stride)
{
int n1 = get_global_id(0) + offset_n1;
__global const nbcoord_t* rx = y + yoff;
__global const nbcoord_t* ry = rx + stride;
__global const nbcoord_t* rz = rx + 2 * stride;
__global const nbcoord_t* vx = rx + 3 * stride;
__global const nbcoord_t* vy = rx + 4 * stride;
__global const nbcoord_t* vz = rx + 5 * stride;
__global nbcoord_t* frx = f + foff;
__global nbcoord_t* fry = frx + stride;
__global nbcoord_t* frz = frx + 2 * stride;
__global nbcoord_t* fvx = frx + 3 * stride;
__global nbcoord_t* fvy = frx + 4 * stride;
__global nbcoord_t* fvz = frx + 5 * stride;
nbcoord_t x1 = rx[n1];
nbcoord_t y1 = ry[n1];
nbcoord_t z1 = rz[n1];
nbcoord_t res_x = 0.0;
nbcoord_t res_y = 0.0;
nbcoord_t res_z = 0.0;
__local nbcoord_t x2[NBODY_DATA_BLOCK_SIZE];
__local nbcoord_t y2[NBODY_DATA_BLOCK_SIZE];
__local nbcoord_t z2[NBODY_DATA_BLOCK_SIZE];
__local nbcoord_t m2[NBODY_DATA_BLOCK_SIZE];
// NB! get_local_size(0) == NBODY_DATA_BLOCK_SIZE
for(int b2 = 0; b2 < points_count; b2 += NBODY_DATA_BLOCK_SIZE)
{
int n2 = b2 + offset_n2 + get_local_id(0);
// Copy data block to local memory
x2[ get_local_id(0) ] = rx[n2];
y2[ get_local_id(0) ] = ry[n2];
z2[ get_local_id(0) ] = rz[n2];
m2[ get_local_id(0) ] = mass[n2];
// Synchronize local work-items copy operations
barrier(CLK_LOCAL_MEM_FENCE);
nbcoord_t local_res_x = 0.0;
nbcoord_t local_res_y = 0.0;
nbcoord_t local_res_z = 0.0;
for(int local_n2 = 0; local_n2 != NBODY_DATA_BLOCK_SIZE; ++local_n2)
{
nbcoord_t dx = x1 - x2[local_n2];
nbcoord_t dy = y1 - y2[local_n2];
nbcoord_t dz = z1 - z2[local_n2];
nbcoord_t r2 = (dx * dx + dy * dy + dz * dz);
if(r2 < NBODY_MIN_R)
{
r2 = NBODY_MIN_R;
}
nbcoord_t r = sqrt(r2);
nbcoord_t coeff = (m2[local_n2]) / (r * r2);
dx *= coeff;
dy *= coeff;
dz *= coeff;
local_res_x -= dx;
local_res_y -= dy;
local_res_z -= dz;
}
// Synchronize local work-items computations
barrier(CLK_LOCAL_MEM_FENCE);
res_x += local_res_x;
res_y += local_res_y;
res_z += local_res_z;
}
frx[n1] = vx[n1];
fry[n1] = vy[n1];
frz[n1] = vz[n1];
fvx[n1] = res_x;
fvy[n1] = res_y;
fvz[n1] = res_z;
}
Cuda
The implementation for the NVidia CUDA platform is a bit simpler than OpenCL, we don’t need to create the device context and manage the execution queue (at least until we want to make a multi-GPU implementation). As in the case of OpenCL, we need to allocate memory on the GPU, copy our data into it, and then we can start the computing core.
You can read more about working with CUDA here .
CUDA Kernel Launch Code
dim3 grid(count / block_size);
dim3 block(block_size);
size_t shared_size(4 * sizeof(nbcoord_t) * block_size);
kfcompute <<< grid, block, shared_size >>> (...параметры ядра...);
Unlike OpenCL, CUDA does not specify the full range of iterations (in the OpenCL implementation it is global_range), but sets the grid size and block sizes in the grid, accordingly, the calculation of the current body number changes slightly, otherwise the kernel is very similar to OpenCL, with the exception of other names synchronization and specifier functions for shared memory. Another useful distinguishing feature of CUDA is that we can specify the required size of shared memory when the kernel starts. As in the OpenCL implementation, at the beginning of each iteration block we copy part of the data into shared memory and then work with this memory from all the threads of the block.
CUDA kernel code
__global__ void kfcompute(int offset_n2, const nbcoord_t* y, int yoff, nbcoord_t* f, int foff,
const nbcoord_t* mass, int points_count, int stride)
{
int n1 = blockDim.x * blockIdx.x + threadIdx.x;
const nbcoord_t* rx = y + yoff;
const nbcoord_t* ry = rx + stride;
const nbcoord_t* rz = rx + 2 * stride;
nbcoord_t x1 = rx[n1];
nbcoord_t y1 = ry[n1];
nbcoord_t z1 = rz[n1];
nbcoord_t res_x = 0.0;
nbcoord_t res_y = 0.0;
nbcoord_t res_z = 0.0;
extern __shared__ nbcoord_t shared_xyzm_buf[];
nbcoord_t* x2 = shared_xyzm_buf;
nbcoord_t* y2 = x2 + blockDim.x;
nbcoord_t* z2 = y2 + blockDim.x;
nbcoord_t* m2 = z2 + blockDim.x;
for(int b2 = 0; b2 < points_count; b2 += blockDim.x)
{
int n2 = b2 + offset_n2 + threadIdx.x;
// Copy data block to local memory
x2[ threadIdx.x ] = rx[n2];
y2[ threadIdx.x ] = ry[n2];
z2[ threadIdx.x ] = rz[n2];
m2[ threadIdx.x ] = mass[n2];
// Synchronize local work-items copy operations
__syncthreads();
nbcoord_t local_res_x = 0.0;
nbcoord_t local_res_y = 0.0;
nbcoord_t local_res_z = 0.0;
for(int n2 = 0; n2 != blockDim.x; ++n2)
{
nbcoord_t dx = x1 - x2[n2];
nbcoord_t dy = y1 - y2[n2];
nbcoord_t dz = z1 - z2[n2];
nbcoord_t r2 = (dx * dx + dy * dy + dz * dz);
if(r2 < NBODY_MIN_R)
{
r2 = NBODY_MIN_R;
}
nbcoord_t r = sqrt(r2);
nbcoord_t coeff = (m2[n2]) / (r * r2);
dx *= coeff;
dy *= coeff;
dz *= coeff;
local_res_x -= dx;
local_res_y -= dy;
local_res_z -= dz;
}
// Synchronize local work-items computations
__syncthreads();
res_x += local_res_x;
res_y += local_res_y;
res_z += local_res_z;
}
n1 += foff;
f[n1 + 3 * stride] = res_x;
f[n1 + 4 * stride] = res_y;
f[n1 + 5 * stride] = res_z;
}
Table 3. The dependence of the calculation time (in seconds) function
| 4096 | 8192 | 16384 | 32768 | 65536 | 131072 | |
|---|---|---|---|---|---|---|
| openmp + block + optimization | 0.0128 | 0.0495 | 0.194 | 0.774 | --- | --- |
| OpenCL + half NVidia K80 | 0.004 | 0.008 | 0.026 | 0.134 | 0.322 | 1.18 |
| CUDA + half NVidia K80 | 0.004 | 0.008 | 0.0245 | 0.115 | 0.291 | 1.13 |
Where to get NVidia K80
In general, the result is disappointing, only 5-6 times faster than the CPU implementation. Even if we conduct calculations on the entire K80, we will get acceleration up to 12 times, but since Since the complexity of the task is quadratic, then in a reasonable time we will be able to process not 32768 interacting bodies, but 131072, which is only 4 times more.
Function Approximation 
If you look closely at the function, which is set by the attractive force of two bodies, it is clear that it decreases quadratically with distance. Therefore, we can accurately calculate the force of interaction between close bodies, and approximately between distant ones. One well-known approach
is the treecode algorithm proposed by D. Barnes and P. Hat. Octo- tree is being built in the simulated spacecontaining in its leaves the coordinates and masses of the modeled bodies. The parent nodes contain the center of mass, the total mass of the child nodes and the radius of the sphere described around the bodies of the child nodes. The root of the tree contains the center of mass of all bodies, their total mass and the radius of the sphere described around them. When calculating the interaction force, the distance to the root of the tree is first considered if the ratio of the distance to the node to its radius is greater than some constant
In my approach, I decided not to use the octree tree , but the kd tree, because it is easier to use and has lower storage overhead compared to the octree.
Let's go back to the implementation on the CPU. A kd-tree node can be represented in the form of a class containing pointers to the left and right descendants and information about the coordinates and mass:
Kd tree node
class node
{
node* m_left; //!< Левый потомок
node* m_right; //!< Правый потомок
nbvertex_t m_mass_center; //!< Координаты центра масс узла
nbcoord_t m_mass; //!< Масса узла
nbcoord_t m_radius_sqr; //!< Квадрат радиуса описанной сферы, умноженный на lambda_crit
nbvertex_t m_bmin; //!< Минимальные координаты описанного бокса
nbvertex_t m_bmax; //!< Максимальные координаты описанного бокса
size_t m_body_n; //!< Номер тела, связанного с узлом
};
With this method of storing the tree, we have two possible options for traversing the tree: either use explicit recursion, or use the stack ourselves. I settled on the second option.
Calculation of the interaction force by traversing a tree
nbvertex_t force_compute(const nbvertex_t& v1,
const nbcoord_t mass1)
{
nbvertex_t total_force;
node* stack_data[MAX_STACK_SIZE] = {};
node** stack = stack_data;
node** stack_head = stack;
*stack++ = m_root;
while(stack != stack_head)
{
node* curr = *--stack;
const nbcoord_t distance_sqr((v1 - curr->m_mass_center).norm());
if(distance_sqr > curr->m_radius_sqr)
{//Узел достаточно далеко, вычисляем силу и пропускаем его детей
total_force += force(v1, curr->m_mass_center, mass1, curr->m_mass);
}
else
{// Узел слишком близко, запоминаем детей для последующей обработки
if(curr->m_right != NULL)
{
*stack++ = curr->m_right;
}
if(curr->m_left != NULL)
{
*stack++ = curr->m_left;
}
}
}
return total_force;
}
As in the case of the “exact” CPU implementation, the force calculation function is called for each body. The cycle across all bodies can be easily parallelized using OpenMP directives.
But neighboring loop iterations in this case will refer to completely different parts of the tree, which does not allow efficient use of the processor cache. To overcome this problem, all bodies need to be traversed not in the original order, but in the order in which the bodies are located in the leaves of the kd-tree, then neighboring iterations will occur for bodies that are close in space, and will traverse the tree along almost the same paths.
Tree leaf traversal
template
void traverse(Visitor visit)
{
node* stack_data[MAX_STACK_SIZE] = {};
node** stack = stack_data;
node** stack_head = stack;
*stack++ = m_root;
while(stack != stack_head)
{
node* curr = *--stack;
if(curr->m_radius_sqr > 0)
{//Это не лист. Откладываем детей на стек.
if(curr->m_left != NULL)
{
*stack++ = curr->m_left;
}
if(curr->m_right != NULL)
{
*stack++ = curr->m_right;
}
}
else
{// Это листовой узел. Вычисляем силу.
visit(curr->m_body_n, curr->m_mass_center, curr->m_mass);
}
}
}
This implementation has another problem - there is no universal way to parallelize such a tree traversal. But we can completely change the way the tree is stored in memory - we can store all the nodes in one linear array and completely abandon the storage of pointers to descendants, by analogy with the construction of a binary heap . When starting the numbering of nodes with
Calculation of force by traversing a tree in an array
nbvertex_t force_compute(const nbvertex_t& v1, const nbcoord_t mass1)
{
nbvertex_t total_force;
size_t stack_data[MAX_STACK_SIZE] = {};
size_t* stack = stack_data;
size_t* stack_head = stack;
*stack++ = NBODY_HEAP_ROOT_INDEX;
while(stack != stack_head)
{
size_t curr = *--stack;
const nbcoord_t distance_sqr((v1 - m_mass_center[curr]).norm());
if(distance_sqr > m_radius_sqr[curr])
{
total_force += force(v1, m_mass_center[curr], mass1, m_mass[curr]);
}
else
{
size_t left(left_idx(curr));
size_t rght(rght_idx(curr));
if(rght < m_body_n.size())
{
*stack++ = rght;
}
if(left < m_body_n.size())
{
*stack++ = left;
}
}
}
return total_force;
}
But this is not all the possibilities that storing the nodes in the array opens up to us - we can refuse the stack when crawling. To do this, in the code branch in which we go to the children of the node, we add the function to calculate the next node (
To skip the current subtree, we need to go down to the root (direction
Subtree Skip Function Code
index_t skip_down(index_t idx)
{
// While index is 'right' -> go down
while(is_right(idx))
{
index_t parent = parent_idx(idx);
// We at root again. Stop traverse.
if(parent == NBODY_HEAP_ROOT_INDEX)
{
return NBODY_HEAP_ROOT_INDEX;
}
idx = parent;
}
return left2right(idx);
}
Figure 8. Skipping a subtree
To go to the next node, if possible, go to the left child (direction
Go to next node function code
index_t next_up(index_t idx, index_t tree_size)
{
index_t left = left_idx(idx);
if(left < tree_size)
{
return left;
}
return skip_down(idx);
}
Figure 9. Transitions to the next node
It might seem that we replaced the recursion with a loop
Optimized Skip Subtree Function Code
index_t skip_down(index_t idx)
{
idx = idx >> (__builtin_ffs(~idx) - 1);
return left2right(idx);
}
After that, we can exclude the stack from the tree traversal function and replace it with a pair
Calculation of force by traversing a tree in an array without using a stack
nbvertex_t force_compute(const nbvertex_t& v1,
const nbcoord_t mass1) const
{
nbvertex_t total_force;
size_t curr = NBODY_HEAP_ROOT_INDEX;
size_t tree_size = m_mass_center.size();
do
{
const nbcoord_t distance_sqr((v1 - m_mass_center[curr]).norm());
if(distance_sqr > m_radius_sqr[curr])
{
total_force += force(v1, m_mass_center[curr], mass1, m_mass[curr]);
curr = skip_down(curr);
}
else
{
curr = next_up(curr, tree_size);
}
}
while(curr != NBODY_HEAP_ROOT_INDEX);
return total_force;
}
In total, we got six combinations of tree traversal and force calculation. Compare these approaches in terms of computation time and quality. We take as a measure of quality the relative change in the total energy of the system after 100 iterations. As a model system, we take two interacting “galaxies” consisting of
Table 4. Combinations of tree traversal method and force calculation
| Tree traversal / force calculation type | Tree with stack | 'Pile' with a stack | 'Heap' without a stack |
|---|---|---|---|
| Iterations by body number | cycle + tree | cycle + heap | cycle + heapstackless |
| Leaf bypass | nestedtree + tree | nestedtree + heap | nestedtree + heapstackless |
It can be seen that the implementation of 'nestedtree + tree' is hopelessly behind in speed, because it lacks concurrency. Implementations with the location of tree nodes in the array and indexing as in a binary heap are in the lead. The relative change in energy is negligible for all variants with
GPU tree traversal
I tried to bypass the tree on the GPU using both OpenCL technology and CUDA. The option of storing nodes in the form of a tree was immediately discarded, and only the options were left with storing the tree in an array with indexing as in a binary heap. In general, the implementation of the computing core is not much different from the CPU version.
OpenCL kernel for computing strength by traversing a tree (traversal in the order of numbering bodies)
__kernel void ComputeTreeBH(int offset_n1, int points_count, int tree_size,
__global const nbcoord_t* y,
__global nbcoord_t* f,
__global const nbcoord_t* tree_cmx,
__global const nbcoord_t* tree_cmy,
__global const nbcoord_t* tree_cmz,
__global const nbcoord_t* tree_mass,
__global const nbcoord_t* tree_crit_r2)
{
int n1 = get_global_id(0) + offset_n1;
int stride = points_count;
__global const nbcoord_t* rx = y;
__global const nbcoord_t* ry = rx + stride;
__global const nbcoord_t* rz = rx + 2 * stride;
__global const nbcoord_t* vx = rx + 3 * stride;
__global const nbcoord_t* vy = rx + 4 * stride;
__global const nbcoord_t* vz = rx + 5 * stride;
__global nbcoord_t* frx = f;
__global nbcoord_t* fry = frx + stride;
__global nbcoord_t* frz = frx + 2 * stride;
__global nbcoord_t* fvx = frx + 3 * stride;
__global nbcoord_t* fvy = frx + 4 * stride;
__global nbcoord_t* fvz = frx + 5 * stride;
nbcoord_t x1 = rx[n1];
nbcoord_t y1 = ry[n1];
nbcoord_t z1 = rz[n1];
nbcoord_t res_x = 0.0;
nbcoord_t res_y = 0.0;
nbcoord_t res_z = 0.0;
int stack_data[MAX_STACK_SIZE] = {};
int stack = 0;
int stack_head = stack;
stack_data[stack++] = NBODY_HEAP_ROOT_INDEX;
while(stack != stack_head)
{
int curr = stack_data[--stack];
nbcoord_t dx = x1 - tree_cmx[curr];
nbcoord_t dy = y1 - tree_cmy[curr];
nbcoord_t dz = z1 - tree_cmz[curr];
nbcoord_t r2 = (dx * dx + dy * dy + dz * dz);
if(r2 > tree_crit_r2[curr])
{
if(r2 < NBODY_MIN_R)
{
r2 = NBODY_MIN_R;
}
nbcoord_t r = sqrt(r2);
nbcoord_t coeff = tree_mass[curr] / (r * r2);
dx *= coeff;
dy *= coeff;
dz *= coeff;
res_x -= dx;
res_y -= dy;
res_z -= dz;
}
else
{
int left = left_idx(curr);
int rght = rght_idx(curr);
if(left < tree_size)
{
stack_data[stack++] = left;
}
if(rght < tree_size)
{
stack_data[stack++] = rght;
}
}
}
frx[n1] = vx[n1];
fry[n1] = vy[n1];
frz[n1] = vz[n1];
fvx[n1] = res_x;
fvy[n1] = res_y;
fvz[n1] = res_z;
}
In the first version, tree traversal began in the order of numbering the bodies in the original array, so neighboring threads bypassed completely different parts of the tree, which negatively affected the performance of the GPU memory cache. Therefore, in the second embodiment, a traversal was applied, starting from the top of the tree, in this case, neighboring threads begin to traverse the tree along the same path, because neighboring tree tops are nearby and in space. It is also important that we chose numbering in the array of tree nodes not from scratch, but from one, in this case the leaves of the tree are stored in the second half of the array, and with the number of bodies equal to the power of two, we will have equal access to memory by index tn1.
OpenCL kernel for calculating strength by traversing a tree (traversing the numbering nodes of a tree)
__kernel void ComputeHeapBH(int offset_n1, int points_count, int tree_size,
__global const nbcoord_t* y,
__global nbcoord_t* f,
__global const nbcoord_t* tree_cmx,
__global const nbcoord_t* tree_cmy,
__global const nbcoord_t* tree_cmz,
__global const nbcoord_t* tree_mass,
__global const nbcoord_t* tree_crit_r2,
__global const int* body_n)
{
int tree_offset = points_count - 1 + NBODY_HEAP_ROOT_INDEX;
int stride = points_count;
int tn1 = get_global_id(0) + offset_n1 + tree_offset;
int n1 = body_n[tn1];
nbcoord_t x1 = tree_cmx[tn1];
nbcoord_t y1 = tree_cmy[tn1];
nbcoord_t z1 = tree_cmz[tn1];
nbcoord_t res_x = 0.0;
nbcoord_t res_y = 0.0;
nbcoord_t res_z = 0.0;
int stack_data[MAX_STACK_SIZE] = {};
int stack = 0;
int stack_head = stack;
stack_data[stack++] = NBODY_HEAP_ROOT_INDEX;
while(stack != stack_head)
{
int curr = stack_data[--stack];
nbcoord_t dx = x1 - tree_cmx[curr];
nbcoord_t dy = y1 - tree_cmy[curr];
nbcoord_t dz = z1 - tree_cmz[curr];
nbcoord_t r2 = (dx * dx + dy * dy + dz * dz);
if(r2 > tree_crit_r2[curr])
{
if(r2 < NBODY_MIN_R)
{
r2 = NBODY_MIN_R;
}
nbcoord_t r = sqrt(r2);
nbcoord_t coeff = tree_mass[curr] / (r * r2);
dx *= coeff;
dy *= coeff;
dz *= coeff;
res_x -= dx;
res_y -= dy;
res_z -= dz;
}
else
{
int left = left_idx(curr);
int rght = rght_idx(curr);
if(left < tree_size)
{
stack_data[stack++] = left;
}
if(rght < tree_size)
{
stack_data[stack++] = rght;
}
}
}
__global const nbcoord_t* vx = y + 3 * stride;
__global const nbcoord_t* vy = y + 4 * stride;
__global const nbcoord_t* vz = y + 5 * stride;
__global nbcoord_t* frx = f;
__global nbcoord_t* fry = frx + stride;
__global nbcoord_t* frz = frx + 2 * stride;
__global nbcoord_t* fvx = frx + 3 * stride;
__global nbcoord_t* fvy = frx + 4 * stride;
__global nbcoord_t* fvz = frx + 5 * stride;
frx[n1] = vx[n1];
fry[n1] = vy[n1];
frz[n1] = vz[n1];
fvx[n1] = res_x;
fvy[n1] = res_y;
fvz[n1] = res_z;
}
When traversing the order of numbering of tree nodes, we got a performance increase. But this option can also be improved. The global memory in which the tree nodes are currently located is optimized for shared access., i.e. threads of one group should read words located in one memory block. In our case, the tree traversal starts along the same paths, and we request the same data with all the threads of the group, but the further we go deeper into the tree, the paths of neighboring threads diverge more and more, and we have to request different data, which reduces the performance of the subsystem several times memory. But the nodes of each subtree belonging to the same level are located in relatively close memory cells. Those. when traversing the rest of the tree, the neighboring threads of the computing core do not access the same nodes of the tree, but closely located in memory. To optimize this memory access, texture memory can be used. But there is one snag. At the moment, textures do not support working with double precision data (we want to accurately calculate). But in CUDA there is a function__hiloint2double , which collects a double-precision number from two integers.
Double precision number request code from a texture storing integers
template<>
struct nb1Dfetch
{
typedef double4 vec4;
static __device__ double fetch(cudaTextureObject_t tex, int i)
{
int2 p(tex1Dfetch(tex, i));
return __hiloint2double(p.y, p.x);
}
static __device__ vec4 fetch4(cudaTextureObject_t tex, int i)
{
int ii(2 * i);
int4 p1(tex1Dfetch(tex, ii));
int4 p2(tex1Dfetch(tex, ii + 1));
vec4 d4 = {__hiloint2double(p1.y, p1.x),
__hiloint2double(p1.w, p1.z),
__hiloint2double(p2.y, p2.x),
__hiloint2double(p2.w, p2.z)
};
return d4;
}
};
In this case, two implementations were made, in one each element of the tree (x, y, z, tree_crit_r2) was requested independently, and in the second implementation these requests were combined. The request for the mass of the node occurs much less frequently, only if the condition r2> tree_crit_r2 [curr] is fulfilled , so it makes no sense to combine this request with the others. Another useful feature of the CUDA framework is the ability to control the ratio of the sizes of the L1 cache and the size of shared memory ( cudaFuncSetCacheConfig ). In case of tree traversal, we do not use shared memory, so we can increase the L1 cache to the detriment of it.
CUDA kernel for calculating strength by traversing a tree (traversing the numbering order of tree nodes)
__global__ void kfcompute_heap_bh_tex(int offset_n1, int points_count, int tree_size,
nbcoord_t* f,
cudaTextureObject_t tree_xyzr,
cudaTextureObject_t tree_mass,
const int* body_n)
{
nb1Dfetch tex;
int tree_offset = points_count - 1 + NBODY_HEAP_ROOT_INDEX;
int stride = points_count;
int tn1 = blockDim.x * blockIdx.x + threadIdx.x + offset_n1 + tree_offset;
int n1 = body_n[tn1];
nbvec4_t xyzr = tex.fetch4(tree_xyzr, tn1);
nbcoord_t x1 = xyzr.x;
nbcoord_t y1 = xyzr.y;
nbcoord_t z1 = xyzr.z;
nbcoord_t res_x = 0.0;
nbcoord_t res_y = 0.0;
nbcoord_t res_z = 0.0;
int stack_data[MAX_STACK_SIZE] = {};
int stack = 0;
int stack_head = stack;
stack_data[stack++] = NBODY_HEAP_ROOT_INDEX;
while(stack != stack_head)
{
int curr = stack_data[--stack];
nbvec4_t xyzr2 = tex.fetch4(tree_xyzr, curr);
nbcoord_t dx = x1 - xyzr2.x;
nbcoord_t dy = y1 - xyzr2.y;
nbcoord_t dz = z1 - xyzr2.z;
nbcoord_t r2 = (dx * dx + dy * dy + dz * dz);
if(r2 > xyzr2.w)
{
if(r2 < NBODY_MIN_R)
{
r2 = NBODY_MIN_R;
}
nbcoord_t r = sqrt(r2);
nbcoord_t coeff = tex.fetch(tree_mass, curr) / (r * r2);
dx *= coeff;
dy *= coeff;
dz *= coeff;
res_x -= dx;
res_y -= dy;
res_z -= dz;
}
else
{
int left = nbody_heap_func::left_idx(curr);
int rght = nbody_heap_func::rght_idx(curr);
if(left < tree_size)
{
stack_data[stack++] = left;
}
if(rght < tree_size)
{
stack_data[stack++] = rght;
}
}
}
f[n1 + 3 * stride] = res_x;
f[n1 + 4 * stride] = res_y;
f[n1 + 5 * stride] = res_z;
}
An analysis of the program in the nvprof profiler showed that even when using texture memory to store a tree, there is still a very high load on global memory.
Indeed, in CUDA, all kernel memory that is addressed to 'calculated' addresses is stored in global memory, and accordingly, the stack that is needed to traverse the tree is located in global memory and eats away a significant part of the memory chip bandwidth, because the stack has each run thread, and there are a lot of threads.
But, fortunately, we already know how to traverse a tree without using a stack. Complementing the previous computational core with the functions of computing the next tree node, we get a new kernel, moreover, more compact.
CUDA ядро для вычисления силы путём обхода дерева без использования стека
__global__ void kfcompute_heap_bh_stackless(int offset_n1, int points_count, int tree_size,
nbcoord_t* f,
cudaTextureObject_t tree_xyzr,
cudaTextureObject_t tree_mass,
const int* body_n)
{
nb1Dfetch tex;
int tree_offset = points_count - 1 + NBODY_HEAP_ROOT_INDEX;
int stride = points_count;
int tn1 = blockDim.x * blockIdx.x + threadIdx.x + offset_n1 + tree_offset;
int n1 = body_n[tn1];
nbvec4_t xyzr = tex.fetch4(tree_xyzr, tn1);
nbcoord_t x1 = xyzr.x;
nbcoord_t y1 = xyzr.y;
nbcoord_t z1 = xyzr.z;
nbcoord_t res_x = 0.0;
nbcoord_t res_y = 0.0;
nbcoord_t res_z = 0.0;
int curr = NBODY_HEAP_ROOT_INDEX;
do
{
nbvec4_t xyzr2 = tex.fetch4(tree_xyzr, curr);
nbcoord_t dx = x1 - xyzr2.x;
nbcoord_t dy = y1 - xyzr2.y;
nbcoord_t dz = z1 - xyzr2.z;
nbcoord_t r2 = (dx * dx + dy * dy + dz * dz);
if(r2 > xyzr2.w)
{
if(r2 < NBODY_MIN_R)
{
r2 = NBODY_MIN_R;
}
nbcoord_t r = sqrt(r2);
nbcoord_t coeff = tex.fetch(tree_mass, curr) / (r * r2);
dx *= coeff;
dy *= coeff;
dz *= coeff;
res_x -= dx;
res_y -= dy;
res_z -= dz;
curr = nbody_heap_func::skip_idx(curr);
}
else
{
curr = nbody_heap_func::next_up(curr, tree_size);
}
}
while(curr != NBODY_HEAP_ROOT_INDEX);
f[n1 + 3 * stride] = res_x;
f[n1 + 4 * stride] = res_y;
f[n1 + 5 * stride] = res_z;
}
The performance of the cores running on the GPU is highly dependent on the size of the blocks into which we divide the task. Depends on this size how many registers, local memory and other resources will be available for each computing thread. You also need to keep in mind that while waiting for memory access in one thread, another thread can perform calculations on the shader processor, thus, with a sufficient number of simultaneously executed threads on one processor, the memory access time will be hidden behind the calculations. Therefore, before comparing the performance of our cores, we need to calculate the optimal block size for each of them. Let's make a comparison on the half available to us from NVidia K80.
Table 5. The dependence of the calculation time (in seconds) function
| Размер блока/ядро | 8 | 16 | 32 | 64 | 128 | 256 | 512 | 1024 |
|---|---|---|---|---|---|---|---|---|
| opencl+dense | 5.77 | 2.84 | 1.46 | 1.13 | 1.15 | 1.14 | 1.14 | 1.13 |
| cuda+dense | 5.44 | 2.55 | 1.27 | 0.96 | 0.97 | 0.99 | 0.99 | - |
| opencl+heap+cycle | 5.88 | 5.65 | 5.74 | 5.96 | 5.37 | 5.38 | 5.35 | 5.38 |
| opencl+heap+nested | 4.54 | 3.68 | 3.98 | 5.25 | 5.46 | 5.41 | 5.48 | 5.31 |
| cuda+heap+nested | 3.62 | 2.81 | 2.68 | 4.26 | 4.84 | 4.75 | 4.8 | 4.67 |
| cuda+heap+nested+tex | 2.6 | 1.51 | 0.912 | 0.7 | 1.85 | 1.75 | 1.69 | 1.61 |
| cuda+heap+nested+tex+stackless | 2.3 | 1.29 | 0.773 | 0.5 | 0.51 | 0.52 | 0.52 | 0.52 |
Таблица 6. Зависимость времени вычисления (в секундах) функции
| Размер блока/ядро | 8 | 16 | 32 | 64 | 128 | 256 | 512 | 1024 |
|---|---|---|---|---|---|---|---|---|
| opencl+dense | 366 | 179 | 89.9 | 69.3 | 70.3 | 69.1 | 68.9 | 68.0 |
| cuda+dense | 346 | 162 | 79.6 | 60.8 | 60.8 | 60.7 | 59.6 | - |
| opencl+heap+cycle | 16.2 | 18.2 | 20.1 | 21.2 | 21.2 | 21.3 | 21.2 | 21.1 |
| opencl+heap+nested | 10.5 | 7.63 | 6.38 | 8.23 | 9.95 | 9.89 | 9.65 | 9.66 |
| cuda+heap+nested | 8.67 | 6.44 | 5.39 | 5.93 | 8.65 | 8.61 | 8.41 | 8.27 |
| cuda+heap+nested+tex | 6.38 | 3.57 | 2.13 | 1.44 | 3.56 | 3.46 | 3.30 | 3.29 |
| cuda+heap+nested+tex+stackless | 5.78 | 3.19 | 1.83 | 1.21 | 1.11 | 1.10 | 1.11 | 1.13 |
A difficult situation, but, unlike the CPU version of the tree traversal, it is clear that each optimization step brings tangible results. The implementation of 'opencl + heap + cycle' is almost 6 times slower than an exact solution with full function calculation
| a) | b) |
| Fig. 11. Dependence of the function calculation time. | |
It can be seen that for small
Результаты запуска на GeForce GTX 1080 Ti (одинарная точность)
Таблица 7. Зависимость времени вычисления (в секундах) функции  от размера блока для различных GPU реализаций при количестве тел
от размера блока для различных GPU реализаций при количестве тел  и
и 
| Размер блока/ядро | 8 | 16 | 32 | 64 | 128 | 256 | 512 | 1024 |
|---|---|---|---|---|---|---|---|---|
| opencl+dense | 47.8 | 23.4 | 11.6 | 11.59 | 12.8 | 12.8 | 12.8 | 12.8 |
| cuda+dense | 49.0 | 23.8 | 11.9 | 11.8 | 11.7 | 11.7 | 11.7 | 11.7 |
| opencl+heap+cycle | 7.48 | 8.26 | 7.73 | 7.36 | 7.33 | 7.27 | 7.25 | 7.26 |
| opencl+heap+nested | 1.33 | 1.20 | 1.41 | 2.46 | 2.53 | 2.49 | 2.44 | 2.47 |
| cuda+heap+nested | 1.23 | 1.10 | 1.31 | 2.28 | 2.29 | 2.28 | 2.23 | 2.25 |
| cuda+heap+nested+tex | 0.88 | 0.68 | 0.654 | 1.6 | 1.6 | 1.6 | 1.6 | 1.6 |
| cuda+heap+nested+tex+stackless | 0.71 | 0.47 | 0.45 | 0.43 | 0.43 | 0.42 | 0.41 | 0.395 |
| Рис 12. Зависимость времени вычисления функции |
When using the GeForce GTX 1080 Ti for calculation, the difference between tree walks with a stack and without a stack is up to two times, provided that we neglect the time it takes to build the tree. This fact pushes us to ensure that in the future porting to the GPU and building a tree. A comparison of tables 5-7 shows that there is no single optimal block size for a different number of bodies, and even more so for different GPU architectures, moreover, the calculation time difference can reach several times, even if you do not take boundary values into account. Thus, before lengthy calculations, it makes sense to determine the optimal block size for each configuration.
The main thing that we have achieved is the ability to model pairwise interaction of a little over a million bodies (
Conclusion
The use of embedded methods for solving differential equations makes it possible to solve similar problems with a high level of accuracy at a relatively small time cost, and the application of algorithms for approximating the function of calculating the pairwise attraction forces allows us to process colossal volumes of interacting bodies. Thus, unlike the aliens from the “Three-body Tasks”, we are able to solve the problem
Visualization
For those who have read to the end, I will give a few more videos with visualization of the evolution of the systems of bodies.
Simulation of a collision of two galaxies. The total number of bodies is 60 thousand.
Modeling the evolution of a galaxy consisting of a million stars. In the center is a body with a mass of 99% of the total. Single particles are almost indistinguishable. Already more like a wave in a drop of liquid. Colorized according to speed module. Low speed - blue, medium - green, high - red. It is seen that in the center the speed is higher, and gradually decreases to the edges, and the lowest in the equatorial plane.
A more 'dynamic' simulation of the evolution of a million-star galaxy. In the center is a body with a mass of 10% of the total. The central body affects the rest significantly less. First, the “stars” fly apart, then gather back into several clusters, and at the end again form one large cluster.
In the process of modeling, about 5% of the “stars” left the initial region irrevocably.
At the 10th second, it very much resembles the existing cartwheel galaxy .
The project code can be found on the github .
