Neural networks and language philosophy
- Transfer
Why the theories of Wittgenstein remain the basis of the entire modern NLP
Vector representation of words - perhaps one of the most beautiful and romantic ideas in the history of artificial intelligence. The philosophy of language is a section of philosophy that explores the connection between language and reality and how to make speech meaningful and understandable. And the vector representation of words is a very specific method in modern natural language processing (Natural Language Processing, NLP). In a sense, it is an empirical proof of the theories of Ludwig Wittgenstein, one of the most relevant philosophers of the last century. For Wittgenstein, the use of words is a move in a social language game.played by community members who understand each other. The meaning of a word depends only on its usefulness in context; it does not relate one-to-one with an object from the real world.
Of course, to understand the exact meaning of the word is very difficult. There are many aspects to consider:
All these aspects, in the end, boil down to one thing: know how to use the word.
The concept of meaning and why an ordered set of characters has a certain connotation in the language is not only a philosophical question, but also probably the biggest problem that AI specialists working with NLP face. It is quite obvious to the Russian-speaking person that the “dog” is an “animal” and it looks more like a “cat” than a “dolphin”, but this task is far from simple for a systematic solution.
By slightly correcting Wittgenstein's theories, we can say that dogs are like cats, because they often appear in the same contexts: dogs and cats are more likely to be associated with the words “house” and “garden” than with the words “sea” and the "ocean". It is this intuition that underlies Word2Vec , one of the most famous and successful implementations of the vector representation of words. Today, machines are far from a true understanding of long texts and passages, but the vectorial representation of words is undoubtedly the only method that allowed us to make the biggest step in this direction over the past decade.
In many computer problems, the first problem is to present the data in numerical form; words and sentences are probably the hardest to imagine in this form. In our setting, D words are selected from the dictionary , and each word can be assigned a numeric index i .
For many decades, the classical approach has been adopted to represent each word as a numerical D-dimensional vector of all zeros, except for the one in position i. As an example, consider a dictionary of three words: "dog", "cat" and "dolphin" (D = 3). Each word can be represented as a three-dimensional vector: “dog” corresponds to [1,0,0], “cat” - [0,1,0], and “dolphin”, obviously, [0,0,1]. The document can be represented as a D-dimensional vector, where each element counts occurrences of the i-th word in the document. This model is called Bag-of-words (BoW), and it has been used for decades.
Despite its success in the 90s, BoW lacked the only interesting function of words: their meaning. We know that two very different words can have similar meanings, even if they are completely different from a spelling point of view. “Cat” and “dog” are both domestic animals, “king” and “queen” are close to each other, “apple” and “cigarette” are completely unrelated. We know this , but in the BoW model, all these words are at the same distance in the vector space: 1.
The same problem applies to documents: using BoW, one can conclude that documents are similar only if they contain the same word a certain number of times. And here comes Word2Vec, introducing many philosophical questions into machine learning terms that Wittgenstein talked about in his Philosophical Studies 60 years ago.
In a dictionary of size D, where a word is identified by its index, the goal is to calculate the N-dimensional vector representation of each word with N << D. Ideally, we want it to be a dense vector representing some semantically specific aspects of meaning. For example, we ideally want the “dog” and “cat” to have similar ideas, and the “apple” and “cigarette” are very distant in the vector space.
We want to perform some basic algebraic operations on vectors, such as
Word2Vec is not directly trained by this presentation, but receives it as a side effect of the classification without a teacher. The average NLP corpus dataset consists of a set of sentences; each word from the sentence appears in the context of the surrounding words. The purpose of the classifier is to predict the target word, taking context words as input. For the sentence “brown dog plays in the garden,” the words [brown, plays, in, garden] are provided as input data, and she must predict the word “dog”. This task is considered as learning without a teacher, since the corpus does not need to be marked with an external source of truth: with a set of sentences, you can always automatically create positive and negative examples. Considering the "brown dog playing in the garden" as a good example,
And now the application of Wittgenstein's theories is quite clear: the context is crucial for the vector representation of words, since in his theories it is important to attach meaning to the word. If two words have similar meanings, they will have similar representations (a small distance in N-dimensional space) only because they often appear in similar contexts. Thus, the "cat" and "dog" will eventually have close vectors, because they often appear in the same contexts: it is useful for the model to use similar vector representations for them, because this is the most convenient thing that it can do, to get better results in predicting two words based on their contexts.
The original article suggests two different architectures: CBOW and Skip-gram. In both cases, verbal representations are trained along with the specific classification task, providing the best possible vector representations of words that maximize model performance.

Figure 1. Comparison of CBOW and Skip-gram
CBOW architecturesmeans Continuous Bag of Words, and its task is to guess the word taking into account the context as input. Inputs and outputs are represented as D-dimensional vectors, which are projected in N-dimensional space with common weights. We are only looking for weights to project. In essence, the vector representation of words is a D × N matrix, where each row represents a dictionary word. All context words are projected into one position, and their vector representations are averaged; therefore, word order does not affect the result.
Skip-gram does the same thing, but vice versa: trying to predict context words Cby taking as input the target word. The task of predicting several context words can be reformulated into a set of independent binary classification problems, and now the goal is to predict the presence (or absence) of context words.
As a rule, Skip-gram takes more time to learn and often gives slightly better results, but, as usual, different applications have different requirements and it is difficult to predict in advance which of them will show the best result. Despite the simplicity of the concept, learning architectures of this kind is a real nightmare due to the amount of data and processing power required to optimize the scales. Fortunately, on the Internet, you can find some pre-trained vector representations of words, and you can study vector space — the most interesting — with just a few lines of Python code.
Above the classic Word2Vec in recent years, many possible improvements have been proposed. The two most interesting and frequently used ones are GloVe (Stanford University) and fastText (developed by Facebook). They are trying to identify and overcome the limitations of the original algorithm.
In the original scientific article, the authors of GloVe emphasize that the training model in a separate local context makes poor use of global statistics of the corpus. The first step to overcome this limitation is to create a global matrix X , where each element i, j counts the number of references to the word j in the context of the word i. The second important idea of this document is the understanding that only probabilities are not enough to reliably predict values, but a co-occurrence matrix is also required, from where you can directly extract certain aspects of values.
This probability ratio becomes the starting point for studying the vector representation of words. We want to be able to calculate vectors that, in combination with a specific function F, keep this relation constant in the space of a vector representation.

Figure 2. The most general formula for the vector representation of words in the GloVe model
The function F and the dependence on the word k can be simplified by replacing the exponentials and fixed offsets, which results in the minimization function of errors using the least squares method J :
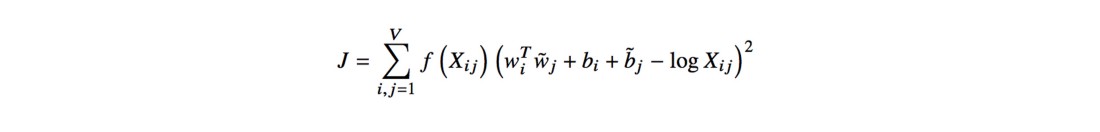
Figure 3. The final function to calculate the vector representation of words in the GloVe model.
The f function is a counting function that tries not to make very frequent and rare matches, while bi and bj are offsets to restore the symmetry of the function. In the last paragraphs of the article, it is shown that learning this model is not much different from learning the classic Skip-gram model, although in the empirical tests GloVe surpasses both Word2Vec implementations. FastText
, on the other handcorrects a completely different flaw in Word2Vec: if the model is taught to directly encode a single D-dimensional vector, then the internal structure of the words is ignored. Instead of directly encoding the encoding of words that study verbal representations, fastText suggests studying the N-grams of characters and representing words as the sum of the N-gram vectors. For example, when N = 3, the word “flower” is encoded as 6 different 3-grams [<fl, flo, low, Debt, wer, er>] plus a special sequence <flower>. Notice how the angle brackets are used to mark the beginning and end of the word. Thus, a word is represented by its index in a word dictionary and a set of N-grams, which it contains, mapped to integers using the hashing function.
As we already said, to use these vector views you need only a few lines of Python code. I conducted several experiments with the 50-dimensional GloVe model , trained on 6 billion words from Wikipedia's sentences, and also with the 300-dimensional fastText model, trained on Common Crawl (which gave 600 billion tokens). This paragraph contains references to the results of both experiments only to prove the concepts and give a general understanding of the topic.
First of all, I wanted to check out some basic similarities of words, the simplest, but important feature of their vector representation. As expected, the most similar words with the word "dog" were "cat" (0.92), "dogs" (0.85), "horse" (0.79), "puppy" (0.78) and "pet" (0.77). Note that the plural form has almost the same meaning as the singular. Again, for us it is rather trivial to say so, but for a car it is not at all a fact. Now food: the most similar words for "pizza" are "sandwich" (0.87), "sandwiches" (0.86), "snack" (0.81), "pastries" (0.79), "fries" (0.79) and "burgers" ( 0.78). It makes sense, the results are satisfactory, and the model behaves quite well.
The next step is to perform some basic calculations in the vector space and check how well the model has learned some important properties. Indeed, as a result of the calculation of vectors
And now the fun part. Following the same idea, we will try to add and subtract concepts. For example, What is the American equivalent of pizza for Italians?

Figure 4. To all Dutch readers: accept it as a compliment, okay?
To use these pre-trained vector representations, good practical resources can be found here andhere . Gensim is a simple and complete Python library with some ready-to-use algebraic and similarity functions. These pre-trained vector representations can be used in various (and useful) ways, for example, to improve the performance of mood analyzers or language models. Whatever the task, the use of N-dimensional vectors will significantly improve the efficiency of the model compared to direct encoding. Of course, training on vector representations in a specific area will further improve the result, but this may require, perhaps, excessive efforts and time.
Vector representation of words - perhaps one of the most beautiful and romantic ideas in the history of artificial intelligence. The philosophy of language is a section of philosophy that explores the connection between language and reality and how to make speech meaningful and understandable. And the vector representation of words is a very specific method in modern natural language processing (Natural Language Processing, NLP). In a sense, it is an empirical proof of the theories of Ludwig Wittgenstein, one of the most relevant philosophers of the last century. For Wittgenstein, the use of words is a move in a social language game.played by community members who understand each other. The meaning of a word depends only on its usefulness in context; it does not relate one-to-one with an object from the real world.
For a large class of cases in which we use the word "value", it can be defined as the meaning of a word is its use in language .
Of course, to understand the exact meaning of the word is very difficult. There are many aspects to consider:
- to which object the word may belong;
- what is the part of speech;
- is it an idiomatic expression;
- all shades of meanings;
- and so on.
All these aspects, in the end, boil down to one thing: know how to use the word.
The concept of meaning and why an ordered set of characters has a certain connotation in the language is not only a philosophical question, but also probably the biggest problem that AI specialists working with NLP face. It is quite obvious to the Russian-speaking person that the “dog” is an “animal” and it looks more like a “cat” than a “dolphin”, but this task is far from simple for a systematic solution.
By slightly correcting Wittgenstein's theories, we can say that dogs are like cats, because they often appear in the same contexts: dogs and cats are more likely to be associated with the words “house” and “garden” than with the words “sea” and the "ocean". It is this intuition that underlies Word2Vec , one of the most famous and successful implementations of the vector representation of words. Today, machines are far from a true understanding of long texts and passages, but the vectorial representation of words is undoubtedly the only method that allowed us to make the biggest step in this direction over the past decade.
From BoW to Word2Vec
In many computer problems, the first problem is to present the data in numerical form; words and sentences are probably the hardest to imagine in this form. In our setting, D words are selected from the dictionary , and each word can be assigned a numeric index i .
For many decades, the classical approach has been adopted to represent each word as a numerical D-dimensional vector of all zeros, except for the one in position i. As an example, consider a dictionary of three words: "dog", "cat" and "dolphin" (D = 3). Each word can be represented as a three-dimensional vector: “dog” corresponds to [1,0,0], “cat” - [0,1,0], and “dolphin”, obviously, [0,0,1]. The document can be represented as a D-dimensional vector, where each element counts occurrences of the i-th word in the document. This model is called Bag-of-words (BoW), and it has been used for decades.
Despite its success in the 90s, BoW lacked the only interesting function of words: their meaning. We know that two very different words can have similar meanings, even if they are completely different from a spelling point of view. “Cat” and “dog” are both domestic animals, “king” and “queen” are close to each other, “apple” and “cigarette” are completely unrelated. We know this , but in the BoW model, all these words are at the same distance in the vector space: 1.
The same problem applies to documents: using BoW, one can conclude that documents are similar only if they contain the same word a certain number of times. And here comes Word2Vec, introducing many philosophical questions into machine learning terms that Wittgenstein talked about in his Philosophical Studies 60 years ago.
In a dictionary of size D, where a word is identified by its index, the goal is to calculate the N-dimensional vector representation of each word with N << D. Ideally, we want it to be a dense vector representing some semantically specific aspects of meaning. For example, we ideally want the “dog” and “cat” to have similar ideas, and the “apple” and “cigarette” are very distant in the vector space.
We want to perform some basic algebraic operations on vectors, such as
король+женщина−мужчина=королева. It would be desirable that the distance between the vectors "actor" and "actress" would largely coincide with the distance between the "prince" and "princess". Despite the fact that these results are quite utopian, experiments show that Word2Vec vectors exhibit properties that are very close to these.Word2Vec is not directly trained by this presentation, but receives it as a side effect of the classification without a teacher. The average NLP corpus dataset consists of a set of sentences; each word from the sentence appears in the context of the surrounding words. The purpose of the classifier is to predict the target word, taking context words as input. For the sentence “brown dog plays in the garden,” the words [brown, plays, in, garden] are provided as input data, and she must predict the word “dog”. This task is considered as learning without a teacher, since the corpus does not need to be marked with an external source of truth: with a set of sentences, you can always automatically create positive and negative examples. Considering the "brown dog playing in the garden" as a good example,
And now the application of Wittgenstein's theories is quite clear: the context is crucial for the vector representation of words, since in his theories it is important to attach meaning to the word. If two words have similar meanings, they will have similar representations (a small distance in N-dimensional space) only because they often appear in similar contexts. Thus, the "cat" and "dog" will eventually have close vectors, because they often appear in the same contexts: it is useful for the model to use similar vector representations for them, because this is the most convenient thing that it can do, to get better results in predicting two words based on their contexts.
The original article suggests two different architectures: CBOW and Skip-gram. In both cases, verbal representations are trained along with the specific classification task, providing the best possible vector representations of words that maximize model performance.

Figure 1. Comparison of CBOW and Skip-gram
CBOW architecturesmeans Continuous Bag of Words, and its task is to guess the word taking into account the context as input. Inputs and outputs are represented as D-dimensional vectors, which are projected in N-dimensional space with common weights. We are only looking for weights to project. In essence, the vector representation of words is a D × N matrix, where each row represents a dictionary word. All context words are projected into one position, and their vector representations are averaged; therefore, word order does not affect the result.
Skip-gram does the same thing, but vice versa: trying to predict context words Cby taking as input the target word. The task of predicting several context words can be reformulated into a set of independent binary classification problems, and now the goal is to predict the presence (or absence) of context words.
As a rule, Skip-gram takes more time to learn and often gives slightly better results, but, as usual, different applications have different requirements and it is difficult to predict in advance which of them will show the best result. Despite the simplicity of the concept, learning architectures of this kind is a real nightmare due to the amount of data and processing power required to optimize the scales. Fortunately, on the Internet, you can find some pre-trained vector representations of words, and you can study vector space — the most interesting — with just a few lines of Python code.
Possible improvements: GloVe and fastText
Above the classic Word2Vec in recent years, many possible improvements have been proposed. The two most interesting and frequently used ones are GloVe (Stanford University) and fastText (developed by Facebook). They are trying to identify and overcome the limitations of the original algorithm.
In the original scientific article, the authors of GloVe emphasize that the training model in a separate local context makes poor use of global statistics of the corpus. The first step to overcome this limitation is to create a global matrix X , where each element i, j counts the number of references to the word j in the context of the word i. The second important idea of this document is the understanding that only probabilities are not enough to reliably predict values, but a co-occurrence matrix is also required, from where you can directly extract certain aspects of values.
Consider two words i and j, which are of particular interest. For concreteness, we assume that we are interested in the concept of a thermodynamic state for which we can takei = лёдandj = пар. The connection of these words can be investigated by studying the ratio of their probabilities of joint occurrence with the help of different probing words, k. For words k associated with ice, but not steam, sayk = тело[solid body, state of matter], we expect the ratio Pik / Pjk to be greater. Similarly, for words k related to steam, but not to ice, let's say thek = газratio should be small. For words like “water” or “fashion,” which are either equally related to ice and steam, or are not related to them, this relationship should be close to one.
This probability ratio becomes the starting point for studying the vector representation of words. We want to be able to calculate vectors that, in combination with a specific function F, keep this relation constant in the space of a vector representation.

Figure 2. The most general formula for the vector representation of words in the GloVe model
The function F and the dependence on the word k can be simplified by replacing the exponentials and fixed offsets, which results in the minimization function of errors using the least squares method J :
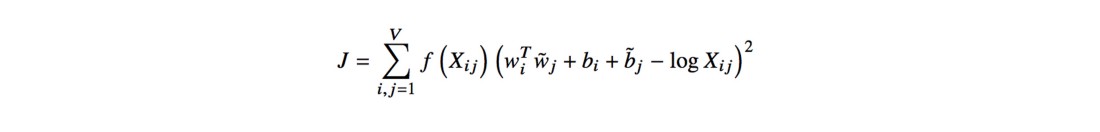
Figure 3. The final function to calculate the vector representation of words in the GloVe model.
The f function is a counting function that tries not to make very frequent and rare matches, while bi and bj are offsets to restore the symmetry of the function. In the last paragraphs of the article, it is shown that learning this model is not much different from learning the classic Skip-gram model, although in the empirical tests GloVe surpasses both Word2Vec implementations. FastText
, on the other handcorrects a completely different flaw in Word2Vec: if the model is taught to directly encode a single D-dimensional vector, then the internal structure of the words is ignored. Instead of directly encoding the encoding of words that study verbal representations, fastText suggests studying the N-grams of characters and representing words as the sum of the N-gram vectors. For example, when N = 3, the word “flower” is encoded as 6 different 3-grams [<fl, flo, low, Debt, wer, er>] plus a special sequence <flower>. Notice how the angle brackets are used to mark the beginning and end of the word. Thus, a word is represented by its index in a word dictionary and a set of N-grams, which it contains, mapped to integers using the hashing function.
Experiments and possible applications
As we already said, to use these vector views you need only a few lines of Python code. I conducted several experiments with the 50-dimensional GloVe model , trained on 6 billion words from Wikipedia's sentences, and also with the 300-dimensional fastText model, trained on Common Crawl (which gave 600 billion tokens). This paragraph contains references to the results of both experiments only to prove the concepts and give a general understanding of the topic.
First of all, I wanted to check out some basic similarities of words, the simplest, but important feature of their vector representation. As expected, the most similar words with the word "dog" were "cat" (0.92), "dogs" (0.85), "horse" (0.79), "puppy" (0.78) and "pet" (0.77). Note that the plural form has almost the same meaning as the singular. Again, for us it is rather trivial to say so, but for a car it is not at all a fact. Now food: the most similar words for "pizza" are "sandwich" (0.87), "sandwiches" (0.86), "snack" (0.81), "pastries" (0.79), "fries" (0.79) and "burgers" ( 0.78). It makes sense, the results are satisfactory, and the model behaves quite well.
The next step is to perform some basic calculations in the vector space and check how well the model has learned some important properties. Indeed, as a result of the calculation of vectors
женщина+актер-мужчина, the result is the “actress” (0.94), and as a result of the calculation мужчина+королева-женщина , the word “king” (0.86). Generally speaking, if the value is a:b=c:d, the word d should be received as d=b-a+c. Moving on to the next level, it’s impossible to imagine how these vector operations even describe geographic aspects: we know that Rome is the capital of Italy, since Berlin is the capital of Germany, in fact Берлин+Италия-Рим=Германия (0.88), as well Лондон+Германия-Англия=Берлин (0.83).And now the fun part. Following the same idea, we will try to add and subtract concepts. For example, What is the American equivalent of pizza for Italians?
пицца+Америка-Италия=бургеры (0.60)then чизбургеры (0.59). Since I moved to Holland, I always say that this country is a mixture of three things: some American capitalism, Swedish cold and quality of life, and finally a pinch of Neapolitan abundance . By slightly changing the original theorem, removing a bit of Swiss accuracy, we get Holland (0.68) as a result США+Швеция+Неаполь-Швейцария: quite impressive, to be honest. 
Figure 4. To all Dutch readers: accept it as a compliment, okay?
To use these pre-trained vector representations, good practical resources can be found here andhere . Gensim is a simple and complete Python library with some ready-to-use algebraic and similarity functions. These pre-trained vector representations can be used in various (and useful) ways, for example, to improve the performance of mood analyzers or language models. Whatever the task, the use of N-dimensional vectors will significantly improve the efficiency of the model compared to direct encoding. Of course, training on vector representations in a specific area will further improve the result, but this may require, perhaps, excessive efforts and time.
