A closed universe - how it turns out, how to explain it more simply, and why it is impossible to get out of it

Introduction

A lot of popular articles about cosmology, where they write about dark matter, the early stages of the Universe, etc., have been written. However, many people do not understand at all what a closed Universe is, such as ours, and why it is fundamentally impossible to get out of it. This requires a certain minimum of knowledge from the general theory of relativity. This article is written to clarify these things to those interested, without resorting to the apparatus of the general theory of relativity (if possible). Nevertheless, a good knowledge of the school course in physics and a certain minimum from the special theory of relativity (STR) are assumed. We will begin to consider the issue from the point of view of the Newtonian theory of universal gravitation.

1. How a closed world is formed.

Consider a homogeneous ball consisting of matter, particles of which interact only according to the law of universal gravitation. Such matter is also called pulverized. Of course, such a ball cannot be at rest due to gravitational forces. Suppose that at the initial stage, matter expands uniformly in all directions with speed 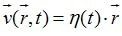. Here is the radius vector of the particle of matter in the ball, is the speed of this particle at time t, is the function of time that will have to be determined from the equations of mechanics. It is easy to see that such a velocity distribution is indeed a solution. Let the total particle mass of the ball be M , and let the outer radius be R (t).Since the particle is attracted only by matter that is closer to the center of the ball (the force of attraction of the outer sphere inside it is zero - this is a well-known task from the school course), the acceleration of universal gravitation at a point is equal to the gravitational constant. The kinematic acceleration of a particle is equal
.
From here it 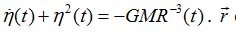shrinks and disappears from the equations. A dot over a function means time differentiation. For R (t) we have the equation. We get a joint system of ordinary differential equations, such a distribution of speeds is really a solution. There is no need to look for a solution to the resulting system of equations; it is only important that it exists. It is easy to see that in this case the ball remains homogeneous all the time. All particles of matter move away from each other at a speed proportional to the distance between them (the Hubble law of the recession of galaxies is the Hubble constant).
If the initial expansion rate is not too high and the total mechanical energy is negative, then at some point the expansion will be replaced by compression. At this moment, the velocity and kinetic energy of all particles are equal to zero. Let the radius of the ball at this moment . Under mass Mrefers to the sum of the masses of the particles of the ball taken separately - gravitational interaction reduces the weight of the ball according to the special theory of relativity, it is less than M . Denote the density of the ball at the moment the expansion stops. The energy of the gravitational interaction of the particles of the ball can be easily calculated by simple integration. It is equal.

This energy according to SRT reduces the rest mass of the ball to a value . Here c is the speed of light. Since the full energy of the ball is conserved, this will be true at any given time. This shows that at a constant density, an increasewill cause the expression in brackets to go to zero or even become negative. What does turning the mass to zero mean for a body at rest (meaning the center of mass)? Such a body ceases to be observable. It does not interact gravitationally, in collisions it is impossible to detect. The ball falls out of our world. Collapse into a black hole has nothing to do with this phenomenon - a black hole necessarily has an outside mass observed.
Exact calculation using the general theory of relativity shows another interesting thing. As the amount of matter in the ball increases, that is, M , the circumference of the ball first grows, and then begins to fall. Gravity changes the geometry of space, as a result, the size of the ball vanishes along with its mass - for an external observer.

2. What does the isolation of the world mean?

The resulting closed world is impossible to leave. Indeed, suppose that something with non-zero mass-energy got out of the ball into the outside world. For the external observer, this means the appearance of mass-energy from nothing - for him, the mass of the closed world is zero, and this world itself is unobservable. To get from outside into this closed world is also impossible - you have to crawl into the neck of a zero size. Actually, it will be impossible to find this throat of zero size. For a two-dimensional world, the situation looks like this.

For a two-dimensional object of nonzero size, it is impossible to get from a plane to a sphere. It will not work to crawl through the neck - the point of contact of the sphere with the plane.

Conclusion

Here, the details regarding the internal structure of the closed world were not addressed, since much would have to be involved from the general theory of relativity (GR). It would be necessary to explain how geometry is determined in GR, as a result of which the closed world turns out to be a three-dimensional sphere - the surface of a four-dimensional ball. All points of such a sphere are absolutely equal, all observers at these points see the same picture. This is the simplest case in cosmology - in reality, our Universe is not so symmetrical, and at the initial or final stages it is not at all symmetrical.
The reader may ask, how can a huge amount of matter in the form of such a uniform sphere disappear from the material world? This matter actually turns into energy, which remains in the outside world. In fact, we, living in a closed world, have no decisive arguments in favor of the fact that, in addition to our world containing a finite amount of matter, there are some other worlds. A closed world has a finite lifetime - from the beginning of expansion or the Big Bang to compression to a point. Will there be anything left after this, one can only speculate from philosophical considerations.