Gravity is not fashionable
There are a lot of popular science articles and books about gravity, which talk about the curvature of space-time and provide pictures with a pressed sheet (trampoline, mat). Let's break this order of things together! Under the cut you will find yourself quite a standard but not fashionable description of gravity.
Emperor Sarlac Grant Scenticus III was very fond of geometry. And his love was so strong that one day he decided on sacrilege - to test it experimentally. This was an unheard-of thing: is it a joke, how can geometry, the perfect brainchild of pure logic, get dirty with some mundane experiments? The great geometer Haffleath himself came to see this.
In the early morning, Grant sent the two best gliders in different directions, strictly telling them to fly exactly one hundred kilometers (in fact, the distance was equal to one hundred and thirty skeletons, but this is almost no different from one hundred kilometers) without turning anywhere, strictly in a straight line, merging paint from tanks attached to gliders along the way.
As you probably already understood, in this way he wanted to verify the theorem on the sum of the angles of a triangle. The point of departure of the two gliders and their destinations were to become the vertices of this triangle.
Without dragging out the story, we immediately turn to the climax: the sum of the angles was more than 180 degrees.
***
There should be a highly artistic and long description of the general shock.
***
Halfclit was so shocked by the outcome of the experiment that he decided to look at the grief-triangle with his own eyes and passed accelerated flight courses on the glider. Let’s look at a picture of what he saw, kindly provided to us by a satellite of observation, launched into the orbit of Sarlak by the Ptaagh civilization, whose ideas about what the satellite image should be are somewhat different from ours.
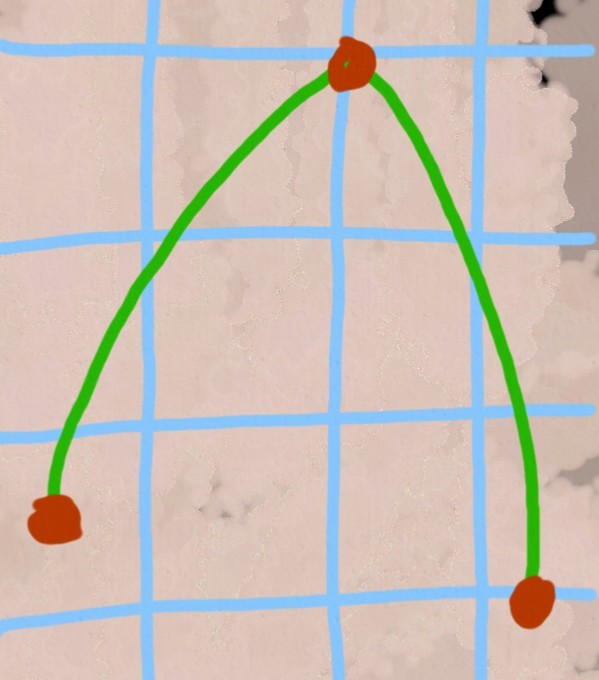
“Damn flyers!” Exclaimed Hafclit, “they couldn’t even stand the course!” However, at a meeting convened in Grant’s Palace on the occasion of the opening of Hefclit, the “damn flyers” stated that they had not strayed from the course, and even showed tapes scribbled with instruments, which made it clear that they did not turn. And then the philosopher Niu-Tan gave a voice.
“Obviously,” he said, “that both flyers and geometry are all right.” I assume that the flight lines were curved due to the fact that some unknown force was acting on the gliders, pulling them to the center of the triangle.
Thus, the honor of geometry was saved and a new strength was found. And in Grant's mind, many ideas of new experiments were born.
Perhaps this is where we could finish the story. But, let's look at one more of the images of the Ptaagh satellite:
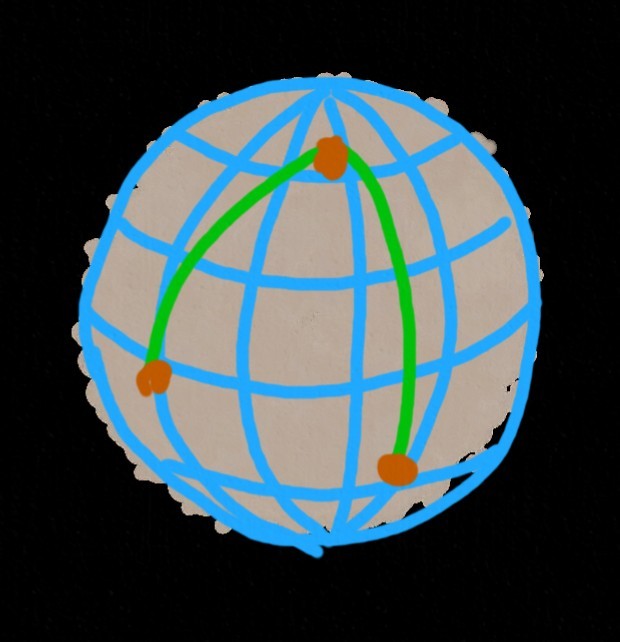
See? Do you see it? Yes, you guessed it, none of the inhabitants of Sarlak knew that they live on the surface of the ball (and, quite small). And the curvature of the lines was explained only by the fact that the surface itself on which they were drawn was a curve. However, if you do not know about curvature, then the best possible explanation (with the exception of optical illusions and the inexperience of flyers) is the presence of a certain force that bends the trajectories of gliders (and everything else). Note that this force will affect all bodies. Moreover, it will act equally on all these bodies .
Well, we have one such power in sight. It acts on everything, it is impossible to hide from it, and its effect on all bodies (namely, the acceleration given by it to bodies) is the same. As the title of the publication intrusively tells us, it is, of course, gravity. Fortunately, we realized in time that gravity is just a manifestation of the fact that space is curved. Albert Einstein, a modest employee of the patent office in Switzerland and one of the greatest scientists of mankind, helped us to realize this (undoubtedly, the young and talented philosopher Han-Shten will also explain the power invented by Niu-Tan through curvature sometime on Sarlak).
Let's visually see this curvature on the example of pebbles flying near a dwarf planet (thanks Ptaagh):

Ptaagh helpfully noted the initial positions of the stones and drew their routes. Twisted. In addition to the average, which is direct. Something is wrong.
The wise Albert also understood that space and time are inseparable. There is only one single space-time. And not only space is curved, but also time. “But!” You say, reader, “how can time be crooked?” We will not delve into the wilds and say only one thing. The curvature of time is observed by us as acceleration . Over equal intervals of time, our stones will travel more and more distance. We turn once again to the satellite Ptaagh:

Here the routes are not depicted continuously, but in the form of separate segments, the flight of each of which takes the same time. Albert is right!
However, we are aware of another case where bodies move relative to us with the same acceleration. This happens if we ourselves move fast. From our point of view, everything around will move with the same acceleration (thereby, with which we move, but directed in the opposite direction). This similarity was noted by Einstein and named the principle of equivalence . How to distinguish the real curvature of space-time from the apparent one caused by our accelerated motion?
Ptaagh placed four stones in the vertices of a rhombus near the surface of the planet, released them and took two pictures in one frame at different points in time (stroboscopy):

The rhombus extended in the direction of the "gravitational force" and contracted in the transverse. This is due to the fact that the accelerations are directed not parallel to each other, but towards the center of the planet. And the acceleration increases as we approach the planet. As a result of this, the bodies that are closer to the planet move faster, and the bodies on the sides converge to the middle.
Such an effect, stretching the body in the direction of gravity and compressing in the transverse, is called tidal forces . It is tidal forces that are the real manifestation of gravity.
For a mathematically savvy reader: the metric of an observer resting in a gravitational field locally coincides with the metric of an observer moving with a properly selected acceleration. The first derivative of the metric also coincides. But the second derivative is already different, and it is it that is the mathematical "image" of tidal forces
When the gravity of a body or system of bodies changes rapidly (as, for example, when two black holes rotate around a common center), the “picture” of the curvature of space-time does not have time to smooth out when a new one is already formed. In space-time there is a “ripple”. This ripple we call gravitational waves. The influence of gravitational waves manifests itself in the form of periodic tension and compression of space-time in two mutually transverse directions, that is, in the form of tidal forces. At the same time, two different polarizations of gravitational waves are separated: (+) and (×).
This is how (+) - polarized


HSs appear: And so - (×) -polarized: The


blue grid here represents space.
Now let's think: can we somehow “feel” these waves? The answer is yes, we can.
Imagine an iron ball. When the space in which it is located begins to shrink and stretch, the atoms of which it consists begin to converge in one direction and move away in the other. However, the forces between them prevent them from moving as freely as they should. As a result of this, the deformation of the ball lags somewhat behind the deformation of space-time. Regarding space-time, the ball begins to vibrate, contracting and stretching. And such vibrations can let us know that right now GW pass through the ball. Unfortunately, the deformations are very small: the relative change in size under the influence of the GW recorded in September 2015 is ten to minus twenty-first degrees. I will write out this number:
0.000000000000000000001
If the ball were 3 times smaller than the Earth, a change in its size would be equal to the diameter of one proton. Therefore, the idea of one-piece HS detectors is somewhat unsuccessful.
Now instead of solid balls, hollow "letters G" are used, with laser beams running inside them. This is how the famous LIGO works. Changes in the dimensions of the "sleeves" of the detector manifest themselves in the form of changes in the phases of the laser beams, which can be determined as a result of the addition of two beams. In more detail about this, I may write someday later. And for those who can’t wait, I recommend this article by Shkaff , which, among other things, describes in detail how LIGO works.
Emperor Sarlac Grant Scenticus III was very fond of geometry. And his love was so strong that one day he decided on sacrilege - to test it experimentally. This was an unheard-of thing: is it a joke, how can geometry, the perfect brainchild of pure logic, get dirty with some mundane experiments? The great geometer Haffleath himself came to see this.
In the early morning, Grant sent the two best gliders in different directions, strictly telling them to fly exactly one hundred kilometers (in fact, the distance was equal to one hundred and thirty skeletons, but this is almost no different from one hundred kilometers) without turning anywhere, strictly in a straight line, merging paint from tanks attached to gliders along the way.
As you probably already understood, in this way he wanted to verify the theorem on the sum of the angles of a triangle. The point of departure of the two gliders and their destinations were to become the vertices of this triangle.
Without dragging out the story, we immediately turn to the climax: the sum of the angles was more than 180 degrees.
***
There should be a highly artistic and long description of the general shock.
***
Halfclit was so shocked by the outcome of the experiment that he decided to look at the grief-triangle with his own eyes and passed accelerated flight courses on the glider. Let’s look at a picture of what he saw, kindly provided to us by a satellite of observation, launched into the orbit of Sarlak by the Ptaagh civilization, whose ideas about what the satellite image should be are somewhat different from ours.

“Damn flyers!” Exclaimed Hafclit, “they couldn’t even stand the course!” However, at a meeting convened in Grant’s Palace on the occasion of the opening of Hefclit, the “damn flyers” stated that they had not strayed from the course, and even showed tapes scribbled with instruments, which made it clear that they did not turn. And then the philosopher Niu-Tan gave a voice.
“Obviously,” he said, “that both flyers and geometry are all right.” I assume that the flight lines were curved due to the fact that some unknown force was acting on the gliders, pulling them to the center of the triangle.
Thus, the honor of geometry was saved and a new strength was found. And in Grant's mind, many ideas of new experiments were born.
Perhaps this is where we could finish the story. But, let's look at one more of the images of the Ptaagh satellite:

See? Do you see it? Yes, you guessed it, none of the inhabitants of Sarlak knew that they live on the surface of the ball (and, quite small). And the curvature of the lines was explained only by the fact that the surface itself on which they were drawn was a curve. However, if you do not know about curvature, then the best possible explanation (with the exception of optical illusions and the inexperience of flyers) is the presence of a certain force that bends the trajectories of gliders (and everything else). Note that this force will affect all bodies. Moreover, it will act equally on all these bodies .
Well, we have one such power in sight. It acts on everything, it is impossible to hide from it, and its effect on all bodies (namely, the acceleration given by it to bodies) is the same. As the title of the publication intrusively tells us, it is, of course, gravity. Fortunately, we realized in time that gravity is just a manifestation of the fact that space is curved. Albert Einstein, a modest employee of the patent office in Switzerland and one of the greatest scientists of mankind, helped us to realize this (undoubtedly, the young and talented philosopher Han-Shten will also explain the power invented by Niu-Tan through curvature sometime on Sarlak).
Let's visually see this curvature on the example of pebbles flying near a dwarf planet (thanks Ptaagh):

Ptaagh helpfully noted the initial positions of the stones and drew their routes. Twisted. In addition to the average, which is direct. Something is wrong.
The wise Albert also understood that space and time are inseparable. There is only one single space-time. And not only space is curved, but also time. “But!” You say, reader, “how can time be crooked?” We will not delve into the wilds and say only one thing. The curvature of time is observed by us as acceleration . Over equal intervals of time, our stones will travel more and more distance. We turn once again to the satellite Ptaagh:

Here the routes are not depicted continuously, but in the form of separate segments, the flight of each of which takes the same time. Albert is right!
However, we are aware of another case where bodies move relative to us with the same acceleration. This happens if we ourselves move fast. From our point of view, everything around will move with the same acceleration (thereby, with which we move, but directed in the opposite direction). This similarity was noted by Einstein and named the principle of equivalence . How to distinguish the real curvature of space-time from the apparent one caused by our accelerated motion?
Ptaagh placed four stones in the vertices of a rhombus near the surface of the planet, released them and took two pictures in one frame at different points in time (stroboscopy):

The rhombus extended in the direction of the "gravitational force" and contracted in the transverse. This is due to the fact that the accelerations are directed not parallel to each other, but towards the center of the planet. And the acceleration increases as we approach the planet. As a result of this, the bodies that are closer to the planet move faster, and the bodies on the sides converge to the middle.
Such an effect, stretching the body in the direction of gravity and compressing in the transverse, is called tidal forces . It is tidal forces that are the real manifestation of gravity.
For a mathematically savvy reader: the metric of an observer resting in a gravitational field locally coincides with the metric of an observer moving with a properly selected acceleration. The first derivative of the metric also coincides. But the second derivative is already different, and it is it that is the mathematical "image" of tidal forces
When the gravity of a body or system of bodies changes rapidly (as, for example, when two black holes rotate around a common center), the “picture” of the curvature of space-time does not have time to smooth out when a new one is already formed. In space-time there is a “ripple”. This ripple we call gravitational waves. The influence of gravitational waves manifests itself in the form of periodic tension and compression of space-time in two mutually transverse directions, that is, in the form of tidal forces. At the same time, two different polarizations of gravitational waves are separated: (+) and (×).
This is how (+) - polarized


HSs appear: And so - (×) -polarized: The


blue grid here represents space.
Now let's think: can we somehow “feel” these waves? The answer is yes, we can.
Imagine an iron ball. When the space in which it is located begins to shrink and stretch, the atoms of which it consists begin to converge in one direction and move away in the other. However, the forces between them prevent them from moving as freely as they should. As a result of this, the deformation of the ball lags somewhat behind the deformation of space-time. Regarding space-time, the ball begins to vibrate, contracting and stretching. And such vibrations can let us know that right now GW pass through the ball. Unfortunately, the deformations are very small: the relative change in size under the influence of the GW recorded in September 2015 is ten to minus twenty-first degrees. I will write out this number:
0.000000000000000000001
If the ball were 3 times smaller than the Earth, a change in its size would be equal to the diameter of one proton. Therefore, the idea of one-piece HS detectors is somewhat unsuccessful.
Now instead of solid balls, hollow "letters G" are used, with laser beams running inside them. This is how the famous LIGO works. Changes in the dimensions of the "sleeves" of the detector manifest themselves in the form of changes in the phases of the laser beams, which can be determined as a result of the addition of two beams. In more detail about this, I may write someday later. And for those who can’t wait, I recommend this article by Shkaff , which, among other things, describes in detail how LIGO works.
