Ask Ethan No. 13: Where did the matter come from?

When you see your copy of antimatter that runs toward you, think carefully before hugging her.
- J. Richard Gott III

Perhaps you did not think about the fact that the whole Earth and everything that is on it was created from matter. It seems intuitive and cannot be otherwise. However, the laws of nature have not yet told us why the universe is so arranged.

The reader asks:

Is it true that at the dawn of the Universe, matter and antimatter were created in equal quantities? And if not, is it known why such an inequality arose?
And if their number was the same, why is antimatter so small? Is there a mechanism for explaining the prevalence of matter over antimatter in the visible part of the universe?

Think about it.



This is part of the universe. Hundreds of billions of stars and star systems exist only in our galaxy. Hundreds of billions of galaxies are in the visible part of the universe. Of all of them, we studied only our own star system, which, not surprisingly, turned out to be created from matter, not antimatter.



But, apparently, the rest of the Universe is also made of matter. More precisely, the material in the Universe is full, and if there was somewhere a part made of antimatter, we would witness a tremendous catastrophe when matter and antimatter meet.



For example, the space between stars in galaxies is full of material, even if there are no stars. The cosmos is vast and the density of matter is low. It can be calculated - if we threw one particle of antimatter (say, an antiproton) in space, how long would it have lived before meeting with a particle from matter and annihilation. On average, it would last 300 years in the interstellar space of our galaxy - which is nothing compared to the age of the galaxy. This limitation indicates that among the matter there can be particles of antimatter only in an amount of the order of 1 particle per 10 ¹⁵ .



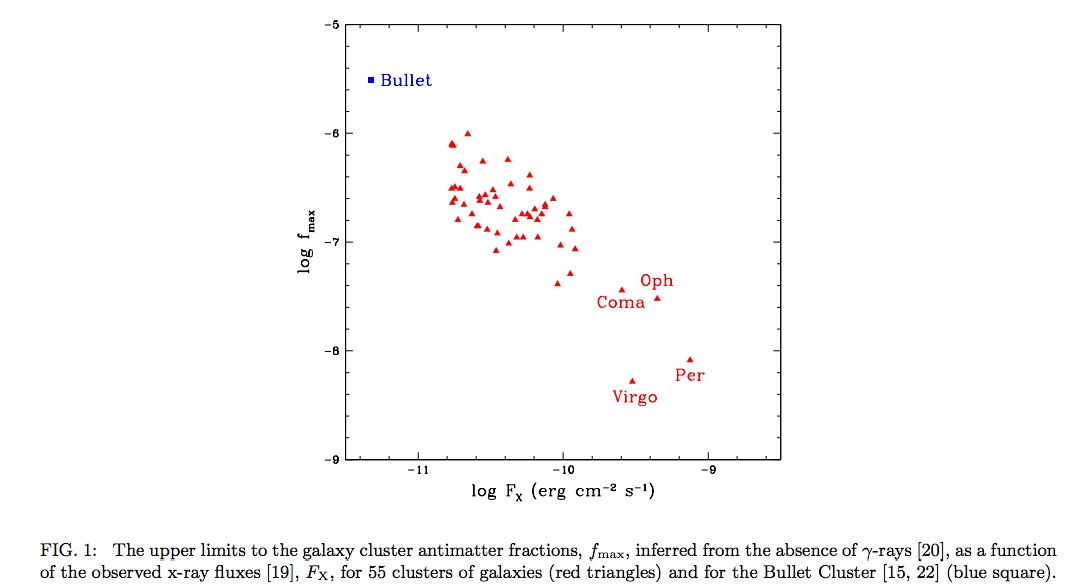
On a larger scale, we mapped galaxies and their clusters, looked around at different wavelengths, including visible light, infrared waves, microwaves, radio, ultraviolet, x-rays and gamma rays. Specifically, x-rays and gamma rays are very important for observations, because when annihilating matter and antimatter, they emit characteristic high-energy radiation, which we can detect.



Having studied 55 galactic clusters, at distances from several million light years to three billion, we saw that on the cosmic scales 99.999% + of all matter is ordinary matter, not antimatter.



And yet this is unexpected. You may have heard something about the formula E = mc ², and you know that she claims that not only energy is contained in the mass, but that a particle can also be created with enough energy in hand. But that is not all.



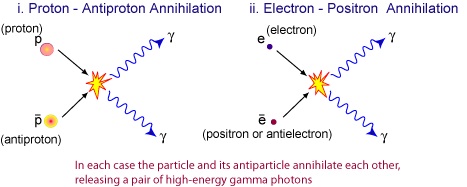
As we established in laboratory experiments on Earth, the only way to create matter is to take twice as much energy as the formula E = mc ² says , and create the same amount of matter and antimatter. And vice versa, we can destroy matter only by colliding it with antimatter, as a result of which pure energy is released. And all the laws of physics say that this is true at any time for any energies.

And yet, our universe is before us.



If we started with the Big Bang, then at the end of inflation, with all the necessary initial conditions and the known laws of physics, we would have such a state:

• The universe would be hot, dense, expanding, filled with radiation and equal shares of matter and antimatter.
• Matter and antimatter would collide, annihilate, turning into radiation, and high-energy particles would collide with each other, spontaneously creating new particles from matter and antimatter in equal proportions, with an excess of energy.
• The universe would expand and cool, while energy and density would fall.

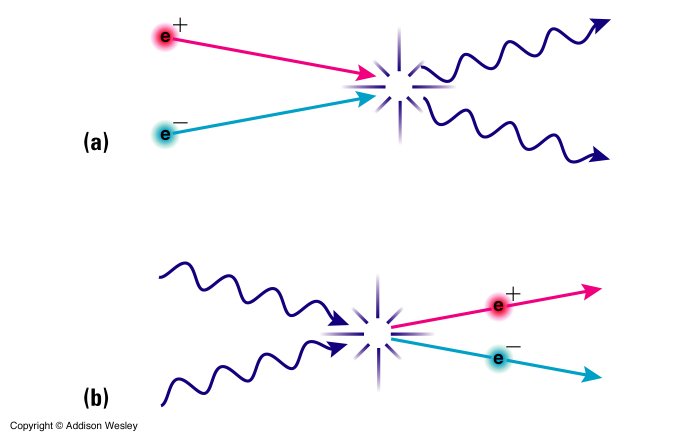
But, if energy falls, it becomes more difficult for high-energy particles to produce new matter / antimatter pairs (b), as a result of which the number of reactions that transform matter and antimatter into radiation decreases. But with a decrease in density, it becomes more difficult for the matter / antimatter pairs to find each other (a), as a result of which the number of these meetings will not drop to zero. There will always be remnants of matter and antimatter.

And here strange things begin. According to all calculations, based on the known laws of physics and our experiments, there should be 10 ²⁰ particles of radiation for each particle of matter or antimatter. But in our universe there are only a billion of them, 10 ⁹ pieces, per one particle of matter. And antimatter is generally very small.



So where did the excess matter come from? Why did excess matter appear, but not antimatter? And when? And How?

Honestly, this is one of the biggest unsolved mysteries of physics. But if we don’t know everything, this does not mean that we don’t have any clues at all. For example, since the 1960s it is known that by satisfying the following three conditions:

1. lack of balance
2. baryon number nonconservation
3. violation of C and CP invariance

more matter can be created than antimatter (or vice versa). Moreover, asymmetry in this case is simply inevitable. And, fortunately, two of these criteria are easy to satisfy.



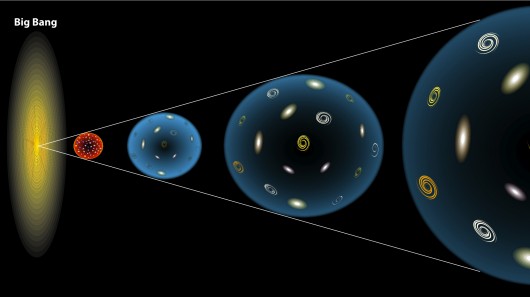
"Lack of balance" occurs when certain events in one part of the system do not affect the other part, since the information does not have time to reach them. An expanding Universe is an excellent example of a system in which, by definition, there is no equilibrium, and the above description of the appearance and annihilation of matter and antimatter during the expansion and cooling of the Universe is an excellent example of a nonequilibrium process.



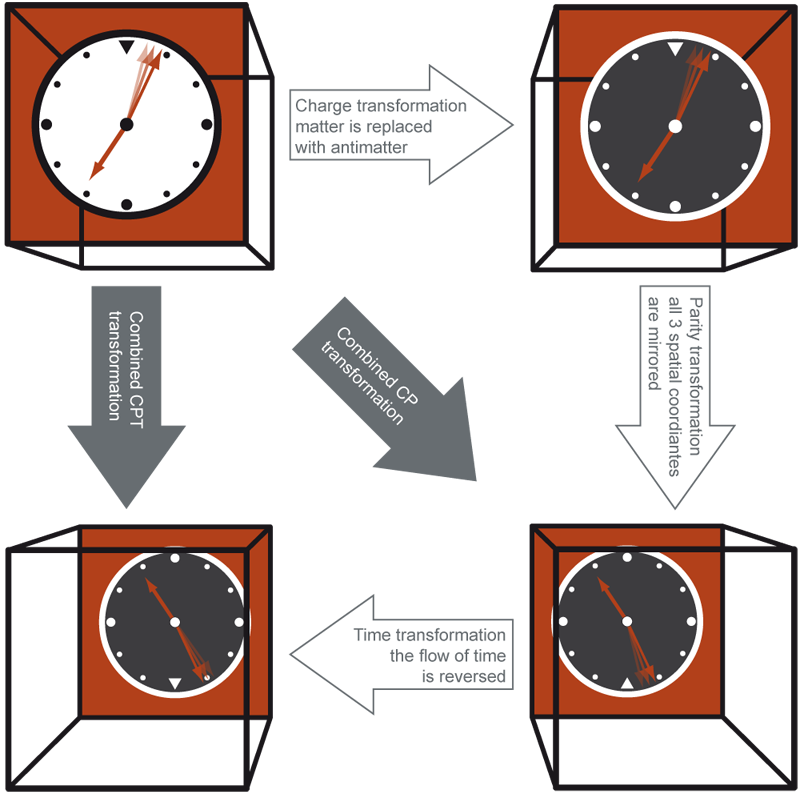
There are also many examples of the difference between matter and antimatter, and the breaking of various symmetries. One of them is charge conjugation symmetry, or C-symmetry. If you replace all particles with antiparticles, and the C-symmetry is preserved, then the system will behave exactly the same. Another is parity symmetry, P-symmetry. If it is preserved, then the real system and its mirror reflection should behave identically.



An unstable particle like a spinning muon decays in a specific way - by emitting an electron in a certain direction according to the spin. If you reflect this in the mirror (P), then the electron will be emitted in the opposite direction, which in life does not happen. If you replace the muon with an anti-muon (C), it will emit a positron in the original direction - and this also does not happen. But if we replace the rotating muon with a mirror copy of the rotating anti-muon (C and P, SR), we would hope that its decay should occur as reliably as the decay of the muon in the real (non-mirror) world. But this does not happen. There are other examples of the violation of C and CP symmetries in k-meson or B-meson systems.



Therefore, we only need to get interactions that do not preserve the baryon number in sufficient quantities, in other words, create baryons where they were not (but there was something else). Unfortunately, we need physics here that is not in the Standard Model.

But there are plenty of such mechanisms:

• grand unification theories containing GUT-scale particles
• theories with new scalars containing Affleck-Dyne mechanisms
• extensions to the Standard Model including heavy sterile neutrinos
• theory of excess leptons in the young Universe (leptogenesis)
• new electroweak physics that can improve the asymmetry between matter and antimatter

I will tell you in detail only one example.

Imagine a hot, dense, young Universe. In addition to the radiation and particles of matter and antimatter included in the Standard Model, there is another particle (and antiparticle), Q (and anti-Q). Q is very heavy, heavier than a proton, has a positive charge of +1 (like a proton) and appears in abundance in the young Universe, together with its halves, anti-Q, which have the same mass and opposite charge.

Since they are unstable, when the universe cools down, they will cease to be created. Most of them will find each other and annihilate, and the rest will decay.



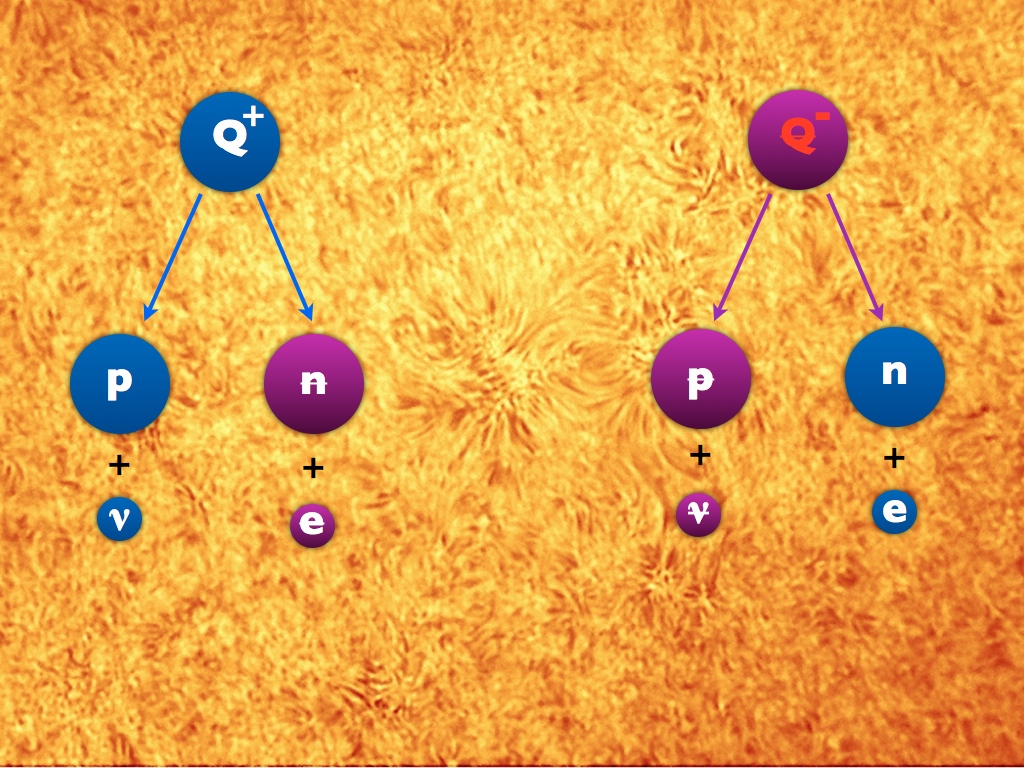
For each variant of Q decay, an appropriate decay of anti-Q must occur. If Q decays into a proton and neutrino, anti-Q must decay into an antiproton and antineutrino. If Q decays into an antineutron and positron, anti-Q must decay into a neutron and an electron.

These are not real particles, they are given as an example. But in different theories there are particles like the X-and-Y bosons in the GUT and the leptoquarks in some extensions of the Standard Model that work according to very similar rules.

In the absence of violation of CP symmetry, they will decay in the same way as their opposite.



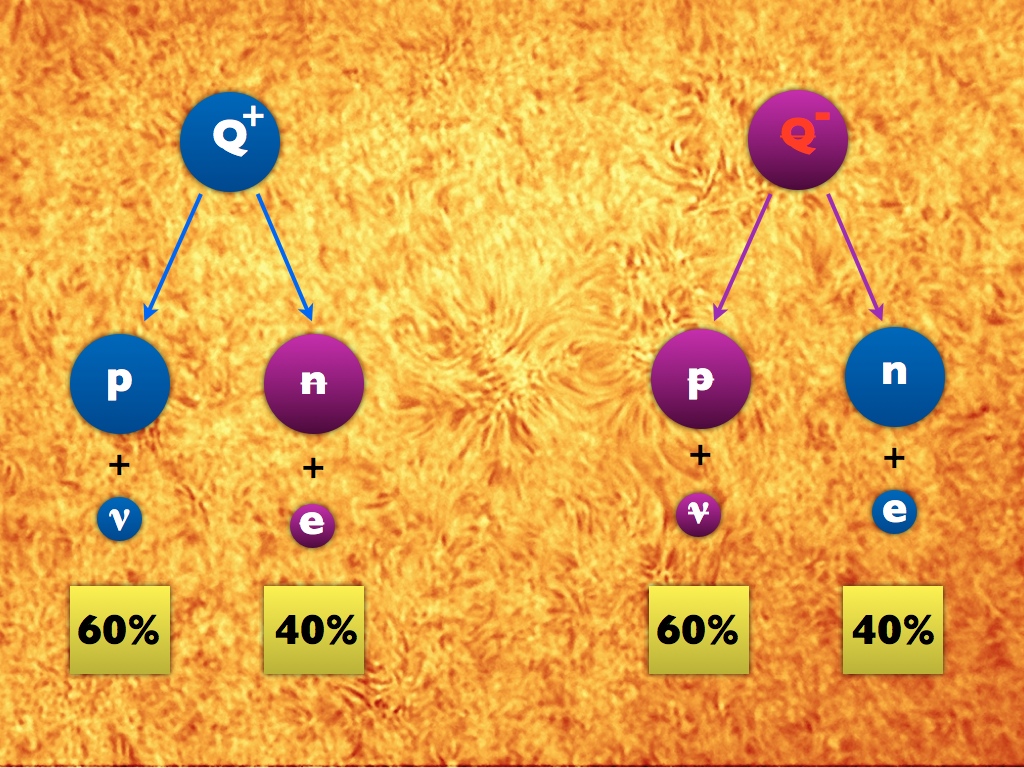
While all this is boring, this process will not create excesses of mass. But if we allow violation of CP symmetry, then the difference between particles and antiparticles can be in the number of decays. What percentage of Q decays into protons and neutrinos, compared with what percentage of anti-Q decays into antiprotons and antineutrinos. We may get something similar to the following picture, which is similar to what we observe in systems with Kaons and B-mesons. Notice the difference between Q decays and anti-Q.



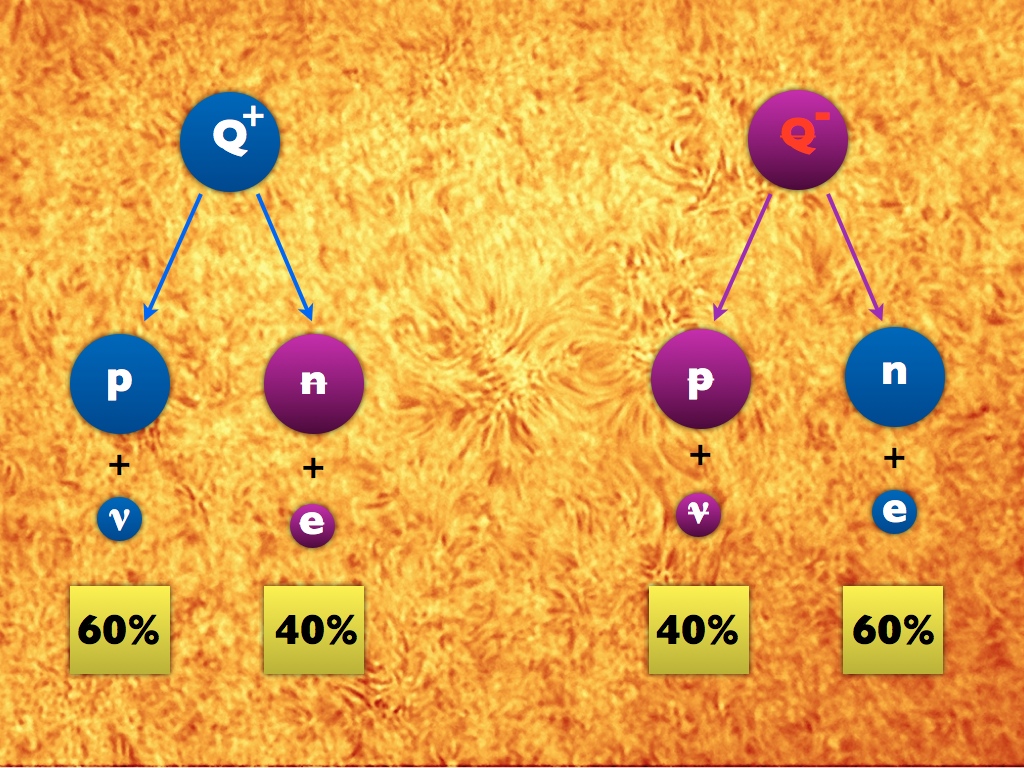
Suppose that our Universe is full of matter and antimatter in equal proportions, and radiation, which we ignore. Suppose also that there are a bunch of Q and anti-Q in equal amounts that break up in accordance with the CP symmetry violations described above.

What will be left?

A sea of ​​protons, neutrinos, antineutrinos, positrons, antiprotons, antineutrinos, neutrons and electrons. That is yes. But there will be more protons and neutrinos than antiprotons and antineutrinos, and there will be less antineutrons and positrons than neutrons and electrons. If we ignore leptons (neutrinos, electrons and their antiparticles), then this is what the sea of ​​decaying Q and anti-Q particles will leave us.



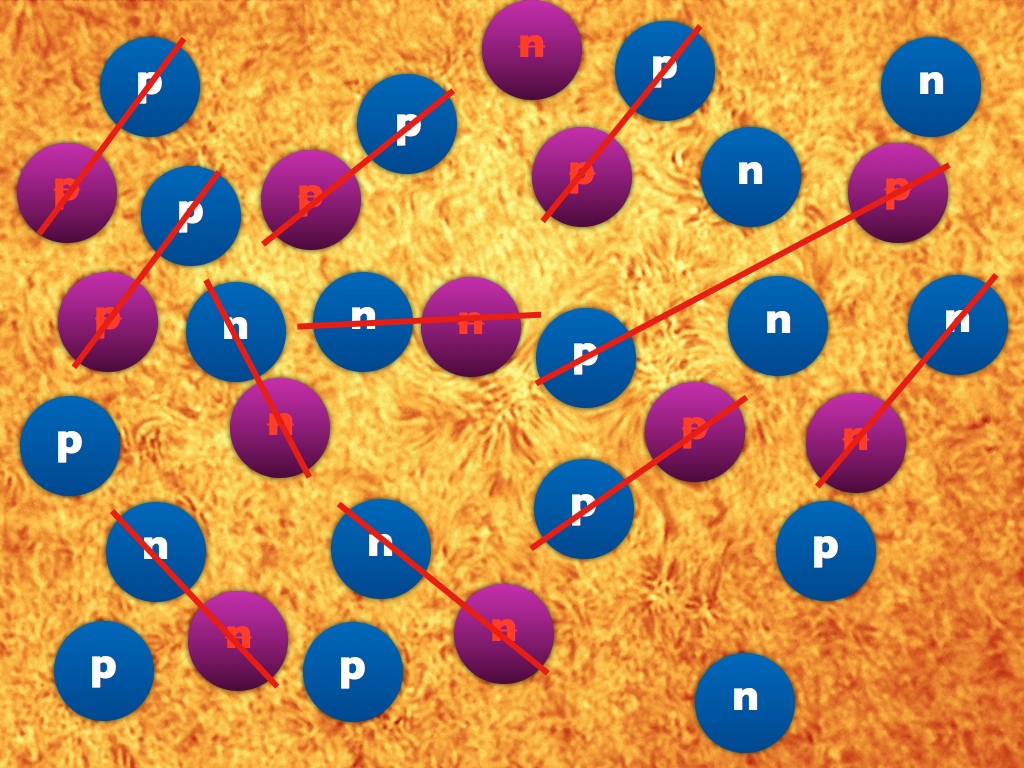
And after all the pairs of matter and antimatter meet, there will remain an excess of matter compared with antimatter.

A variant of such a development of events unambiguously took place and led to the fact that we have different amounts of matter and antimatter, and that the density of matter (but not antimatter) is the same everywhere we look. Even despite the fact that this is one of the greatest unsolved problems in physics, we know a lot about it, and this is worthy of retelling.