Kenneth Snelson's Chemistry (Part I)
When substantiating the properties of atoms and molecules, it is customary to refer to the postulates of quantum mechanics, which far from all physicists understand. Moreover, chemists who have the principles of Pauli and Heisenberg, the rules of Klechkovsky and Hund, and even the Schrödinger equation do not cause any feelings, except for a feeling of deep respect for the aforementioned physicists. It is even worse for humanities and other artistic natures who are useless to describe and explain such principles, rules and equations. As a result, one of them - the artist Kenneth Snelson (Kenneth Snelson; 06/29/1927 - 12/22/2016) - decided that "saving the drowning is the work of the drowning themselves." And in 1960, he came up with a simple theory of the structure of the atom, to which he devoted several dozen of his paintings, and even sculpted from granite / 1 /.

Fig. 1. “Atomic” sculptures (4'x4'x4 ', granite, 2009) / 1 / The
electrons in the Snelson atomic model have a ring shape and form spherical electron shells consisting of contiguous electron rings (“circle-sphere”). Snelson built models of such “cyclospheres” from ferrite ring magnets. If they are located on the surface of a sphere, then when alternating the direction of the magnetic field, the edges of adjacent magnets are attracted to each other, and their outer planes form polyhedral (ring-shaped) shells.

Fig. 2. Magnetic models of Snelson’s electronic shells
The most stable “electronic” structures are obtained from two, eight, ten and fourteen magnets.
According to Snelson's theory, such stable combinations of magnets correspond to the four main types of filled atomic shells constructed of ring electrons. The first type (2e - ) corresponds to helium, whose atomic radius is 31 pm. The second (8e - ) is characteristic of noble gases trailing periods in the periodic table (Ne - 38 pm; Ar - 71 pm; Kr - 88 pm; Xe - 108 pm; Rn - 120 pm). Larger filled shells (10e - ) are possessed by elements of the nickel subgroup (Ni - 149 pm; Pd - 169 pm; Pt - 177 pm). A shell of 14 electrons can form in lanthanides (Er - 226 pm) and, possibly, in actinides. In this case, the grouping of chemical elements by the types of outer electron shells of atoms reflects their division into small (8e -) and large (10e - + 8e - or 14e - + 10e - + 8e - ) periods of the periodic table.
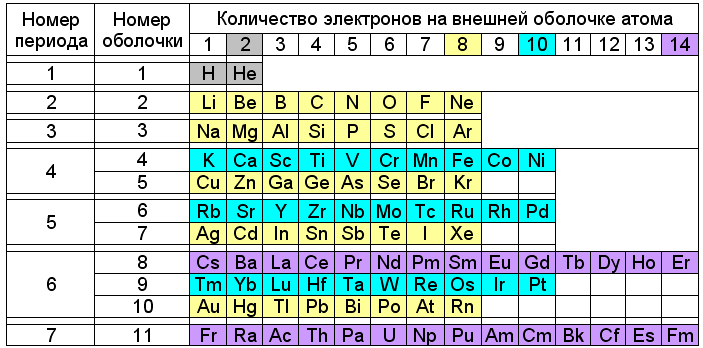
Fig. 3. Mendeleev's table with division of periods according to Snelson.
The position of some elements in this table looks unusual. For example, sodium, rubidium and cesium, despite the similarity of chemical properties, appear in different rows of colors - yellow (8e - ), blue (10e - ) and lilac (14e - ). And copper, silver and gold are colored the same way lithium and sodium are yellow. But it must be taken into account that the outer electrons of the elements from lithium to neon and from sodium to argon form eight-electron shells, and from potassium to nickel and from copper to krypton, they form ten-electron shells. On the same basis, elements from copper to krypton, from silver to xenon and from gold to radon are highlighted in yellow, and blue - from rubidium to palladium and from thulium to platinum.
In this case, the chemical properties of elements with one electron on the outer shell are determined by the type of underlying filled electron shell - eight-electron for alkali metals and ten-electron for copper, silver and gold.
The radii of atoms in the periodic table change periodically - they increase spasmodically during the transition to each subsequent period, but decrease inside the periods.
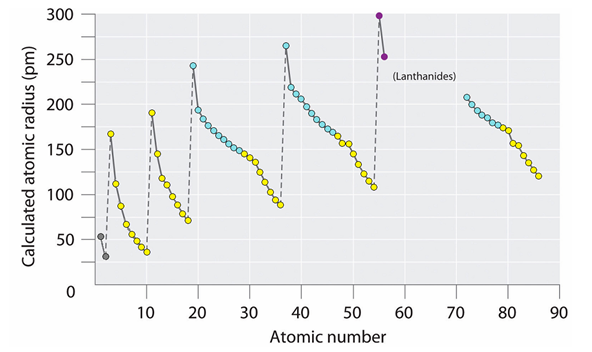
Fig. 4. Periods of atomic radii reference (with modifications)
It follows that the radii of ring electrons in atoms are also variable and depend on the distance to the atomic nucleus, its charge and type of electron shell. On the outer shell they are maximum, and especially large at the beginning of the period when the charge of the atomic nucleus (for a given period) is minimal. In this case, the type of filled electron shell depends on the atomic radius. If it is not more than 120 pm, then eight-electron shells are obtained. If more than 140 pm, then ten-electron. The construction of a filled shell for larger lanthanides (> 200 pm) requires no less than 14 electrons.
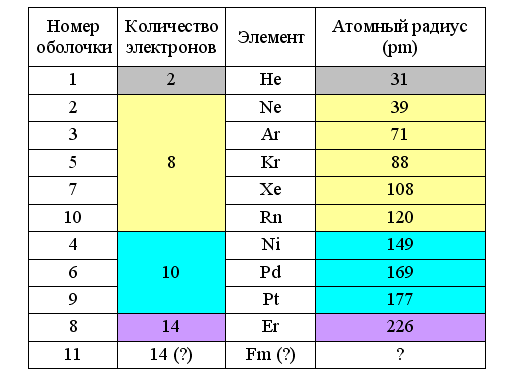
Fig. 5. Radii of atoms with filled electron shells ( link )
In the periodic table with periods separated by Snelson, the position of the noble gases with completed eight-electron shells looks quite logical. Logically, it looks and elements filled with ten-electron shells. These are silver metals, characterized by high chemical resistance and ductility (nickel, palladium and platinum). But the construction of the 14-electron shell of lanthanides should be completed in erbium, which is no different from previous dysprosium and holmium, nor from thulium, yttrium and lutetium following it. But on the transition from lutetium to hafnium, there is a sharp increase in density - from 9.85 to 13.2 g / cm3. Apparently, only at this stage, due to a decrease in the atomic radius, it becomes possible to form a stable 14-electron shell. And during its formation, “extra” external electrons remain. Therefore, in nature there does not exist an element with a 14-electron complete outer shell, noticeably different in chemical properties from neighboring elements.
The cyclospheric theory of the structure of electron shells of atoms, proposed by Snelson, is in good agreement with the periods of the periodic table, so it would be interesting to evaluate its consistency with the properties of molecules.
The outer shell of eight electrons, which is characteristic of noble gases, can possess even simple molecules containing hydrogen. For example, a methane molecule (CH 4 ). Usually in its models hydrogen is designated by a hemisphere or a separate ball. In the cyclospheric (ring-faceted) model, the eight-electron shell of methane consists of four ring electrons of the outer shell of the carbon atom and four hydrogen atoms (protonated electrons).
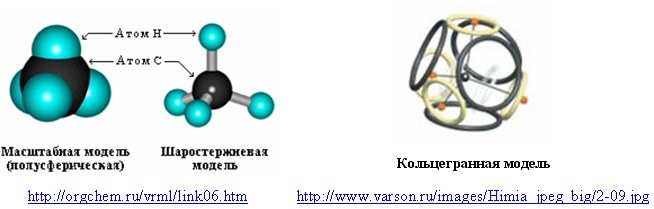
Fig. 6. Methane molecule models
Attraction of “hydrogen” electrons to protons reduces their diameters, and repulsion of protons from a positively charged nucleus pushes them slightly out of the plane of electron rings. But if you make the electrons invisible and connect the carbon nucleus with proton lines, then the ring-shaped model of the methane molecule will take on a classic form - symmetrical, with the same angles (109.5 °) between all hydrogen atoms.

Fig. 7. The structure of the methane molecule
. Ring-shaped electron shells of the anion of borohydride (BH 4 - ) and ammonium cation (NH 4 + ) may look approximately the same . But borohydride should be slightly larger, and ammonium slightly less than methane.
The ammonia molecule (NH 3 ) also has an eight-electron shell , although the loss of one ammonium proton deprives it of a positive charge, violates the symmetry and slightly changes the angles of the three remaining protons. And the same electron shell, but slightly smaller in diameter, should be at the hydroxonium cation (H 3 O + ).
Using the same principle, it is possible to construct an eight-electron shell of a water molecule, in which the angle formed by the oxygen nucleus and two protons will be even smaller.
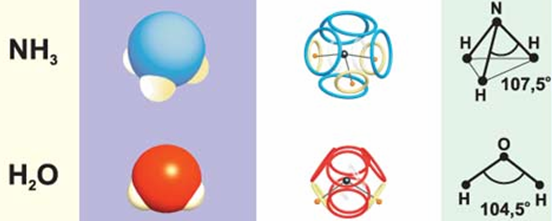
Fig. 8. Models of ammonia and water molecules / 2 / ( picture )
Thus, a number of simple molecules and ions with eight-electron shells can be distinguished, in which the shortage of external electrons is compensated by hydrogen atoms (protonated electrons). For elements of the second period, these are BH 4 - , CH 4 , NH 4 + , NH 3 , H 3 O + , H 2 O, OH - , HF and F - . Neon closes the second period, which does not require protons to neutralize the total negative charge of the electrons of the outer shell of the atom.
The same principle is used to construct external eight-electron shells for SiH 4 , PH 3 , SH 2, and HCl molecules formed by elements of the third period of the periodic table. Hydrogen atoms involved in the construction of electron shells of such molecules and ions affect their shape and chemical properties, but do not change the general structure.
In all such models, the relative positions of heavy nuclei with an internal electron shell and “bare” protons are in good agreement with the long-known “canonized” structures of these simple molecules. And according to Snelson's theory, the relative position of the central nucleus and protons is explained by the stability of the eight-electron outer shells of similar molecules formed by atoms of the second and third periods of the periodic table.
The similarities and differences in the electron shells of such simplest molecules reflect (well explain) their well-known structural parameters, but things can be more complicated with water molecules. In addition to the usual "meta-water", in which the protons are located at an angle of 104.5 °, there should also be "para-water", in which the protons lie on one straight line with the oxygen nucleus (180 °). Moreover, in "meta-water" the nuclei of hydrogen atoms (protons) can be either in the "northern" (N) or in the "southern" (S) electrons. In “para-water” such magnetic isomerism is absent, since its proton-containing electrons have the opposite (with respect to the center of the molecule) orientation of the magnetic field.
The structural and magnetic isomerism of the electron shells of water molecules in cyclospheric models contradicts its generally accepted descriptions. This could serve as evidence of the fallacy of Snelson's theory if it were not for the amazing variety of properties of water, which cannot be explained within the framework of generally accepted ideas about the only version of its molecular structure.
Magnetic isomerism should be characteristic of electron shells and many other molecules. But this topic, like the theoretical justification of the properties of water, is best discussed separately.

Fig. 9. Magnetic isomers of the simplest molecules (grommet models of electron shells)
Numerous carbon compounds deserve special consideration, in which the electron shells should noticeably differ from the shells of the simplest molecules described above.
Compounds consisting only of carbon are characterized by an extraordinary variety of molecular structures forming materials with unique properties (carbine, graphene, fullerene, nanotubes, diamond, etc. / 3 /). After the Nobel Prizes were awarded to the discoverers of fullerene (1996; R. Curl, H. Kroto, R. Smolly) and graphene (2010; A.K. Geim, K.S. Novosyolov), predictions and searches for new forms gained great popularity carbon. As a result of such predictions, molecules of carafe, grafdin, fagrafen and other predominantly hypothetical carbon compounds were described.
Carbin is the simplest structure - a linear carbon polymer / 4 /. The assembly of the model of its electron shell is not difficult, since there are four electrons on the outer shell of the carbon atom. These electrons form a “cube” with two unfilled faces. The assembly of such "cubes" of linear polymer gives carbin.

Fig. 10. Carbine The
high brittleness of carbine allows it to bend and form closed rings. Due to the obligatory alternation of the poles of the magnetic field of adjacent electrons, rings can contain only an even number of carbon atoms. Especially stable should be rings with six carbon atoms (hexamers, C 6 ), the electrons of which can connect at different angles and form electron shells of various types. The most famous structures form the "Nobel" molecules - graphene and fullerene. It is not difficult to build models of electron shells of the Snelson type for them, if one uses different types of compounds of hexameric carbon rings — graphene (2D) and fullerene (3D).

Fig. 11. The main 2D and 3D forms of carbon
Fullerenes got their name in honor of the prominent American architect, designer and inventor Richard Fuller. But a great contribution to the theory of the famous Fuller was made by his less famous collaborator and no less talented inventor Kenneth Snelson. Therefore, it would be nice to assign some other undiscovered carbon molecules to his name. Moreover, Snelson's theory allows not only to describe the already known forms of carbon, but also to predict its varieties not yet known to science. Many such structures can be built, but they are usually distinguished not only by increased flexibility and fragility, but also by the ability to form linked three-dimensional conglomerates, which makes it difficult to isolate individual chemicals from a mixture of close structural analogues.
It is possible to build electron shells of the Snelson type for the most durable form of carbon - diamond. Moreover, not only for its usual variety, but also for a more rare and poorly studied form - lonsdaleite.

Fig. 12. The structure of diamond electron shells The diamond
crystal lattice can be considered a three-dimensional polymer of methane, in which all hydrogen atoms are replaced by carbon-carbon “hole” bonds. Each carbon atom is surrounded by four electrons and four interatomic bonds, and there are small gaps between the electron shells of individual atoms. In this case, each electron is linked to six neighboring electrons.
In a lonsdaleite crystal, carbon atoms have eight-electron shells, and all the electrons that form them serve as interatomic walls (“electronic” bonds). As a result, there are four “whole” electrons for each carbon atom. More precisely - eight of their "halves", divided between adjacent atoms. Lonsdaleite, unlike ordinary diamond, has no interatomic spaces. Moreover, each electron is also associated with six neighboring electrons.
Crystals of other especially hard substances, such as moissanite (SiC), borazon (γ-BN) and boron phosphide (BP), can have similar structural variants of electron shells. The high hardness of all such compounds is well explained by the structure of their electron shells, in which each electron is bonded to six neighbors. In ordinary molecules, electrons have no more than four such bonds.
The Snelson theory of the structure of molecular electron shells explains well the diversity of allotropic forms of carbon, but to prove its universality it is advisable to test this theory on other carbon compounds. First of all, on well-studied hydrocarbons.
Alkanes, i.e. saturated hydrocarbons with the general formula C n H 2n + 2 can be considered derivatives of methane, in which some proton electrons are replaced by “hole” carbon-carbon bonds. The three simplest molecules of this type include ethane, propane, butane and isobutane.

Fig. 13. Models of electron shells of the simplest alkanes
Propane and other alkanes having an odd number of carbon atoms in an unbranched chain are characterized by magnetic isomerism. In linear saturated hydrocarbons with an even number of carbon atoms, magnetic isomerism is absent. And with an increase in the number of carbon atoms in a molecule, the number of magnetic, structural, and rotational isomers (rotamers) increases exponentially.

Fig. 14. Magnetic, structural and rotational isomers of pentane.
Even more isomers can be constructed for hexane, but this does not apply to cyclic saturated hydrocarbons. For example, cyclohexane has no magnetic isomers, although if we consider the layout of its electron shell from the side, we can see that the unidirectional spins of the upper and lower electrons have opposite orientations.

Fig. 15. The model of the electron shell of cyclohexane (C 6 H 12 ) (two sides of the same “coin”)
The original electron shell has a benzene molecule (C 6 H 6 ) containing six symmetric planarly arranged hydrogen atoms. Build a shell of hexamer C 6characteristic of graphene or fullerene is impossible. But it is easily built on the basis of a ring of six linked electrons forming a central hexagonal cylinder. In this design, for each carbon atom there are five electrons - four proper and one "hydrogen". Such a structure explains the low density of benzene (0.876 g / cm³), the symmetry of the molecule’s structure, the planar arrangement of hydrogen atoms, and their ability to be replaced by radicals, which lack one electron to complete the octahedral shells.

Fig. 16. The electron shell of a benzene molecule. Five
-membered ring electron compounds characteristic of benzene carbon atoms are repeatedly found in Snelson's paintings, and it would be strange if they were absent in chemical compounds.

Fig. 17. Five-electron shells of Snelson / 1 /
Based on the above-described variant of the electronic shell of benzene, it is possible to construct shells for its many derivatives with various side radicals, as well as with nitrogen atoms, partially or completely replacing the carbon of the central ring.

Fig. 18. Models of the electron shells of the simplest derivatives of benzene
The outer electronic shell of ethylene (C 2 H 4 ), the simplest representative of alkenes (C n H 2n ), is easily constructed from eight ordinary and four protonated electron rings. Similar 12-electron shells can have molecules of diimide (N 2 H 2 ), oxygen (O 2 ), and formaldehyde (CH 2 O).

Fig. 19. Models of molecules with 12-electron shells.
All other alkenes, dienes, and trienes can be considered alkanes containing one, two, or three ethylene groups.
Hydrocarbons belonging to alkynes (C n H 2n-2 ) contain a pair of carbon atoms joined by an elongated 10-electron shell. For each carbon atom there are four electrons, therefore, the missing positions in acetylene are built up by two hydrogen atoms, and in the remaining alkynes these hydrogens are replaced by one or two “hole” bonds with the electron shells of neighboring atoms.
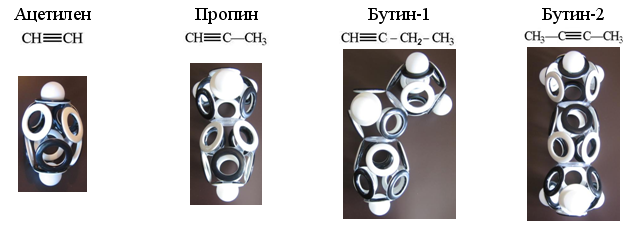
Fig. 20. Models of the electron shells of the simplest alkynes
Thus, for all the main types of hydrocarbons — alkanes, arenes, alkenes, and alkynes — it is possible to construct models of the external electron shells that satisfy all the canons of Kenneth Snelson's theory. Moreover, such shells can serve as samples for molecular prototyping of compounds containing not only carbon atoms. Illustrative examples are the 12-electron shells described above for analogs of ethylene — diimide, oxygen, and formaldehyde. By analogy with them, it would be interesting to consider the Snelson shells of more complex molecules containing 10-electron structures of the acetylene type.
The spherical shell, built of ten electronic rings, is able to stretch in different directions. Best of all - along the axis of symmetry passing through a pair of electrons located at the "poles". For chemically unstable acetylene (C 2 H 2 ), this axis passes through hydrogen atoms. Molecular nitrogen (N 2 ), which is characterized by chemical resistance , has no hydrogen atoms, and the elongated electron shell is characterized by increased strength. A similar Snelson 10-electron shell can also be constructed for some other simple molecules.

Fig. 21. Models of 10-electron shells of the simplest molecules
More complex electronic shells containing inserts of 10-electron elements can have molecules of urea, acetone, acetamide, carbonic and acetic acids, as well as guanidine. A characteristic feature of all molecules of this type is their magnetic isomerism and the presence of interatomic bonds with electronic inserts ("electronic" bonds).

Fig. 22. Models of shells of molecules with 10-electron central groups.
Especially often in organic compounds there is a 10-electron group of carbon monoxide (CO). Some heterocyclic compounds contain two, three or even four such groups.

Fig. 23. Examples of heterocycles with 10-electron CO groups
A characteristic feature of the electron shells of such molecules is the presence of lonsdaleite type atomic bonds (with insertions of interatomic electrons). Similar "electronic" bonds can be present in many other molecules. For example, for polyiodides (I 3 - , I 5 - , I 7 - , I 9 - and others), crystallizing from solutions containing iodides (I - ) and iodine (I 2 ) / 5 /.

Fig. 24. The model of the electron shell of anion I 3 - with interatomic bonds of the Lonsdaleite type
It would be very interesting to analyze the structure of the electron shells of numerous halogen compounds, but only for a limited circle of chemists. Therefore, it is better to verify the correctness of the theory proposed by Snelson by constructing the electron shells of more well-known molecules - proteins, DNA, etc.
The main structural element of all protein molecules is the peptide bond. The coincidence of its known parameters with the parameters of the ring-shaped electron shell can serve as a good proof of the correctness of Snelson's theory. And the discrepancy is a refutation.
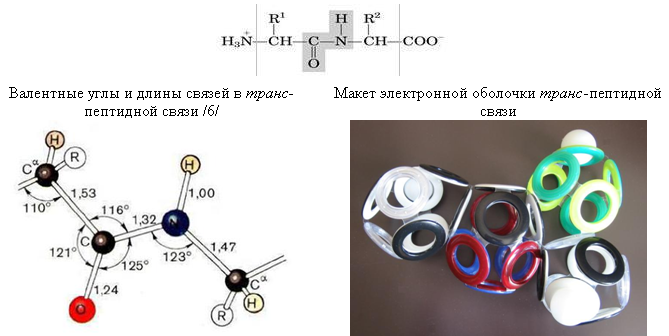
Fig. 25. Peptide bond. The
grommet displays only the electron shell, which does not allow precise determination of the angles between the centers of atoms. Nevertheless, their general arrangement is consistent with the schemes from the textbooks / 6 /. For example, the layout clearly shows the planarity of the three bonds of the peptide nitrogen atom, which in most of its compounds are pyramidal. Such planarity can be explained by the presence of an interatomic electron between the 10-electron shell of CO and the octagonal shell of the nitrogen atom. This electron is adjacent to the NC (“hole”) bond unfilled by the electron (denoted by a transparent grommet), and in this case the opposite face of the shell of the nitrogen atom becomes the most stable position for the protonated electron (hydrogen atom).
The decrease in the length of the peptide bond (CO) -N (1.32 Å) compared with the length of the single bond CN (1.47 Å) can also be explained by the presence of an interatomic (“lonsdaleite”) electron in it. Thus, in the layout of the electronic shell of the peptide bond constructed in accordance with the Snelson theory, there are no fundamental discrepancies with generally accepted ideas about its structure.
The construction of ring-shaped electron shells is apparently also applicable for modeling the spatial structure of proteins, but for large molecules it is more convenient to use not cringles and similar models, but computer 3D modeling. Attempts to such modeling are discussed in detail in the recently published monograph / 7 /.
Another proof of the correctness of Snelson's theory can be built on the layout of the electron shells of the four bases of DNA. And to demonstrate the presence of hydrogen bonds in pairs of complementary bases of AT and GC.
When describing the electron shells of these nitrogenous bases, it is desirable to adhere to the generally accepted numbering of the pyrimidine (C and T) and purine (A and G) nitrogen base atoms shown in the figure.

Fig. 26. Nitrogen bases of DNA
A characteristic feature of the structure of the bases C, T, G, and A, as well as their pairs in the DNA, is planarity. It follows that at least some of the bonds of nitrogen atoms in these bases can be either identical or similar to the planar peptide bond CO-N.
The planarity of bonds is also characteristic of the ten-electron pairs -CH = CH- and -CH = N- that form benzene, which are part of such benzene analogues as pyrimidine and pyrazine. There are two ten-electron pairs of benzene type atoms in cytosine (C 5 -C 6 , N 3 -C 4 ), in thymine one (C 5 -C 6 ), in adenine four (C 4 -C 5 , N 1 -C 6 , C 2 -N 3 , N 7 -C 8 ) and guanine have three (C 4 -C 5 , C 2 -N 3 , N 7 -C8 ).
It is easy to get confused in the various bonds of purine and pyrimidine heterocycles, so it is better to consider them on the models of electronic shells.

Fig. 27. Models of electronic shells of nitrogenous bases (the oxygen atom of deoxyribose is denoted by an eight-electron shell of transparent grommets).
At least five types of interatomic bonds are found in ring-shaped electronic shells of nitrogenous bases:
• electronic (lonsdaleite type, with an atomic electron insert);
• hole (without electronic insert);
• benzene (bonds -C = C- and -N = C- with pairs of five-electron shells);
• ten-electron (СО);
• fan (four electronic rings linked at one point).
For example, cytosine has four electronic bonds (N 1 -C 2 , C 4 -C 5 , C 4 - (NH2 ) and C 6 -N 1 ), one hole (N 1 -dRib), two benzene (N 3 -C 4 , C 5 -C 6 ), one ten-electron (C 2 O) and one fan (C 2 -N 3 ). Thymine has four electronic bonds (N 1 -C 2 , C 2 -N 3 , N 3 -C 4 and C 6 -N 1 ), two hole (C 5 - (CH 3 )) and N 1 -dRib), one benzene (C 5 -C 6), two ten-electron (C 2 O, C 4 O) and one fan (C 4 -C 5 ). All this, of course, is interesting, but it would be more interesting to look at the presence of hydrogen bonds in complementary pairs of nitrogenous bases.
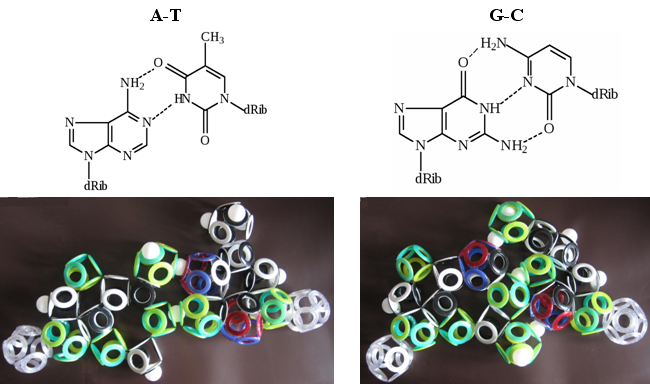
Fig. 28. Nitrogen base complementarity
On grommet models of Snelson electron shells, two hydrogen bonds in the AT pair and three in the GC are clearly visible. This is unlikely to be a mere coincidence. And for those who understand the intricacies of DNA structure, this can serve as an indisputable proof of the correctness of Kenneth Snelson's theory. The only stumbling block for them will be the magnetic isomerism of the electron shells of all biomolecules, which does not fit into modern ideas about their structure.
Magnetic isomers of biomolecules can hardly be distinguished by any physical methods, but their organoleptic properties should differ greatly, which can be demonstrated by the example of magnetic isomers of ethanol (C 2 H 5 OH).

Fig. 29. Magnetic isomers of ethanol.
As you know, even the highest purity ethanol, diluted to a standard concentration of 40%, is practically impossible to drink without a snack and in an uncooled form. But fresh moonshine of the same concentration is drunk even warm. An appetizer in this case will not be superfluous, but if you drink a little, you can do without it. Any chemist with basic equipment is capable of checking this. And not even a chemist, if he prefers to rely on his own experience and has a moonshine.
Snelson's theory allows one to explain this fact by preserving the magnetic isomerism of ethanol in fresh moonshine and racemizing its molecules in purified alcohol, but quantum mechanics is powerless here. But do not dissuade connoisseurs of quantum mechanics with such examples. They don’t understand.
The theory of the structure of the electron shells of atoms and molecules, proposed by Kenneth Snelson, is unlikely in the near future to compete with quantum-mechanical concepts based on a harmonious system of postulates. The main postulate of this system - the Heisenberg uncertainty principle - could not be refuted even by Einstein, therefore, when meeting with experts in quantum mechanics, do not try to argue with them. And try not to smile. It annoys others.
1. Kenneth Snelson; Art and Ideas / In association with Marlborough gallery, NY, 2013, NY, 174 R. http://kennethsnelson.net/KennethSnelson_Art_And_Ideas.pdf
2. Kozhevnikov D.N. The creation and use of a complex of models of atoms and molecules to study the structure of matter in a chemistry course in high school // Diss. for the competition degrees of cand. ped Sciences, 2004. - 171 p.
3. Haimann RB, Evsyukov S.E. Allotropy of carbon // Nature. 2003. - No. 8. - p. 66-72.
4. Sladkov A. M., Kudryavtsev Yu. P. Diamond, graphite, carbine - allotropic forms of carbon // Nature. - 1969. - No. 5. - p. 37-44.
5. Ivanov D.M., Ivanov M.G. Chemistry of halogens // Textbook. - 2014. - Publishing House of the Ural University. - 82 p.
6. Ovchinnikov Yu.A. Bioorganic chemistry // 1987. - M .: Publishing house "Education", 814 p.
7. Sokolik VV, Kushelev A.Yu. The geometry of a living nanoworld. Protein picotechnology / Lambert Academic Publishing, 2016 .-- 292 p.
PS: A variant of the article in PDF format can be found here .

Fig. 1. “Atomic” sculptures (4'x4'x4 ', granite, 2009) / 1 / The
electrons in the Snelson atomic model have a ring shape and form spherical electron shells consisting of contiguous electron rings (“circle-sphere”). Snelson built models of such “cyclospheres” from ferrite ring magnets. If they are located on the surface of a sphere, then when alternating the direction of the magnetic field, the edges of adjacent magnets are attracted to each other, and their outer planes form polyhedral (ring-shaped) shells.

Fig. 2. Magnetic models of Snelson’s electronic shells
The most stable “electronic” structures are obtained from two, eight, ten and fourteen magnets.
Mendeleev's Snelson table
According to Snelson's theory, such stable combinations of magnets correspond to the four main types of filled atomic shells constructed of ring electrons. The first type (2e - ) corresponds to helium, whose atomic radius is 31 pm. The second (8e - ) is characteristic of noble gases trailing periods in the periodic table (Ne - 38 pm; Ar - 71 pm; Kr - 88 pm; Xe - 108 pm; Rn - 120 pm). Larger filled shells (10e - ) are possessed by elements of the nickel subgroup (Ni - 149 pm; Pd - 169 pm; Pt - 177 pm). A shell of 14 electrons can form in lanthanides (Er - 226 pm) and, possibly, in actinides. In this case, the grouping of chemical elements by the types of outer electron shells of atoms reflects their division into small (8e -) and large (10e - + 8e - or 14e - + 10e - + 8e - ) periods of the periodic table.

Fig. 3. Mendeleev's table with division of periods according to Snelson.
The position of some elements in this table looks unusual. For example, sodium, rubidium and cesium, despite the similarity of chemical properties, appear in different rows of colors - yellow (8e - ), blue (10e - ) and lilac (14e - ). And copper, silver and gold are colored the same way lithium and sodium are yellow. But it must be taken into account that the outer electrons of the elements from lithium to neon and from sodium to argon form eight-electron shells, and from potassium to nickel and from copper to krypton, they form ten-electron shells. On the same basis, elements from copper to krypton, from silver to xenon and from gold to radon are highlighted in yellow, and blue - from rubidium to palladium and from thulium to platinum.
In this case, the chemical properties of elements with one electron on the outer shell are determined by the type of underlying filled electron shell - eight-electron for alkali metals and ten-electron for copper, silver and gold.
The radii of atoms in the periodic table change periodically - they increase spasmodically during the transition to each subsequent period, but decrease inside the periods.

Fig. 4. Periods of atomic radii reference (with modifications)
It follows that the radii of ring electrons in atoms are also variable and depend on the distance to the atomic nucleus, its charge and type of electron shell. On the outer shell they are maximum, and especially large at the beginning of the period when the charge of the atomic nucleus (for a given period) is minimal. In this case, the type of filled electron shell depends on the atomic radius. If it is not more than 120 pm, then eight-electron shells are obtained. If more than 140 pm, then ten-electron. The construction of a filled shell for larger lanthanides (> 200 pm) requires no less than 14 electrons.

Fig. 5. Radii of atoms with filled electron shells ( link )
In the periodic table with periods separated by Snelson, the position of the noble gases with completed eight-electron shells looks quite logical. Logically, it looks and elements filled with ten-electron shells. These are silver metals, characterized by high chemical resistance and ductility (nickel, palladium and platinum). But the construction of the 14-electron shell of lanthanides should be completed in erbium, which is no different from previous dysprosium and holmium, nor from thulium, yttrium and lutetium following it. But on the transition from lutetium to hafnium, there is a sharp increase in density - from 9.85 to 13.2 g / cm3. Apparently, only at this stage, due to a decrease in the atomic radius, it becomes possible to form a stable 14-electron shell. And during its formation, “extra” external electrons remain. Therefore, in nature there does not exist an element with a 14-electron complete outer shell, noticeably different in chemical properties from neighboring elements.
The cyclospheric theory of the structure of electron shells of atoms, proposed by Snelson, is in good agreement with the periods of the periodic table, so it would be interesting to evaluate its consistency with the properties of molecules.
Eight-electron shells of simple molecules
The outer shell of eight electrons, which is characteristic of noble gases, can possess even simple molecules containing hydrogen. For example, a methane molecule (CH 4 ). Usually in its models hydrogen is designated by a hemisphere or a separate ball. In the cyclospheric (ring-faceted) model, the eight-electron shell of methane consists of four ring electrons of the outer shell of the carbon atom and four hydrogen atoms (protonated electrons).

Fig. 6. Methane molecule models
Attraction of “hydrogen” electrons to protons reduces their diameters, and repulsion of protons from a positively charged nucleus pushes them slightly out of the plane of electron rings. But if you make the electrons invisible and connect the carbon nucleus with proton lines, then the ring-shaped model of the methane molecule will take on a classic form - symmetrical, with the same angles (109.5 °) between all hydrogen atoms.

Fig. 7. The structure of the methane molecule
. Ring-shaped electron shells of the anion of borohydride (BH 4 - ) and ammonium cation (NH 4 + ) may look approximately the same . But borohydride should be slightly larger, and ammonium slightly less than methane.
The ammonia molecule (NH 3 ) also has an eight-electron shell , although the loss of one ammonium proton deprives it of a positive charge, violates the symmetry and slightly changes the angles of the three remaining protons. And the same electron shell, but slightly smaller in diameter, should be at the hydroxonium cation (H 3 O + ).
Using the same principle, it is possible to construct an eight-electron shell of a water molecule, in which the angle formed by the oxygen nucleus and two protons will be even smaller.

Fig. 8. Models of ammonia and water molecules / 2 / ( picture )
Thus, a number of simple molecules and ions with eight-electron shells can be distinguished, in which the shortage of external electrons is compensated by hydrogen atoms (protonated electrons). For elements of the second period, these are BH 4 - , CH 4 , NH 4 + , NH 3 , H 3 O + , H 2 O, OH - , HF and F - . Neon closes the second period, which does not require protons to neutralize the total negative charge of the electrons of the outer shell of the atom.
The same principle is used to construct external eight-electron shells for SiH 4 , PH 3 , SH 2, and HCl molecules formed by elements of the third period of the periodic table. Hydrogen atoms involved in the construction of electron shells of such molecules and ions affect their shape and chemical properties, but do not change the general structure.
In all such models, the relative positions of heavy nuclei with an internal electron shell and “bare” protons are in good agreement with the long-known “canonized” structures of these simple molecules. And according to Snelson's theory, the relative position of the central nucleus and protons is explained by the stability of the eight-electron outer shells of similar molecules formed by atoms of the second and third periods of the periodic table.
The similarities and differences in the electron shells of such simplest molecules reflect (well explain) their well-known structural parameters, but things can be more complicated with water molecules. In addition to the usual "meta-water", in which the protons are located at an angle of 104.5 °, there should also be "para-water", in which the protons lie on one straight line with the oxygen nucleus (180 °). Moreover, in "meta-water" the nuclei of hydrogen atoms (protons) can be either in the "northern" (N) or in the "southern" (S) electrons. In “para-water” such magnetic isomerism is absent, since its proton-containing electrons have the opposite (with respect to the center of the molecule) orientation of the magnetic field.
The structural and magnetic isomerism of the electron shells of water molecules in cyclospheric models contradicts its generally accepted descriptions. This could serve as evidence of the fallacy of Snelson's theory if it were not for the amazing variety of properties of water, which cannot be explained within the framework of generally accepted ideas about the only version of its molecular structure.
Magnetic isomerism should be characteristic of electron shells and many other molecules. But this topic, like the theoretical justification of the properties of water, is best discussed separately.

Fig. 9. Magnetic isomers of the simplest molecules (grommet models of electron shells)
Numerous carbon compounds deserve special consideration, in which the electron shells should noticeably differ from the shells of the simplest molecules described above.
Carbon electronic shells
Compounds consisting only of carbon are characterized by an extraordinary variety of molecular structures forming materials with unique properties (carbine, graphene, fullerene, nanotubes, diamond, etc. / 3 /). After the Nobel Prizes were awarded to the discoverers of fullerene (1996; R. Curl, H. Kroto, R. Smolly) and graphene (2010; A.K. Geim, K.S. Novosyolov), predictions and searches for new forms gained great popularity carbon. As a result of such predictions, molecules of carafe, grafdin, fagrafen and other predominantly hypothetical carbon compounds were described.
Carbin is the simplest structure - a linear carbon polymer / 4 /. The assembly of the model of its electron shell is not difficult, since there are four electrons on the outer shell of the carbon atom. These electrons form a “cube” with two unfilled faces. The assembly of such "cubes" of linear polymer gives carbin.

Fig. 10. Carbine The
high brittleness of carbine allows it to bend and form closed rings. Due to the obligatory alternation of the poles of the magnetic field of adjacent electrons, rings can contain only an even number of carbon atoms. Especially stable should be rings with six carbon atoms (hexamers, C 6 ), the electrons of which can connect at different angles and form electron shells of various types. The most famous structures form the "Nobel" molecules - graphene and fullerene. It is not difficult to build models of electron shells of the Snelson type for them, if one uses different types of compounds of hexameric carbon rings — graphene (2D) and fullerene (3D).

Fig. 11. The main 2D and 3D forms of carbon
Fullerenes got their name in honor of the prominent American architect, designer and inventor Richard Fuller. But a great contribution to the theory of the famous Fuller was made by his less famous collaborator and no less talented inventor Kenneth Snelson. Therefore, it would be nice to assign some other undiscovered carbon molecules to his name. Moreover, Snelson's theory allows not only to describe the already known forms of carbon, but also to predict its varieties not yet known to science. Many such structures can be built, but they are usually distinguished not only by increased flexibility and fragility, but also by the ability to form linked three-dimensional conglomerates, which makes it difficult to isolate individual chemicals from a mixture of close structural analogues.
It is possible to build electron shells of the Snelson type for the most durable form of carbon - diamond. Moreover, not only for its usual variety, but also for a more rare and poorly studied form - lonsdaleite.

Fig. 12. The structure of diamond electron shells The diamond
crystal lattice can be considered a three-dimensional polymer of methane, in which all hydrogen atoms are replaced by carbon-carbon “hole” bonds. Each carbon atom is surrounded by four electrons and four interatomic bonds, and there are small gaps between the electron shells of individual atoms. In this case, each electron is linked to six neighboring electrons.
In a lonsdaleite crystal, carbon atoms have eight-electron shells, and all the electrons that form them serve as interatomic walls (“electronic” bonds). As a result, there are four “whole” electrons for each carbon atom. More precisely - eight of their "halves", divided between adjacent atoms. Lonsdaleite, unlike ordinary diamond, has no interatomic spaces. Moreover, each electron is also associated with six neighboring electrons.
Crystals of other especially hard substances, such as moissanite (SiC), borazon (γ-BN) and boron phosphide (BP), can have similar structural variants of electron shells. The high hardness of all such compounds is well explained by the structure of their electron shells, in which each electron is bonded to six neighbors. In ordinary molecules, electrons have no more than four such bonds.
The Snelson theory of the structure of molecular electron shells explains well the diversity of allotropic forms of carbon, but to prove its universality it is advisable to test this theory on other carbon compounds. First of all, on well-studied hydrocarbons.
Electronic shells of hydrocarbons
Alkanes, i.e. saturated hydrocarbons with the general formula C n H 2n + 2 can be considered derivatives of methane, in which some proton electrons are replaced by “hole” carbon-carbon bonds. The three simplest molecules of this type include ethane, propane, butane and isobutane.

Fig. 13. Models of electron shells of the simplest alkanes
Propane and other alkanes having an odd number of carbon atoms in an unbranched chain are characterized by magnetic isomerism. In linear saturated hydrocarbons with an even number of carbon atoms, magnetic isomerism is absent. And with an increase in the number of carbon atoms in a molecule, the number of magnetic, structural, and rotational isomers (rotamers) increases exponentially.

Fig. 14. Magnetic, structural and rotational isomers of pentane.
Even more isomers can be constructed for hexane, but this does not apply to cyclic saturated hydrocarbons. For example, cyclohexane has no magnetic isomers, although if we consider the layout of its electron shell from the side, we can see that the unidirectional spins of the upper and lower electrons have opposite orientations.

Fig. 15. The model of the electron shell of cyclohexane (C 6 H 12 ) (two sides of the same “coin”)
The original electron shell has a benzene molecule (C 6 H 6 ) containing six symmetric planarly arranged hydrogen atoms. Build a shell of hexamer C 6characteristic of graphene or fullerene is impossible. But it is easily built on the basis of a ring of six linked electrons forming a central hexagonal cylinder. In this design, for each carbon atom there are five electrons - four proper and one "hydrogen". Such a structure explains the low density of benzene (0.876 g / cm³), the symmetry of the molecule’s structure, the planar arrangement of hydrogen atoms, and their ability to be replaced by radicals, which lack one electron to complete the octahedral shells.

Fig. 16. The electron shell of a benzene molecule. Five
-membered ring electron compounds characteristic of benzene carbon atoms are repeatedly found in Snelson's paintings, and it would be strange if they were absent in chemical compounds.

Fig. 17. Five-electron shells of Snelson / 1 /
Based on the above-described variant of the electronic shell of benzene, it is possible to construct shells for its many derivatives with various side radicals, as well as with nitrogen atoms, partially or completely replacing the carbon of the central ring.

Fig. 18. Models of the electron shells of the simplest derivatives of benzene
The outer electronic shell of ethylene (C 2 H 4 ), the simplest representative of alkenes (C n H 2n ), is easily constructed from eight ordinary and four protonated electron rings. Similar 12-electron shells can have molecules of diimide (N 2 H 2 ), oxygen (O 2 ), and formaldehyde (CH 2 O).

Fig. 19. Models of molecules with 12-electron shells.
All other alkenes, dienes, and trienes can be considered alkanes containing one, two, or three ethylene groups.
Hydrocarbons belonging to alkynes (C n H 2n-2 ) contain a pair of carbon atoms joined by an elongated 10-electron shell. For each carbon atom there are four electrons, therefore, the missing positions in acetylene are built up by two hydrogen atoms, and in the remaining alkynes these hydrogens are replaced by one or two “hole” bonds with the electron shells of neighboring atoms.

Fig. 20. Models of the electron shells of the simplest alkynes
Thus, for all the main types of hydrocarbons — alkanes, arenes, alkenes, and alkynes — it is possible to construct models of the external electron shells that satisfy all the canons of Kenneth Snelson's theory. Moreover, such shells can serve as samples for molecular prototyping of compounds containing not only carbon atoms. Illustrative examples are the 12-electron shells described above for analogs of ethylene — diimide, oxygen, and formaldehyde. By analogy with them, it would be interesting to consider the Snelson shells of more complex molecules containing 10-electron structures of the acetylene type.
Molecules with ten-electron shells
The spherical shell, built of ten electronic rings, is able to stretch in different directions. Best of all - along the axis of symmetry passing through a pair of electrons located at the "poles". For chemically unstable acetylene (C 2 H 2 ), this axis passes through hydrogen atoms. Molecular nitrogen (N 2 ), which is characterized by chemical resistance , has no hydrogen atoms, and the elongated electron shell is characterized by increased strength. A similar Snelson 10-electron shell can also be constructed for some other simple molecules.

Fig. 21. Models of 10-electron shells of the simplest molecules
More complex electronic shells containing inserts of 10-electron elements can have molecules of urea, acetone, acetamide, carbonic and acetic acids, as well as guanidine. A characteristic feature of all molecules of this type is their magnetic isomerism and the presence of interatomic bonds with electronic inserts ("electronic" bonds).

Fig. 22. Models of shells of molecules with 10-electron central groups.
Especially often in organic compounds there is a 10-electron group of carbon monoxide (CO). Some heterocyclic compounds contain two, three or even four such groups.

Fig. 23. Examples of heterocycles with 10-electron CO groups
A characteristic feature of the electron shells of such molecules is the presence of lonsdaleite type atomic bonds (with insertions of interatomic electrons). Similar "electronic" bonds can be present in many other molecules. For example, for polyiodides (I 3 - , I 5 - , I 7 - , I 9 - and others), crystallizing from solutions containing iodides (I - ) and iodine (I 2 ) / 5 /.

Fig. 24. The model of the electron shell of anion I 3 - with interatomic bonds of the Lonsdaleite type
It would be very interesting to analyze the structure of the electron shells of numerous halogen compounds, but only for a limited circle of chemists. Therefore, it is better to verify the correctness of the theory proposed by Snelson by constructing the electron shells of more well-known molecules - proteins, DNA, etc.
Biomolecules
The main structural element of all protein molecules is the peptide bond. The coincidence of its known parameters with the parameters of the ring-shaped electron shell can serve as a good proof of the correctness of Snelson's theory. And the discrepancy is a refutation.

Fig. 25. Peptide bond. The
grommet displays only the electron shell, which does not allow precise determination of the angles between the centers of atoms. Nevertheless, their general arrangement is consistent with the schemes from the textbooks / 6 /. For example, the layout clearly shows the planarity of the three bonds of the peptide nitrogen atom, which in most of its compounds are pyramidal. Such planarity can be explained by the presence of an interatomic electron between the 10-electron shell of CO and the octagonal shell of the nitrogen atom. This electron is adjacent to the NC (“hole”) bond unfilled by the electron (denoted by a transparent grommet), and in this case the opposite face of the shell of the nitrogen atom becomes the most stable position for the protonated electron (hydrogen atom).
The decrease in the length of the peptide bond (CO) -N (1.32 Å) compared with the length of the single bond CN (1.47 Å) can also be explained by the presence of an interatomic (“lonsdaleite”) electron in it. Thus, in the layout of the electronic shell of the peptide bond constructed in accordance with the Snelson theory, there are no fundamental discrepancies with generally accepted ideas about its structure.
The construction of ring-shaped electron shells is apparently also applicable for modeling the spatial structure of proteins, but for large molecules it is more convenient to use not cringles and similar models, but computer 3D modeling. Attempts to such modeling are discussed in detail in the recently published monograph / 7 /.
Another proof of the correctness of Snelson's theory can be built on the layout of the electron shells of the four bases of DNA. And to demonstrate the presence of hydrogen bonds in pairs of complementary bases of AT and GC.
When describing the electron shells of these nitrogenous bases, it is desirable to adhere to the generally accepted numbering of the pyrimidine (C and T) and purine (A and G) nitrogen base atoms shown in the figure.

Fig. 26. Nitrogen bases of DNA
A characteristic feature of the structure of the bases C, T, G, and A, as well as their pairs in the DNA, is planarity. It follows that at least some of the bonds of nitrogen atoms in these bases can be either identical or similar to the planar peptide bond CO-N.
The planarity of bonds is also characteristic of the ten-electron pairs -CH = CH- and -CH = N- that form benzene, which are part of such benzene analogues as pyrimidine and pyrazine. There are two ten-electron pairs of benzene type atoms in cytosine (C 5 -C 6 , N 3 -C 4 ), in thymine one (C 5 -C 6 ), in adenine four (C 4 -C 5 , N 1 -C 6 , C 2 -N 3 , N 7 -C 8 ) and guanine have three (C 4 -C 5 , C 2 -N 3 , N 7 -C8 ).
It is easy to get confused in the various bonds of purine and pyrimidine heterocycles, so it is better to consider them on the models of electronic shells.

Fig. 27. Models of electronic shells of nitrogenous bases (the oxygen atom of deoxyribose is denoted by an eight-electron shell of transparent grommets).
At least five types of interatomic bonds are found in ring-shaped electronic shells of nitrogenous bases:
• electronic (lonsdaleite type, with an atomic electron insert);
• hole (without electronic insert);
• benzene (bonds -C = C- and -N = C- with pairs of five-electron shells);
• ten-electron (СО);
• fan (four electronic rings linked at one point).
For example, cytosine has four electronic bonds (N 1 -C 2 , C 4 -C 5 , C 4 - (NH2 ) and C 6 -N 1 ), one hole (N 1 -dRib), two benzene (N 3 -C 4 , C 5 -C 6 ), one ten-electron (C 2 O) and one fan (C 2 -N 3 ). Thymine has four electronic bonds (N 1 -C 2 , C 2 -N 3 , N 3 -C 4 and C 6 -N 1 ), two hole (C 5 - (CH 3 )) and N 1 -dRib), one benzene (C 5 -C 6), two ten-electron (C 2 O, C 4 O) and one fan (C 4 -C 5 ). All this, of course, is interesting, but it would be more interesting to look at the presence of hydrogen bonds in complementary pairs of nitrogenous bases.

Fig. 28. Nitrogen base complementarity
On grommet models of Snelson electron shells, two hydrogen bonds in the AT pair and three in the GC are clearly visible. This is unlikely to be a mere coincidence. And for those who understand the intricacies of DNA structure, this can serve as an indisputable proof of the correctness of Kenneth Snelson's theory. The only stumbling block for them will be the magnetic isomerism of the electron shells of all biomolecules, which does not fit into modern ideas about their structure.
Magnetic isomers of biomolecules can hardly be distinguished by any physical methods, but their organoleptic properties should differ greatly, which can be demonstrated by the example of magnetic isomers of ethanol (C 2 H 5 OH).

Fig. 29. Magnetic isomers of ethanol.
As you know, even the highest purity ethanol, diluted to a standard concentration of 40%, is practically impossible to drink without a snack and in an uncooled form. But fresh moonshine of the same concentration is drunk even warm. An appetizer in this case will not be superfluous, but if you drink a little, you can do without it. Any chemist with basic equipment is capable of checking this. And not even a chemist, if he prefers to rely on his own experience and has a moonshine.
Snelson's theory allows one to explain this fact by preserving the magnetic isomerism of ethanol in fresh moonshine and racemizing its molecules in purified alcohol, but quantum mechanics is powerless here. But do not dissuade connoisseurs of quantum mechanics with such examples. They don’t understand.
Conclusion
The theory of the structure of the electron shells of atoms and molecules, proposed by Kenneth Snelson, is unlikely in the near future to compete with quantum-mechanical concepts based on a harmonious system of postulates. The main postulate of this system - the Heisenberg uncertainty principle - could not be refuted even by Einstein, therefore, when meeting with experts in quantum mechanics, do not try to argue with them. And try not to smile. It annoys others.
LIST OF REFERENCES
1. Kenneth Snelson; Art and Ideas / In association with Marlborough gallery, NY, 2013, NY, 174 R. http://kennethsnelson.net/KennethSnelson_Art_And_Ideas.pdf
2. Kozhevnikov D.N. The creation and use of a complex of models of atoms and molecules to study the structure of matter in a chemistry course in high school // Diss. for the competition degrees of cand. ped Sciences, 2004. - 171 p.
3. Haimann RB, Evsyukov S.E. Allotropy of carbon // Nature. 2003. - No. 8. - p. 66-72.
4. Sladkov A. M., Kudryavtsev Yu. P. Diamond, graphite, carbine - allotropic forms of carbon // Nature. - 1969. - No. 5. - p. 37-44.
5. Ivanov D.M., Ivanov M.G. Chemistry of halogens // Textbook. - 2014. - Publishing House of the Ural University. - 82 p.
6. Ovchinnikov Yu.A. Bioorganic chemistry // 1987. - M .: Publishing house "Education", 814 p.
7. Sokolik VV, Kushelev A.Yu. The geometry of a living nanoworld. Protein picotechnology / Lambert Academic Publishing, 2016 .-- 292 p.
PS: A variant of the article in PDF format can be found here .
