Portrait photography: bokeh, focal length, aperture and distance
At the bottom there is an update.
Greetings, photo geeks! Portrait photography, in a good way, is an art. And art is a subjective thing.
But for photography we use technical devices, which means that they are inevitably “fettered” by the laws to which this technique obeys. And I would like to talk about them, because the myths here are full of ... Who wants to immediately read something new about blurring, can immediately scroll much lower

To begin with, I want to remember that we are often limited by some “genre conventions”. There are certain “classic” frame layouts. For example, a chest-to-face portrait, where the frame fits a region of space of about 75 cm diagonally. Or a portrait “head and shoulders”, where about 50 cm are obtained diagonally. These two options are the most common “patterns” of photographs. In the future, it will be about frames with a diagonal of 50 and 75 cm.
Now a little geometry ... Strong perspective distortions of the face are considered aesthetically unattractive, "ugly". Because of this, taking portraits from a distance of less than 1 m is considered incorrect. Of course, what is considered ugliness and what is “the artist’s vision” is a moot point, but still, many special portrait lenses simply cannot be focused much closer than this distance. The professional portrait lens Canon EF 85mm f / 1.2L USM, for example, focuses no closer than 95 cm.
But the complete absence of perspective distortion is also considered ... Distortion! Like, “the face looks too flat”, because with the naked eye from a long distance the face is already poorly visible, so we are not used to seeing a large face completely “without perspective”. Because of this, shooting portraits from a distance of more than 3 m is also not recommended.
It is considered optimal to take people from a distance of about 1.5-2.0 m.
What focal length should the lens have to capture 75 cm diagonally from a distance of 1.5-2.0 m? If we have a classic 36x24 mm film frame or a “full frame” matrix, then 80-100 mm.
What focal length is needed to capture 50 cm diagonally from a distance of 1.5-2.0 m? 110-145 mm.
And what are our classic focal lengths for portrait lenses? 85 and 135 mm ... I think now it should be quite obvious why these numbers were chosen. It’s just that these focal lengths provide shooting of “patterned” frames in composition from the optimal distance.
Often people misunderstand the meaning of the phrase that “these lenses provide minimal distortion to the face,” believing that the focal length itself affects the distortion. But no, this is a mistake, distortions are determined by distance. Of course, the lenses themselves introduce distortion, distortion. But the opinion that it is minimal in 85 and 135 mm lenses is absolutely untrue. So, for example, the Canon EF 35mm f / 1.4L II USM wide-angle lens has a barrel-shaped (it makes the face “puffier”) distortion of 0.1%. Because it is not suitable for portraits? .. No, the above-mentioned portrait 85-mm Canon is also barrel-shaped, and even 0.2%!
So choosing exactly the focal length of the lens, you need to look at what viewing angle it has on the matrix of your camera. On the Nikon 1, with its scanty matrix, the 35 mm lens will be a great “cock”, which, if properly designed, will not create any face distortion for you. All the conversations "crop factor does not matter, the lens as it was, it is wide-angle" is just an indicator of people's misunderstanding of optics and geometry.
Now we have to scroll to here.
Now let's move on to another interesting aspect of shooting portraits - bokeh ...

There are many holivars on the subject of “Wow! What a gorgeous background blur! This is great! ”VS“ Only stupid novices shoot on the open aperture, a professional chooses a beautiful background. ” We won’t get into them, we just take it for granted that there is a significant layer of people who want to see a “blurry background” in the portraits, and try to help them choose the right lens.
It is well known that the smaller the number of apertures, the more the background will be blurred. f / 1.4 is better than f / 2.0. And f / 1.2 is generally fine.
It is also known that the larger the focal length (but do not forget about what was said in the first part of the article!), The more the background is blurred.
But what will blur the background stronger, 50 mm f / 1.4 or 85 mm f / 2.0 ?! And if they are also on cameras with different matrix sizes? ..
Actually, the whole article got out of this question. To take ten different lenses and “drive” them through several cameras with different matrices, shooting different portraits in different conditions - the experiment is interesting, but long and expensive. So I decided to do mathematical modeling ...
The “sphericity” of the “horse in vacuum” in my case was that I considered the lens to be the only one lens that moves back and forth to focus. I simply didn’t have other options, because I wanted to find out how the focal length and aperture in general, and not a specific lens, affect the blurring of the background. But the same focal length with the aperture can be for lenses of completely different designs ... So blurring the background (and even the distance at which it will give the desired diagonal of the frame!) For a particular real lens can be slightly different. So, for example, in the photo above it is clearly visible that a point light source out of focus can be depicted not even as a circle, but as an oval ... But, nevertheless, in most cases the differences between my calculation and the results of a real lens will be insignificant.
What have I actually done? Having written sheet A4 on both sides by transformations of the basic formula of a thin lens, I got a calculation of how far (from the plane of the matrix / film, it is from it that the distances on the lens focusing scale are counted) to place an object to get the desired frame diagonal at a given focal length and the size of the matrix, as well as in what size circle a point source of light located at a given distance behind the subject is scattered (I calculated the distance from the subject exactly, because usually changing the lens of a photographer with m leaves / she comes closer, and does not ask to approach / depart portrayed). I expressed this size as a percentage of the diagonal of the frame so that you can directly compare it for cameras with different matrices.
Next, this exel file was created.. Orange cells are what we set (frame diagonal, matrix sizes, distance from the object to the background), yellow are the main calculation results (distance to assess whether this is focal for such a portrait, and background blur), gray - intermediate calculation results (for example, “defocusing the background” is the distance from the plane in which the background was focused to the plane of the matrix).
I sincerely believed that the results of the calculation would be simple conclusions like “50 mm f / 1.4 erodes the background worse than 85 mm f / 2.0”. But no!
If you take a portrait “on the chest” (75 cm) by installing both lenses on a camera with a 23.5x15.6 mm sensor (the most common APS-C format), then 50 mm f / 1.4 will give a blur of 2.76% and 85 mm f / 2.0 - 2.56%, i.e. 50 mm “won”. But at the same time50 mm f / 1.4 will give a blur of 4.30%, and 85 mm f / 2.0 - 4.91%, i.e. “Ahead” 85 mm!
How so? .. Very simple: the first pair of numbers is given for the case when the background is only a couple of meters behind the back of a person (which usually happens indoors), and the second when the background is already 20 meters (which happens regularly in nature).
Those. choosing which lens to take to blur the background as much as possible, you need to be guided not only by their focal lengths and aperture sizes, but also by the distance from the portrait to the background .
And how to be guided - download the file and "play." I will give here only a few very "truncated" tables.
Format:
focal length (focus distance): aperture number (1.2, 1.4, etc.) - blur (percent)
Full frame (36x24 mm), 50 cm diagonal, to the background 2 m
85 mm (1.16 m): 1.2 - 8.75; 1.4 - 7.50; 1.8 - 5.83
135 mm (1.84 m): 2.0 - 6.99; 2.8 - 4.99; 3.5 - 3.99
Full frame (36x24 mm), 50 cm diagonal, to the background 20 m
85 mm (1.16 m): 1.2 - 12.43; 1.4 - 10.65; 1.8 - 8.29
135 mm (1.84 m): 2.0 - 11.53; 2.8-8.23; 3.5 - 6.59
Full frame (36x24 mm), 75 cm diagonal, to the background 2 m
85 mm (1.65 m): 1.2 - 5.14; 1.4 - 4.41; 1.8 - 3.43
135 mm (2.62 m): 2.0 - 3.92; 2.8 - 2.80; 3.5 - 2.24
Full frame (36x24 mm), 75 cm diagonal, to the background 20 m
85 mm (1.65 m): 1.2 - 8.32; 1.4 - 7.13; 1.8 - 5.54
135 mm (2.62 m): 2.0 - 7.62; 2.8 - 5.44; 3.5 - 4.35
APS-C matrix (22.3x14.9 mm, crop 1.61), 50 cm diagonal, to the background 2 m
50 mm (1.03 m): 1.2 - 5.40; 1.4 - 4.63; 1.8 - 3.60
85 mm (1.76 m): 1.2 - 7.51; 1.4 - 6.43; 1.8 - 5.00
APS-C matrix (22.3 x 14.9 mm, crop 1.61), 50 cm diagonal, to the background 20 m
50 mm (1.03 m): 1.2 - 7.56; 1.4 - 6.48; 1.8 - 5.04
85 mm (1.76 m): 1.2 - 12.46; 1.4 - 10.68; 1.8 - 8.31
APS-C matrix (22.3x14.9 mm, crop 1.61), 75 cm diagonal, to the background 2 m
50 mm (1.50 m): 1.2 - 3.16; 1.4 - 2.71; 1.8 - 2.10
85 mm (2.55 m): 1.2 - 4.17; 1.4 - 3.57; 1.8 - 2.78
APS-C matrix (22.3 x 14.9 mm, crop 1.61), 75 cm diagonal, to the background 20 m
50 mm (1.50 m): 1.2 - 5.01; 1.4 - 4.30; 1.8 - 3.24
85 mm (2.55 m): 1.2 - 8.15; 1.4 - 6.99; 1.8 - 5.43
I hope this helps someone a little with choosing a lens for portrait photography :)
UPDATE:
I updated the Exel file .
Now, for a number of lenses, he is plotting the dependence of the background blur on the distance to it. Here's one: The
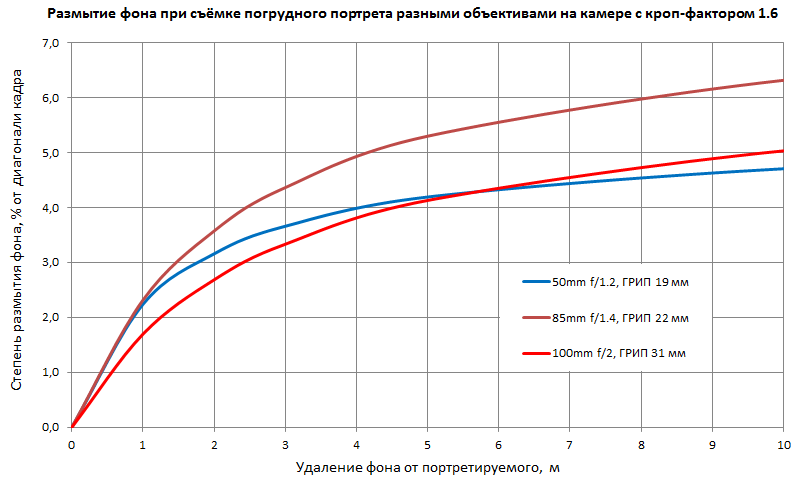
graph clearly demonstrates the capabilities of various lenses at different distances to the background.
Well, a comparison of the theoretical model with practice ...
Canon EOS M5, 22.3x14.9 mm image sensor, Canon EF 50mm f / 1.8 STM lens, focusing distance 1.5 m, 3.5 m from the camera (2 m behind focusing plane) located LED.
The LED image on the photo turned out to be approximately (it is not perfectly round and has not perfectly clear edges, so there is an error of ± 2-3 pixels) of 150 pixels.
The resolution of the matrix is 6000x4000 pixels, which gives 7211 conditional pixels on the diagonal of the frame.
150/7211 = 2.08% The
mathematical model predicted 2.10%. Within the limits of measurement error, the result of the experiment coincided with the predictions of the theory.
Greetings, photo geeks! Portrait photography, in a good way, is an art. And art is a subjective thing.
But for photography we use technical devices, which means that they are inevitably “fettered” by the laws to which this technique obeys. And I would like to talk about them, because the myths here are full of ... Who wants to immediately read something new about blurring, can immediately scroll much lower

To begin with, I want to remember that we are often limited by some “genre conventions”. There are certain “classic” frame layouts. For example, a chest-to-face portrait, where the frame fits a region of space of about 75 cm diagonally. Or a portrait “head and shoulders”, where about 50 cm are obtained diagonally. These two options are the most common “patterns” of photographs. In the future, it will be about frames with a diagonal of 50 and 75 cm.
Now a little geometry ... Strong perspective distortions of the face are considered aesthetically unattractive, "ugly". Because of this, taking portraits from a distance of less than 1 m is considered incorrect. Of course, what is considered ugliness and what is “the artist’s vision” is a moot point, but still, many special portrait lenses simply cannot be focused much closer than this distance. The professional portrait lens Canon EF 85mm f / 1.2L USM, for example, focuses no closer than 95 cm.
But the complete absence of perspective distortion is also considered ... Distortion! Like, “the face looks too flat”, because with the naked eye from a long distance the face is already poorly visible, so we are not used to seeing a large face completely “without perspective”. Because of this, shooting portraits from a distance of more than 3 m is also not recommended.
It is considered optimal to take people from a distance of about 1.5-2.0 m.
What focal length should the lens have to capture 75 cm diagonally from a distance of 1.5-2.0 m? If we have a classic 36x24 mm film frame or a “full frame” matrix, then 80-100 mm.
What focal length is needed to capture 50 cm diagonally from a distance of 1.5-2.0 m? 110-145 mm.
And what are our classic focal lengths for portrait lenses? 85 and 135 mm ... I think now it should be quite obvious why these numbers were chosen. It’s just that these focal lengths provide shooting of “patterned” frames in composition from the optimal distance.
Often people misunderstand the meaning of the phrase that “these lenses provide minimal distortion to the face,” believing that the focal length itself affects the distortion. But no, this is a mistake, distortions are determined by distance. Of course, the lenses themselves introduce distortion, distortion. But the opinion that it is minimal in 85 and 135 mm lenses is absolutely untrue. So, for example, the Canon EF 35mm f / 1.4L II USM wide-angle lens has a barrel-shaped (it makes the face “puffier”) distortion of 0.1%. Because it is not suitable for portraits? .. No, the above-mentioned portrait 85-mm Canon is also barrel-shaped, and even 0.2%!
So choosing exactly the focal length of the lens, you need to look at what viewing angle it has on the matrix of your camera. On the Nikon 1, with its scanty matrix, the 35 mm lens will be a great “cock”, which, if properly designed, will not create any face distortion for you. All the conversations "crop factor does not matter, the lens as it was, it is wide-angle" is just an indicator of people's misunderstanding of optics and geometry.
Now we have to scroll to here.
Now let's move on to another interesting aspect of shooting portraits - bokeh ...

There are many holivars on the subject of “Wow! What a gorgeous background blur! This is great! ”VS“ Only stupid novices shoot on the open aperture, a professional chooses a beautiful background. ” We won’t get into them, we just take it for granted that there is a significant layer of people who want to see a “blurry background” in the portraits, and try to help them choose the right lens.
It is well known that the smaller the number of apertures, the more the background will be blurred. f / 1.4 is better than f / 2.0. And f / 1.2 is generally fine.
It is also known that the larger the focal length (but do not forget about what was said in the first part of the article!), The more the background is blurred.
But what will blur the background stronger, 50 mm f / 1.4 or 85 mm f / 2.0 ?! And if they are also on cameras with different matrix sizes? ..
Actually, the whole article got out of this question. To take ten different lenses and “drive” them through several cameras with different matrices, shooting different portraits in different conditions - the experiment is interesting, but long and expensive. So I decided to do mathematical modeling ...
The “sphericity” of the “horse in vacuum” in my case was that I considered the lens to be the only one lens that moves back and forth to focus. I simply didn’t have other options, because I wanted to find out how the focal length and aperture in general, and not a specific lens, affect the blurring of the background. But the same focal length with the aperture can be for lenses of completely different designs ... So blurring the background (and even the distance at which it will give the desired diagonal of the frame!) For a particular real lens can be slightly different. So, for example, in the photo above it is clearly visible that a point light source out of focus can be depicted not even as a circle, but as an oval ... But, nevertheless, in most cases the differences between my calculation and the results of a real lens will be insignificant.
What have I actually done? Having written sheet A4 on both sides by transformations of the basic formula of a thin lens, I got a calculation of how far (from the plane of the matrix / film, it is from it that the distances on the lens focusing scale are counted) to place an object to get the desired frame diagonal at a given focal length and the size of the matrix, as well as in what size circle a point source of light located at a given distance behind the subject is scattered (I calculated the distance from the subject exactly, because usually changing the lens of a photographer with m leaves / she comes closer, and does not ask to approach / depart portrayed). I expressed this size as a percentage of the diagonal of the frame so that you can directly compare it for cameras with different matrices.
Next, this exel file was created.. Orange cells are what we set (frame diagonal, matrix sizes, distance from the object to the background), yellow are the main calculation results (distance to assess whether this is focal for such a portrait, and background blur), gray - intermediate calculation results (for example, “defocusing the background” is the distance from the plane in which the background was focused to the plane of the matrix).
I sincerely believed that the results of the calculation would be simple conclusions like “50 mm f / 1.4 erodes the background worse than 85 mm f / 2.0”. But no!
If you take a portrait “on the chest” (75 cm) by installing both lenses on a camera with a 23.5x15.6 mm sensor (the most common APS-C format), then 50 mm f / 1.4 will give a blur of 2.76% and 85 mm f / 2.0 - 2.56%, i.e. 50 mm “won”. But at the same time50 mm f / 1.4 will give a blur of 4.30%, and 85 mm f / 2.0 - 4.91%, i.e. “Ahead” 85 mm!
How so? .. Very simple: the first pair of numbers is given for the case when the background is only a couple of meters behind the back of a person (which usually happens indoors), and the second when the background is already 20 meters (which happens regularly in nature).
Those. choosing which lens to take to blur the background as much as possible, you need to be guided not only by their focal lengths and aperture sizes, but also by the distance from the portrait to the background .
And how to be guided - download the file and "play." I will give here only a few very "truncated" tables.
Format:
focal length (focus distance): aperture number (1.2, 1.4, etc.) - blur (percent)
Full frame (36x24 mm), 50 cm diagonal, to the background 2 m
85 mm (1.16 m): 1.2 - 8.75; 1.4 - 7.50; 1.8 - 5.83
135 mm (1.84 m): 2.0 - 6.99; 2.8 - 4.99; 3.5 - 3.99
Full frame (36x24 mm), 50 cm diagonal, to the background 20 m
85 mm (1.16 m): 1.2 - 12.43; 1.4 - 10.65; 1.8 - 8.29
135 mm (1.84 m): 2.0 - 11.53; 2.8-8.23; 3.5 - 6.59
Full frame (36x24 mm), 75 cm diagonal, to the background 2 m
85 mm (1.65 m): 1.2 - 5.14; 1.4 - 4.41; 1.8 - 3.43
135 mm (2.62 m): 2.0 - 3.92; 2.8 - 2.80; 3.5 - 2.24
Full frame (36x24 mm), 75 cm diagonal, to the background 20 m
85 mm (1.65 m): 1.2 - 8.32; 1.4 - 7.13; 1.8 - 5.54
135 mm (2.62 m): 2.0 - 7.62; 2.8 - 5.44; 3.5 - 4.35
APS-C matrix (22.3x14.9 mm, crop 1.61), 50 cm diagonal, to the background 2 m
50 mm (1.03 m): 1.2 - 5.40; 1.4 - 4.63; 1.8 - 3.60
85 mm (1.76 m): 1.2 - 7.51; 1.4 - 6.43; 1.8 - 5.00
APS-C matrix (22.3 x 14.9 mm, crop 1.61), 50 cm diagonal, to the background 20 m
50 mm (1.03 m): 1.2 - 7.56; 1.4 - 6.48; 1.8 - 5.04
85 mm (1.76 m): 1.2 - 12.46; 1.4 - 10.68; 1.8 - 8.31
APS-C matrix (22.3x14.9 mm, crop 1.61), 75 cm diagonal, to the background 2 m
50 mm (1.50 m): 1.2 - 3.16; 1.4 - 2.71; 1.8 - 2.10
85 mm (2.55 m): 1.2 - 4.17; 1.4 - 3.57; 1.8 - 2.78
APS-C matrix (22.3 x 14.9 mm, crop 1.61), 75 cm diagonal, to the background 20 m
50 mm (1.50 m): 1.2 - 5.01; 1.4 - 4.30; 1.8 - 3.24
85 mm (2.55 m): 1.2 - 8.15; 1.4 - 6.99; 1.8 - 5.43
I hope this helps someone a little with choosing a lens for portrait photography :)
UPDATE:
I updated the Exel file .
Now, for a number of lenses, he is plotting the dependence of the background blur on the distance to it. Here's one: The

graph clearly demonstrates the capabilities of various lenses at different distances to the background.
Well, a comparison of the theoretical model with practice ...
Canon EOS M5, 22.3x14.9 mm image sensor, Canon EF 50mm f / 1.8 STM lens, focusing distance 1.5 m, 3.5 m from the camera (2 m behind focusing plane) located LED.
The LED image on the photo turned out to be approximately (it is not perfectly round and has not perfectly clear edges, so there is an error of ± 2-3 pixels) of 150 pixels.
The resolution of the matrix is 6000x4000 pixels, which gives 7211 conditional pixels on the diagonal of the frame.
150/7211 = 2.08% The
mathematical model predicted 2.10%. Within the limits of measurement error, the result of the experiment coincided with the predictions of the theory.
