Proof-of-Proof-of-Work on the fingers. Towards a smart blockchain
Blockchain protocols should provide consensus among the nodes of a decentralized system. Perhaps the most well-known consensus algorithm can be considered the “slowed down, but reliable, because the slowed down" Proof-of-Work algorithm: each node, having a set of new transactions, iterates over a certain number of nonce, which is a block field. A block is considered valid if all transactions inside it are valid and the hash function of the block header has some generally accepted feature (for example, the number of zeros at the beginning, as in Bitcoin):
As you know, blockchain is a chain of blocks. It is a chain because each block contains an id (usually a hash from the header) of the previous block. For subsequent reasoning, the blockchain in a simplified form can be represented as follows:

In the process of synchronizing the nodes with other nodes, it needs to validate all the blocks that the neighbors sent to it - check the hashes and transactions of all new blocks, and in the case of the first connection, to the very first block ( genesis -block). It is easy to assume that this is a rather lengthy and costly process ...
There is an option to request the last few blocks from neighboring nodes and, having trusted, accept them as valid. But this option does not meet the security spirit in an “environment where no one trusts anyone”
The hash function of the block header is its id. As mentioned earlier, in the Bitcoin network, as in many other networks, the feature that determines the validity of a block is the number of zeros at the beginning of the id record. This is the well-known and common number of zeros for all miners, called the complexity of mining T (mining target). A valid hash with T zeros at the beginning can have more zeros at the beginning than T. More specifically, half the blocks will only have T zeros at the beginning; half of the blocks will have T + 1 zero at the beginning; a quarter of blocks T + 2 zeros, etc. For example, a set of valid blocks for T = 5 might look like this:
The number of zeros exceeding T in the id of the block is called the level µ, and blocks with the level µ will be called µ - superblocks. If the block is a µ-superblock, then it is also a
(µ -1) -block. Thus, while not changing anything, but only using the entered parameter µ, we can represent the chain of blocks in the following µ-level form:
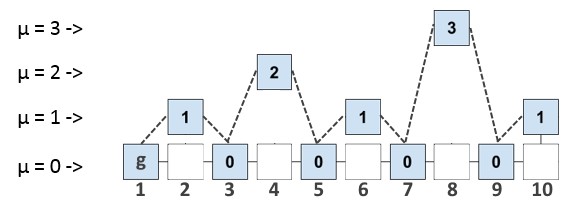
Blocks are numbered for ease of description, the numbering does not carry a meaning.
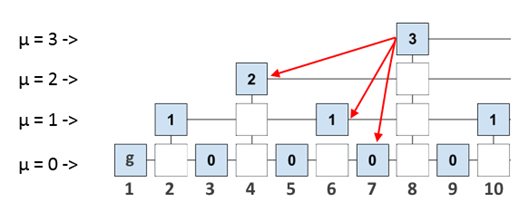
Now let's think about how we can use it. If we write in the header of each block not only the id of the previous block, but also the id of all the last blocks at each level, then we allow each block to refer to more “ancient” blocks than the previous one. The set of all the last blocks at each level will be called interlink (multiple link). For example, Interlink for block 8 looks like this:
What does this give us? Let's say we connected a new node and now we want to synchronize it safely. As we have already said, in order to fully validate a new block, the node needs to “step through” to genesis - a block throughout the blockchain. However, if we have links to some “supporting” blocks in the validated block, we can “walk” to the genesis block, requesting from the other nodes not the entire blockchain, but only some proof, which will contain a short route to first block. The route itself will be a valid subchain of the blockchain itself, since the blocks of the subchain sequentially refer to each other.
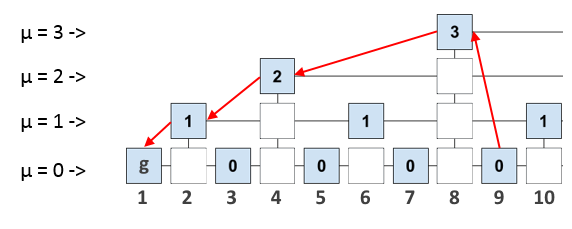
A proof is a collection of titles from several previous blocks. Strictly speaking, the proof contains not only a “short route”, but also a few more headings of other blocks. This is done to verify the evidence using the specified security parameters m, k, etc. (a detailed description is given in the original article, link at the end).
A node that does not store the entire blockchain, but only asks for proof from full-nodes that store the entire history, is called PoPoW - a node. Theoretically, such a node can be deployed on a low-power computer, smartphone.
The PoPoW protocol operation algorithm is as follows:
1. The PoPoW node asks for proof for the block from the full node.
2. Full - a node (proover) forms a proof and sends it.
3. The PoPoW node (verifier) checks the proof, compares it with the proofs of other nodes and draws a conclusion about the validity of the block.
It is also worth noting that the complexity of creating PoPoW proofs is not inferior to the complexity of creating a complete chain of valid headers (the hash function of the header contains Interlink, so the fraudulent node would have to “fake” the blocks taking into account the µ-level hierarchy). Therefore, using evidence to validate a PoPoW block does not entail a loss of security.
The NiPoPoW Algorithm - Non-Interactive Proof-of-Proof-of-Work - includes advanced evidence generation and verification, and is resistant to some of the attacks that PoPoW is prone to. A link to the original article from the authors is also at the end.
Using these algorithms, two topical problems are solved: effective transaction verification and effective evidence for sidechains.
In the first case, this algorithm allows you to connect “light” nodes to the network, which can quickly synchronize with the network.
In the second case, the algorithm allows you to store and refer to events that occurred on other blockchain networks, which is useful for clients and wallets working with several blockchains. The PoPoW proof is short enough to fit into a transaction. For example, you can write smart contracts in blockchain A, which rely on some events in blockchain B.
This review was compiled with a fresh mind after participating in the Unblock Hackathon hackathon, where one of the tasks was to implement this protocol. The authors of the task were partners of the hackathon from the Ergo platform , inside which this algorithm is used.
The text is based on original articles by
PoPoW: Proofs of Proofs of Work with Sublinear Complexity. Aggelos Kiayias, Nikolaos Lamprou, and Aikaterini-Panagiota Stouka
NiPoPoW: Non-Interactive Proofs of Proof-of-Work. Aggelos Kiayias, Andrew Miller and Dionysis Zindros
Hash( Block{transaction,nonce,…} ) = 000001001...As you know, blockchain is a chain of blocks. It is a chain because each block contains an id (usually a hash from the header) of the previous block. For subsequent reasoning, the blockchain in a simplified form can be represented as follows:

In the process of synchronizing the nodes with other nodes, it needs to validate all the blocks that the neighbors sent to it - check the hashes and transactions of all new blocks, and in the case of the first connection, to the very first block ( genesis -block). It is easy to assume that this is a rather lengthy and costly process ...
There is an option to request the last few blocks from neighboring nodes and, having trusted, accept them as valid. But this option does not meet the security spirit in an “environment where no one trusts anyone”
PoPoW nodes.
The hash function of the block header is its id. As mentioned earlier, in the Bitcoin network, as in many other networks, the feature that determines the validity of a block is the number of zeros at the beginning of the id record. This is the well-known and common number of zeros for all miners, called the complexity of mining T (mining target). A valid hash with T zeros at the beginning can have more zeros at the beginning than T. More specifically, half the blocks will only have T zeros at the beginning; half of the blocks will have T + 1 zero at the beginning; a quarter of blocks T + 2 zeros, etc. For example, a set of valid blocks for T = 5 might look like this:
000000101… (6 нулей)
000001110… (5 нулей)
000001111… (5 нулей)
000000010… (7 нулей)
000000101… (6 нулей)
000001110… (5 нулей)
000001111… (5 нулей)
The number of zeros exceeding T in the id of the block is called the level µ, and blocks with the level µ will be called µ - superblocks. If the block is a µ-superblock, then it is also a
(µ -1) -block. Thus, while not changing anything, but only using the entered parameter µ, we can represent the chain of blocks in the following µ-level form:

Blocks are numbered for ease of description, the numbering does not carry a meaning.
Now let's think about how we can use it. If we write in the header of each block not only the id of the previous block, but also the id of all the last blocks at each level, then we allow each block to refer to more “ancient” blocks than the previous one. The set of all the last blocks at each level will be called interlink (multiple link). For example, Interlink for block 8 looks like this:

What does this give us? Let's say we connected a new node and now we want to synchronize it safely. As we have already said, in order to fully validate a new block, the node needs to “step through” to genesis - a block throughout the blockchain. However, if we have links to some “supporting” blocks in the validated block, we can “walk” to the genesis block, requesting from the other nodes not the entire blockchain, but only some proof, which will contain a short route to first block. The route itself will be a valid subchain of the blockchain itself, since the blocks of the subchain sequentially refer to each other.

A proof is a collection of titles from several previous blocks. Strictly speaking, the proof contains not only a “short route”, but also a few more headings of other blocks. This is done to verify the evidence using the specified security parameters m, k, etc. (a detailed description is given in the original article, link at the end).
A node that does not store the entire blockchain, but only asks for proof from full-nodes that store the entire history, is called PoPoW - a node. Theoretically, such a node can be deployed on a low-power computer, smartphone.
The PoPoW protocol operation algorithm is as follows:
1. The PoPoW node asks for proof for the block from the full node.
2. Full - a node (proover) forms a proof and sends it.
3. The PoPoW node (verifier) checks the proof, compares it with the proofs of other nodes and draws a conclusion about the validity of the block.
It is also worth noting that the complexity of creating PoPoW proofs is not inferior to the complexity of creating a complete chain of valid headers (the hash function of the header contains Interlink, so the fraudulent node would have to “fake” the blocks taking into account the µ-level hierarchy). Therefore, using evidence to validate a PoPoW block does not entail a loss of security.
NiPoWPoW - algorithm
The NiPoPoW Algorithm - Non-Interactive Proof-of-Proof-of-Work - includes advanced evidence generation and verification, and is resistant to some of the attacks that PoPoW is prone to. A link to the original article from the authors is also at the end.
What is all this for?
Using these algorithms, two topical problems are solved: effective transaction verification and effective evidence for sidechains.
In the first case, this algorithm allows you to connect “light” nodes to the network, which can quickly synchronize with the network.
In the second case, the algorithm allows you to store and refer to events that occurred on other blockchain networks, which is useful for clients and wallets working with several blockchains. The PoPoW proof is short enough to fit into a transaction. For example, you can write smart contracts in blockchain A, which rely on some events in blockchain B.
This review was compiled with a fresh mind after participating in the Unblock Hackathon hackathon, where one of the tasks was to implement this protocol. The authors of the task were partners of the hackathon from the Ergo platform , inside which this algorithm is used.
The text is based on original articles by
PoPoW: Proofs of Proofs of Work with Sublinear Complexity. Aggelos Kiayias, Nikolaos Lamprou, and Aikaterini-Panagiota Stouka
NiPoPoW: Non-Interactive Proofs of Proof-of-Work. Aggelos Kiayias, Andrew Miller and Dionysis Zindros
