Advanced lighting

In the lesson on the basics of lighting, we briefly examined the Phong lighting model, which allows us to give a substantial share of realism to our scenes. The Phong model looks pretty good, but it has several flaws that we will focus on in this tutorial.

Blinn Fong Model

The Phong model is a very effective approximation for calculating lighting, but under certain conditions it may lose some of the specular reflection component. This can be seen at low values of gloss force ( shininess ) when the area of specular reflection becomes quite large. The figure below shows what happens when we use a specular gloss power of 1.0 for a flat textured surface:

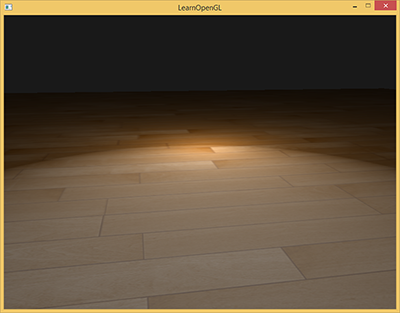
As you can see, the region of specular reflection has a sharply defined boundary. This is because the angle between the viewing vector and the reflection vector should not exceed 90 degrees, otherwise their scalar product becomes negative, which makes the mirror flare component equal to zero. You might think that this is not a big deal, because we shouldn’t get any illumination at angles over 90 degrees, right?

Not really. This applies only to the diffuse component, where an angle above 90 degrees between the normal vector and the direction of the light means that the light source is below the illuminated surface, and therefore, the contribution of diffuse lighting should be zero. However, in the case of the mirror component, we do not measure the angle between the direction of light and the normal, but the angle between the viewing and reflection vectors. Take a look at the following two pictures:

Now the problem is becoming apparent. On the left we see the usual picture of the Fongovsky reflection with θ less than 90 degrees. In the right figure, the angle θ between the directions of view and reflection is greater than 90 degrees, as a result of which the contribution of specular illumination is canceled. This is usually not a cause for concern, since the review vector is often noticeably removed from the reflection vector. But for small values ​​of the specular brightness, the radius of the reflection region becomes quite large, and makes a noticeable contribution to the overall picture. Using the Phong model, we cancel this contribution at angles greater than 90 degrees (as seen in the first image).

In 1977, James F. Blinn introduced the Blinn-Fong lighting model as an addition to the Phong model we have used so far. It is largely similar to the Phong model, but uses a slightly different approach to the calculation of the mirror component, which allows us to solve our problem. Instead of relying on the reflection vector, we use the so-called median vector ( the halfway vector ), which is a unit vector exactly midway between the viewing direction and the direction of light. The closer this vector is to the surface normal, the greater will be the contribution of the mirror component.

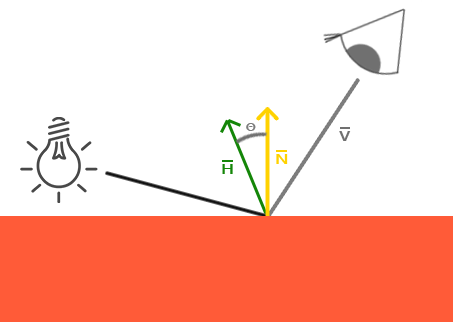
When the direction of the survey completely coincides with the (now imaginary) reflection vector, the median vector coincides with the normal to the surface. Thus, the closer the viewing direction to the direction of reflection, the stronger the specular gloss becomes.

Obviously, regardless of the direction the observer is looking, the angle between the median vector and the normal to the surface will never exceed 90 degrees (unless, of course, the light source is below the surface). Thanks to this, we get slightly different results compared to the Phong reflection, and in general the picture looks more visually plausible, especially at low values ​​of the specular brightness. It was the Blinn-Fong lighting model that was used in the earlier, fixed OpenGL pipeline.

Finding the median vector is easy: you need to add the direction vector of the light with the review vector and normalize the result:

In GLSL, it looks like this:

vec3 lightDir   = normalize(lightPos - FragPos);
vec3 viewDir    = normalize(viewPos - FragPos);
vec3 halfwayDir = normalize(lightDir + viewDir);

Thus, the calculation of the mirror component is reduced to a simple calculation of the scalar product between the normal to the surface and the median vector to obtain the cosine of the angle between them, which we again raise to the power of the specular gloss:

float spec = pow(max(dot(normal, halfwayDir), 0.0), shininess);
vec3 specular = lightColor * spec;

Actually, this is all about the Blinn-Fong model. The only difference between specular reflection in the Blinn-Fong and Fong models is that we now measure the angle between the normal and the median vector instead of the angle between the viewing direction and the reflection vector.

Using the median vector to calculate the specular flare component, we will no longer have problems with the sharp boundary of the specular reflection region that are characteristic of the Phong model. The image below shows the specular reflection region of both methods with a specular brightness of 0.5:

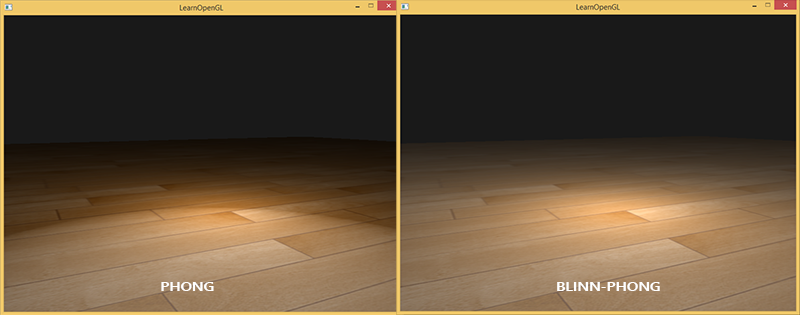
Another small difference between the Phong and Blinn-Fong models is that the angle between the median vector and the normal to the surface is often less than the angle between the viewing and reflection vectors. Therefore, in order to obtain similar Fong models results, the specular gloss value should be slightly higher. It is empirically established that it is somewhere 2-4 times larger than the Phong model.

The following is a comparison of the mirror component between the models with a specular gloss of 8 for the Phong model and 32 for the Blinn-Fong model:

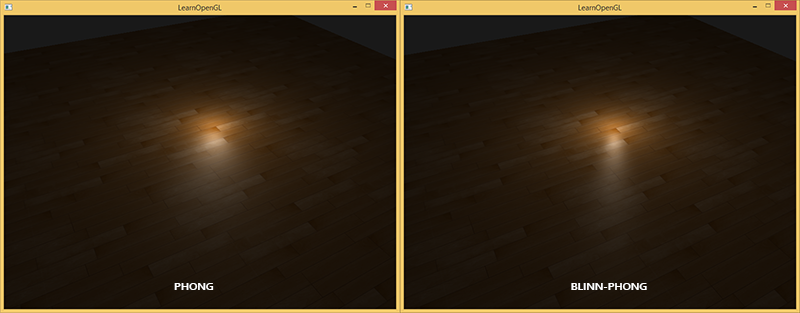
As you can see, the mirror component of Blinn-Fong is sharper. Usually a little adjustment is required to obtain results similar to those obtained previously using the Phong model, but, in general, the Blinn-Fong coverage gives a more plausible picture.

For this demonstration, we used a simple fragment shader that switches between the usual Fong reflection and the Blinn-Fong reflection:

void main()
{
    [...]
    float spec = 0.0;
    if(blinn)
    {
        vec3 halfwayDir = normalize(lightDir + viewDir);  
        spec = pow(max(dot(normal, halfwayDir), 0.0), 16.0);
    }
    else
    {
        vec3 reflectDir = reflect(-lightDir, normal);
        spec = pow(max(dot(viewDir, reflectDir), 0.0), 8.0);
    }
    [...]

The source code for this lesson is here . By pressing b, you can switch from the Fong model to the Blinn-Fong model and vice versa.

Original article .