Ping Pong Algorithm or Criticism of Reverse Polish Notation
This article was written due to outrage that in our universities students are taught a simple analysis of mathematical expressions on the basis of just the Reverse Polish Notation (OPN), which is a frank distortion of normal human logic.
The source of the description of the arrester will be a description from Lafore R .: L29 Data structures and algorithms in Java. Classic Computers Science. 2nd ed. - SPb .: Peter, 2013. - 704 s, recommended as the most popular and adequate on this issue, however, as well as on other commonly used algorithms.
Well, that is, we compare different algorithms with different ideologies.
To visualize the sequence of work on the formula (OPN), the following graph is given on page 158:

Already here you can see the adjustment of the algorithm to the wrong for a person property of sequential reading of symbolic information. For a person, the priority allocation of expression fragments and the construction of a further calculation scheme according to the priorities of these fragments are more characteristic. Therefore, in this case, the scheme will look like this in reality:
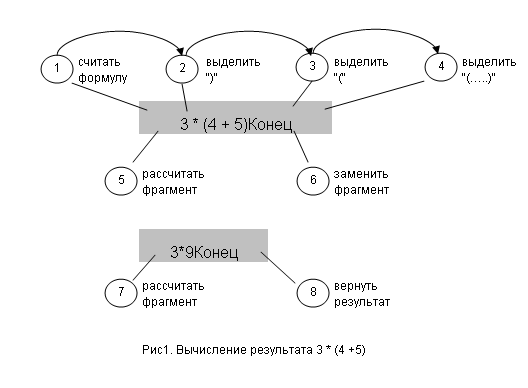
As you can see, an incorrect initial message for character-by-character parsing of an expression not only leads to distortion of infix notation processing, but also significantly complicates the picture of the actual analysis of complex formulas with multiple parentheses. After all, the second scheme (Fig1) is both clearer and significantly shorter than that presented in Fig.4.15 of the analyzed source.
Further, I am forced to quote a rather lengthy quote from the source, in which "the owl is pulled onto the globe."
However, let's look carefully at stage one. Fortunately, the author provides a chic table for this (p. 153):
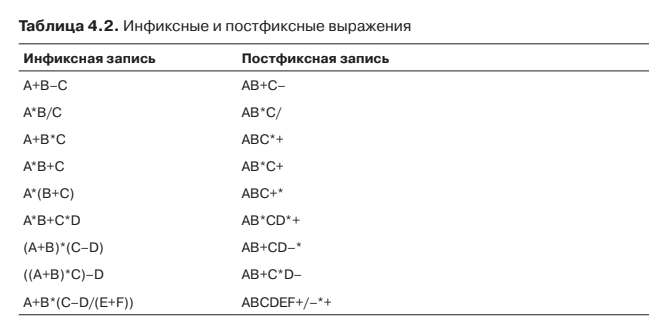
Most of all, I liked the last line. Tell me, for God's sake, how it can be sequentially pulled out of the STACK here and get a sane result. A system of two stacks, separately for operands and separately for operations, will still work, but with one stack ...
But this is not even about that. How many and what sortings should be done to make postfix from an infix (familiar to us) record? Why break the normal human logic of students for the sake of the ancient method? I’m even afraid to imagine how, for example, such a formula would look like: (A + B * C / D) + (EF * ((G / (HJ * (- 1) + I) -L * (MN) -R) + S ). And did you manage to present it at once?
Thus, we can say that the conversion from infix to postfix records already carries unjustifiably high costs for the implementation of complex obscure algorithms for sorting source data. Moreover, the number of returns at this stage will clearly exceed the resources required to process the infix (normal) record. Well, the processing of such a postfix record itself is somehow not limited to primitive pulling in a row from the stack, but requires an appropriate processor and additional resources.
We illustrate the sequence of required operations (OPN) with a small example.

Table 1. The procedure for calculating a fragment of the formula
But this is not all, because if the numbers consist of more than one digit, then you need to put a buffer to assemble the number of individual digits before placing them on the stack or output line.
I have no task to retell the method of calculating the arrester, so those who are particularly interested can read about it in the original source, especially since it is really cool written. Therefore, we turn to the Ping-Pong method (algorithm) announced in the title of the article.
Immediately make a reservation, there are a lot of methods (algorithms) for parsing formulas. You can name the method of recursive descent and the methods of building trees and others. I have not found Ping-Pong on the network, although, so I think, it is used quite often. Why he received such a name will become clear from the illustrations.
So, we proceed to the analysis of the algorithm. Let's start with some definitions for ease of presentation.
Priority - the dominance of one operation or grouping over others. The algorithm uses three priorities: 0 - operations "±"; 1 - operations "* /%"; 2 - grouping with parentheses “()”. Note: functions and work with them are not considered in this article. Functions are just a separate layer that does not affect the priority of operations.
A fragment is a part of a formula that can be passed for a lower level calculation. That is, a fragment is both a part of the formula framed by brackets and containing operations of the 0th and 1st levels, and a trivial fragment containing two operands and the sign of the operation between them.
For the convenience of illustration, we will use the same formula that was proposed above for the calculation of the arrester: (A + B * C / D) + (EF * ((G / (HJ * (- 1) + I) -L * (MN ) -R) + S) * W). To make it more clear in the process of illustrating the operation of the algorithm, I will replace the letters with numbers. Go.
We have a formula line at the input.

The operands are pulled out relative to the operation sign, one on the left and the other on the right. The sequence of operations within the fragment is directly protected by the priority of the processing sequence with substitution of the result. The unary and binary “-” issues are resolved within the addition / subtraction block.
So I think that there is not even a lot of explanation needed. Well, it's also clear where the name comes from. As you can see, there are no sorts as a class, there are no restrictions on the length of the formula and the number of nested groups. Everything is at the level of trivial searches and replacements. In order not to produce scraps of strings, it is enough to use StringBuilder (java) instead of String, which allows you to transform a string without producing unnecessary entities. But most importantly - all this is understandable at the level of simple intuitive perception.
To compare the algorithms, we present them in the same notation.
The algorithm for the arrester is taken from the Wiki

Ping-Pong Algorithm

Thus, the Ping-Pong algorithm is as close as possible to human perception and requires a minimum amount of resources. It also requires a minimum of character analysis and decision-making procedures, and does not require a buffer to assemble numbers from numbers.
There are a lot of such intuitive algorithms, I think. So why are students still tormented with all kinds of crap invented in time immemorial?
I would be glad if this algorithm is useful to someone.
The source of the description of the arrester will be a description from Lafore R .: L29 Data structures and algorithms in Java. Classic Computers Science. 2nd ed. - SPb .: Peter, 2013. - 704 s, recommended as the most popular and adequate on this issue, however, as well as on other commonly used algorithms.
Well, that is, we compare different algorithms with different ideologies.
To visualize the sequence of work on the formula (OPN), the following graph is given on page 158:

Already here you can see the adjustment of the algorithm to the wrong for a person property of sequential reading of symbolic information. For a person, the priority allocation of expression fragments and the construction of a further calculation scheme according to the priorities of these fragments are more characteristic. Therefore, in this case, the scheme will look like this in reality:

As you can see, an incorrect initial message for character-by-character parsing of an expression not only leads to distortion of infix notation processing, but also significantly complicates the picture of the actual analysis of complex formulas with multiple parentheses. After all, the second scheme (Fig1) is both clearer and significantly shorter than that presented in Fig.4.15 of the analyzed source.
Further, I am forced to quote a rather lengthy quote from the source, in which "the owl is pulled onto the globe."
“As you can see, in the process of calculating the result of an infix arithmetic expression, you have to move around the expression in the forward and reverse directions. First, operands and operators are read from left to right. With the accumulation of information sufficient for the use of the operator, you begin to move in the opposite direction, “remember” the two operands and the operator and perform an arithmetic operation. If the operator is followed by another operator with a higher priority or parentheses, the use of the operator is deferred. In this case, the next, higher-priority operator is applied first, and then you go back (to the left) and apply the earlier operators.Let's start by moving in the forward and reverse direction. The fact is that apologists for OPN usually focus on the last stage of calculations, when already re-sorted characters are stacked and removed from there in a row, which of course makes this stage very effective, sort of. But after all, as we recall, the work on the arrears consists of TWO stages (p. 153):
Of course, the algorithm for performing such processing could be programmed directly, and yet, as mentioned earlier, it is easier to first convert the expression to a postfix record. ”(End of quote)
"1. Converting an arithmetic expression to another format called postfix notation.Oops! It turns out that they try to push out the advantages of the second stage, but the headache with the first stage is simply modestly mentioned in passing. This is not a rebuke to the author, the author writes cool - this is a misunderstanding of why this, rather muddy, method is considered the main one in the analysis of formulas and is taught in the corresponding specialties.
2. Calculation of the result by postfix recording. ”(End of quote)
However, let's look carefully at stage one. Fortunately, the author provides a chic table for this (p. 153):

Most of all, I liked the last line. Tell me, for God's sake, how it can be sequentially pulled out of the STACK here and get a sane result. A system of two stacks, separately for operands and separately for operations, will still work, but with one stack ...
But this is not even about that. How many and what sortings should be done to make postfix from an infix (familiar to us) record? Why break the normal human logic of students for the sake of the ancient method? I’m even afraid to imagine how, for example, such a formula would look like: (A + B * C / D) + (EF * ((G / (HJ * (- 1) + I) -L * (MN) -R) + S ). And did you manage to present it at once?
Thus, we can say that the conversion from infix to postfix records already carries unjustifiably high costs for the implementation of complex obscure algorithms for sorting source data. Moreover, the number of returns at this stage will clearly exceed the resources required to process the infix (normal) record. Well, the processing of such a postfix record itself is somehow not limited to primitive pulling in a row from the stack, but requires an appropriate processor and additional resources.
We illustrate the sequence of required operations (OPN) with a small example.

Table 1. The procedure for calculating a fragment of the formula
But this is not all, because if the numbers consist of more than one digit, then you need to put a buffer to assemble the number of individual digits before placing them on the stack or output line.
I have no task to retell the method of calculating the arrester, so those who are particularly interested can read about it in the original source, especially since it is really cool written. Therefore, we turn to the Ping-Pong method (algorithm) announced in the title of the article.
Immediately make a reservation, there are a lot of methods (algorithms) for parsing formulas. You can name the method of recursive descent and the methods of building trees and others. I have not found Ping-Pong on the network, although, so I think, it is used quite often. Why he received such a name will become clear from the illustrations.
So, we proceed to the analysis of the algorithm. Let's start with some definitions for ease of presentation.
Priority - the dominance of one operation or grouping over others. The algorithm uses three priorities: 0 - operations "±"; 1 - operations "* /%"; 2 - grouping with parentheses “()”. Note: functions and work with them are not considered in this article. Functions are just a separate layer that does not affect the priority of operations.
A fragment is a part of a formula that can be passed for a lower level calculation. That is, a fragment is both a part of the formula framed by brackets and containing operations of the 0th and 1st levels, and a trivial fragment containing two operands and the sign of the operation between them.
For the convenience of illustration, we will use the same formula that was proposed above for the calculation of the arrester: (A + B * C / D) + (EF * ((G / (HJ * (- 1) + I) -L * (MN ) -R) + S) * W). To make it more clear in the process of illustrating the operation of the algorithm, I will replace the letters with numbers. Go.
We have a formula line at the input.

The operands are pulled out relative to the operation sign, one on the left and the other on the right. The sequence of operations within the fragment is directly protected by the priority of the processing sequence with substitution of the result. The unary and binary “-” issues are resolved within the addition / subtraction block.
So I think that there is not even a lot of explanation needed. Well, it's also clear where the name comes from. As you can see, there are no sorts as a class, there are no restrictions on the length of the formula and the number of nested groups. Everything is at the level of trivial searches and replacements. In order not to produce scraps of strings, it is enough to use StringBuilder (java) instead of String, which allows you to transform a string without producing unnecessary entities. But most importantly - all this is understandable at the level of simple intuitive perception.
To compare the algorithms, we present them in the same notation.
The algorithm for the arrester is taken from the Wiki

Ping-Pong Algorithm

Thus, the Ping-Pong algorithm is as close as possible to human perception and requires a minimum amount of resources. It also requires a minimum of character analysis and decision-making procedures, and does not require a buffer to assemble numbers from numbers.
There are a lot of such intuitive algorithms, I think. So why are students still tormented with all kinds of crap invented in time immemorial?
I would be glad if this algorithm is useful to someone.
