April 23, 2018 at 18:46Q # quantum teleportation
- Transfer
I will say right away: no matter how much I would like it, quantum teleportation will not allow my grandmother to be transferred from the village to my apartment. Granny knows that I like all kinds of quantum things, and instead of money and socks, she decided to send me a quantum state for my birthday. Here we talk about something else - the transfer of quantum information.
This is the second article in a series on quantum programming. It is assumed that the reader is already familiar with the first part .
Unfortunately, you cannot send a qubit either by email or by sending. They are transmitted through special quantum channels, and in the village and the Internet something appeared recently.
But maybe grandmother will be able to transmit quantum information through a classical communication channel (for example, via the Internet or a telephone line)? The problem is that the range of possible values of the quantum state is continuous, therefore, for its accurate description, an infinite number of classical bits will be required . My grandmother is a very busy person, and she does not have time to gain so many bits.
She has already begun to lose all hope, and then I say: "Granny, everything is in order." Remember, last Wednesday we made Bell’s fortune over tea? You can transfer a quantum state through it! Such transmission of a quantum state using classical communication channels is called quantum teleportation. We will try to figure out how it works - in theory and in code.
For everything described below to work, my grandmother and I must prepare Bell’s state: put her qubit | G⟩ and my qubit | F⟩ into a state of entanglement. I part with my grandmother, but I take my qubit (half of Bell’s fortune) with me. Our qubits will be in a state of entanglement, regardless of how much distance separates them - several kilometers or several billion light-years.
Remember, we discussed the remarkable property of entangled states - the connectedness of the measurement results of the corresponding qubits? If my grandmother measures the state of her qubit, it will affect my qubit (regardless of the distance). Below we will actively use this property.
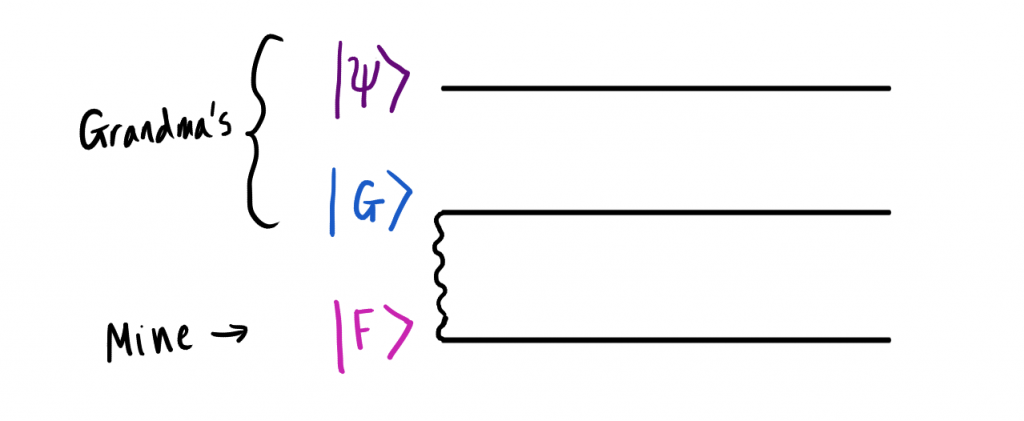
The initial state will be described using the above diagram. In the upper left corner is the subject of all our efforts - the qubit that my grandmother wants to send me. It is in an unknown state, which can be represented as follows:
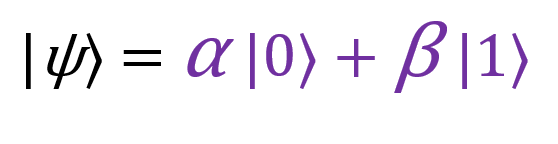
In addition, it has at its disposal the qubit | G⟩, which, as we just discussed, is confused with my qubit, | F⟩ (this relationship is shown by a wavy line). Now two qubits are in the Bell state, which is described by the formula
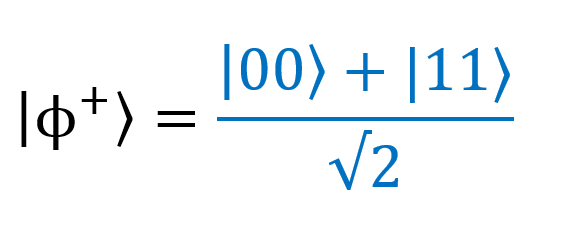
First, we confuse the grandmother qubit | G⟩ with the state | ψ⟩. You’ll soon understand why. In a previous article, we learned that two qubits can be confused using a circuit consisting of a CNOT valve and a Hadamard valve. Let's see how this process is represented using a quantum chain.
[To better understand these notations in diagrams of quantum circuits, I recommend that you briefly read the article Quantum Circuits and Gates - Introductory Course .]
If you add the CNOT valve, the circuit takes the following form. The state that is fed to the CNOT input can be written as | ψ⟩ | G⟩, where the first input corresponds to the upper wire, the second to the middle one. If we substitute the definitions of | ψ⟩ and | G⟩, we get:
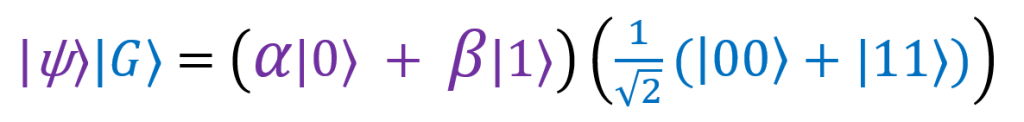
Expand the brackets:
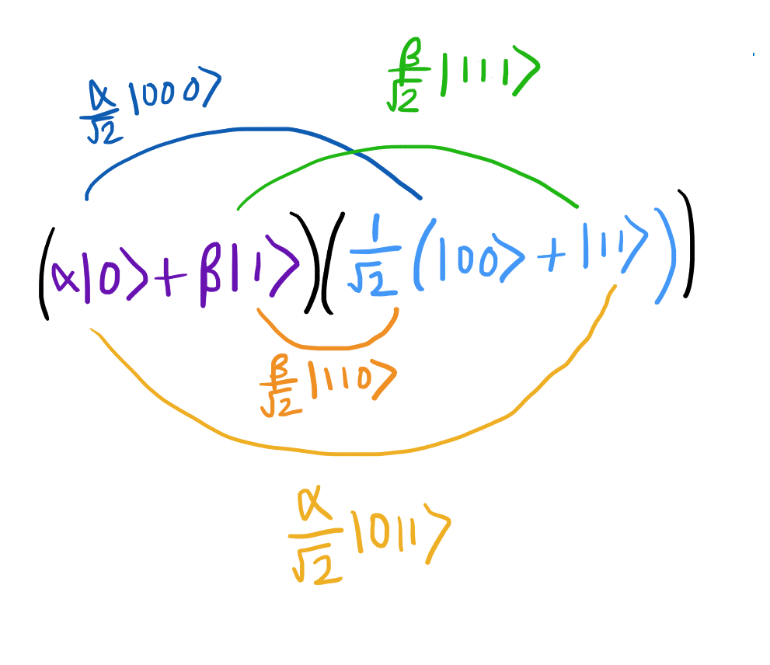
Thus, it is input
. Each of these terms passes through the CNOT valve. In the first article, we saw how the CNOT operates and how it processes two qubits. The most attentive readers have already noticed that all of our terms - | 000〉, | 011〉, | 100〉 and | 111〉 - consist of three qubits. In this case, the first is used as the control qubit, and the second is controlled (see below).
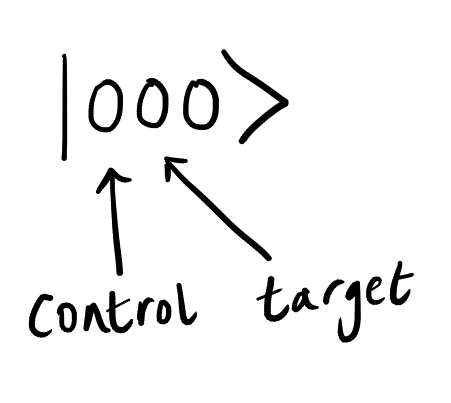
When the control qubit is | 1〉, the value of the controlled qubit is reversed. Thus, CNOT turns the set of qubits | 100〉 into | 110〉, and | 111〉 into | 101〉. All other conditions remain the same.
This means that the state of three qubits after CNOT gate will be described by the following equation: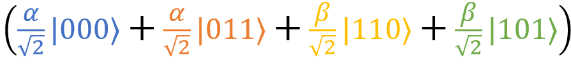
.
The second stage of entangling the qubit | G⟩ with the state | ψ⟩ is the application of the Hadamard valve to the first qubit. Here's what it looks like in a quantum circuit diagram:
Let me remind you that the Hadamard gate converts | 0〉 and | 1〉 to states
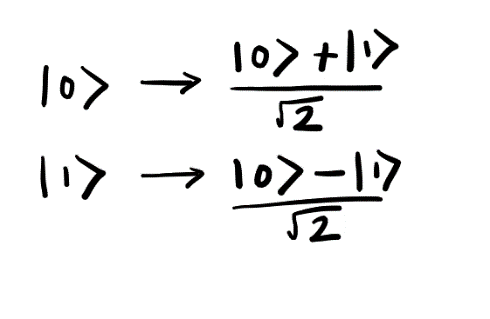
After the CNOT gate, qubits were in state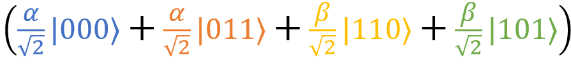. We apply the Hadamard valve to the first qubit of each term. The result looks pretty messy:
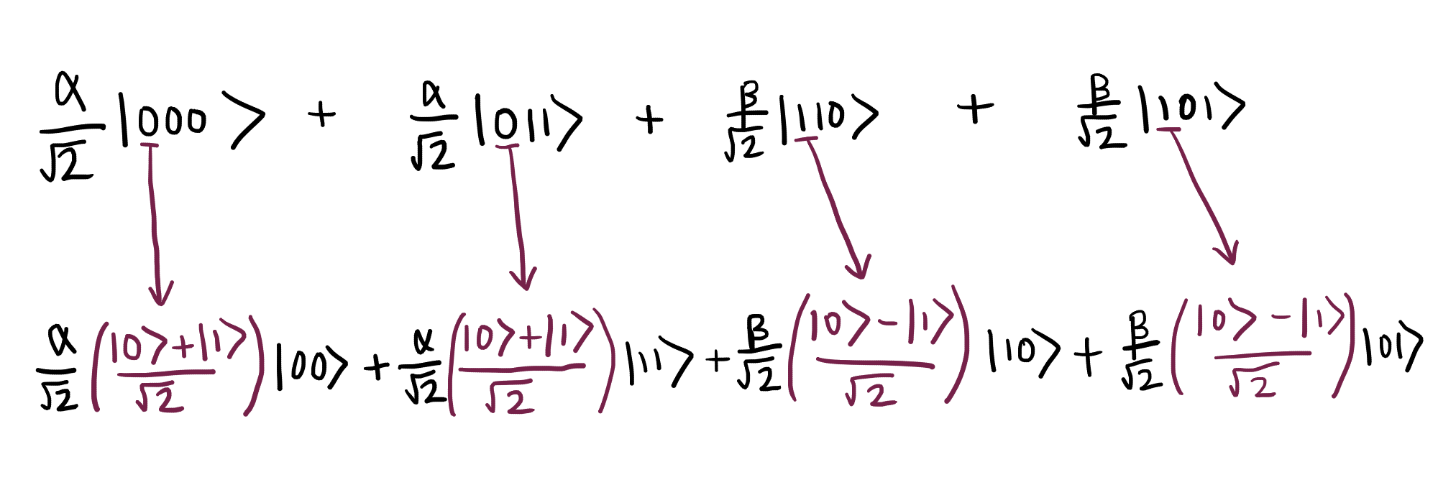
So, we got
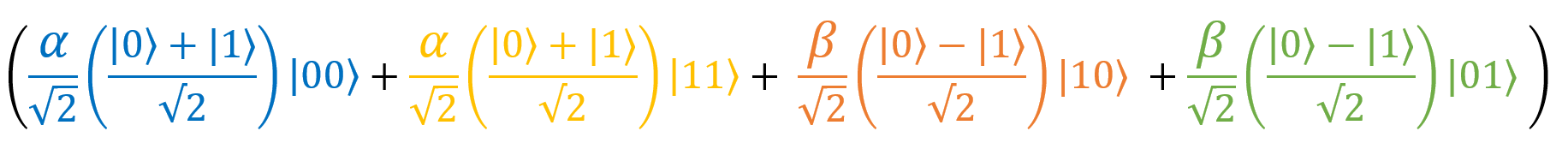
Let's comb our formula a bit. As you can see, in the first term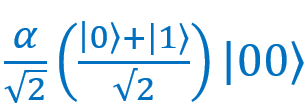
there are two fractions with a denominator of √2. Multiply them:
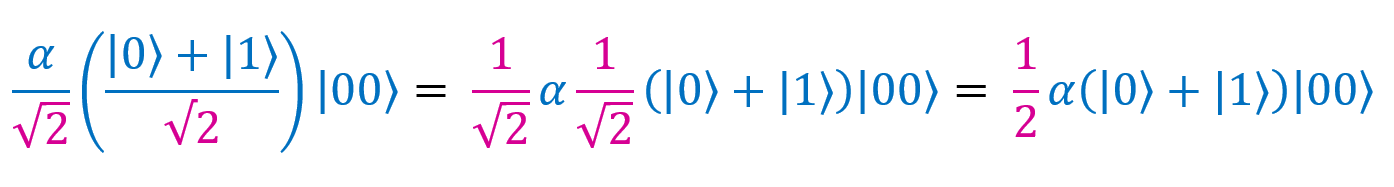
If we apply a similar operation to other terms, we get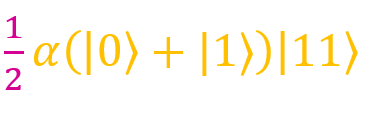
, 
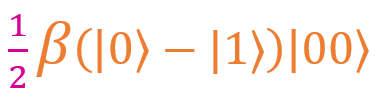and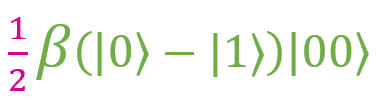 
. As you can see, each fraction has a factor of 1/2. If you put it out of the brackets, we get:
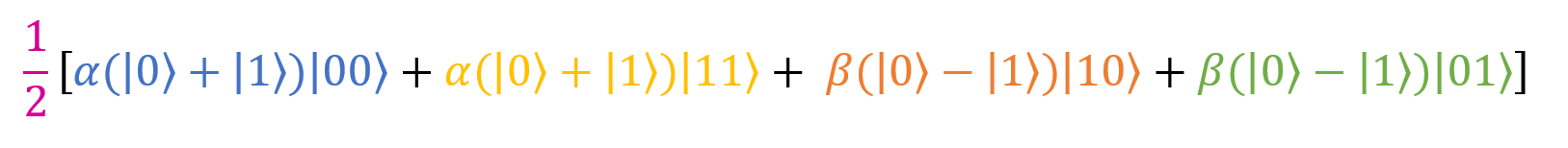
It already looks better. Now we’ll open the brackets (this will simplify our work in the next step). As an example, I will give calculations for the term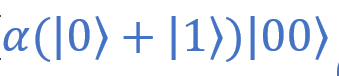
.
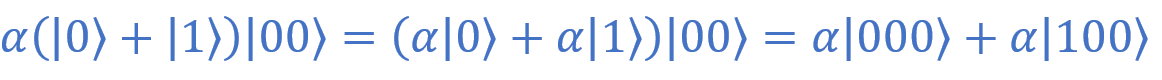
The rest "the reader is invited to do as an exercise." To be honest, I usually ignore such tempting offers. Here's what the remaining terms will look like if you expand the brackets:
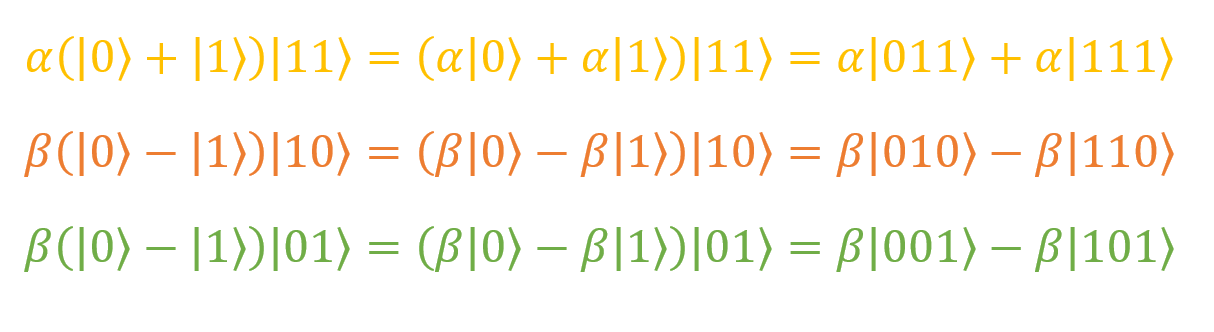
Their sum is
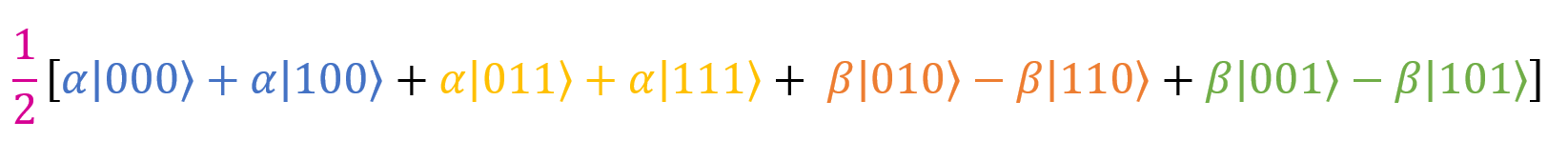
So, we confused grandmother’s qubit | G⟩ with qubit | ψ⟩. Now measure them. But before that, the results must be brought to a more convenient understanding.
This is the last time, honestly. Here are all the possible results of measuring the first and second qubits: 00, 01, 10, 11. So far we do not know what our third qubit will be in each of these cases. We group the terms in such a way as to understand what state the third qubit will be in, namely, my qubit | F⟩.
So far, our result looks like this:
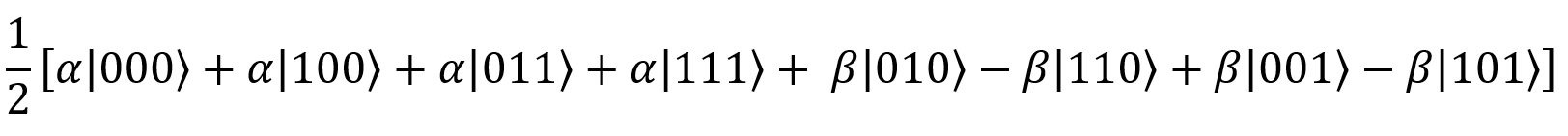
Select the first and second qubits of each term:
Consider the cases in which the first and second qubits are equal to | 00〉. The terms correspond to them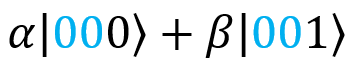
. They can be transformed as follows:
The same can be done for the cases | 01〉, | 10〉 and | 11〉.
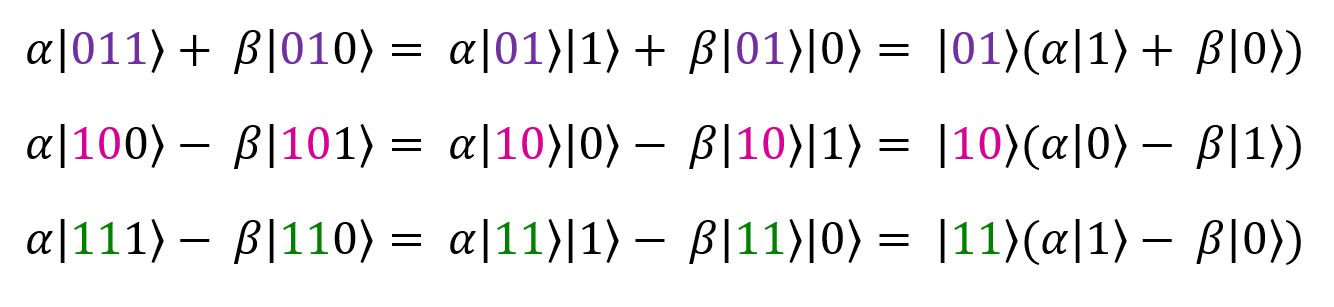
After conversion, the expression takes the following form:
Excellent.
This is how our chain looks with added dimension symbols. Notice the doubles after the dimension characters. They correspond to the transfer of classical bits, which are the results of measurements.
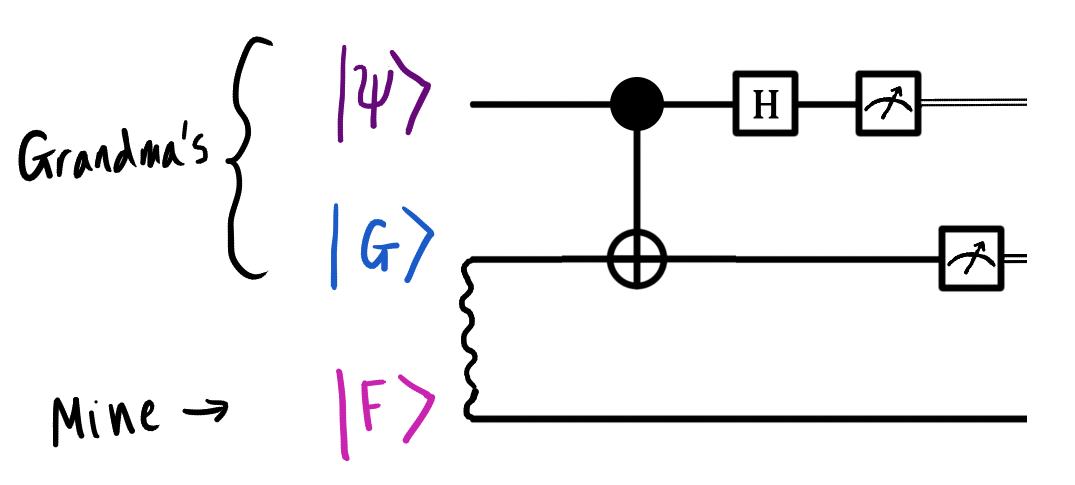
My grandmother also measures her two qubits, | G⟩ and | ψ⟩. As we have already said, a total of four measurement results are possible: 00, 01, 10, or 11. When a qubit is measured, the superposition of its states collapses. Suppose we measured the state of the first qubit | ψ⟩ and got 0. The superposition collapses, and we only have the terms that are consistent with this measurement result (0), that is, the following:
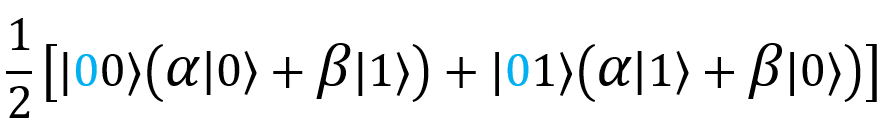
Suppose now that we measured the state of the second qubit, | G⟩, and obtained 0. The superposition collapses. There remains the only term that is consistent with both measurement results (0 and 0), that is, the following:
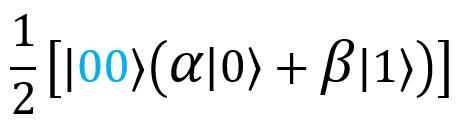
Now we know what state the third qubit is in (that is, my qubit | F⟩): in state
.
What if, as a result of the measurement, we get 01? Let us return to our result:
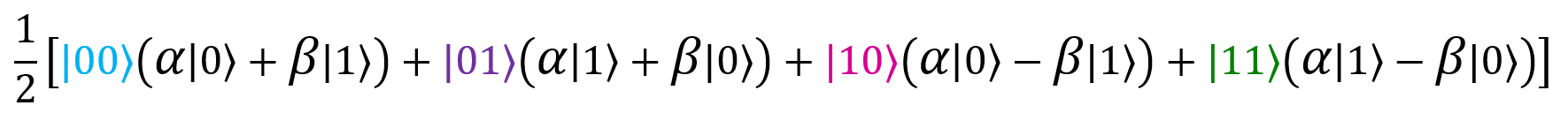
Arguing by analogy, we will understand that the only term that corresponds to the measurement result is 01 -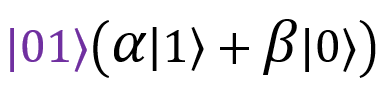
, which means that my qubit must be in a state 
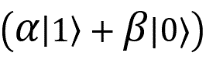. If after measurements the grandmother got the result 10, then I know that the third qubit is in a state 
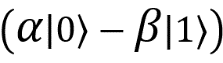, and if she got 11, then the third qubit is equal 
.
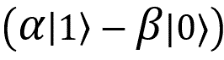This result can be presented in the form of a table:
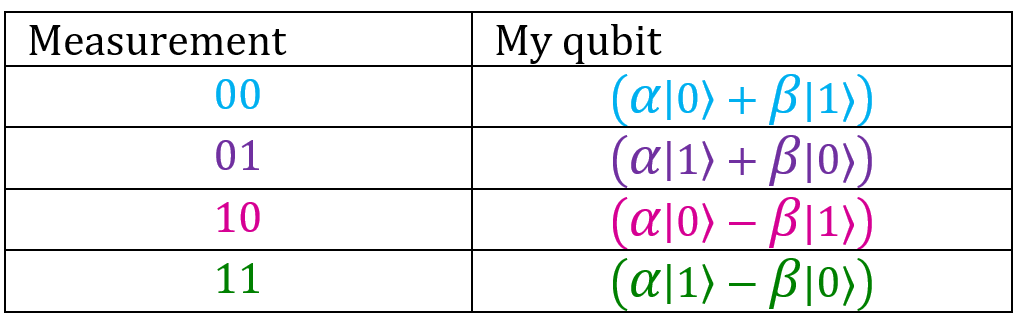
We settled on the fact that my grandmother measured the state of her two qubits, called me and told me about the result, so I know the state of my qubit. Remember that the unknown state we started with, | ψ⟩, was equal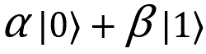
. We need to apply certain operations to my qubit in order to bring it into this state - the state that my grandmother wanted to send me (otherwise I will get something completely different).
Now it will be easy to do. Take a look at the table above. If the measurement result is 00, and my qubit is in a state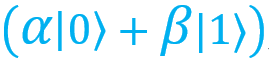
, then you do not need to perform any operations on it - it is already in the state | ψ⟩. This is the simplest case.
If the measurement result is 01, then my qubit is in a state
. If we compare it with the state | ψ⟩, it becomes clear that we need to swap the coefficients for | 0〉 and | 1〉. To do this, just pass my qubit through the NOT valve, that is, the X valve, and get the desired result 
.
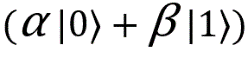With a measurement of 10, my qubit is in a state
. Compare it with | ψ⟩. We have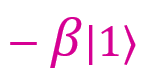 
, but it is necessary 
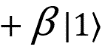. To make the desired reality, apply the valve Z, which changes sign.
And the last option is 11. In this case, my qubit is in a state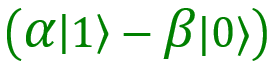
. Here you need to swap the coefficients for | 0〉 and 1〉, as well as the sign for 
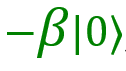. So my qubit must be passed through the valve X, and then through Z. Then we get the desired result 
. We add these operations to the table.
Please note: if the first bit of the measurement result is 1, then we use the valve Z, and if the second bit is 1, then we use the valve X. The final version of the circuit is shown below. We added valve Z, using the top wire as the control, and valve X, for which the second wire will be the control. At the same time, my qubit will be controlled (because it is precisely it that needs to be processed using gates).
So, we have shown that it is enough for grandmother to transmit only two classical bits (namely, the results of measuring the states of qubits | G⟩ and | ψ⟩) so that we can find out the state of the qubit unknown before. Thanks to the phenomenon of quantum entanglement, information from the grandmother helps to find out the values of the coefficients α and β. At the same time, we managed to do without a quantum communication channel. Therefore, this method is called quantum teleportation.
So, we have a little understanding of the theory of quantum teleportation. It's time to move on to the code!
If you need help at any step, the finished code is available here (just clone or download the repository, open the QuantumTeleportation.sln file in Visual Studio and go to step 5).
Create a new project in Visual Studio like “Application Q #” and give it some simple and clear name - for example, QuantumTeleportation.
Download a copy of the code with examples of quantum computing on your computer. To do this, clone or download the repository .
Now you need to replace all the code in the Operation.qs file with the code from the TeleportationSample.qs file, which is located in the Quantum> Samples> Teleportation section here .
Replace all the code in the Driver.cs file with the contents of the Program.cs file.
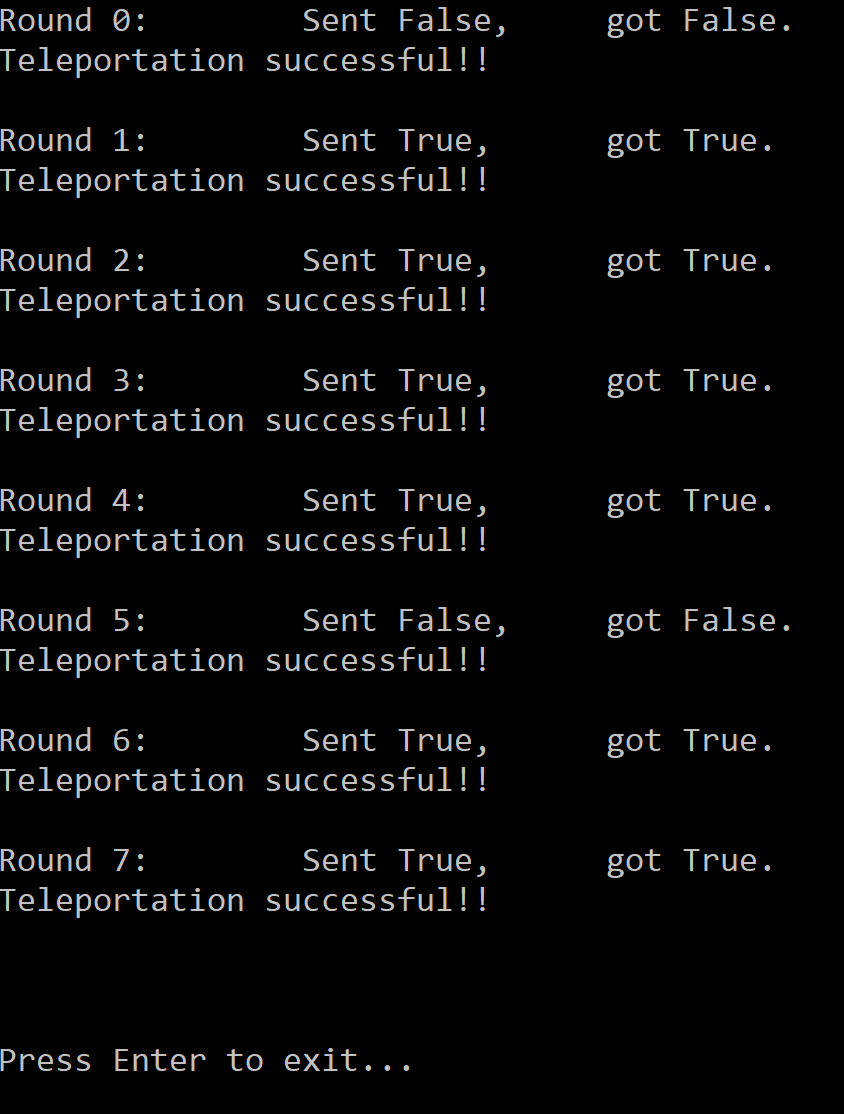
Click on the “start” button to run the code. The results for iterations 0–8 will be displayed. They should look something like this:
In fact, you can figure it out without my help - the code is remarkably commented. We simply compare it with the theory discussed above - it will be easy.
In the first part of the article, we talked about three qubits: a qubit in an unknown state | ψ⟩ and two qubits in a Bell state (one from my grandmother, the second from me). These three qubits in the Teleport operation correspond to the msg qubits (unknown state that my grandmother sends me), here (my grandmother’s qubit) and there (my qubit F, where | ψ⟩ is the forwarded state).
As already discussed, my grandmother and I prepared a couple of qubits in the Bell state beforehand. One of them is with my grandmother, the second - with me. Therefore, at the very beginning we need to confuse her qubit, which is called here , with mine, there . In the code, the Hadamard valve and the CNOT valve are used for this:
We will use our circuit diagram. I will add symbols to it as they appear in the code.
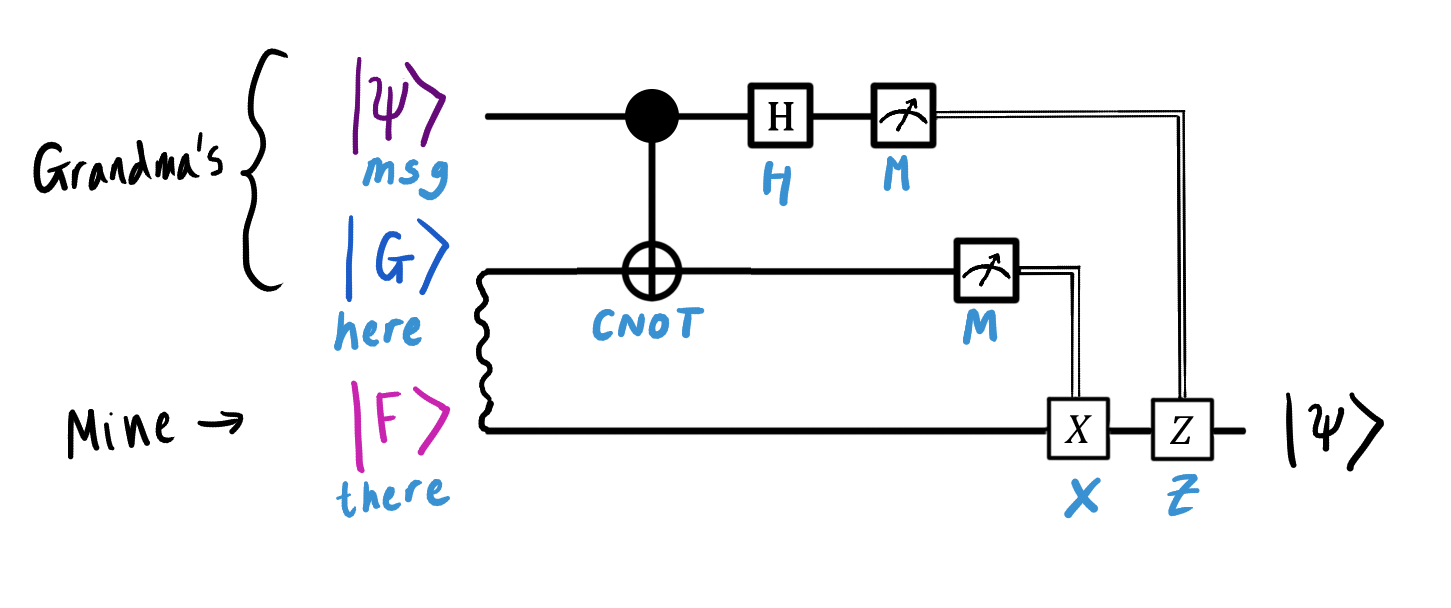
Repeating the operations described at the beginning of the article, we confuse grandmother's qubit here with unknown quantum state msg . The CNOT gate and the Hadamard gate in the diagram correspond to the following lines of code:
Then we measured the first and second qubits, msg and here. My grandmother informed me about the results of these measurements by telephone. The conditions of the if statement correspond to these events:
As we discussed at the end of the first part of this publication, after receiving the measurement results, I need to change the state of my qubit so that it matches the qubit | ψ⟩, that is, msg. As we said, if the measurement result of the first qubit is 1, then my qubit ( there ) must be passed through gate Z. This operation is shown above. If the measurement result of the second qubit is 1, then my qubit must be passed through the X valve.
Done! Now my qubit is in exactly the state that my grandmother wanted to convey to me.
Let's think about how, using the Teleport operation just discussed, you can send a message. My grandmother was already quite comfortable with quantum teleportation and now sends me not an unknown quantum state, but a known one - a message of one bit length. Suppose I asked my grandmother if she turned on the kettle. The answer will be one of two possible messages - yes or no.
First, we select the register into two qubits, the Boolean message that we will forward ( msg ), and my qubit, ( there ), with which the grandmother will transmit the message. Remember that the numbering of register elements starts at 0 (the same as in arrays). The result looks like this:
Qubit msg, which we have selected, is initially in the state | 0〉 (this is the default state for all allocated qubits). A grandmother’s message about whether the kettle is on can take one of two values - yes or no. If the answer is no, then nothing else needs to be done - such a message corresponds to the state | 0〉, in which the qubit msg is initially located. If the answer is yes, that is | 1〉, then we need to pass the qubit msg through the quantum gate NOT in order to put it into the state shown below.
Next, the grandmother transfers the status to me using the Teleport operation.
Then we measure the state of my qubit, there.
As a result, I get a 1-bit message and find out if I can count on hot tea. So dozens of years of research in the fields of quantum mechanics and computing have found a very important application.
If you run the code, the results of the transfer of various Boolean states that are contained in the Driver.cs file will be displayed on the screen .
On this we will end.
This is the second article in a series on quantum programming. It is assumed that the reader is already familiar with the first part .
Articles from the cycle:
Unfortunately, you cannot send a qubit either by email or by sending. They are transmitted through special quantum channels, and in the village and the Internet something appeared recently.
But maybe grandmother will be able to transmit quantum information through a classical communication channel (for example, via the Internet or a telephone line)? The problem is that the range of possible values of the quantum state is continuous, therefore, for its accurate description, an infinite number of classical bits will be required . My grandmother is a very busy person, and she does not have time to gain so many bits.
She has already begun to lose all hope, and then I say: "Granny, everything is in order." Remember, last Wednesday we made Bell’s fortune over tea? You can transfer a quantum state through it! Such transmission of a quantum state using classical communication channels is called quantum teleportation. We will try to figure out how it works - in theory and in code.
Send grandmother quantum mail
Stage 0, preparatory
For everything described below to work, my grandmother and I must prepare Bell’s state: put her qubit | G⟩ and my qubit | F⟩ into a state of entanglement. I part with my grandmother, but I take my qubit (half of Bell’s fortune) with me. Our qubits will be in a state of entanglement, regardless of how much distance separates them - several kilometers or several billion light-years.
Remember, we discussed the remarkable property of entangled states - the connectedness of the measurement results of the corresponding qubits? If my grandmother measures the state of her qubit, it will affect my qubit (regardless of the distance). Below we will actively use this property.
Stage 1. Entangling the grandmother’s qubit with | ψ⟩
The initial state will be described using the above diagram. In the upper left corner is the subject of all our efforts - the qubit that my grandmother wants to send me. It is in an unknown state, which can be represented as follows:
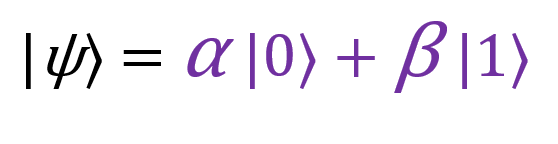
In addition, it has at its disposal the qubit | G⟩, which, as we just discussed, is confused with my qubit, | F⟩ (this relationship is shown by a wavy line). Now two qubits are in the Bell state, which is described by the formula
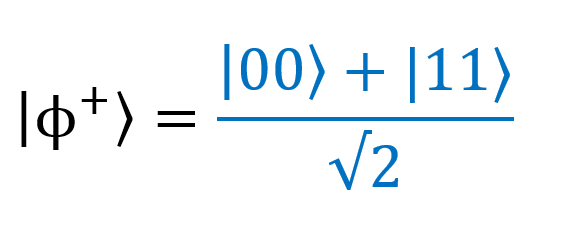
First, we confuse the grandmother qubit | G⟩ with the state | ψ⟩. You’ll soon understand why. In a previous article, we learned that two qubits can be confused using a circuit consisting of a CNOT valve and a Hadamard valve. Let's see how this process is represented using a quantum chain.
[To better understand these notations in diagrams of quantum circuits, I recommend that you briefly read the article Quantum Circuits and Gates - Introductory Course .]
CNOT Valve Application
If you add the CNOT valve, the circuit takes the following form. The state that is fed to the CNOT input can be written as | ψ⟩ | G⟩, where the first input corresponds to the upper wire, the second to the middle one. If we substitute the definitions of | ψ⟩ and | G⟩, we get:
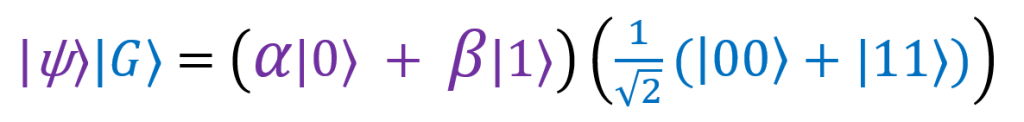
Expand the brackets:
Thus, it is input
. Each of these terms passes through the CNOT valve. In the first article, we saw how the CNOT operates and how it processes two qubits. The most attentive readers have already noticed that all of our terms - | 000〉, | 011〉, | 100〉 and | 111〉 - consist of three qubits. In this case, the first is used as the control qubit, and the second is controlled (see below).When the control qubit is | 1〉, the value of the controlled qubit is reversed. Thus, CNOT turns the set of qubits | 100〉 into | 110〉, and | 111〉 into | 101〉. All other conditions remain the same.
This means that the state of three qubits after CNOT gate will be described by the following equation:
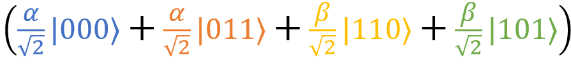.Hadamard Valve Application
The second stage of entangling the qubit | G⟩ with the state | ψ⟩ is the application of the Hadamard valve to the first qubit. Here's what it looks like in a quantum circuit diagram:
Let me remind you that the Hadamard gate converts | 0〉 and | 1〉 to states
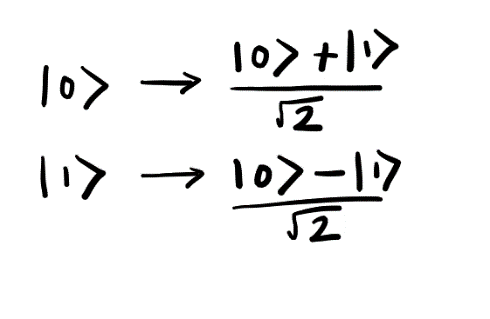
After the CNOT gate, qubits were in state
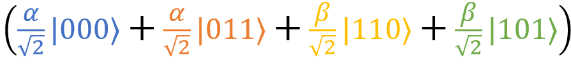. We apply the Hadamard valve to the first qubit of each term. The result looks pretty messy: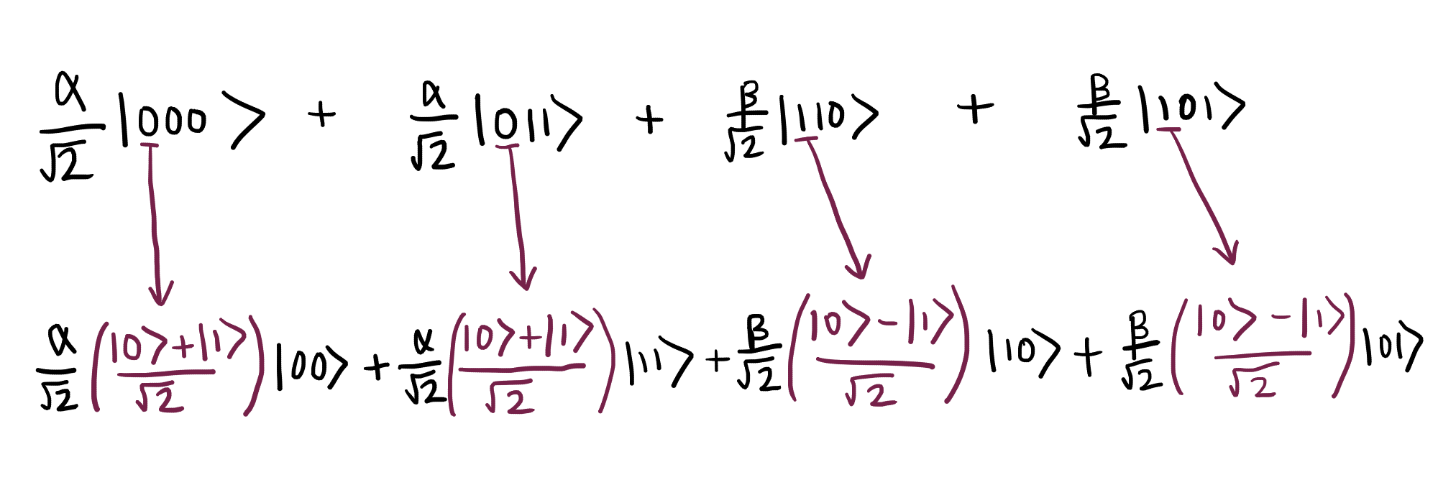 So, we got
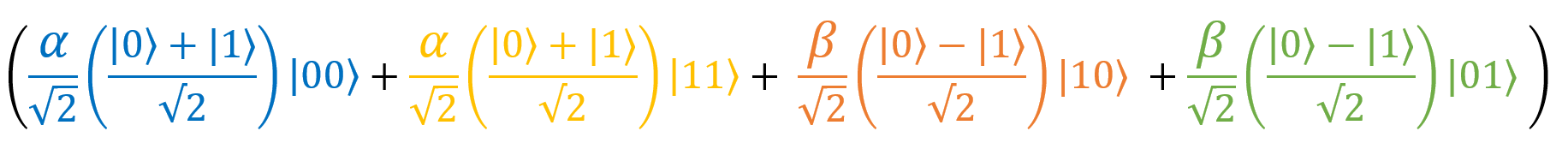
Remove excess
Let's comb our formula a bit. As you can see, in the first term
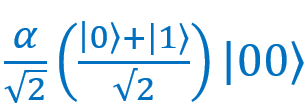there are two fractions with a denominator of √2. Multiply them: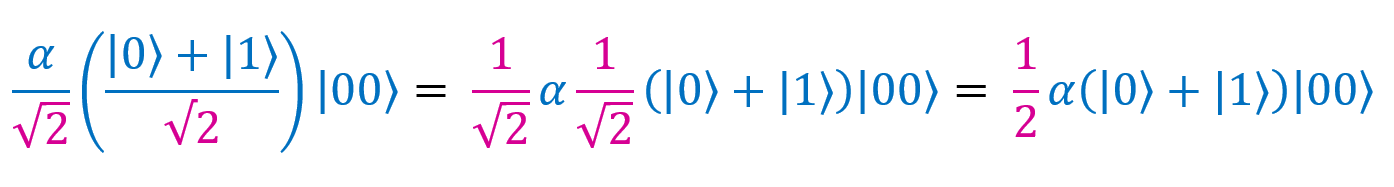 If we apply a similar operation to other terms, we get
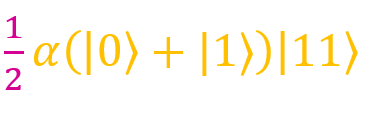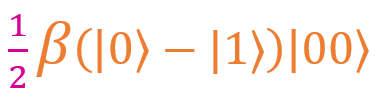, and . As you can see, each fraction has a factor of 1/2. If you put it out of the brackets, we get: 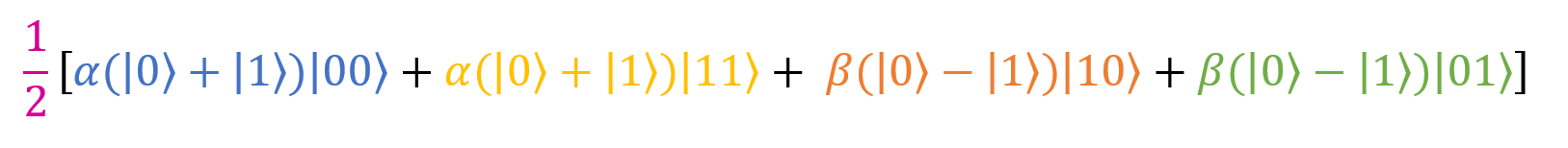It already looks better. Now we’ll open the brackets (this will simplify our work in the next step). As an example, I will give calculations for the term
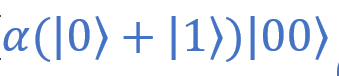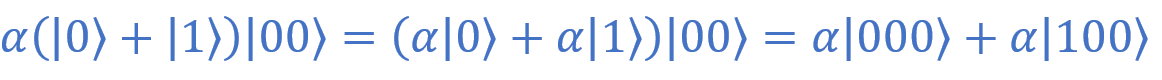
. The rest "the reader is invited to do as an exercise." To be honest, I usually ignore such tempting offers. Here's what the remaining terms will look like if you expand the brackets:
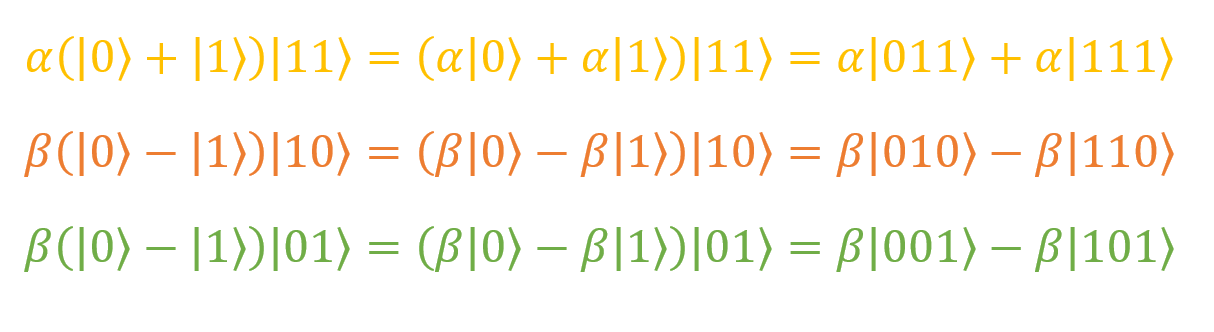
Their sum is
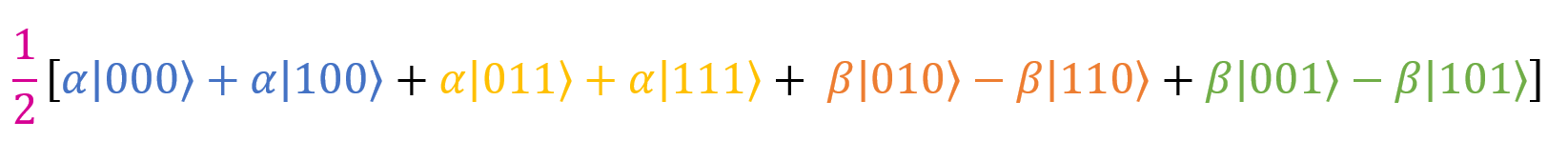
Stage 2. Measurement
So, we confused grandmother’s qubit | G⟩ with qubit | ψ⟩. Now measure them. But before that, the results must be brought to a more convenient understanding.
Clear the results again
This is the last time, honestly. Here are all the possible results of measuring the first and second qubits: 00, 01, 10, 11. So far we do not know what our third qubit will be in each of these cases. We group the terms in such a way as to understand what state the third qubit will be in, namely, my qubit | F⟩.
So far, our result looks like this:
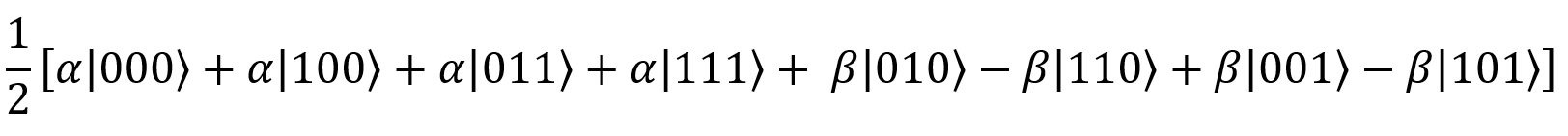
Select the first and second qubits of each term:
Consider the cases in which the first and second qubits are equal to | 00〉. The terms correspond to them
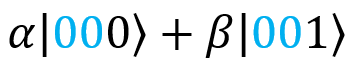. They can be transformed as follows: The same can be done for the cases | 01〉, | 10〉 and | 11〉.
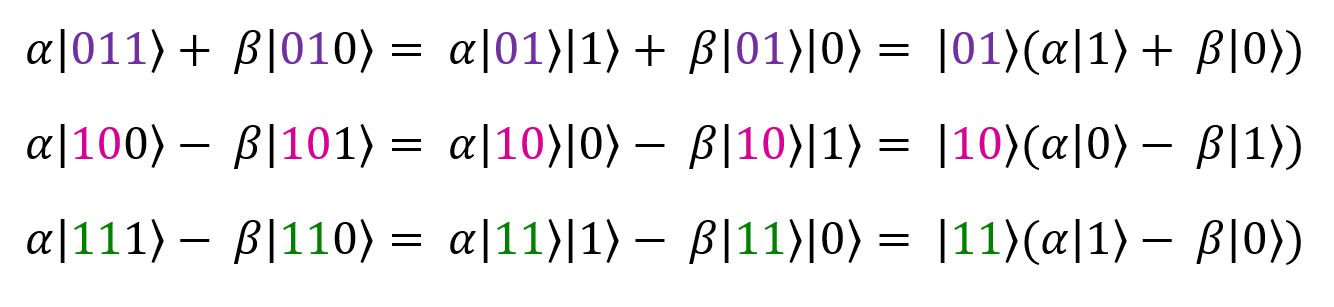
After conversion, the expression takes the following form:
Excellent.
Measurement
This is how our chain looks with added dimension symbols. Notice the doubles after the dimension characters. They correspond to the transfer of classical bits, which are the results of measurements.
My grandmother also measures her two qubits, | G⟩ and | ψ⟩. As we have already said, a total of four measurement results are possible: 00, 01, 10, or 11. When a qubit is measured, the superposition of its states collapses. Suppose we measured the state of the first qubit | ψ⟩ and got 0. The superposition collapses, and we only have the terms that are consistent with this measurement result (0), that is, the following:
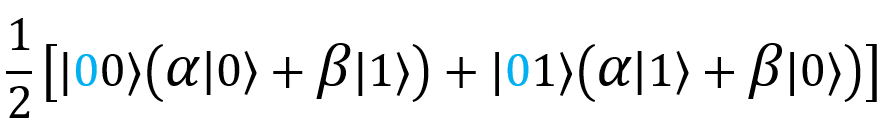
Suppose now that we measured the state of the second qubit, | G⟩, and obtained 0. The superposition collapses. There remains the only term that is consistent with both measurement results (0 and 0), that is, the following:
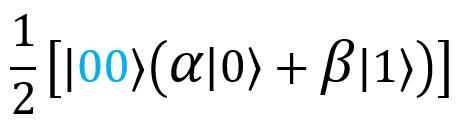
Now we know what state the third qubit is in (that is, my qubit | F⟩): in state
. What if, as a result of the measurement, we get 01? Let us return to our result:
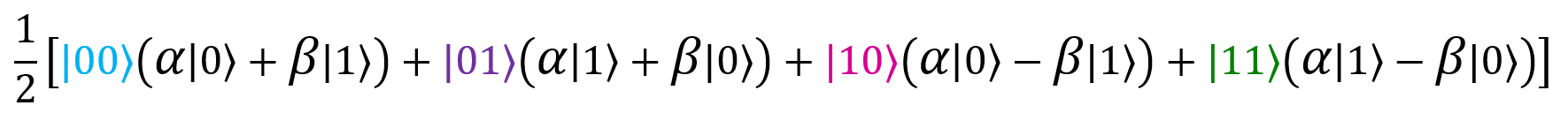
Arguing by analogy, we will understand that the only term that corresponds to the measurement result is 01 -
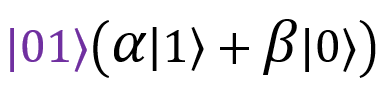, which means that my qubit must be in a state 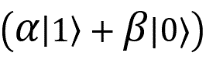. If after measurements the grandmother got the result 10, then I know that the third qubit is in a state 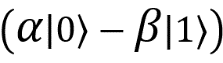, and if she got 11, then the third qubit is equal 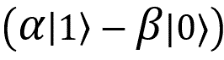.This result can be presented in the form of a table:
Stage 3. Transition of my qubit (F) to the state | ψ⟩
We settled on the fact that my grandmother measured the state of her two qubits, called me and told me about the result, so I know the state of my qubit. Remember that the unknown state we started with, | ψ⟩, was equal
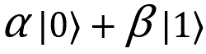. We need to apply certain operations to my qubit in order to bring it into this state - the state that my grandmother wanted to send me (otherwise I will get something completely different). Now it will be easy to do. Take a look at the table above. If the measurement result is 00, and my qubit is in a state
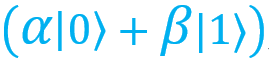, then you do not need to perform any operations on it - it is already in the state | ψ⟩. This is the simplest case. If the measurement result is 01, then my qubit is in a state
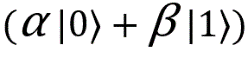. If we compare it with the state | ψ⟩, it becomes clear that we need to swap the coefficients for | 0〉 and | 1〉. To do this, just pass my qubit through the NOT valve, that is, the X valve, and get the desired result . With a measurement of 10, my qubit is in a state
. Compare it with | ψ⟩. We have 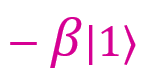, but it is necessary 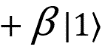. To make the desired reality, apply the valve Z, which changes sign. And the last option is 11. In this case, my qubit is in a state
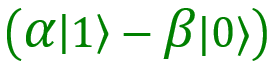. Here you need to swap the coefficients for | 0〉 and 1〉, as well as the sign for 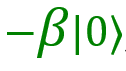. So my qubit must be passed through the valve X, and then through Z. Then we get the desired result . We add these operations to the table.Please note: if the first bit of the measurement result is 1, then we use the valve Z, and if the second bit is 1, then we use the valve X. The final version of the circuit is shown below. We added valve Z, using the top wire as the control, and valve X, for which the second wire will be the control. At the same time, my qubit will be controlled (because it is precisely it that needs to be processed using gates).
So, we have shown that it is enough for grandmother to transmit only two classical bits (namely, the results of measuring the states of qubits | G⟩ and | ψ⟩) so that we can find out the state of the qubit unknown before. Thanks to the phenomenon of quantum entanglement, information from the grandmother helps to find out the values of the coefficients α and β. At the same time, we managed to do without a quantum communication channel. Therefore, this method is called quantum teleportation.
Prepare and run the code
So, we have a little understanding of the theory of quantum teleportation. It's time to move on to the code!
If you need help at any step, the finished code is available here (just clone or download the repository, open the QuantumTeleportation.sln file in Visual Studio and go to step 5).
Stage 1. Create a project
Create a new project in Visual Studio like “Application Q #” and give it some simple and clear name - for example, QuantumTeleportation.
Step 2: Download a copy of the code
Download a copy of the code with examples of quantum computing on your computer. To do this, clone or download the repository .
Step 3: Modify the Operation.qs File
Now you need to replace all the code in the Operation.qs file with the code from the TeleportationSample.qs file, which is located in the Quantum> Samples> Teleportation section here .
Step 4: Modify the Driver.cs File
Replace all the code in the Driver.cs file with the contents of the Program.cs file.
Step 5. Save and run the project.
Click on the “start” button to run the code. The results for iterations 0–8 will be displayed. They should look something like this:
We understand how this code works
In fact, you can figure it out without my help - the code is remarkably commented. We simply compare it with the theory discussed above - it will be easy.
Stage 1. Teleportation
In the first part of the article, we talked about three qubits: a qubit in an unknown state | ψ⟩ and two qubits in a Bell state (one from my grandmother, the second from me). These three qubits in the Teleport operation correspond to the msg qubits (unknown state that my grandmother sends me), here (my grandmother’s qubit) and there (my qubit F, where | ψ⟩ is the forwarded state).
As already discussed, my grandmother and I prepared a couple of qubits in the Bell state beforehand. One of them is with my grandmother, the second - with me. Therefore, at the very beginning we need to confuse her qubit, which is called here , with mine, there . In the code, the Hadamard valve and the CNOT valve are used for this:
We will use our circuit diagram. I will add symbols to it as they appear in the code.
Repeating the operations described at the beginning of the article, we confuse grandmother's qubit here with unknown quantum state msg . The CNOT gate and the Hadamard gate in the diagram correspond to the following lines of code:
Then we measured the first and second qubits, msg and here. My grandmother informed me about the results of these measurements by telephone. The conditions of the if statement correspond to these events:
As we discussed at the end of the first part of this publication, after receiving the measurement results, I need to change the state of my qubit so that it matches the qubit | ψ⟩, that is, msg. As we said, if the measurement result of the first qubit is 1, then my qubit ( there ) must be passed through gate Z. This operation is shown above. If the measurement result of the second qubit is 1, then my qubit must be passed through the X valve.
Done! Now my qubit is in exactly the state that my grandmother wanted to convey to me.
Stage 2. TeleportClassicalMessage
Let's think about how, using the Teleport operation just discussed, you can send a message. My grandmother was already quite comfortable with quantum teleportation and now sends me not an unknown quantum state, but a known one - a message of one bit length. Suppose I asked my grandmother if she turned on the kettle. The answer will be one of two possible messages - yes or no.
First, we select the register into two qubits, the Boolean message that we will forward ( msg ), and my qubit, ( there ), with which the grandmother will transmit the message. Remember that the numbering of register elements starts at 0 (the same as in arrays). The result looks like this:
Qubit msg, which we have selected, is initially in the state | 0〉 (this is the default state for all allocated qubits). A grandmother’s message about whether the kettle is on can take one of two values - yes or no. If the answer is no, then nothing else needs to be done - such a message corresponds to the state | 0〉, in which the qubit msg is initially located. If the answer is yes, that is | 1〉, then we need to pass the qubit msg through the quantum gate NOT in order to put it into the state shown below.
Next, the grandmother transfers the status to me using the Teleport operation.
Then we measure the state of my qubit, there.
As a result, I get a 1-bit message and find out if I can count on hot tea. So dozens of years of research in the fields of quantum mechanics and computing have found a very important application.
If you run the code, the results of the transfer of various Boolean states that are contained in the Driver.cs file will be displayed on the screen .
On this we will end.
Resources
- More information is available on the Microsoft Quantum website.
- Download Quantum Development Kit
- Sign up for the Microsoft Quantum Newsletter
- Get the latest from Microsoft Quantum Blog