April 9, 2018 at 10:21Quantum Circuits and Gates - Introductory Course
- Transfer
- Tutorial
We continue the cycle of quantum articles. Today we delve into the formulas and understand how you can manipulate qubits - elementary computing units. In addition, we consider the principles of chains and algorithms. More details under the cut!
The purpose of this article is to help you quickly become familiar with the basic principles of quantum gates and understand how these gates are combined into chains that clearly represent quantum algorithms (some of which we will discuss in subsequent publications).
For your convenience, I will publish summary information about all the most important gates, circuit elements, etc. from the articles in this series in the form of a cheat sheet (so that you do not have to look for the necessary information for a long time). In my future articles, it will be called Quantum Computing: A Brief Reference.
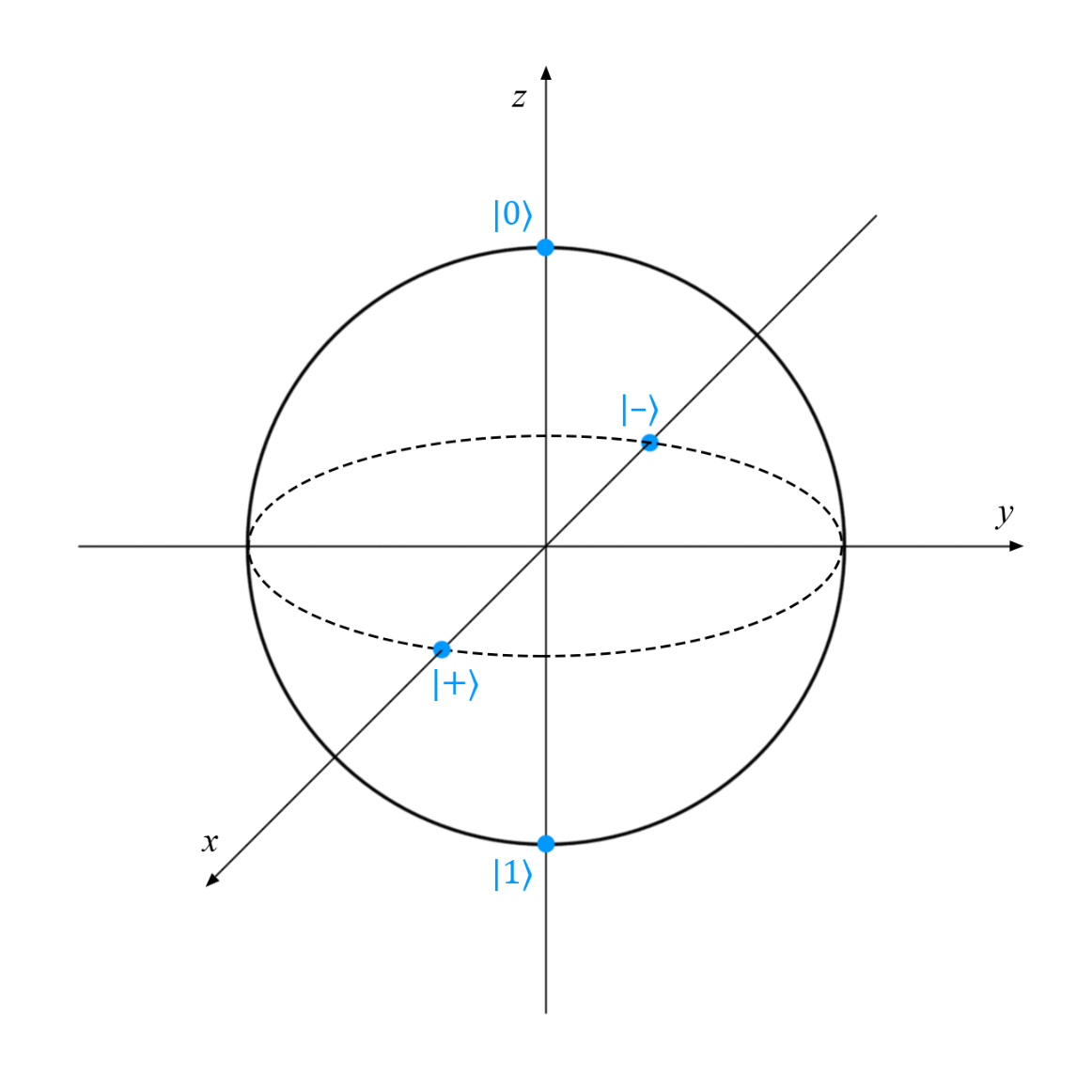
Let's start with the basics - with the notation of some common quantum states that we will subsequently manipulate:
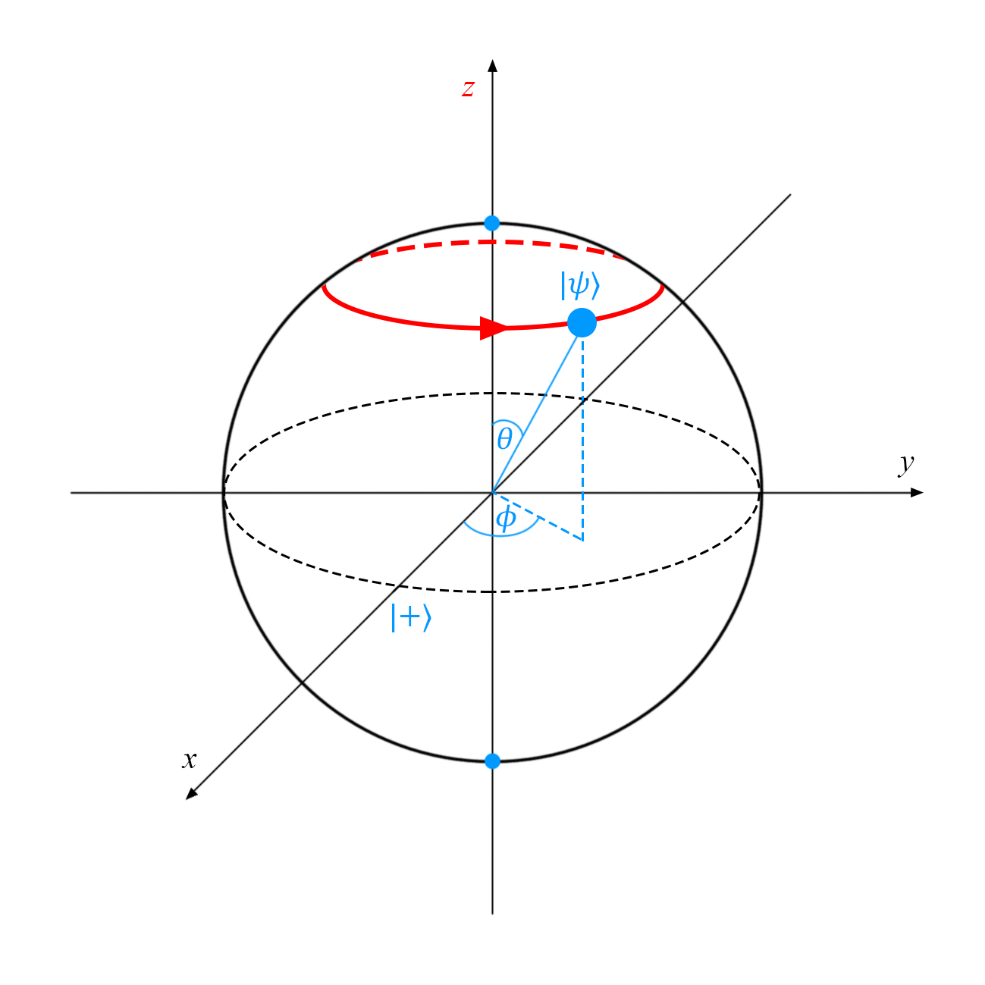
All of them are pure one-qubit states, so they can be represented as points on the Bloch sphere:
Now, there are four Bell states (they are also called EPR pairs, in honor of Einstein , Podolsky and Rosen - they are the authors of the ideas that Bell subsequently developed). These are the simplest examples of the quantum entanglement of two qubits:
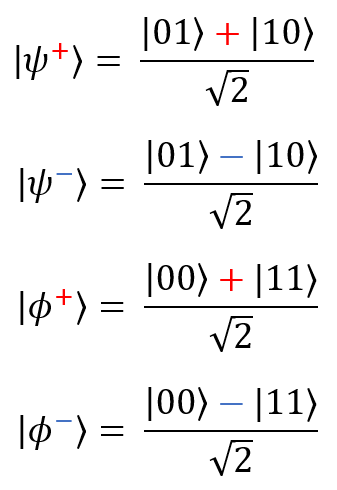
And finally, we will use the so-called GHC states (Greenberg - Horn - Zeilinger). Here is their general form (for n qubits) and the simplest form (for three qubits):
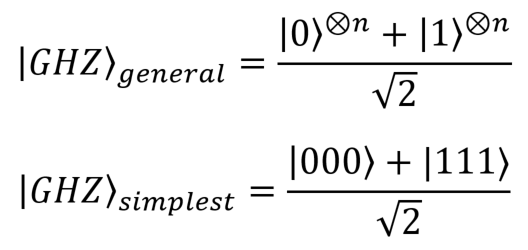
Bell’s and GHC’s states are very important because their behavior is fundamentally different from the predictions of the classical theory because of the level of entanglement in such systems (this principle of “maximum entanglement” will be considered in a future publication).
Rotation angles in quantum computing theory are measured in radians. The full circle (360 °) corresponds to 2π radians. Angles are measured counterclockwise. The values of the most important angles in degrees and in radians are shown below.
Before delving into the study of quantum gates, you should study the basics of constructing diagrams of quantum circuits (this will not take much time):
Here are the notations for the most important elements:
For more information, see the documentation here and in the book by M. Nielsen and I. Chang, “Quantum Information and Quantum Computing.”
One-qubit valves are naturally the simplest, so we will start with them. An operation performed by any one-qubit valve can be represented as a rotation of a vector characterizing the state of a qubit to another point of the Bloch sphere (see below).
The most basic one qubit valves are Pauli X, Y, and Z valves:
Gate X is very similar to the classic NOT gate: it converts | 0〉 to | 1〉, and | 1〉 to | 0〉. This operation is equivalent to rotating the vector on the Bloch sphere around the x axis by π radians (or 180 °).
The gate Y is expected to correspond to the rotation of the vector around the y axis by π radians. As a result of such an operation, the vector | 0〉 turns into i | 1〉, and | 1〉 into -i | 0〉.
Gate Z is a special case of a phase shift valve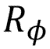
(see below) at phi = π = 180 °. It corresponds to the rotation of the vector around the z axis by π radians. It leaves the vector | 0〉 unchanged, and | 1〉 converts to - | 1〉.
The operation of these transformations is illustrated below using the Bloch sphere (the axis of rotation in each case is highlighted in red; you can click on the picture to enlarge it):
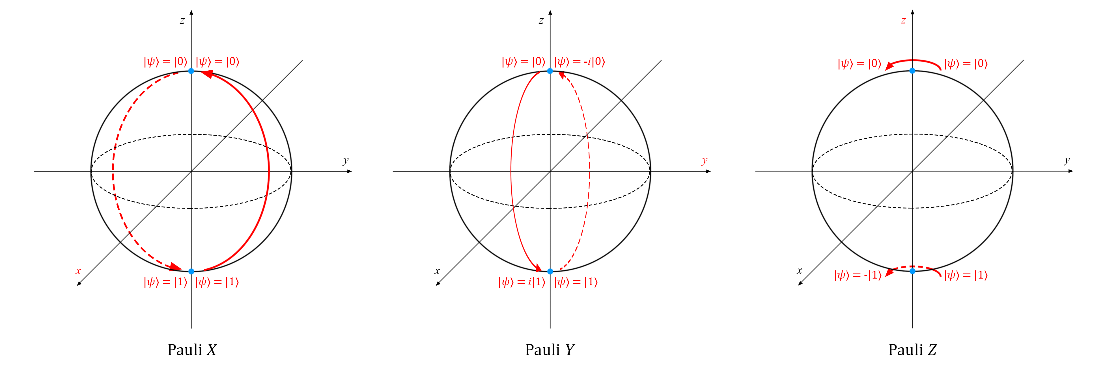
It is important to note that after applying the same Pauli gate twice to the qubit, it will return to its initial state (because after the vector rotates 2π radians or 360 ° around any axis, it will go to its initial position). As a consequence,
As
, etc.,..
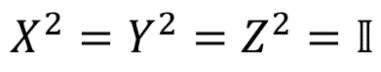
There II - designation of the identity matrix: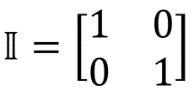
. The identity matrix is the matrix whose multiplication by an arbitrary matrix M (II) is equal to the matrix M: MII = IIM = M. The identity matrix corresponds to a quantum operation that does not change the quantum state. On the Bloch sphere, it looks like this:
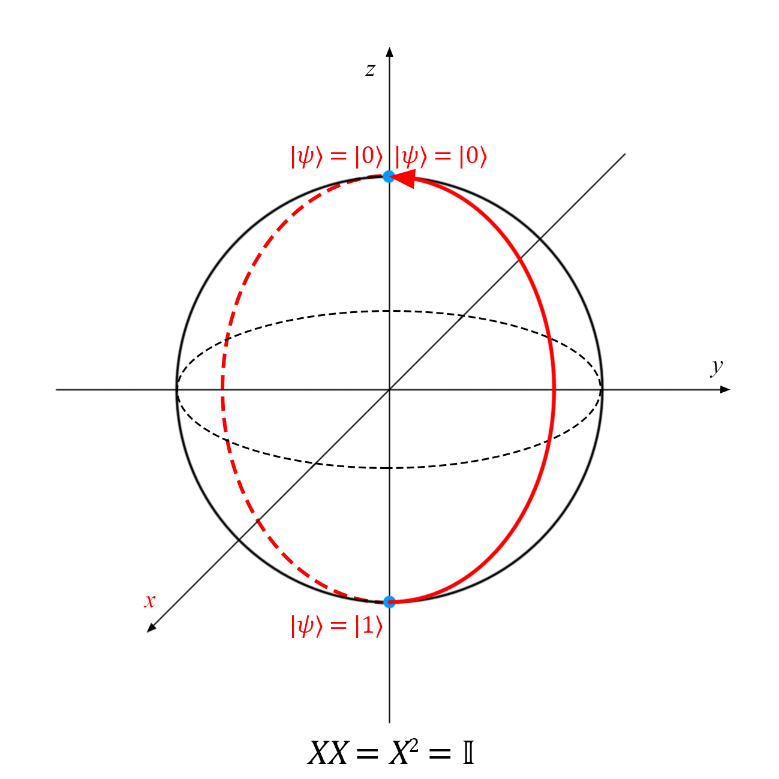
In view of this relationship, it is said that the Pauli matrix is squared equal to the identity matrix.
The following is a description of a few more important single qubit valves.
The Hadamard valve is especially important because it can be used to create a superposition of the states | 0〉 and | 1〉. This operation is most easily visualized using the Bloch sphere as a rotation around the x axis by π radians (180 °) followed by rotation around the y axis (clockwise) by π / 2 radians (90 °):
The phase transition valve is a fairly general operation, which has many useful uses. The most common variations are the phase shift gates by π / 4, π / 8 and the Pauli-gate Z, for which the parameter phi is π / 2, π / 4 and π, respectively. An example of a phase shift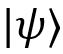
on a Bloch sphere:
Multi-qubit valves perform operations on two or more qubits. One of the simplest examples is the SWAP gate:
The SWAP gate swaps the two input qubits. For example, SWAP | 0〉 | 1〉 = | 1〉 | 0〉, and SWAP | 0〉 | 0〉 = | 0〉 | 0〉 (the full truth table is given in the cheat sheet for chains).
Another class of multi-qubit valves is the so-called controlled valves. At least one control and one controlled qubit is supplied to the input of any controlled valve , and the valve will perform an operation on the controlled qubit only if the control qubit is in a certain state. The gates that perform the operation with the control qubit | 1〉 are indicated by a filled circle on the wire of the control qubit. Valves that perform an operation with a control qubit equal to | 0〉 are indicated by an empty circle, as shown below.
In order to compose a matrix of any control valve, you need to add a single matrix in the upper left corner of the matrix of the desired valve, and fill in all other cells with zeros. Here is an example:
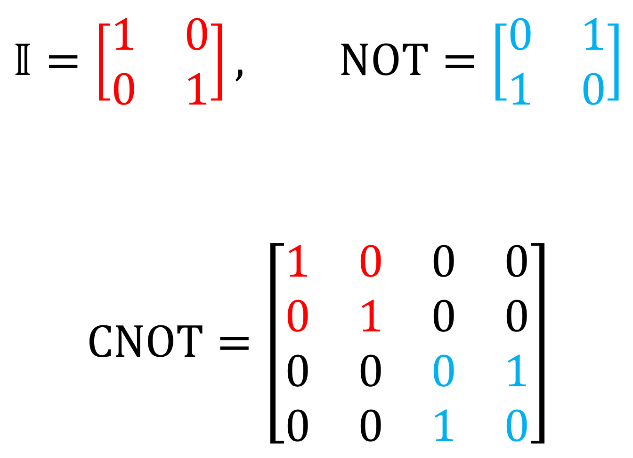
Common valves in Q # can be converted to control valves using the Controlled keyword, as described here (in the “Controlled” section at the bottom of the page). For example, the CNOT valve (recall that the NOT valve is equivalent to the Pauli X-valve) can be obtained with the command
where [control] is an array of input control qubits.
Other common controlled gates are described below (we highlighted the identity matrix in red and the source gate matrix in blue, as above):
As we mentioned in a previous publication , no matter what physical system we use to simulate a quantum computer, it should be possible to implement a “universal set” of gates. This means that any valid computational operation in our system must be convertible to a finite sequence of known gates. Here is an example of such a versatile set: Hadamard valve, phase shift valve, CNOT valve, and π⁄8 valve.
The universality property is much more interesting than it might seem at first glance. If a universal set of gates exists in a quantum computer, then any transformation that is allowed by the laws of quantum physics can be implemented using it. This means that with the help of a universal set you can not just execute any quantum program, but simulate any physical phenomenon. Therefore, the universality property allows the use of quantum computers to model molecules, superconductors, and any strange and beautiful quantum systems. This feature of quantum computers allows you to simulate physical phenomena, which in the future will allow quantum systems to surpass the potential of the most powerful supercomputers. Already not bored, right?
With the help of these (and some other) important gates, it is already possible to create fully functional quantum circuits! In the next publication, I will tell you how, with the help of this newly acquired knowledge, it is possible to realize the quantum Fourier transform - a very important operation that has a huge many practical applications.
Articles from the cycle:
Introduction
The purpose of this article is to help you quickly become familiar with the basic principles of quantum gates and understand how these gates are combined into chains that clearly represent quantum algorithms (some of which we will discuss in subsequent publications).
For your convenience, I will publish summary information about all the most important gates, circuit elements, etc. from the articles in this series in the form of a cheat sheet (so that you do not have to look for the necessary information for a long time). In my future articles, it will be called Quantum Computing: A Brief Reference.
Basics: quantum states
Let's start with the basics - with the notation of some common quantum states that we will subsequently manipulate:
All of them are pure one-qubit states, so they can be represented as points on the Bloch sphere:
Now, there are four Bell states (they are also called EPR pairs, in honor of Einstein , Podolsky and Rosen - they are the authors of the ideas that Bell subsequently developed). These are the simplest examples of the quantum entanglement of two qubits:
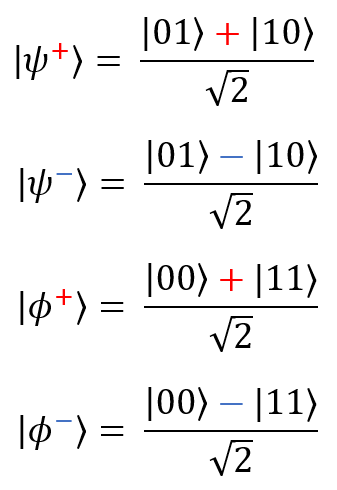
And finally, we will use the so-called GHC states (Greenberg - Horn - Zeilinger). Here is their general form (for n qubits) and the simplest form (for three qubits):
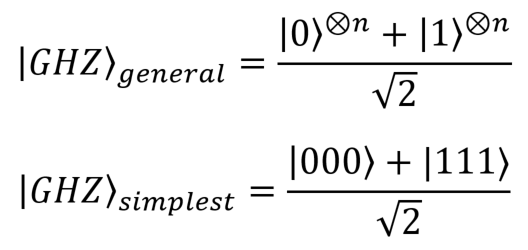
Bell’s and GHC’s states are very important because their behavior is fundamentally different from the predictions of the classical theory because of the level of entanglement in such systems (this principle of “maximum entanglement” will be considered in a future publication).
Theory: Radians
Rotation angles in quantum computing theory are measured in radians. The full circle (360 °) corresponds to 2π radians. Angles are measured counterclockwise. The values of the most important angles in degrees and in radians are shown below.
Basics: quantum circuit diagrams
Before delving into the study of quantum gates, you should study the basics of constructing diagrams of quantum circuits (this will not take much time):
- Time in a quantum diagram moves from left to right.
- Each qubit corresponds to a single horizontal line.
- Valves are usually indicated by squares. The type of gate is indicated by letters or other symbols in this square (there are exceptions to this rule. Usually these are qubit gates that have classic analogs (for example, the NOT gate).
- Some gates may correspond to several elements of the diagram (for example, the NOT gate).
- As a result of measuring the qubit, all superpositions collapse, the quantum properties of the qubit disappear, and it turns into a regular bit. Therefore, we can assume that the measuring element (shown below) receives a qubit and gives a classic bit. This operation in the Q # language corresponds to the Measure (bases: Pauli [], qubits: Qubit []) or M (qubit: Qubit) command at the base Z.
Here are the notations for the most important elements:
For more information, see the documentation here and in the book by M. Nielsen and I. Chang, “Quantum Information and Quantum Computing.”
Single quatt valves
One-qubit valves are naturally the simplest, so we will start with them. An operation performed by any one-qubit valve can be represented as a rotation of a vector characterizing the state of a qubit to another point of the Bloch sphere (see below).
The most basic one qubit valves are Pauli X, Y, and Z valves:
| Names | Matrix representation | Designations | View in Q # |
|---|---|---|---|
Pauli Gate X, X, NOT, Bit Switch, 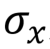 | 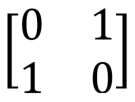 | 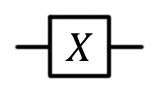 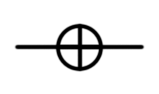 | X (qubit: Qubit) |
Pauli valve Y, Y, 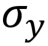 |  | 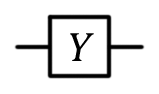 | Y (qubit: Qubit) |
Pauli valve Z, Z, phase switching, 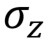 | 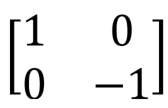 | 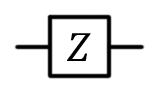 | Z (qubit: Qubit) |
The gate Y is expected to correspond to the rotation of the vector around the y axis by π radians. As a result of such an operation, the vector | 0〉 turns into i | 1〉, and | 1〉 into -i | 0〉.
Gate Z is a special case of a phase shift valve
(see below) at phi = π = 180 °. It corresponds to the rotation of the vector around the z axis by π radians. It leaves the vector | 0〉 unchanged, and | 1〉 converts to - | 1〉. The operation of these transformations is illustrated below using the Bloch sphere (the axis of rotation in each case is highlighted in red; you can click on the picture to enlarge it):
It is important to note that after applying the same Pauli gate twice to the qubit, it will return to its initial state (because after the vector rotates 2π radians or 360 ° around any axis, it will go to its initial position). As a consequence,
As
, etc.,.. 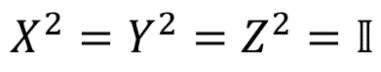There II - designation of the identity matrix:
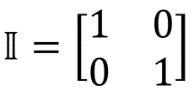. The identity matrix is the matrix whose multiplication by an arbitrary matrix M (II) is equal to the matrix M: MII = IIM = M. The identity matrix corresponds to a quantum operation that does not change the quantum state. On the Bloch sphere, it looks like this: In view of this relationship, it is said that the Pauli matrix is squared equal to the identity matrix.
The following is a description of a few more important single qubit valves.
| Names | Matrix representation | Designations | View in Q # |
|---|---|---|---|
| Hadamard Valve, H | 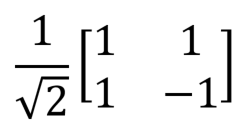 | 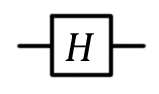 | H (qubit: Qubit) |
| Phase shift 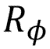| 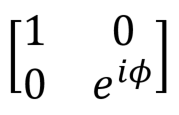 | 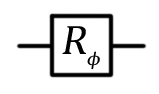 | R1 (theta: Double, qubit: Qubit) More generally, R (pauli: Pauli, theta: Double, qubit: Qubit) |
Phase shift,, 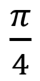 S | 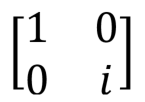 | 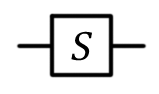 | S (qubit: Qubi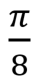t) |
 , T | 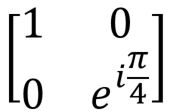 |  | T (qubit: Qubit) |
The phase transition valve is a fairly general operation, which has many useful uses. The most common variations are the phase shift gates by π / 4, π / 8 and the Pauli-gate Z, for which the parameter phi is π / 2, π / 4 and π, respectively. An example of a phase shift
on a Bloch sphere:Multi-valve
Multi-qubit valves perform operations on two or more qubits. One of the simplest examples is the SWAP gate:
| Names | Matrix representation | Designations | View in Q # |
|---|---|---|---|
| Swap | 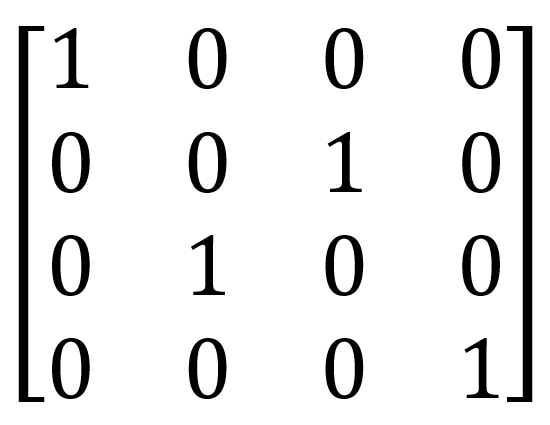 | 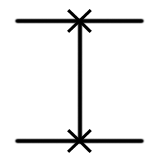 | SWAP (qubit1: Qubit, qubit2: Qubit) |
Another class of multi-qubit valves is the so-called controlled valves. At least one control and one controlled qubit is supplied to the input of any controlled valve , and the valve will perform an operation on the controlled qubit only if the control qubit is in a certain state. The gates that perform the operation with the control qubit | 1〉 are indicated by a filled circle on the wire of the control qubit. Valves that perform an operation with a control qubit equal to | 0〉 are indicated by an empty circle, as shown below.
In order to compose a matrix of any control valve, you need to add a single matrix in the upper left corner of the matrix of the desired valve, and fill in all other cells with zeros. Here is an example:
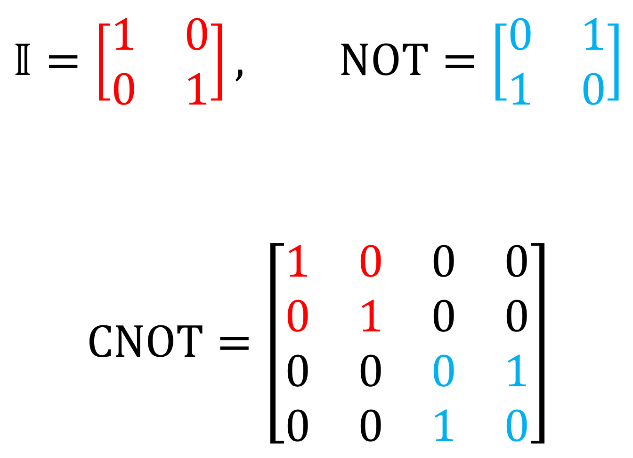
Common valves in Q # can be converted to control valves using the Controlled keyword, as described here (in the “Controlled” section at the bottom of the page). For example, the CNOT valve (recall that the NOT valve is equivalent to the Pauli X-valve) can be obtained with the command
(Controlled X)([control], (target))where [control] is an array of input control qubits.
Other common controlled gates are described below (we highlighted the identity matrix in red and the source gate matrix in blue, as above):
| Names | Matrix representation | Designations | View in Q # |
|---|---|---|---|
| CNOT |  | 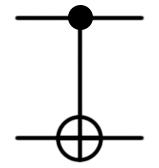 | CNOT (control: Qubit, target: Qubit) or (Controlled X) ([control], (target)); |
| CCNOT, Toffoli valve |  | 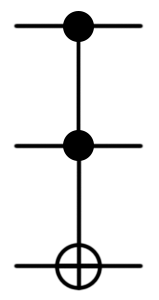 | CCNOT (control1: Qubit, control2: Qubit, target: Qubit) or (Controlled X) ([control1; control2], target); |
| CSWAP, Fredkin valve |  | 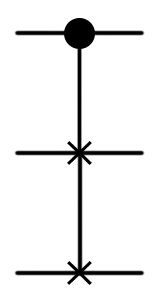 | (Controlled SWAP) ([control], (target)); |
Universal sets
As we mentioned in a previous publication , no matter what physical system we use to simulate a quantum computer, it should be possible to implement a “universal set” of gates. This means that any valid computational operation in our system must be convertible to a finite sequence of known gates. Here is an example of such a versatile set: Hadamard valve, phase shift valve, CNOT valve, and π⁄8 valve.
The universality property is much more interesting than it might seem at first glance. If a universal set of gates exists in a quantum computer, then any transformation that is allowed by the laws of quantum physics can be implemented using it. This means that with the help of a universal set you can not just execute any quantum program, but simulate any physical phenomenon. Therefore, the universality property allows the use of quantum computers to model molecules, superconductors, and any strange and beautiful quantum systems. This feature of quantum computers allows you to simulate physical phenomena, which in the future will allow quantum systems to surpass the potential of the most powerful supercomputers. Already not bored, right?
We are waiting for a lot of interesting things!
With the help of these (and some other) important gates, it is already possible to create fully functional quantum circuits! In the next publication, I will tell you how, with the help of this newly acquired knowledge, it is possible to realize the quantum Fourier transform - a very important operation that has a huge many practical applications.