Game with format
- Transfer
I suggest you play the game. I give you a square grid on which some cells are painted over and some may remain empty. We will call it a "template." For example, a grid can be one of these patterns:

You have a stack of transparent plastic sheets that match the size and shape of the grid, on which patterns of black dots are applied:

It is worth noting that in each of these patterns there are exactly three points, one point in each row and column. The six combinations shown are the only 3 × 3 grids with this property.
Your task is to collect a subset of transparent sheets and lay them on the template so that the dots cover all the filled squares, but do not fall into any of the empty ones. You can overlap several dots on any of the filled squares, but in general, you should strive to use as few sheets as possible. To make it more interesting, I propose to bid: for the correct coverage of the 3 × 3 template, I pay 3 dollars, but you must pay me 1 dollar for each sheet used. Is this a profitable bet for you?
Before moving on, I must say that not every possible template can be closed in accordance with such rules. Let's take an obvious example - no 3 × 3 template in which less than three squares are filled cannot be closed with any combination of six transparent sheets with dots. But I promise that I will offer you only patterns that can be closed with some combination of the available dot patterns; if I make a mistake in this, I’ll lose the money I put.
What will be the results of the game? If I give you the template marked above as “1 ″, then you can easily win: just choose a combination of a and bthat cover only all the filled squares. You pay $ 2, and I give you 3. Template 2, in which all nine squares are filled, may seem like the most difficult task. Obviously, it is impossible to close it with less than three sheets with patterns, because in total we need nine points; and it turns out that exactly three sheets are required. And in fact, there are two ways to cover a template with three sheets: a + d + e and b + c + f . Thus, this template gives us a break-even solution: you earn 3 dollars and spend 3 dollars.
Now we move on to template 3, in which there are filled squares and one is empty. It is clear that if you can close all nine squares with just three sheets, then we can close eight, right? I recommend you to try. In fact, for a single suitable combination, four sheets are needed: b + d + e + f . Therefore, my proposal should not be accepted: I can always give you a template with just one empty square, and your loss will total $ 1.
In a second I will return to the gaming table, but first, let me explain to you where this task came from. I once wrote about “estimation intervals”, which led me to research the topic of permutation matrices. I will repeat what I have already said:
In the comments, Barry Zipra asks the following question:
I think now the connection between the formats and my little game is obvious to you. The pattern of filled and empty squares is the format; sheets with dots indicate permutation matrices; To maximize your winnings in the game (or minimize losses), you need to answer Barry's first question by finding the minimum number of permutations, the combination of which will give us a given format.
For 3 × 3 matrices, we can solve this problem by exhaustive search, calculating the OR- sums of all possible combinations of six 3 × 3 permutation matrices 1, 2, 3, ..., 6 simultaneously. In a recent flight, I managed to do this with paper and a pencil. As a result, I got the following results:

Some of the numbers on this card are easy to explain. Six formats with only three single elements are the permutation matrices themselves. There are six of them, because for three elements 3 is possible! = 6 permutations. There are no formats with four single elements, and upon reflection, this can be understood: there can be no permutations that differ from each other by only one element. If you overlap any of the six sheets shown at the beginning of the article, you will get three, five or six points, but never four.
On the other hand, it does not surprise us that there is exactly one format with nine single elements, and that it requires three permutations to create it. And there are nine formats with eight single elements requiring ORfor four permutations. These will be templates with one empty square, like the template 3 shown above.
Based on these results, I began to think about what I would get when I put all 4 × 4 formats into the table.

It should be 4! = 24 patterns with four unit elements, and only one with all units created from an OR operation on four permutations. And there must be 16 formats that require five permutations, namely 16 matrices with a single zero element. The last forecast seemed to me less obvious than the rest.
I talked about the case with a single zero (or a single empty square) something like this: to close 15 squares with sets of four points each, we need at least four sets, otherwise we just don't have enough points. Therefore, a useful starting point would be one of the optimal schemes, covering all 16 squares without spaces or overlays. At this point, I got tired of drawing billions of points, so I started working with coins.

In this scheme, each coin denomination forms a permutation: no two coins in pennies, five, ten, or twenty-five cents are in the same column or line. We successfully closed all the filled squares, but, unfortunately, closed one empty in the lower right corner. Such a coin scheme is not an acceptable solution, but maybe we can fix it?

By moving a penny from an empty square to another square of the same column, we solve one problem, but create another: now the penny's layout is no longer a permutation - the second row contains two pennies.

That is, now we have to shift another penny in order to restore the property “one coin per column and row”. In this case, the filled square will inevitably remain open. The only way we can close this free square is to add a fifth permutation. I have run out of coin denominations, so I use the popular toroid brand for breakfast. Voila:

The movements made by me for this scheme are not unusual. If you try other templates, you can see for yourself that moving a penny covering the empty square to any other square of the fourth column (or fourth row) will lead to exactly the same situation. Similarly, the result of the game will be the same if one empty square is located anywhere else in the grid. And you can also start with another set of source permutations (provided that they cover all the squares).
This coin-shifting exercise shows that we can close any 4 × 4 pattern with a single empty square by a combination of no more than five permutations, but how do we know what exactly five are needed? Perhaps there is some completely different scheme that can handle just four permutations? Let's assume what such a scheme might look like. It should differ exactly in one position from some other permutation scheme that completely covers the grid of 16 squares. But no two permutations can differ at one single point. That is, the argument that there cannot be a scheme of four permutations covering 15 squares is essentially the same as the argument that no 4 × 4 format template can cover only five squares.
This argument can be generalized to matrices k× k : for any integer k , there must be at least k layout schemes that cannot be closed with less than k +1 permutations. But then we can make an even greater leap in reasoning: perhaps k +1 is the upper limit. Perhaps part of the answer to Barry's question is that for any k × k format schemes , no more than k + 1 permutations are required . At some point, I even had a “proof” of this hypothesis. Then I wrote a program that performed about the same work that I did with the points on the plane.
My program found 16 expected layout schemes requiring five permutations, but I also found many others. In total, she found 2,032 4 × 4 formats, which cannot be made up of less than five permutations. Then came a big surprise: the program also found 480 circuits requiring six permutations. Too much for my supposed upper bound.
One of these 480 problematic formats is as follows:
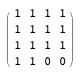
Looking at this pattern, I thought I understood the reasons for the fallacy of my previous reasoning. This matrix is exactly the same as a template with one zero, with only two zeros! (I really think this statement makes sense. Follow my discussion.) Suppose we start over with a set of four permutations that completely cover the entire grid, including two empty squares.

Then we can open each empty square in the same way as we did with the rearrangement of coins, but we need to be careful that these two sets of movements do not affect each other. (There is not much point in removing pennies from an empty square, and then immediately putting a penny there.) Here is a strategy for opening both empty squares that preserves the “one in column and row” permutation property:

When opening two empty squares, we will inevitably remove the coins from the two filled squares, which now need to be filled again. The most important thing here is that this problem cannot be eliminated by any single rearrangement, because two open filled squares are on the same line. To close both of these squares, we need two additional permutations.
Other ways to move coins avoid the location of two open squares in the same column or row, but they still fail all attempts to complete coverage with just five permutations. Try adding four rings to the diagram below. If you close both open blue squares, you will either close one of the empty squares, or two rings will appear on the same line.

That is, we now understand that six permutations are required to close the 4 × 4 format. Does this mean that the upper bound in the general case can be equal to k +2, and not k +1? Or maybe the correct formula is 2 k –2? In support of the last hypothesis, I propose to consider the following two ormates, which require 8 and 10 permutations, respectively:

Having been deceived several times with the upper limit of the minimum coverage of the format, before I offer another bet, I want to create a small space for errors. We already have direct evidence that up to 2 k –2 permutations may be required to cover a k × k format . Therefore, I will be generous and offer you 2 k dollars for the correct coverage, charging 1 dollar for each permutation. If k = 3 or k = 4, then you can definitely make money on this deal. But will it be beneficial for large k ? (Hint: I would play a game with such rules for real money.) Nobody agrees to accept such a bet? Sorry - I already spent my winnings.
Barry Zipra, who asked about the minimum coverage of an ormat, sent me a wonderful letter:
Definitely consistent.
First, in order to answer the small question that Barry left open, I will show you a lot of 16 permutations that successfully close his 7x7 “arrogant-triangular” matrix: I discovered it with a simple greedy search. My own attempts to find the upper bound were focused not on arrogant-triangular matrices, but on matrices, which I called “flags”, as this example for 7 × 7:

To correctly cover this matrix, 16 permutations are also required. To see the reasons for this, try swapping across the columns of the matrix, starting from the left edge, selecting in each column element 1 (and never 0) from different rows. Due to the block of zeros in the upper left corner, the first three elements of each permutation must be in lines 4-7. That is, each permutation “occupies” three of the last four rows in the first three columns, and the rest of the permutation can again fall into this row interval only once. It follows that each permutation can relate to only one element in the 4 × 4 block of unit elements in the lower right corner of the matrix, and at least 16 permutations are required to close all unit elements. To prove that 16 permutations is enough is not so difficult.
An analysis of this kind works for any odd k , and therefore we know that such matrices may require
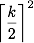
permutations. (For even k, the situation is less symmetrical, and I did not consider it in detail.)
These results give us a lower bound on the upper bound on the number of permutations that may be required to close the k × k format . But we have not proved that this is a valid upper bound. Are there other formats that need even more permutations? I believe not, but do not forget that almost all of my hypotheses made in this article turned out to be incorrect.

You have a stack of transparent plastic sheets that match the size and shape of the grid, on which patterns of black dots are applied:

It is worth noting that in each of these patterns there are exactly three points, one point in each row and column. The six combinations shown are the only 3 × 3 grids with this property.
Your task is to collect a subset of transparent sheets and lay them on the template so that the dots cover all the filled squares, but do not fall into any of the empty ones. You can overlap several dots on any of the filled squares, but in general, you should strive to use as few sheets as possible. To make it more interesting, I propose to bid: for the correct coverage of the 3 × 3 template, I pay 3 dollars, but you must pay me 1 dollar for each sheet used. Is this a profitable bet for you?
Before moving on, I must say that not every possible template can be closed in accordance with such rules. Let's take an obvious example - no 3 × 3 template in which less than three squares are filled cannot be closed with any combination of six transparent sheets with dots. But I promise that I will offer you only patterns that can be closed with some combination of the available dot patterns; if I make a mistake in this, I’ll lose the money I put.
What will be the results of the game? If I give you the template marked above as “1 ″, then you can easily win: just choose a combination of a and bthat cover only all the filled squares. You pay $ 2, and I give you 3. Template 2, in which all nine squares are filled, may seem like the most difficult task. Obviously, it is impossible to close it with less than three sheets with patterns, because in total we need nine points; and it turns out that exactly three sheets are required. And in fact, there are two ways to cover a template with three sheets: a + d + e and b + c + f . Thus, this template gives us a break-even solution: you earn 3 dollars and spend 3 dollars.
Now we move on to template 3, in which there are filled squares and one is empty. It is clear that if you can close all nine squares with just three sheets, then we can close eight, right? I recommend you to try. In fact, for a single suitable combination, four sheets are needed: b + d + e + f . Therefore, my proposal should not be accepted: I can always give you a template with just one empty square, and your loss will total $ 1.
Some background information
In a second I will return to the gaming table, but first, let me explain to you where this task came from. I once wrote about “estimation intervals”, which led me to research the topic of permutation matrices. I will repeat what I have already said:
- A permutation matrix is a square matrix with one 1 in each column and each row; the remaining elements are 0.
- Ormat is a superposition of permutation matrices formed by applying the Boolean function OR to the corresponding elements of the permutation matrices. For instance:
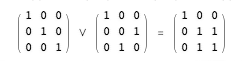
- Not all square matrices with elements (0,1) can be created by OR operations on permutation matrices, but there is an effective algorithm for determining whether a given matrix is a format.
- The total number of permutation paths in the format that can be passed through the unit elements of the matrix is equal to the permanent of the matrix. Defining a permanent is considered a complex computational task.
In the comments, Barry Zipra asks the following question:
A permanent tells us the maximum number of different permutations that can be summed through OR to obtain a given format, but what will be the corresponding minimum number? Also, in how many different ways can a minimum be reached?
I think now the connection between the formats and my little game is obvious to you. The pattern of filled and empty squares is the format; sheets with dots indicate permutation matrices; To maximize your winnings in the game (or minimize losses), you need to answer Barry's first question by finding the minimum number of permutations, the combination of which will give us a given format.
For 3 × 3 matrices, we can solve this problem by exhaustive search, calculating the OR- sums of all possible combinations of six 3 × 3 permutation matrices 1, 2, 3, ..., 6 simultaneously. In a recent flight, I managed to do this with paper and a pencil. As a result, I got the following results:

Some of the numbers on this card are easy to explain. Six formats with only three single elements are the permutation matrices themselves. There are six of them, because for three elements 3 is possible! = 6 permutations. There are no formats with four single elements, and upon reflection, this can be understood: there can be no permutations that differ from each other by only one element. If you overlap any of the six sheets shown at the beginning of the article, you will get three, five or six points, but never four.
On the other hand, it does not surprise us that there is exactly one format with nine single elements, and that it requires three permutations to create it. And there are nine formats with eight single elements requiring ORfor four permutations. These will be templates with one empty square, like the template 3 shown above.
Based on these results, I began to think about what I would get when I put all 4 × 4 formats into the table.

It should be 4! = 24 patterns with four unit elements, and only one with all units created from an OR operation on four permutations. And there must be 16 formats that require five permutations, namely 16 matrices with a single zero element. The last forecast seemed to me less obvious than the rest.
Trifle from pockets and breakfast cereals
I talked about the case with a single zero (or a single empty square) something like this: to close 15 squares with sets of four points each, we need at least four sets, otherwise we just don't have enough points. Therefore, a useful starting point would be one of the optimal schemes, covering all 16 squares without spaces or overlays. At this point, I got tired of drawing billions of points, so I started working with coins.

In this scheme, each coin denomination forms a permutation: no two coins in pennies, five, ten, or twenty-five cents are in the same column or line. We successfully closed all the filled squares, but, unfortunately, closed one empty in the lower right corner. Such a coin scheme is not an acceptable solution, but maybe we can fix it?

By moving a penny from an empty square to another square of the same column, we solve one problem, but create another: now the penny's layout is no longer a permutation - the second row contains two pennies.

That is, now we have to shift another penny in order to restore the property “one coin per column and row”. In this case, the filled square will inevitably remain open. The only way we can close this free square is to add a fifth permutation. I have run out of coin denominations, so I use the popular toroid brand for breakfast. Voila:

The movements made by me for this scheme are not unusual. If you try other templates, you can see for yourself that moving a penny covering the empty square to any other square of the fourth column (or fourth row) will lead to exactly the same situation. Similarly, the result of the game will be the same if one empty square is located anywhere else in the grid. And you can also start with another set of source permutations (provided that they cover all the squares).
This coin-shifting exercise shows that we can close any 4 × 4 pattern with a single empty square by a combination of no more than five permutations, but how do we know what exactly five are needed? Perhaps there is some completely different scheme that can handle just four permutations? Let's assume what such a scheme might look like. It should differ exactly in one position from some other permutation scheme that completely covers the grid of 16 squares. But no two permutations can differ at one single point. That is, the argument that there cannot be a scheme of four permutations covering 15 squares is essentially the same as the argument that no 4 × 4 format template can cover only five squares.
This argument can be generalized to matrices k× k : for any integer k , there must be at least k layout schemes that cannot be closed with less than k +1 permutations. But then we can make an even greater leap in reasoning: perhaps k +1 is the upper limit. Perhaps part of the answer to Barry's question is that for any k × k format schemes , no more than k + 1 permutations are required . At some point, I even had a “proof” of this hypothesis. Then I wrote a program that performed about the same work that I did with the points on the plane.
Went beyond the borders
My program found 16 expected layout schemes requiring five permutations, but I also found many others. In total, she found 2,032 4 × 4 formats, which cannot be made up of less than five permutations. Then came a big surprise: the program also found 480 circuits requiring six permutations. Too much for my supposed upper bound.
One of these 480 problematic formats is as follows:

Looking at this pattern, I thought I understood the reasons for the fallacy of my previous reasoning. This matrix is exactly the same as a template with one zero, with only two zeros! (I really think this statement makes sense. Follow my discussion.) Suppose we start over with a set of four permutations that completely cover the entire grid, including two empty squares.

Then we can open each empty square in the same way as we did with the rearrangement of coins, but we need to be careful that these two sets of movements do not affect each other. (There is not much point in removing pennies from an empty square, and then immediately putting a penny there.) Here is a strategy for opening both empty squares that preserves the “one in column and row” permutation property:

When opening two empty squares, we will inevitably remove the coins from the two filled squares, which now need to be filled again. The most important thing here is that this problem cannot be eliminated by any single rearrangement, because two open filled squares are on the same line. To close both of these squares, we need two additional permutations.
Other ways to move coins avoid the location of two open squares in the same column or row, but they still fail all attempts to complete coverage with just five permutations. Try adding four rings to the diagram below. If you close both open blue squares, you will either close one of the empty squares, or two rings will appear on the same line.

That is, we now understand that six permutations are required to close the 4 × 4 format. Does this mean that the upper bound in the general case can be equal to k +2, and not k +1? Or maybe the correct formula is 2 k –2? In support of the last hypothesis, I propose to consider the following two ormates, which require 8 and 10 permutations, respectively:

Another bet
Having been deceived several times with the upper limit of the minimum coverage of the format, before I offer another bet, I want to create a small space for errors. We already have direct evidence that up to 2 k –2 permutations may be required to cover a k × k format . Therefore, I will be generous and offer you 2 k dollars for the correct coverage, charging 1 dollar for each permutation. If k = 3 or k = 4, then you can definitely make money on this deal. But will it be beneficial for large k ? (Hint: I would play a game with such rules for real money.) Nobody agrees to accept such a bet? Sorry - I already spent my winnings.
Barry Zipra, who asked about the minimum coverage of an ormat, sent me a wonderful letter:
I will give hints for a short way to the hypothesis (in fact, just a hunch) that the behavior in the “worst case”, from the point of view of the minimum number of permutations necessary to obtain a given format, occurs for formats of the following form shown here for k = 7:
In order not to violate the existing terminology of matrices, I will call any (square) matrix of this type, i.e. such, all elements of which below the main sub-diagonal are 0, "arrogant-triangular." I can show (and I will do it!) That this arrogantly triangular format with k = 7 requires (at least) 16 permutations, and that starting from this value of k the number increases sharply. Therefore, personally, I definitely would not accept your bid of 2 k dollars.
The trick is to consider each format as a “shadow” of what I will call a “addmat” (addmat). Let P 1, P 2, ..., Pr be the matrices of permutations k × k; then their add-on will be the usual result of addition: S = P 1 + P 2 + ... + Pr , whose elements are positive integers, where one or more components of the permutations have 1, otherwise they are zero. The corresponding format is obtained by replacing each of the nonzero elements by 1 while preserving the zero elements. In this sense, the individual elements of the ormatate are the “shadows” of the positive elements of the admat.
The most important thing is that add-ons have a nice little property that its shadow does not have: all the sums of the row and column of the add-on elements are equal to the number of permutations that created them r .
Now let's think together. The above example of an arrogant triangular ormate (for k = 7) should be obtained from an addmat of the form
where a , b and all * are positive numbers. In particular, each * has a value of at least 1. Since all sums of rows and columns must be the same, the sum of a + b must be equal to b and all six * above them. Therefore, a has a value of at least 6. Similarly, the sum of a + b must be equal to the sum of a and all six * above it, that is, the value of b is also not less than 6. Therefore, a + b is not less than 12, that is, the OR sum creating a given format requires at least 12 permutations.
These considerations can be generalized to an arbitrary k , that is, we get not just “direct evidence” that up to 2 k –2 permutations may be required for the k × k format - this is a rigorous proof! But we can immediately improve it, at least for specific cases. If we try to get by with only 12 permutations for this arrogantly triangular ormate, then we will quickly have a problem. Obviously, we need a = b = 6, and therefore, all * above them are units (in order to get the sum 12 in this column). That is, we got an add-on
in which I want to draw your attention to the item marked as "@". To make the sum of its row equal 12, we need @ = 10. But this means that the sum of its column (with five * above it) is at least 15. But this cannot be! This means that we have to try to find larger values of a and / or b , that is, to create this add-on we need more permutation matrices.
It turns out that we cannot satisfy the condition of the sums of rows and columns until we get to a = b = 8. I will not explain all the steps, but just show the penultimate possible combination, a = 7, b = 8. The best you can hope in this case:
Notice that in the last two columns I gave as much “weight” as possible so that they were as close as possible to 7 and 8, and you could use the smallest possible value (10) as an element with five positive elements above it. Due to this, the last three rows and the three right rows have the same sum (15), but now there is a problem for the column with element 12: its sum is not less than 16. So, again, we are at a standstill. We can avoid a contradiction only with the following attempt:
Finally, all the sums of the rows and columns of the matrix are the same. It is worth considering that this may or may not be a real add-on for a set of 16 permutation matrices. I suspect that this is still an add-on, but I do not want to check it. All that we know is that it satisfies the necessary add-on condition, namely, all the sums of rows and columns are the same. (It would be great if this were a sufficient condition, but something tells me that this is not so.)
This example, which can be accurately reproduced at large values of k , makes us understand that the player offering the game is not only a winner rate of 2 k dollars. but also for (2 k+2) dollars and more. I experimented a bit with this and made sure that the number of permutation matrices would be much more than 2 k at k = 10. If I did everything right, then you will need 24 permutations (and possibly more if the analysis of the arrogant-triangular matrix shows us that it is not a real add-on). I am absolutely convinced that after careful reflection, the analysis can be simplified to a convenient and elegant proof. I'm just not sure if I have already made mistakes and if I built a house of cards from reasoning.
Does all of the above correspond to what you have come to?
Definitely consistent.
First, in order to answer the small question that Barry left open, I will show you a lot of 16 permutations that successfully close his 7x7 “arrogant-triangular” matrix: I discovered it with a simple greedy search. My own attempts to find the upper bound were focused not on arrogant-triangular matrices, but on matrices, which I called “flags”, as this example for 7 × 7:
{1,2,3,4,5,6,7} {2,1,4,3,6,7,5} {1,3,2,5,4,7,6} {1,3,4,2,6,5,7}
{2,3,1,5,6,4,7} {1,2,3,5,6,7,4} {1,2,4,5,3,6,7} {1,2,4,5,6,3,7}
{1,2,4,5,6,7,3} {1,3,4,5,2,6,7} {1,3,4,5,6,2,7} {1,3,4,5,6,7,2}
{2,3,4,1,5,6,7} {2,3,4,5,1,6,7} {2,3,4,5,6,1,7} {2,3,4,5,6,7,1}
To correctly cover this matrix, 16 permutations are also required. To see the reasons for this, try swapping across the columns of the matrix, starting from the left edge, selecting in each column element 1 (and never 0) from different rows. Due to the block of zeros in the upper left corner, the first three elements of each permutation must be in lines 4-7. That is, each permutation “occupies” three of the last four rows in the first three columns, and the rest of the permutation can again fall into this row interval only once. It follows that each permutation can relate to only one element in the 4 × 4 block of unit elements in the lower right corner of the matrix, and at least 16 permutations are required to close all unit elements. To prove that 16 permutations is enough is not so difficult.
An analysis of this kind works for any odd k , and therefore we know that such matrices may require
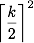
permutations. (For even k, the situation is less symmetrical, and I did not consider it in detail.)
These results give us a lower bound on the upper bound on the number of permutations that may be required to close the k × k format . But we have not proved that this is a valid upper bound. Are there other formats that need even more permutations? I believe not, but do not forget that almost all of my hypotheses made in this article turned out to be incorrect.





