About the rotation matrix in simple words
When Pythagoras sailed along the Yellow River, he saw off the shore, in a boat, a dozing fisherman, in a conical hat and with a bamboo fishing rod in his hands.
Bearing in mind that people of different mathematical backgrounds are looking at Habrahabr, however, the topic of linear transformations may well fall into their field of interest, due to its practical significance, I will try to talk about this as much as possible.

The triangular shape of the boat, hats and fishing rods above the water amazed the philosopher and mathematician so much that he froze as if bewitched.
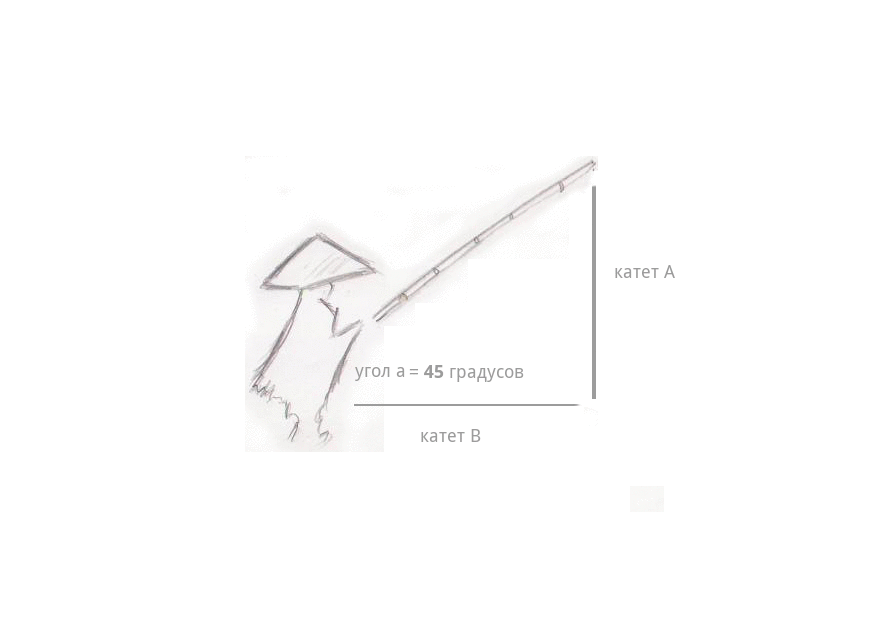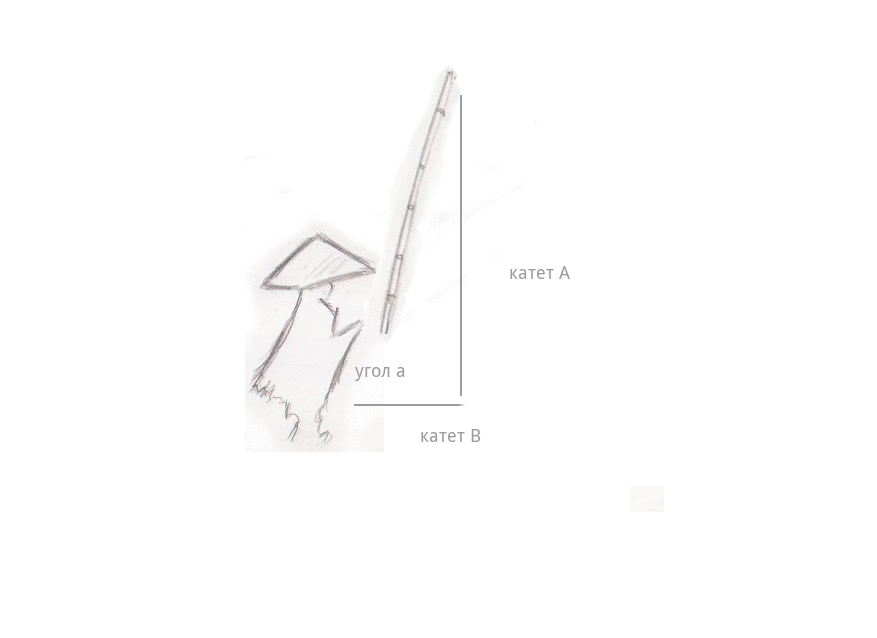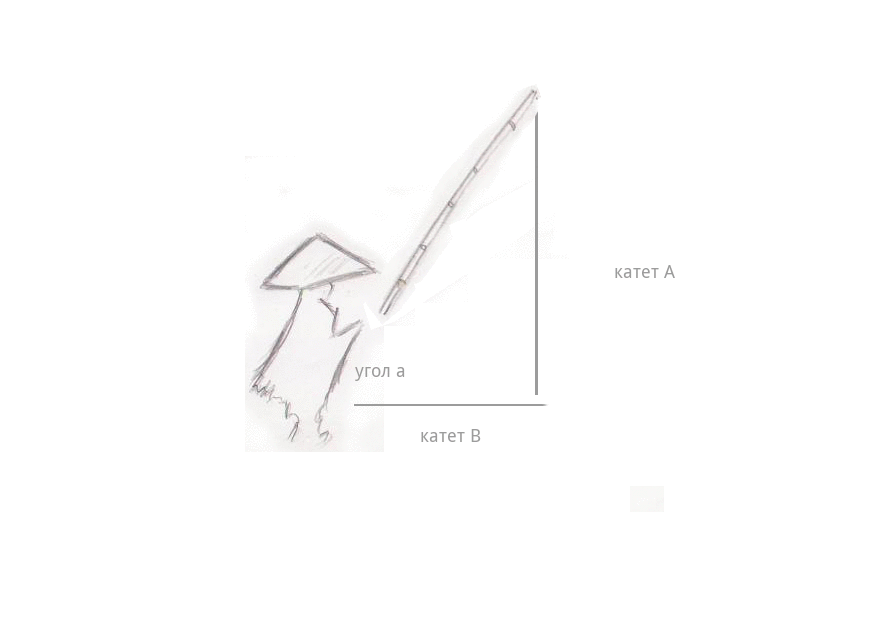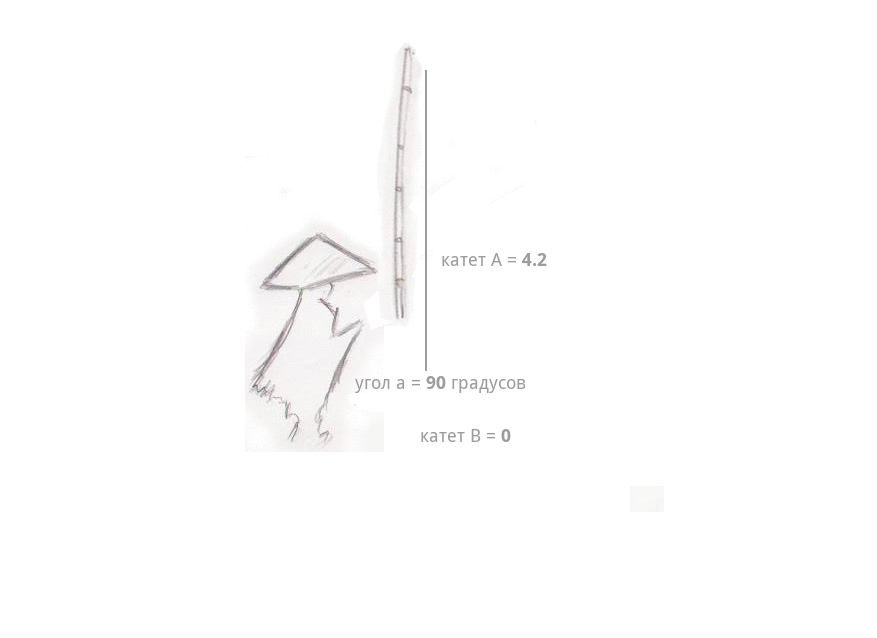
The fisherman’s fishing rod neatly hovered over the surface of the Yellow River at an angle of 45 degrees.
A slight fog spread over the water ... and suddenly - a nod. The fisherman pulled the fishing rod, and it began to quickly gain height, the length of the fishing line (leg A) began to grow before our eyes, and the distance from the fisherman to the fishing line itself began to decrease (leg B). And the most interesting - the length of the fishing rod itself has not changed at all - there were no telescopic fishing rods yet - even when it described an arc in the air and was almost above the head of the fisherman, at an angle of 90degrees. The length of the fishing line was equal to the length of the fishing rod - then there were already reels - and the distance between the fisherman and the fishing line changed to 0 , the fishing line was in the hands of the fisherman.
The last point is very important for understanding what happens when the fishing rod vector is multiplied by the rotation matrix.
Recall the Pythagorean theorem: the square of the length of the fishing rod is the sum of the squares of the legs — the fishing line itself and the distance between the fisherman and the place where the fishing line is immersed in water - C ^ 2 = A squared + B squared.
Imagine that the length of the fishing rod is 4.2 , the length (or height above water) of the fishing line is 3 , the distance between the fisherman and the place where the fishing line is immersed in water is also 3.
1) we find how the length of the fishing line relates to the length of the fishing rod - the sine of the angle a .
2) we will find how the length of the line between the fisherman and the place where the fishing line was dipped corresponds to the length of the fishing rod - cosine a . We consider:
And now let’s speculate.
What happens if the cathetus A is divided by sin (a) ?! those.:
We get the length of the fishing rod - hypotenuse.
And if we multiply the leg A by sin (a) ?!
Note this distance on the hypotenuse - 2.1 .
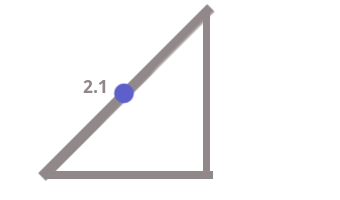
The remaining distance also accounts for - 2.1, since it is obvious:
This means that at the current time, the sine and cosine divide the hypotenuse. Since the square of the hypotenuse is 4.2 * 4.2, the question is: what happens if 4.2 is multiplied by 2.1 ?! On that very part with which one of the legs is connected:
The same for the second leg.
Found the legs. And they were convinced that nothing had changed since the time of Pythagoras.
Now, once again, we multiply the leg of A by sin (a), the leg of B by cos (a).
Summarize:
or
Again we got a number equal to the length of the fishing rod ... and we got close to the rotation matrix.

(Wikipedia image. Link to the article )
Take its lower part - getting the y point :
And compare with the calculations above:
As two drops of water. Y in our case will be equal to 4.2.
If we apply the first part of the formula to the calculations, we get:
In other words, it will happen this way:
x will become 0 - the fisherman will catch the fishing line.
y will become 4.2 - the line will be equal to the length of the fishing rod.
Remember that to calculate x, the sine and cosine are interchanged.
Ф in this case is equal to 45 degrees (Ф = 0.7) and at such an angle the sine and cosine are equal, which is convenient for example. In other cases, obviously, the values for the sine and cosine will be different. For example, for 40 degrees: cosdegree (40) = 0.7660444431, sindegree (40) = 0.6427876097 (if you do not agree, contact Yandex, I used its calculator).
Applying the formula to the new values of x, y several times - in a cycle, we will clearly see the movement in a circle, each time by 45 degrees.
If required to move the bait vector in one degree, and its formula is substituted in the place of F .
How is the calculation of trigonometric functions ?!
As you know, ready-made functions are usually used to calculate the cosine and sine of an angle. According to the link informationcalculation and accuracy are system dependent. For unix systems, there are at least two options: a function written in the bowels of IBM and a built-in fsin instruction in Assembler. There is also a fdlibm library with fairly clear code and comments, which show that the sine and cosine are calculated in this library through the number pi.
If you have a web server and a PHP interpreter on your computer, you can experiment with the following code, which rotates the CSS div block:
If you slightly change the matrix, you can get a rotation in a spiral or make a pendulum from a point.
Bearing in mind that people of different mathematical backgrounds are looking at Habrahabr, however, the topic of linear transformations may well fall into their field of interest, due to its practical significance, I will try to talk about this as much as possible.
Continue the story

The triangular shape of the boat, hats and fishing rods above the water amazed the philosopher and mathematician so much that he froze as if bewitched.
The fisherman’s fishing rod neatly hovered over the surface of the Yellow River at an angle of 45 degrees.
A slight fog spread over the water ... and suddenly - a nod. The fisherman pulled the fishing rod, and it began to quickly gain height, the length of the fishing line (leg A) began to grow before our eyes, and the distance from the fisherman to the fishing line itself began to decrease (leg B). And the most interesting - the length of the fishing rod itself has not changed at all - there were no telescopic fishing rods yet - even when it described an arc in the air and was almost above the head of the fisherman, at an angle of 90degrees. The length of the fishing line was equal to the length of the fishing rod - then there were already reels - and the distance between the fisherman and the fishing line changed to 0 , the fishing line was in the hands of the fisherman.

The last point is very important for understanding what happens when the fishing rod vector is multiplied by the rotation matrix.
We are nostalgic and think further ...
Recall the Pythagorean theorem: the square of the length of the fishing rod is the sum of the squares of the legs — the fishing line itself and the distance between the fisherman and the place where the fishing line is immersed in water - C ^ 2 = A squared + B squared.
Imagine that the length of the fishing rod is 4.2 , the length (or height above water) of the fishing line is 3 , the distance between the fisherman and the place where the fishing line is immersed in water is also 3.
Dive into the search
1) we find how the length of the fishing line relates to the length of the fishing rod - the sine of the angle a .
2) we will find how the length of the line between the fisherman and the place where the fishing line was dipped corresponds to the length of the fishing rod - cosine a . We consider:
sin (a) = 3 / 4.2 = 0.7
cos (a) = 3 / 4.2 = 0.7
And now let’s speculate.
What happens if the cathetus A is divided by sin (a) ?! those.:
3 / 0.7 = 4.2
We get the length of the fishing rod - hypotenuse.
And if we multiply the leg A by sin (a) ?!
3 * 0.7 = 2.1
Note this distance on the hypotenuse - 2.1 .

The remaining distance also accounts for - 2.1, since it is obvious:
4.2-2.1 = 2.1
This means that at the current time, the sine and cosine divide the hypotenuse. Since the square of the hypotenuse is 4.2 * 4.2, the question is: what happens if 4.2 is multiplied by 2.1 ?! On that very part with which one of the legs is connected:
4.2 * 2.1 = 9, (root: 3)
The same for the second leg.
Found the legs. And they were convinced that nothing had changed since the time of Pythagoras.
Further
Now, once again, we multiply the leg of A by sin (a), the leg of B by cos (a).
3 * 0.7 = 2.1
3 * 0.7 = 2.1
Summarize:
2.1 + 2.1 = 4.2
or
3 * 0.7 + 3 * 0.7 = 4.2
Again we got a number equal to the length of the fishing rod ... and we got close to the rotation matrix.
I recall the formula

(Wikipedia image. Link to the article )
Take its lower part - getting the y point :
y = x * sin (Ф) + y * cos (Ф)
And compare with the calculations above:
3 * 0.7 + 3 * 0.7 = 4.2
y = x * sin (Ф) + y * cos (Ф)
As two drops of water. Y in our case will be equal to 4.2.
If we apply the first part of the formula to the calculations, we get:
3 * 0.7 - 3 * 0.7 = 0
In other words, it will happen this way:
x will become 0 - the fisherman will catch the fishing line.
y will become 4.2 - the line will be equal to the length of the fishing rod.
Remember that to calculate x, the sine and cosine are interchanged.
Ф in this case is equal to 45 degrees (Ф = 0.7) and at such an angle the sine and cosine are equal, which is convenient for example. In other cases, obviously, the values for the sine and cosine will be different. For example, for 40 degrees: cosdegree (40) = 0.7660444431, sindegree (40) = 0.6427876097 (if you do not agree, contact Yandex, I used its calculator).
Eventually
Applying the formula to the new values of x, y several times - in a cycle, we will clearly see the movement in a circle, each time by 45 degrees.
If required to move the bait vector in one degree, and its formula is substituted in the place of F .
How is the calculation of trigonometric functions ?!
As you know, ready-made functions are usually used to calculate the cosine and sine of an angle. According to the link informationcalculation and accuracy are system dependent. For unix systems, there are at least two options: a function written in the bowels of IBM and a built-in fsin instruction in Assembler. There is also a fdlibm library with fairly clear code and comments, which show that the sine and cosine are calculated in this library through the number pi.
What if the author of this article came up with everything?
If you have a web server and a PHP interpreter on your computer, you can experiment with the following code, which rotates the CSS div block:
Index.php file
Spoiler heading
< div id="rotation_martix">
If you slightly change the matrix, you can get a rotation in a spiral or make a pendulum from a point.
