November 2, 2017 at 06:32

Reed-Solomon codes. Part 2 - Arithmetic of Galois Fields

    Hello, friends! Last time we started talking about how Reed-Solomon codes help provide the necessary level of data storage reliability. Today we dwell a little more on the arithmetic of the Galois fields, which is used in the calculations. First, a brief excursion into the last part




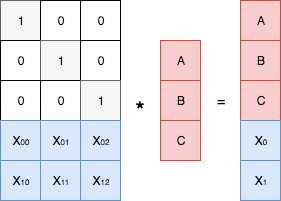
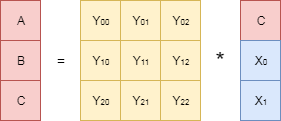
    . We found out - in order to be able to recover lost data, you must first generate “redundant data” in a certain way. Moreover, from a mathematical point of view, this task (coding) is reduced to constructing some generating matrix and performing the operation of multiplying this matrix by a vector of source data. The recovery (decoding) procedure, in turn, consists in reversing the generating matrix and multiplying it by the vector of the saved data. Schematically, this can be represented as follows.

    Encoding



    Procedure: Decoding Procedure:

    image

    Limitations of Arithmetic of Rational Numbers


    We have already noted some difficulties that have to be encountered when implementing encoding / decoding procedures on specific hardware platforms. So, for example, numbers in computer memory are usually represented by a fixed number of bytes. As a result, when multiplying the elements of the generating matrix, one can obtain overflow of bits. Or, when the generating matrix is ​​inverted as its elements, rational numbers can arise that are problematic to store with arbitrary precision. Therefore, today we will talk about how to implement these procedures, avoiding the above problems. The Galois field theory, which we already talked a bit about in a previous article, will help us in this.

    I’ll make a few comments right away. Firstly, the article is primarily intended for an engineering audience, so I tried to avoid rigorous mathematical definitions. For those who want a more formal introduction to this area, it makes sense to immediately turn to the relevant literature. For my part, I can recommend Ernest Borisovich Vinberg's book, A Course in Algebra. Secondly, directly for the implementation of redundant coding algorithms, only a basic understanding of the theory of finite fields is enough. You can simply assume that some consistent tables of multiplication, division, addition, subtraction, and all calculations are performed using these tables. This is a hint for those who do not really want to dive deep into this section of algebra.

    Fields and arithmetic operations in finite sets


    Before proceeding directly to the discussion of the Galois fields, let us repeat once again what we want to achieve. We want to be able to multiply matrices by vectors, invert matrices. And most importantly, we want to deal only with integers and not worry about overflow when performing operations of multiplication and addition.

    Also, to avoid confusion, it makes sense to immediately deal with terminology. First of all, what is a field in terms of general algebra? As Wikipedia tells us, “a field is a set for whose elements the operations of addition, subtraction, multiplication and division (except division by zero) are defined, and the properties of these operations are close to the properties of ordinary numerical operations”. What is the Galois field? Galois Field Is an arbitrary field consisting of a finite number of elements. $ Gf (p) $, $ Gf (p ^ n) $- the standard designation of Galois fields, where the number of field elements is indicated in brackets.

    In modern computers, a fixed number of bits is usually used to store numbers. It’s easy to calculate that everything exists$ 2 ^ n $ different n-bit numbers, from 0 to $ (2 ^ n - 1) $. In other words, we have some finite set of numbers. On this set we will now try in a consistent way to determine the operations of multiplication, division, addition and subtraction. Moreover, so that the result of any operation is also$ n $bit number! In this case, it is said that the set is closed with respect to the introduced operations .

    The subtraction operation in systems of finite sets is usually introduced through the concept of zero and opposite elements. Zero element$ 0 $ Is an element for which equality is true: $ a + 0 = a $where $ a $Is an arbitrary element of the set. Element$ b $is the opposite for$ a $if equality is true $ a + b = 0 $. Usually the opposite element is denoted as$ -a $. If we want from$ x $ subtract $ y $we find the opposite element $ -y $ and stack it with $ x $. Accordingly, in order to be able to subtract arbitrary elements of a finite set, each element of this set must have the opposite.

    The situation is similar with the division operation. The concept of unit and inverse elements is introduced. Single element$ 1 $ Is an element for which equality is true $ a * 1 = a $where $ a $Is an arbitrary element of the set. Element$ b $ (denoted by $ 1 / a $) is called the inverse of $ a $, if $ a * b = 1 $. As with subtraction, if we want$ x $ divide by nonzero $ y $we must find the inverse element $ 1 / y $ and multiply it by $ x $. In order to be able to divide arbitrary elements, each element of the set (except for the zero) must have the opposite.

    Construction of Galois fields GF (p)


    How can we determine the indicated arithmetic operations on a finite set of numbers, so that the set is closed relative to them? In other words, we want to turn an arbitrary finite set of elements into a Galois field. The first thing that comes to mind is to use modular arithmetic. Then if our set contains$ p $ elements, then the result of the product of numbers $ a * b $ will be the number $ (a * b) mod p $. The sum of numbers is defined as$ (a + b) mod p $.

    As an exercise, let's compile addition and multiplication tables for a set consisting of$ p = 5 $ elements $ \ {0, 1, 2, 3, 4 \} $.


    The lower two tables show opposite and opposite values ​​for each element of our set. Armed with these tables, we can perform all the arithmetic operations we need. Hurrah!

    Building Galois Fields $ Gf (p ^ n) $


    We seem to be on the right track to success. The only thing that may not suit us yet is the size of our field - 5. It is clear that to simplify the software implementation, it makes sense to work with sets containing$ 2 ^ n $numbers. Then we can operate with nibbles, bytes, words, etc.

    At first glance it seems to me that the difference is 5 or 256 elements in the set, we take the result of the operation of multiplication or addition by the corresponding module and we are done. Let's try again to make a multiplication table for a set, but this time containing$ 4 = 2 ^ 2 $ element - $ \ {0, 1, 2, 3 \} $. Here's what happened:
    Multiplication table for {0,1,2,3}

    If you look closely at the resulting table, you can find one serious drawback in it. Pay attention to the line for element 2. There is no single element in this line! This means that we will not be able to divide the other elements by 2, since the opposite does not exist for it! This means that it is necessary to construct addition and multiplication tables in some other way. Modular arithmetic, unfortunately, no longer works.

    So, we found out that if the set contains$ 4 = 2 ^ 2 $object, then modular arithmetic does not allow you to specify consistent multiplication operations. In fact, similar problems will arise for any set, the number of elements$ p $which is not a prime number. But what else can you think of?

    Addition to GF (p ^ n)


    Let us assume for simplicity that the set on which we want to define arithmetic operations contains $ 2 ^ n $elements. These are, in fact, numbers$ \ {0, 1, 2, 3, ..., 2 ^ n - 1 \} $. Any number$ a $ from this set can be represented as a decomposition:

    $ a = a_0 + a_12 ^ 1 + a_22 ^ 2 + ... + a_ {n-1} 2 ^ {n-1}, a_i \ in \ {0,1 \} $


    In essence, this is the usual binary representation of a number. Thus, we can also consider any number from our set as a vector of length$ n $whose elements are zeros and ones:

    $ a = [a_0, a_1, a_2, ..., a_ {n-1}], a_i \ in \ {0,1 \} $


    We introduce the operation of adding any two numbers by adding the corresponding binary decomposition vectors. Moreover, the addition of the components of the vectors will be carried out modulo 2 (in the general case, if the number of elements$ p ^ n $modulo $ p $) Thus, the resulting vector will also be a binary representation of a certain number and, as a consequence, will belong to our set (the set will be closed with respect to the addition operation).

    $ a = [a_0, a_1, a_2, ..., a_ {n-1}], a_i \ in \ {0,1 \} \\ b = [b_0, b_1, b_2, ..., b_ {n -1}], b_i \ in \ {0,1 \} \\ c = a + b = [(a_0 + b_0) mod2, ..., (a_ {n-1} + b_ {n-1}) mod2] $


    It is easy to notice that the addition operation we introduced is equivalent to the XOR bitwise operation. Which is very good, since modern processors can perform this operation extremely quickly. But that is not all. It's obvious that$ a \ oplus a = 0 $ for an arbitrary number $ a $. This means that the opposite element to$ a $ is himself $ a $. So in the field$ Gf (2 ^ n) $ addition is the same as subtraction!

    Multiplication in GF (p ^ n)


    It remains to introduce the multiplication operation on our set. This is done as follows. Let's imagine for a while that any number$ a $ from our set is a polynomial of the following form:

    $ a (x) = a_0 + a_1x + a_2x ^ 2 + ... + a_ {n-1} x ^ {n-1}, a_i \ in {0,1} $


    Here the coefficients of the polynomial are taken from the binary expansion of the number $ a $. With this approach, for example, the number$ 100 = 01100100b $ will be mapped to a polynomial $ x ^ 6 + x ^ 5 + x ^ 2 $.

    The operation of multiplication of two numbers we can determine through the multiplication of polynomials corresponding to given numbers:

    $ a × b = (a_0 + a_1x + ... + a_ {n-1} x ^ {n-1}) × (b_0 + b_1x + ... + b_ {n-1} x ^ {n-1}) $


    Moreover, when multiplying, all operations with coefficients of polynomials are performed modulo 2.

    But now, obviously, another problem may arise. When multiplying two polynomials of degree$ n-1 $, we can get a polynomial of a higher degree, which will not correspond to any of the numbers of our set. This is solved as follows. An irreducible polynomial of degree is chosen$ n $. Roughly speaking, this is such a polynomial that cannot be represented as a product of other polynomials, more in the article . After that, using the algorithm for dividing polynomials by a column , which many can still remember from the school curriculum, we divide the result of the product into an irreducible polynomial. I remind you once again that when dividing by a column, operations with coefficients of polynomials are also performed modulo 2. As a result, we obtain a polynomial of degree no higher than$ n-1 $, which we take as the result of the product of two numbers. Here is an example of doing the multiplication of two numbers over a field$ Gf (2 ^ 8) $ using irreducible polynomial $ x ^ 8 + x ^ 4 + x ^ 3 + x + 1 $. This polynomial is used in the AES / Rijndael encryption algorithm.

    We examined the field$ Gf (2 ^ n) $. Custom fields$ Gf (p ^ n) $ are constructed in a similar way, only instead of the binary representation of the number is used $ p $-one and all calculations are carried out modulo $ p $.

    Isomorphism of fields and Galois fields of arbitrary size


    But what happens if we choose another irreducible polynomial? You can even pose a more general question. Suppose I don’t like all these polynomials and column divisions at all, so I’d better come up with my consistent multiplication table using some other principle. Will this be something fundamentally new? The answer is no. All these obtained fields will be isomorphic .

    Translating from the "mathematical" language, isomorphism means that the differences are only in the designation of field elements and one can be reduced to another by choosing the appropriate mapping rule.

    The finite sets of elements that we have examined so far have been of two types. The first type of sets had a number of elements equal to some prime number$ p $. On such sets, we were able to set multiplication and addition tables using only modular arithmetic. The second type includes sets having$ p ^ n $, $ p $ - simple $ n> 1 $number of items. On such sets it is possible to specify multiplication / addition using a scheme with polynomials. Is it possible to set multiplication / addition in a similar way for sets of arbitrary size, say containing 6 elements? The answer is no, it is impossible.

    As a matter of fact, finite fields are called Galois fields, because he discovered their following important properties:

    1. The number of elements of a finite field always has the form $ p ^ n $where $ p $ prime and $ n $ any natural.
    2. All size fields $ p ^ n $ are isomorphic.

    Conclusion


    The second article of the cycle is coming to an end. The first two articles presented brief theoretical information related to Reed-Solomon codes and Galois fields. In the next part I plan to dwell in more detail on the features of the software implementation of the above algorithms. Thanks.
    Tags:

    Also popular now: