The Tale of Resistors and Neon

Calculation of DC circuits on the fingers, or let's read the DAC for ternary logic

But first, neon, what kind of Russian does not like them?

So, again I am with my ternary pieces of iron, but in this article they act as the background, today there is an article about resistors. I sealed several shawls into which gas-discharge lamps of the IN-12 or IN-15 type could be inserted, but I didn’t want to make the clock :)



The simplest shawls carry a pair of sk6812 LEDs to illuminate the cylinder, a dozen transistors and 595e shift registers that control them. This is what a scarf looks like, carrying a single lamp, but at the same time they can be assembled into a long sausage to achieve the desired number of lamps:



Thank you ikaktys for your help! At the same time as the neon women, the ternary counter, which I had previously collected on the breadboard and described in detail, was parted and sealed .



I remind you that my ternary counter uses a balanced ternary number system, which is represented by three voltage levels (-5, 0 and 5 volts). Its status is shown by two-color LEDs: red is a negative value, extinguished is zero, and green is a positive value.

It would seem that this is enough, why are there neon? One friend of mine, who is very sincerely interested in where the ternary path leads me to, turned out to be color blind! So I had to think about an alternative to two-color LEDs. And here the neon box lies, and the decimal display is convenient.

Cross the snake and the hedgehog, or how to make friends binary and ternary logic

Since I, as you know, have an arduino of the brain, I control the neon with the help of the arduino. That is, the neon driver works on binary logic, and I need to output information based on the ternary. I was too lazy to make decryptors, and since I already have arduin, I decided to use the ternary signal to simply add arduins to the ADC, fortunately, it has more than enough free legs. Then we just look in which third of the ADC area the current line is, and this will give us a ternary value inside the arduins.

Only one bad luck: Arduina wants to measure an analog signal between the ground and five volts, and the ternary signal has a spread from minus five to five. By the way, it is sometimes necessary to measure arduino voltage from -5 to 5 V in other areas. For example, recently I needed to measure the current strength in the windings of a DC motor, and the hall sensor gave me exactly a signal from -5 to 5.

That is, I need to scale the voltage level twice and shift it to the positive area. The easiest way to do this is to hang a resistor divider on each ternary line:



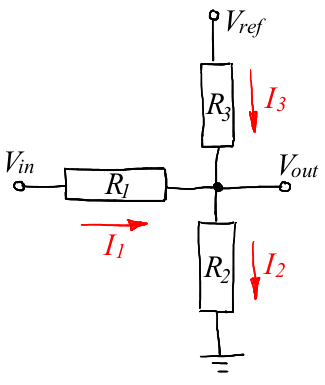
The ternary signal goes into Vin (from -5 to +5 V), the Arduino power is Vref (5 V), and Vout is turned on by the Arduino ADC. This raises the question of how to select the required resistor values ​​so that Vout is in the ADC working area (from 0 to 5 V).

There are probably people who know how to do this almost in their minds, but I don’t belong to them, and I know physics only at the school level. My innermost knowledge is that you do not need to lick the outlet. But I can read, therefore, having read Wikipedia, we arm ourselves with Ohm's law, Kirchhoff's law and the ability to solve linear equations.

To get started, let's set the task like this: knowing the resistances R1, R2 and R3, as well as the voltages Vref and Vin, find the current flowing through each resistor, and at the same time the output voltage Vout.

Let's arbitrarily choose the direction of current flow (indicated by an arrow) through each resistor. If we “made a mistake” with the choice of direction, then simply the current strength will turn out to be negative.

Then we write Kirchhoff’s law for the circuit node (the one that is indicated by the bold black dot in the diagram): the sum of the resulting currents is equal to the sum of the incoming currents, that is, I1 + I3 = I2.

Then the second Kirchhoff rule for a closed loop tells us that the sum of the voltages across the resistors is equal to the total EMF of the loop.

We can choose two circuits, one with a common voltage Vref, the second with a voltage Vin. We write all three equations:



We rewrite the same system in a matrix form, I’m too lazy to solve it with my hands, and in software for symbolic matrix calculations it’s clearly more convenient:



And then the desired currents I1, I2 and I3 can be found by inverting the 3x3 matrix of our system:



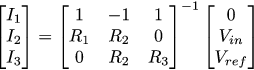
Then the output voltage Vout can be found through the just found I2:



This is fine, but in general our task is not to find Vout by the known resistances and Vin, but vice versa, knowing Vin range, pick up resistance so that Vout fits between zero and Vref.

Let's substitute the 5 volt power supply of the arduins instead of Vref in our equations, we will choose an arbitrary resistor R1 of 100 kOhm (we have a voltage divider, so we can choose one of the resistors ourselves). Then we write two equations: for Vin = -5 Vout should be equal to zero, and for Vin = 5 Vout should be equal to, for example, 4.9 V. That is, we got the following system of equations, I didn’t simplify anything specifically:



In general, a polynomial equation is obtained, it can be counted by hand, but why? I’ll count in sage, here you can execute the code below:

var("R1,R2,R3,Vin,Vout,Vref")
A=matrix([[1,-1,1],[R1,R2,0],[0,R2,R3]])
b=matrix([[0],[Vin],[Vref]])
I=(A.inverse()*b).simplify_full()
I2=I[1][0]
eq1=(4.9==(I2*R2).substitute(Vin= 5,Vref=5,R1=10^5))
eq2=(0  ==(I2*R2).substitute(Vin=-5,Vref=5,R1=10^5))
solve([eq1,eq2],R2,R3)

Here is the output of the solve command:

[[R2 == 0, R3 == 0], [R2 == 2450000, R3 == 100000]]

Our resistors must have strictly positive values ​​of the nominal values, so we will throw away the obviously impossible answers. In total, the solver tells us that if we choose R1 = R3 = 100 kOhm, and R2 = 2.45 megaohm, then when powered by Vref = 5 V, the input voltage range Vin = [- 5 V, + 5 V] will be displayed in the Vout node in range [0 V, 4.9 V]. Hurrah!

Question for attentive readers: why did I choose the output range 0-4.9 V, and not 0-5 V?

Here is the code I'm using:


And here is a video of the work of my ternary counter with a decimal display of the current value on the lamps, three identical divisors wound up on the ADC arduins are clearly visible on it:


I am not very confused by the duality of the display, this does not compromise the work of my ternary calculator, since neon are not a required element, the main output is provided by two-color LEDs.

We complicate the task, go to the DAC

Digital to Analog Binary Conversion

To begin with, let's recall the resistor matrix R-2R for a binary DAC, it looks something like this:



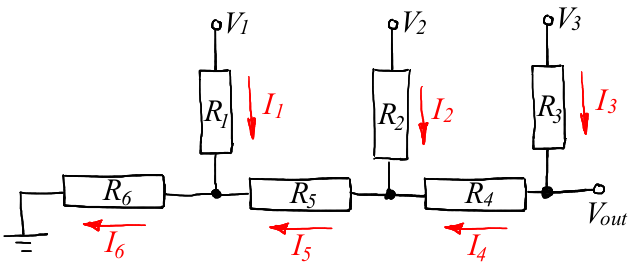
The theory tells us that if we choose R4 = R5 = R, and R1 = R2 = R3 = R6 = 2R, then by applying to the inputs V1, V2, V3 are three bits of a binary number, on the Vout node we get an analog level corresponding to a digital input.

Reading the encyclopedia is good, but how were these R and 2R values ​​obtained? Let's find them ourselves. So, the DAC topology is given to us, as before, we arbitrarily choose the direction of the current flowing through each resistor.

The calculation method for us is exactly the same as in the previous example: first we calculate the current strength at the given resistor values, and then we write a few equations that connect Vout with the inputs V1, V2 and V3, which will give us the desired values.

So, we have three nodes and three circuits, as a result, six equations:



Rewrite in matrix form:



And then the current strength can be found by turning the 6x6 matrix:



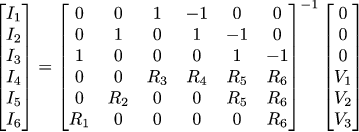
Vout can be obtained as the sum of the voltage drops across three resistors:



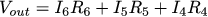
For clarity, let me show you what does Vout look like as a function of R1, R2, R3, R4, R5, R6 and V1, V2, V3:



Quite an unpleasant expression, right? Well, God bless him, we will not count with our hands. So, for given resistor ratings, we have seven non-zero combinations of input voltages on our DAC. They should correspond to seven different values ​​of Vout. This will give seven equations, having solved which, we will get the necessary resistor values.

As before, we will count in sage, here is the code that can be run in the browser .

var("R1,R2,R3,R4,R5,R6,V1,V2,V3")
A=matrix([[0,0,1,-1,0,0],[0,1,0,1,-1,0],[1,0,0,0,1,-1],[0,0,R3,R4,R5,R6],[0,R2,0,0,R5,R6],[R1,0,0,0,0,R6]])
b=matrix([[0],[0],[0],[V3],[V2],[V1]])
I=(A.inverse()*b).simplify_full()
Vo=(I[5][0]*R6+I[4][0]*R5+I[3][0]*R4).simplify_full()
eq7=(7/8==Vo.substitute(V1=1,V2=1,V3=1))
eq6=(6/8==Vo.substitute(V1=0,V2=1,V3=1))
eq5=(5/8==Vo.substitute(V1=1,V2=0,V3=1))
eq4=(4/8==Vo.substitute(V1=0,V2=0,V3=1))
eq3=(3/8==Vo.substitute(V1=1,V2=1,V3=0))
eq2=(2/8==Vo.substitute(V1=0,V2=1,V3=0))
eq1=(1/8==Vo.substitute(V1=1,V2=0,V3=0))
solve([eq1,eq2,eq3,eq4,eq5,eq6,eq7],R2,R3,R4,R5,R6)

Here is the output of the solve command (I threw away all the solutions with negative and zero values ​​of the resistors with my hands):

[R2 == r11, R3 == r12, R4 == -1/2*r11 + r12, R5 == -1/2*R1 + r11, R6 == R1]

This means that we can select the resistors R1, R2, R3 (almost) arbitrarily, and our DAC will work correctly. If we take them all three of the same denomination, then we get the well-known R-2R matrix.

Digital to Analog Ternary Code Conversion

And now we come to the most interesting, to the development of a digital-to-analog converter for a ternary balanced system. As far as I know, no one has done this yet, there are few fools :)

In general, the resistor matrix works great for binary code, but what happens if it receives a ternary signal at its input? If V1 = V2 = V3 = -1, then the output of the matrix will be approximately -1, if V1 = V2 = V3 = 0, then the output is zero, and if V1 = V2 = V3 = 1, then the output is approximately 1. Then There is, in a first approximation, the matrix works as we need. Let's try to fit the resistors so that it works just fine.

The matrix topology remains the same, the expression for Vout does not change, we only need to adjust the system of equations to search for denominations. If earlier we had 7 equations, now it will be 13. Let's try!

var("R,R1,R2,R3,R4,R5,R6,V1,V2,V3")
A=matrix([[0,0,1,-1,0,0],[0,1,0,1,-1,0],[1,0,0,0,1,-1],[0,0,R3,R4,R5,R6],[0,R2,0,0,R5,R6],[R1,0,0,0,0,R6]])
b=matrix([[0],[0],[0],[V3],[V2],[V1]])
I=(A.inverse()*b).simplify_full()
Vo=(I[5][0]*R6+I[4][0]*R5+I[3][0]*R4).simplify_full()
Vo=Vo.substitute(R1==R,R2==R,R3==R)
eq13=(26/27==Vo.substitute(V1= 1,V2= 1,V3= 1))
eq12=(24/27==Vo.substitute(V1= 0,V2= 1,V3= 1))
eq11=(22/27==Vo.substitute(V1=-1,V2= 1,V3= 1))
eq10=(20/27==Vo.substitute(V1= 1,V2= 0,V3= 1))
eq09=(18/27==Vo.substitute(V1= 0,V2= 0,V3= 1))
eq08=(16/27==Vo.substitute(V1=-1,V2= 0,V3= 1))
eq07=(14/27==Vo.substitute(V1= 1,V2=-1,V3= 1))
eq06=(12/27==Vo.substitute(V1= 0,V2=-1,V3= 1))
eq05=(10/27==Vo.substitute(V1=-1,V2=-1,V3= 1))
eq04=( 8/27==Vo.substitute(V1= 1,V2= 1,V3= 0))
eq03=( 6/27==Vo.substitute(V1= 0,V2= 1,V3= 0))
eq02=( 4/27==Vo.substitute(V1=-1,V2= 1,V3= 0))
eq01=( 2/27==Vo.substitute(V1= 1,V2= 0,V3= 0))
sln=solve([eq01,eq02,eq03,eq04,eq05,eq06,eq07,eq08,eq09,eq10,eq11,eq12,eq13],R4,R5,R6)
show(sln)

As usual, this code can be run in a browser.

Well, listen, and the system has a solution, if we take R1 = R2 = R3 = R, R4 = R5 = 4 / 3R and R6 = 2R, then we get a real ternary DAC!

Theory by theory but let's test in practice

In order to check the operation of the DAC, we take the same ternary counter, which I described a little earlier. The counter will be clocked with a triangular saw, the circuit is available here. And we’ll start three categories of our counter on the three inputs of the ternary DAC. This is what the test circuit looks like:



On the breadboard above, the timing triangles, then the counter, on the breadboard below the resistor matrix. There are three resistors in this matrix, I chose 1 kOhm, 1.33 kOhm and 2 kOhm. The three-digit counter counts from -13 to +13, at the output I expect to see a ladder from (approximately) -5 V to (approximately) +5 V. I click on the oscilloscope:



It is perfectly visible that each tacting triangle generates the next step of the ladder to us. Works!

Bonus: how much can you trust math software?

Today we cheerfully considered all kinds of crocodiles software good. In general, how much can you trust what we have calculated? I think a lot of everything, I found bugs in almost all mathematical packages. Here, for example, since we are talking about sage, a screenshot that I took two and a half years ago when I sent a bug report:



Who is right, the numerical integral of the function f or its symbolic calculation? They are even of a different sign! Now the yard is the end of 2017, you can check the current state of things . Versions change, and the error is still in place. Therefore , it is possible to use mathematical software, of course, but you need to check the results in the same way as after the derivation of the formulas on paper .