Data Geometry 5. Basis Transformation
The transformation of the basis of the coordinate system is understood as the replacement of one set of base vertices (frames) with another. Compared with the conventional coordinate system on vectors, a change in the coordinate system on a point basis has features associated with the fact that the bases can belong to different spaces.
In the previous part , we considered the definition of a basis of low dimension in a space of high dimension and showed how to determine the distances between vertices that do not belong to the basis space. When replacing the basis, the requirement to preserve the metric properties of the coordinate system is also key.
Under transformation matrices (transition matrices) is generally understood matrices, which when multiplied by the element coordinates (vertices) in the old basis, its coordinates are obtained by a new one. Based on these matrices, metric tensors are also transformed from one basis to another.
The basis transformation matrices contain comparative characteristics of the two bases. Among these matrices, invariant matrices are distinguished - their values do not depend on the choice of basis. For example, the distance matrix between vertices is invariant.
The set of initial base vertices is denoted as (old basis), new set as
(old basis), new set as  (new basis). To transform the coordinates, a transition matrix must be specified - a description of the coordinates of the vertices of the new basis in the old. Such coordinates can be either the di-coordinates of the vertices or the bi-coordinates. The transition matrix in di-coordinates is denoted as
(new basis). To transform the coordinates, a transition matrix must be specified - a description of the coordinates of the vertices of the new basis in the old. Such coordinates can be either the di-coordinates of the vertices or the bi-coordinates. The transition matrix in di-coordinates is denoted as . The row of the matrix is the coordinates of the top of the new basis
. The row of the matrix is the coordinates of the top of the new basis in the old
in the old  , respectively, the column is the di-coordinates of the top of the old basis relative to the new.
, respectively, the column is the di-coordinates of the top of the old basis relative to the new.
The transition matrix should be square, therefore, the coordinates of the vertices alone are not enough - their number is less than the number of coordinate components (due to the presence of a scalar component in the coordinates). Therefore, it is necessary to add the di-coordinates of the normal vector [0; 1, 1, ... 1]. Then the transition matrix in di-coordinates becomes similar in form to a major gramian. Call the matrix remote coordinate transformation tensor (DTP):
remote coordinate transformation tensor (DTP):

The distance transformation tensor is an invariant — its values are independent of the basis. In the reverse transition (from to
to  ) the values of the given matrix are simply transposed (rows and columns are interchanged).
) the values of the given matrix are simply transposed (rows and columns are interchanged).
Since accidents are di-coordinates, multiplying them by the Laplacian (LMT), we can obtain bi-coordinates . The structure of the bi-coordinates of the transition matrix:
. The structure of the bi-coordinates of the transition matrix:

The first row of this matrix is the bi-coordinates of the normal:![$ [1; 0, 0, ...] $](https://habrastorage.org/getpro/habr/formulas/3f5/c99/032/3f5c99032d536d66bc2c69f79460e0ec.svg) .
.
In contrast to the accident, the values of the bi-coordinates of the transition matrix depend on for what basis they are obtained - for the old or new. The choice of basis determines the LMT matrix. For definiteness, the bi-coordinate of the transition in the basis denote as
denote as  , and in the basis
, and in the basis  as
as  . Then the following identities hold. For the original basis:
. Then the following identities hold. For the original basis:
 ,
, 
and for the new:
 ,
, 
Here and
and  - Laplacian and Gramian of the initial basis. Respectively
- Laplacian and Gramian of the initial basis. Respectively and
and  - metric tensors of a new basis.
- metric tensors of a new basis.
When passing from one basis to another, it is necessary to determine the metric tensors of the new basis if transformation matrices are given.
Transition Matrices and
and  are invertible under the condition that the transition matrix determinant is nonzero:
are invertible under the condition that the transition matrix determinant is nonzero:
 or
or 
The zero determinant of the transformation matrix means the orthogonality of the bases. In the orthogonal basis, it is impossible to express the projection metric. We consider the bases nonorthogonal. Then the inverse transition matrices are expressed through the straight lines as follows:


Matrix - represents the bi-coordinates of the vertices of the old basis
- represents the bi-coordinates of the vertices of the old basis  relative to the peaks of the new
relative to the peaks of the new  . That is, inverting bi-coordinates gives mutual bi-coordinates.
. That is, inverting bi-coordinates gives mutual bi-coordinates.
Matrix Is the Laplace transform of the basis transformation tensor (LTP). Its structure is similar to the structure of the Laplacian (LMT):
Is the Laplace transform of the basis transformation tensor (LTP). Its structure is similar to the structure of the Laplacian (LMT):

Here is the major minor Is a symmetrical Laplacian. In the border, the barycentric coordinates of the back projections of the orthocenters of two bases (simplexes). The orthocenter of the initial basis is expressed in the barycentric coordinates of the new -
Is a symmetrical Laplacian. In the border, the barycentric coordinates of the back projections of the orthocenters of two bases (simplexes). The orthocenter of the initial basis is expressed in the barycentric coordinates of the new - , and the orthocenter of the new in the coordinates of the original -
, and the orthocenter of the new in the coordinates of the original -  .
.
What is meant by “back projections” will be explained below.
In the corner of the Laplace tensor is a scalar . Its value reflects the scalar product of two bases - the new and the old. To reveal its meaning, we consider two situations - 1) the bases belong to the same space and 2) the bases belong to different spaces.
. Its value reflects the scalar product of two bases - the new and the old. To reveal its meaning, we consider two situations - 1) the bases belong to the same space and 2) the bases belong to different spaces.
In general space, the scalar product of bases is expressed in terms of the norms of orthocenters ( and
and  ) and the distance between the orthocenters (
) and the distance between the orthocenters ( ):
):

This formula is similar to the expression for the scalar product of pairs with a common vertex (3.8) . Therefore, we can consider relation (5.5) as the definition of the scalar product of orthocenters.

The figure shows a geometric interpretation of the scalar product of orthocenters (circles). On the left is the definition through the scalar product of adjacent pairs and
and  . If the circles intersect, then they have a common element
. If the circles intersect, then they have a common element - adjacency element of pairs.
- adjacency element of pairs.
The scalar product of elements can be determined through their mutual degrees (shown in the figure to the right). A geometric definition of the degree of a point is given in the 2nd part. According to (2.9), the degree of the point relative to an element is expressed through the distance from the point to the element
relative to an element is expressed through the distance from the point to the element  and the rate of the element
and the rate of the element  :
:

You can generalize this definition if you use another element instead of a point. Then the mutual degree of the two elements and
and  is the following scalar quantity
is the following scalar quantity  :
:

This formula is known as Darboux's product . The right figure shows the construction of points, the distance between which is equal to the mutual degree of the elements:

According to its properties, the mutual degree of the elements generalizes the properties of the degree of a point, that is, determines their relative position. If the elements are outside each other, then their mutual degree is positive; if they intersect, it is negative. By intersection, we mean a situation in which touch points (or
(or  ) are inside the element
) are inside the element  (or
(or  respectively) (in the figure, the mutual degree of the elements is positive).
respectively) (in the figure, the mutual degree of the elements is positive).
Then the scalar product (5.5) is the mutual half-degree of the elements (and vice versa). Recall (2.10) that a semi-degree is a power divided by (-2):

If the centers of the elements coincide ( ), then their scalar product will be equal to their average norm:
), then their scalar product will be equal to their average norm:

If the bases belong to different spaces, then the geometric interpretation of their scalar product complicated. First, we give algebraic identities. They are similar to those for the components of the Laplace tensor given in the first part .
complicated. First, we give algebraic identities. They are similar to those for the components of the Laplace tensor given in the first part .
The scalar product of bases can be expressed in terms of the ratio of the determinants of the distance transition matrix and its main minor (see 5.1.1):

The relationship of the mutual norm of bases and barycentric coordinates of the back projections of their orthocenters:
 - for the vertices of the basis
- for the vertices of the basis  .
.
 - for the vertices of the basis
- for the vertices of the basis  .
.
Let’s figure out what the inverse projection of a point is. Let's say we have a point belonging to the basis
belonging to the basis  . Then its inverse projection onto the basis
. Then its inverse projection onto the basis there will be such a point
there will be such a point  that the perpendicular dropped from it onto the basis
that the perpendicular dropped from it onto the basis  intersects with it at the starting point
intersects with it at the starting point  .
.
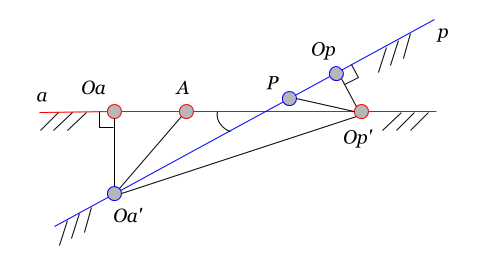
In the figure, the projection of the point to space
to space  is the point
is the point  , and the back projection of the point
, and the back projection of the point  to space
to space  - point
- point  . Points
. Points and
and  Are orthocenters of bases
Are orthocenters of bases  and
and  respectively.
respectively.
The notion of back projection also applies to element norms. The norm in the rear projection becomes larger than the original (in contrast to the direct projection). Distance shown Is the norm of the orthocenter of the basis
Is the norm of the orthocenter of the basis  . Inverse projection onto the basis
. Inverse projection onto the basis there will be a distance:
there will be a distance:
 .
.
Accordingly, the inverse projection of the basis norm
 to basis
to basis  there will be a distance
there will be a distance
 .
.
Denoting the distance between the back projections of the centers as , we obtain the following expression for the scalar product of bases of different spaces:
, we obtain the following expression for the scalar product of bases of different spaces:

We see that in form it coincides with the mutual norm of the bases of one space (5.5), but instead of distances, their inverse projections onto the mutual basis are used. If the bases belong to one space, then the angle between the spaces becomes zero, and formula (5.9) goes over into (5.5).
All the above formulas are also applicable to graph space. There are no described spheres (basis) in the graph, but there is connectivity. Then the scalar product of the bases of the graph should reflect their mutual connectivity.
Here we also consider two situations: 1) the new and old bases belong to the same space and 2) belong to different spaces. The first case, as a rule, refers to ordinary geometric space (when changing the basis, its space rarely changes here), the second refers to the space of the graph.
It is possible to determine whether an element (vertex) belongs to a basis space by its norm in a given space. If equal to zero, then the element belongs to space.
To obtain a new basis gramian it is necessary to multiply the di-coordinates of the elements of the new basis
it is necessary to multiply the di-coordinates of the elements of the new basis  to bi-coordinates
to bi-coordinates  . The resulting matrix will be the matrix of scalar products in the new basis
. The resulting matrix will be the matrix of scalar products in the new basis (see 4.4.2 in the previous part ). Thus, if the basis spaces coincide, then the norm matrix of the vertices of the new basis relative to the old one is the Gramian of the new basis:
(see 4.4.2 in the previous part ). Thus, if the basis spaces coincide, then the norm matrix of the vertices of the new basis relative to the old one is the Gramian of the new basis:

We marked this gramian with a stroke to remember the condition of the general basis space. The Laplacian of the new basis (LMT) can be obtained by reversing the gramian (DMT):

The coordinates of the element in the new basis can be expressed in terms of the coordinates in the old and transition matrices. Di-coordinates :
:

Bi-coordinates of the element in the new basis :
:

All the above expressions are similar to the coordinate change formulas in ordinary (vector) coordinate systems. Within a common space, using a point basis is similar to using a vector basis.
If the bases are in different spaces, then the formula (5.10.1) will give incorrect values of half distances between the vertices of the new basis. In the previous part, it was shown that in the general case, to find the correct distances between the vertices, it is necessary to add a fundamental matrix to the norm matrix (4.5):
(4.5):

Therefore, when transforming a basis to a basis from another space, it is necessary, along with the transition matrices, to specify the fundamental matrix of the new basis (relative to the original).
To define a fundamental matrix, it is useful to recall its geometric meaning (see 4.6.1 ). The element of the fundamental matrix is a scalar product of normals directed to the vertices from their projections onto the basis space. In the particular (but practically important) case of a common superspace, the element of the fundamental matrix is calculated as the product of the distances from the given elements to the basis space.
In the graph space, the values of the fundamental matrix can be obtained through the adjacency matrix between the old and the new basis . The elements of this matrix are the weight of the bonds between the vertices of two bases. If the matrix is known and invertible, then we can obtain the inverse adjacency matrix:
. The elements of this matrix are the weight of the bonds between the vertices of two bases. If the matrix is known and invertible, then we can obtain the inverse adjacency matrix:

The resulting matrix (as well as the adjacency matrix) is an invariant - its values do not depend on the choice of basis. Values of matrix elements reflect the scalar product of the back projections between the vertices of two bases. The figure shows an explanatory diagram.
reflect the scalar product of the back projections between the vertices of two bases. The figure shows an explanatory diagram.
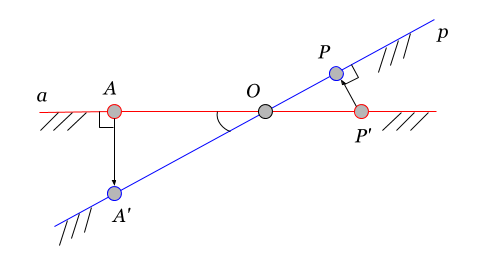
Here point A belongs to the basis , and the point P to the basis
, and the point P to the basis . Dashes indicate the inverse projections of points onto an adjacent basis. Then the value of the matrix element is a scalar product of vectors
. Dashes indicate the inverse projections of points onto an adjacent basis. Then the value of the matrix element is a scalar product of vectors and
and  :
:

This relation can be expressed in terms of the distance from the vertices to the hyperplane of intersection of spaces (in the figure - point O ) and the angle between the spaces :
:

It can be seen from formula (5.13.2 ') that if the bases are orthogonal , then the elements of the scalar product go to infinity.
, then the elements of the scalar product go to infinity.
It is convenient to reduce the dimension of the matrix of scalar products of projections to the dimension of the remaining transition matrices, skirting it with zeros. Then the fundamental matrix of the basis
to the dimension of the remaining transition matrices, skirting it with zeros. Then the fundamental matrix of the basis defined as
defined as

Combining everything together, we obtain the final expression for the Gramian of the new basis :
:

The initial basis is expressed symmetrically for given transformation matrices:

Here and
and  - bi-coordinates of the transition matrices (5.2.1) and (5.2.2).
- bi-coordinates of the transition matrices (5.2.1) and (5.2.2).  - total distance conversion matrix:
- total distance conversion matrix:

This matrix is an invariant, consists of two parts - the remote transformation tensor and additives related to the non-coplanarity of basis spaces - matrixes of scalar products of projections
and additives related to the non-coplanarity of basis spaces - matrixes of scalar products of projections  .
.
The Laplace basis tensor is obtained by the inverse of DMT (5.15). The problem of determining the connection of bases is solved.
To summarize. The heavy formulaic part of the series as a whole is complete. The basic concepts and identities are given. Point bases are a useful and powerful tool for various applications. In the final article, we consider the basis of the simplest structure - in the form of a star.
Table of contents
1. Simplexes and graphs
2. Determination of di- and bi-coordinates
3. Scalar product of pairs
4. Space of a graph
5. Transformation of a basis
6. Star graph
2. Determination of di- and bi-coordinates
3. Scalar product of pairs
4. Space of a graph
5. Transformation of a basis
6. Star graph

In the previous part , we considered the definition of a basis of low dimension in a space of high dimension and showed how to determine the distances between vertices that do not belong to the basis space. When replacing the basis, the requirement to preserve the metric properties of the coordinate system is also key.
Basic matrices
Under transformation matrices (transition matrices) is generally understood matrices, which when multiplied by the element coordinates (vertices) in the old basis, its coordinates are obtained by a new one. Based on these matrices, metric tensors are also transformed from one basis to another.
The basis transformation matrices contain comparative characteristics of the two bases. Among these matrices, invariant matrices are distinguished - their values do not depend on the choice of basis. For example, the distance matrix between vertices is invariant.
Direct transition matrices
The set of initial base vertices is denoted as
The transition matrix should be square, therefore, the coordinates of the vertices alone are not enough - their number is less than the number of coordinate components (due to the presence of a scalar component in the coordinates). Therefore, it is necessary to add the di-coordinates of the normal vector [0; 1, 1, ... 1]. Then the transition matrix in di-coordinates becomes similar in form to a major gramian. Call the matrix
The distance transformation tensor is an invariant — its values are independent of the basis. In the reverse transition (from
Since accidents are di-coordinates, multiplying them by the Laplacian (LMT), we can obtain bi-coordinates
The first row of this matrix is the bi-coordinates of the normal:
In contrast to the accident, the values of the bi-coordinates of the transition matrix depend on for what basis they are obtained - for the old or new. The choice of basis determines the LMT matrix. For definiteness, the bi-coordinate of the transition in the basis
and for the new:
Here
When passing from one basis to another, it is necessary to determine the metric tensors of the new basis if transformation matrices are given.
Inverse transition matrices
Transition Matrices
The zero determinant of the transformation matrix means the orthogonality of the bases. In the orthogonal basis, it is impossible to express the projection metric. We consider the bases nonorthogonal. Then the inverse transition matrices are expressed through the straight lines as follows:
Matrix
Matrix
Here is the major minor
What is meant by “back projections” will be explained below.
In the corner of the Laplace tensor is a scalar
Scalar product of bases of one space
In general space, the scalar product of bases is expressed in terms of the norms of orthocenters (
This formula is similar to the expression for the scalar product of pairs with a common vertex (3.8) . Therefore, we can consider relation (5.5) as the definition of the scalar product of orthocenters.

The figure shows a geometric interpretation of the scalar product of orthocenters (circles). On the left is the definition through the scalar product of adjacent pairs
The scalar product of elements can be determined through their mutual degrees (shown in the figure to the right). A geometric definition of the degree of a point is given in the 2nd part. According to (2.9), the degree of the point
You can generalize this definition if you use another element instead of a point. Then the mutual degree of the two elements
This formula is known as Darboux's product . The right figure shows the construction of points, the distance between which is equal to the mutual degree of the elements:
According to its properties, the mutual degree of the elements generalizes the properties of the degree of a point, that is, determines their relative position. If the elements are outside each other, then their mutual degree is positive; if they intersect, it is negative. By intersection, we mean a situation in which touch points
Then the scalar product (5.5) is the mutual half-degree of the elements (and vice versa). Recall (2.10) that a semi-degree is a power divided by (-2):
If the centers of the elements coincide (
Scalar product of bases of different spaces
If the bases belong to different spaces, then the geometric interpretation of their scalar product
The scalar product of bases can be expressed in terms of the ratio of the determinants of the distance transition matrix and its main minor (see 5.1.1):
The relationship of the mutual norm of bases and barycentric coordinates of the back projections of their orthocenters:
Let’s figure out what the inverse projection of a point is. Let's say we have a point

In the figure, the projection of the point
The notion of back projection also applies to element norms. The norm in the rear projection becomes larger than the original (in contrast to the direct projection). Distance shown
Accordingly, the inverse projection of the basis norm
Denoting the distance between the back projections of the centers as
We see that in form it coincides with the mutual norm of the bases of one space (5.5), but instead of distances, their inverse projections onto the mutual basis are used. If the bases belong to one space, then the angle between the spaces becomes zero, and formula (5.9) goes over into (5.5).
All the above formulas are also applicable to graph space. There are no described spheres (basis) in the graph, but there is connectivity. Then the scalar product of the bases of the graph should reflect their mutual connectivity.
Calculation of a new basis
Here we also consider two situations: 1) the new and old bases belong to the same space and 2) belong to different spaces. The first case, as a rule, refers to ordinary geometric space (when changing the basis, its space rarely changes here), the second refers to the space of the graph.
It is possible to determine whether an element (vertex) belongs to a basis space by its norm in a given space. If equal to zero, then the element belongs to space.
Single basis space
To obtain a new basis gramian
We marked this gramian with a stroke to remember the condition of the general basis space. The Laplacian of the new basis (LMT) can be obtained by reversing the gramian (DMT):
The coordinates of the element in the new basis can be expressed in terms of the coordinates in the old and transition matrices. Di-coordinates
Bi-coordinates of the element in the new basis
All the above expressions are similar to the coordinate change formulas in ordinary (vector) coordinate systems. Within a common space, using a point basis is similar to using a vector basis.
Baseline conversion example
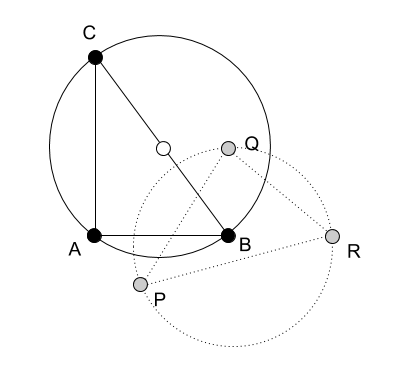
KDPV shows the main basis  из 3-х вершин (A, B, C) и новый базис
из 3-х вершин (A, B, C) и новый базис  , образованный вершинами (P, Q, R). Значения ДМТ основного базиса есть в первой статье:
, образованный вершинами (P, Q, R). Значения ДМТ основного базиса есть в первой статье:
\begin{array}{c | c c c c}
Gm_{aa} & * & A & B & C \\
\hline
* & 0 & 1 & 1 & 1 \\
A & 1 & 0 & -4.5 & -8 \\
B & 1 & -4.5 & 0 & -12.5 \\
C & 1 & -8 & -12.5 & 0 \\
\end{array}
Звездочкой обозначена скалярная компонента. Значение лапласиана (ЛМТ) можно получить обращением грамиана (ДМТ).
Дистанционную матрицу перехода считаем заданной. Ее вид:
\begin{array}{c | c c c c}
Dm_{pa} & * & A & B & C \\
\hline
* & 0 & 1 & 1 & 1 \\
P & 1 & -1.0 & -2.5 & -13.0 \\
Q & 1 & -6.5 & -2.0 & -6.5 \\
R & 1 & -12.5 & -2.0 & -20.5 \\
\end{array}
Значения би-координат матрицы перехода получаем по формуле (5.2.1):
\begin{array}{c | c c c c}
Ba_p{}^a & * & A & B & C \\
\hline
* & 1 & 0 & 0 & 0 \\
P & -1.5 & 0.91(6) & 0.(3) & -0.25 \\
Q & 2.0 & -0.5 & 1.0 & 0.50 \\
R & -5.0 & -0.(6) & 1.(6) & 0.0 \\
\end{array}
Скалярной компонентой (значения первого столбца) би-координат являются орбитали. Сумма барицентрических компонент равна 1.
Лапласовский тензор преобразования (5.3.1):
\begin{array}{c | c c c c}
Lt^{ap} & * & P & Q & R \\
\hline
* & 2.15 & 0.30 & 1.15 & -0.45 \\
A & 0.058(3) & 0.11(6) & -0.0(6) & -0.05 \\
B & 0.9(6) & -0.0(6) & -0.0(3) & 0.10 \\
C & -0.025 & -0.05 & 0.10 & -0.05 \\
\end{array}
Вектор![$ [0.30, 1.15, -0.45] $](https://habrastorage.org/getpro/habr/formulas/9e9/4df/3ac/9e94df3ace26c340fb032a028df423a1.svg) — это барицентрические координаты ортоцентра старого базиса (симплекса ABC) относительно вершин нового (PQR). Соответственно, вектор
— это барицентрические координаты ортоцентра старого базиса (симплекса ABC) относительно вершин нового (PQR). Соответственно, вектор ![$[0.058(3), 0.9(6), -0.025]$](https://habrastorage.org/getpro/habr/formulas/e99/d96/23e/e99d9623e0eec5977437e6f1020e1861.svg) — наоборот, барицентрические координаты ортоцентра симплекса PQR относительно вершин старого базиса.
— наоборот, барицентрические координаты ортоцентра симплекса PQR относительно вершин старого базиса.
Используя (5.10.1), получаем грамиан нового базиса:
\begin{array}{c | c c c c}
Gm'_{pp} & * & P & Q & R \\
\hline
* & 0 & 1 & 1 & 1 \\
P & 1 & 0 & -6.5 & -8.5 \\
Q & 1 & -6.5 & 0 & -4.0 \\
R & 1 & -8.5 & -4.0 & 0 \\
\end{array}
\begin{array}{c | c c c c}
Gm_{aa} & * & A & B & C \\
\hline
* & 0 & 1 & 1 & 1 \\
A & 1 & 0 & -4.5 & -8 \\
B & 1 & -4.5 & 0 & -12.5 \\
C & 1 & -8 & -12.5 & 0 \\
\end{array}
Звездочкой обозначена скалярная компонента. Значение лапласиана (ЛМТ) можно получить обращением грамиана (ДМТ).
Дистанционную матрицу перехода считаем заданной. Ее вид:
\begin{array}{c | c c c c}
Dm_{pa} & * & A & B & C \\
\hline
* & 0 & 1 & 1 & 1 \\
P & 1 & -1.0 & -2.5 & -13.0 \\
Q & 1 & -6.5 & -2.0 & -6.5 \\
R & 1 & -12.5 & -2.0 & -20.5 \\
\end{array}
Значения би-координат матрицы перехода получаем по формуле (5.2.1):
\begin{array}{c | c c c c}
Ba_p{}^a & * & A & B & C \\
\hline
* & 1 & 0 & 0 & 0 \\
P & -1.5 & 0.91(6) & 0.(3) & -0.25 \\
Q & 2.0 & -0.5 & 1.0 & 0.50 \\
R & -5.0 & -0.(6) & 1.(6) & 0.0 \\
\end{array}
Скалярной компонентой (значения первого столбца) би-координат являются орбитали. Сумма барицентрических компонент равна 1.
Лапласовский тензор преобразования (5.3.1):
\begin{array}{c | c c c c}
Lt^{ap} & * & P & Q & R \\
\hline
* & 2.15 & 0.30 & 1.15 & -0.45 \\
A & 0.058(3) & 0.11(6) & -0.0(6) & -0.05 \\
B & 0.9(6) & -0.0(6) & -0.0(3) & 0.10 \\
C & -0.025 & -0.05 & 0.10 & -0.05 \\
\end{array}
Вектор
Используя (5.10.1), получаем грамиан нового базиса:
\begin{array}{c | c c c c}
Gm'_{pp} & * & P & Q & R \\
\hline
* & 0 & 1 & 1 & 1 \\
P & 1 & 0 & -6.5 & -8.5 \\
Q & 1 & -6.5 & 0 & -4.0 \\
R & 1 & -8.5 & -4.0 & 0 \\
\end{array}
Базисы в разных пространствах
If the bases are in different spaces, then the formula (5.10.1) will give incorrect values of half distances between the vertices of the new basis. In the previous part, it was shown that in the general case, to find the correct distances between the vertices, it is necessary to add a fundamental matrix to the norm matrix
Therefore, when transforming a basis to a basis from another space, it is necessary, along with the transition matrices, to specify the fundamental matrix of the new basis (relative to the original).
To define a fundamental matrix, it is useful to recall its geometric meaning (see 4.6.1 ). The element of the fundamental matrix is a scalar product of normals directed to the vertices from their projections onto the basis space. In the particular (but practically important) case of a common superspace, the element of the fundamental matrix is calculated as the product of the distances from the given elements to the basis space.
Scalar Product of Back Projections
In the graph space, the values of the fundamental matrix can be obtained through the adjacency matrix between the old and the new basis
The resulting matrix (as well as the adjacency matrix) is an invariant - its values do not depend on the choice of basis. Values of matrix elements

Here point A belongs to the basis
This relation can be expressed in terms of the distance from the vertices to the hyperplane of intersection of spaces (in the figure - point O ) and the angle between the spaces
It can be seen from formula (5.13.2 ') that if the bases are orthogonal
Final basis transformation formulas
It is convenient to reduce the dimension of the matrix of scalar products of projections
Combining everything together, we obtain the final expression for the Gramian of the new basis
The initial basis is expressed symmetrically for given transformation matrices:
Here
This matrix is an invariant, consists of two parts - the remote transformation tensor
The Laplace basis tensor is obtained by the inverse of DMT (5.15). The problem of determining the connection of bases is solved.
To summarize. The heavy formulaic part of the series as a whole is complete. The basic concepts and identities are given. Point bases are a useful and powerful tool for various applications. In the final article, we consider the basis of the simplest structure - in the form of a star.
