Orientation of a mobile robot, selection of a method for registering particular image points
→ This is the background and continuation of the article:
It was in the evening ...all the articles on Habré were read , a "small" project was launched on the autonomous orientation of the robot on RaspberryPi 3. There is no problem with iron, it is assembled inexpensively from Mr. and sticks of parts purchased for e-bah, camera with good glass optics (this is important for stability of calibrations), a camera drive up, down and a compass, gyroscope, etc. attached to the camera:

Existing SLAM systems do not suit either price or quality / speed. Since I have a lot of details for Visual SLAM, I decided to write and spread the algorithms and code in the public domain step by step, with justification of the reasons for choosing particular algorithms.
In general, the plan is as follows (everything in C ++, except the last):
The selection of special points and their registration is a critical step both in performance and in accuracy. Existing (known to me) algorithms are not suitable (for this platform), or in speed, or in accuracy (precision).
Point matching algorithms have 3 characteristics:
Since the connected points are used in the future to find the transformation matrix using the RANSAC method, the complexity of which is ~ O ((1 / precision) ^ N) where N is the minimum number of pairs of connected points needed to calculate this matrix. If you are looking for a plane (homography matrix) in 3D (projected in 2D), then N = 4, if there is a rigid transformation of 3D points (fundamental matrix), then N = 5-8. That is, if, for example, precision = 0.1 (10%), then to search for homography you will need tens of thousands of expensive samples, and for fundamental millions. Therefore, an algorithm with high precision was developed and tested.
To check the detection and binding algorithms, there is a standard set of images proposed by Mikolajczyk et al. (Included in the distribution of opencv opencv_extra)
In this set of 8 sets of images, each set consists of 6 pictures.
The first picture is reference. The remaining five are distorted, with increasing distortion. Each set is for its type of distortion (rotation, shift, scale, shutter speed, parallax, blur, de-focus, compression artifacts) Here are the results for various algorithms (SIFT, SURF, AKAZE, BRISK, ORB and developed by BOEV (Bigraph Oriented Edge Voting )), the vertical scale - percentages (more is better) and the horizontal number of the picture in the set (more is more difficult). To the right of the algorithm name is the set execution time (detection + decription + matching).
Set bark (scale + rotation) precision:
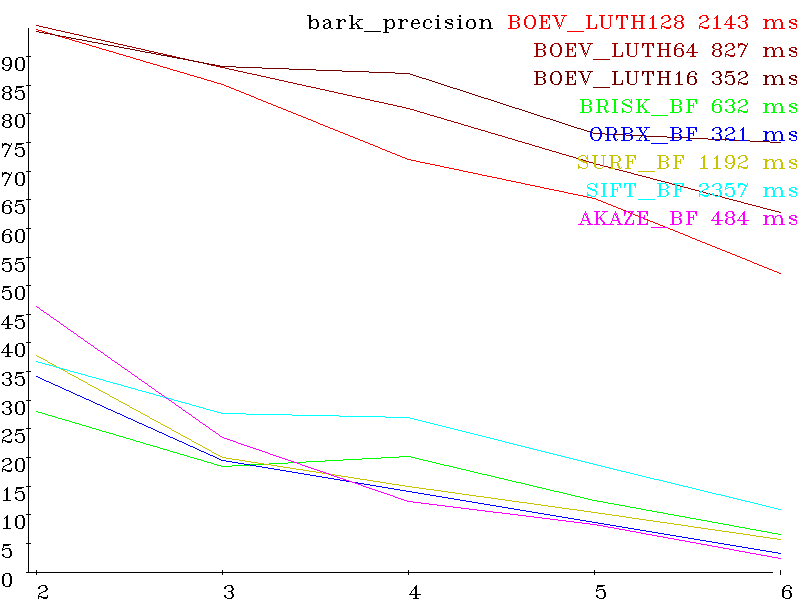
recall:

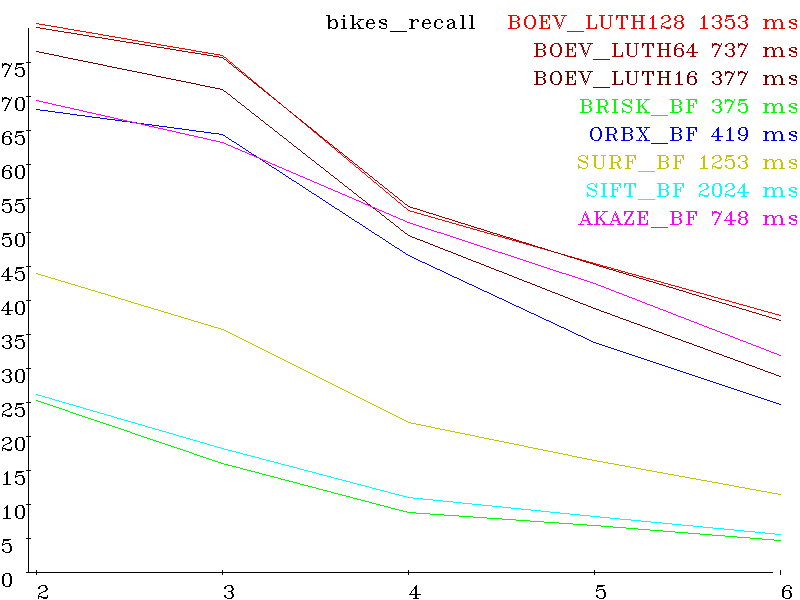
Set bikes (shift + smooth) precision:

recall:
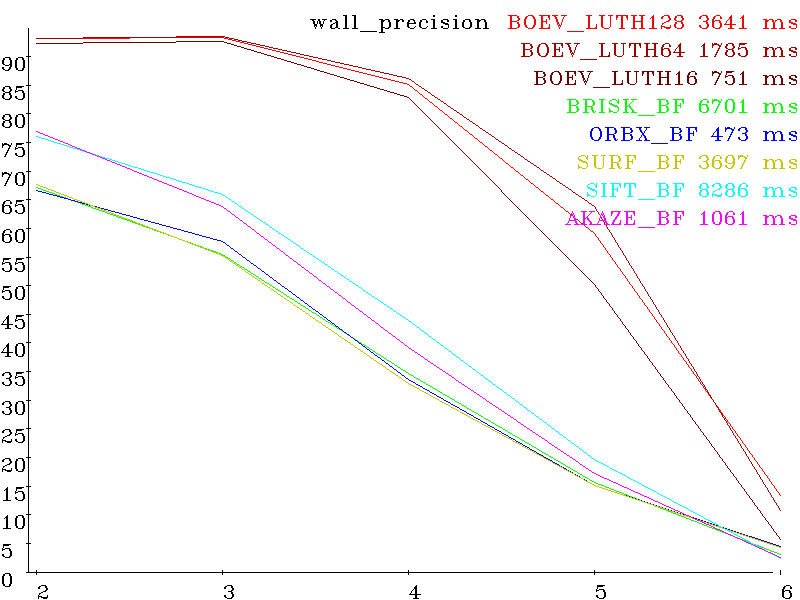
Set wall (perspective distortion) precision:
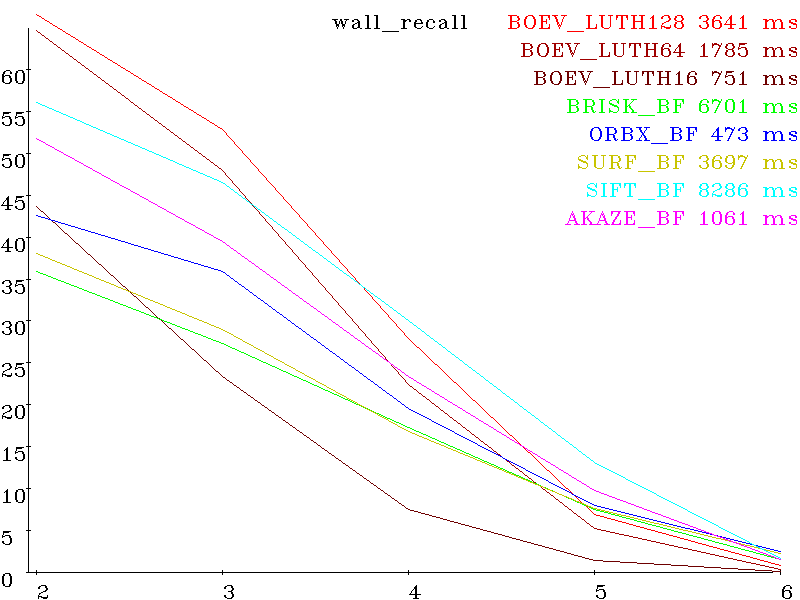
wall recall:
Visible registration results on the example of wall (red - false positive, green true positive)

The rest of the pictures and source code are in the test subdirectory.
This algorithm proved to be very worthy in tests and will be used in the topic of the project.
It was in the evening ...

Existing SLAM systems do not suit either price or quality / speed. Since I have a lot of details for Visual SLAM, I decided to write and spread the algorithms and code in the public domain step by step, with justification of the reasons for choosing particular algorithms.
In general, the plan is as follows (everything in C ++, except the last):
- Capture video from your camera (mainly
skopipastitwritten) - Highlighting special points on each 1 / 1-1 / 8 frame of the image (written)
- Registration of singular points (written)
- Tracing of singular points (easy to write)
- 3D reconstruction of a cloud of points and camera coordinates in it (it is written, not very difficult)
- Drivers for motors, compass, etc. (mostly written
copy-paste) - Writing at least primitive top-level logic, for debugging the previous code (where and why to move, in python, while delayed)
The selection of special points and their registration is a critical step both in performance and in accuracy. Existing (known to me) algorithms are not suitable (for this platform), or in speed, or in accuracy (precision).
Point matching algorithms have 3 characteristics:
- recall (what percentage of points is connected correctly from all detected)
- precision (what percentage of points is connected correctly from all connected)
- speed (detection and binding time)
Since the connected points are used in the future to find the transformation matrix using the RANSAC method, the complexity of which is ~ O ((1 / precision) ^ N) where N is the minimum number of pairs of connected points needed to calculate this matrix. If you are looking for a plane (homography matrix) in 3D (projected in 2D), then N = 4, if there is a rigid transformation of 3D points (fundamental matrix), then N = 5-8. That is, if, for example, precision = 0.1 (10%), then to search for homography you will need tens of thousands of expensive samples, and for fundamental millions. Therefore, an algorithm with high precision was developed and tested.
To check the detection and binding algorithms, there is a standard set of images proposed by Mikolajczyk et al. (Included in the distribution of opencv opencv_extra)
In this set of 8 sets of images, each set consists of 6 pictures.
The first picture is reference. The remaining five are distorted, with increasing distortion. Each set is for its type of distortion (rotation, shift, scale, shutter speed, parallax, blur, de-focus, compression artifacts) Here are the results for various algorithms (SIFT, SURF, AKAZE, BRISK, ORB and developed by BOEV (Bigraph Oriented Edge Voting )), the vertical scale - percentages (more is better) and the horizontal number of the picture in the set (more is more difficult). To the right of the algorithm name is the set execution time (detection + decription + matching).
Set bark (scale + rotation) precision:

recall:

Set bikes (shift + smooth) precision:

recall:

Set wall (perspective distortion) precision:

wall recall:

Visible registration results on the example of wall (red - false positive, green true positive)

The rest of the pictures and source code are in the test subdirectory.
Conclusion
This algorithm proved to be very worthy in tests and will be used in the topic of the project.
