Those familiar with public-key cryptography are probably familiar with the acronyms ECC , ECDH, and ECDSA . The first is an abbreviation for Elliptic Curve Cryptography (cryptography on elliptic curves), the rest are the names of the algorithms based on it.

Today, elliptic curve cryptosystems are used in TLS , PGP and SSH , the most important technologies on which the modern web and IT world are based. I'm not talking about Bitcoin and other cryptocurrencies.

Before ECC became popular, almost all public key algorithms were based on RSA, DSA and DH, alternative cryptosystems based on modular arithmetic. RSA and company are still popular, and are often used with ECC. However, despite the fact that the magic underlying RSA and similar algorithms is easy to explain and understandable to many, and rude implementations are written quite simply , the basics of ECC are still a mystery to most people.

In this series of articles, I will introduce you to the basics of the world of cryptography on elliptic curves. My goal is not to create a complete and detailed guide to ECC (the Internet is full of information on this topic), but a simple overview of ECC and an explanation of why it is considered safe. I will not spend time on long mathematical proofs or boring implementation details. I will also provide useful examples with visual interactive tools and scripts .

In particular, I will consider the following topics:

1. Elliptic curves over real numbers and group law
2. Elliptic curves over finite fields and the discrete logarithm problem
3. Key pair generation and two ECC algorithms: ECDH and ECDSA
4. ECC Hacking Algorithms and Comparison with RSA

To understand the article, you need to know the basics of set theory, geometry and modular arithmetic, understand the principles of symmetric and asymmetric cryptography. Finally, you must clearly understand what the “simple” and “complex” tasks are and their roles in cryptography.

Ready? Let's get started!

Part 1: elliptic curves over real numbers and group law

Elliptical curves

First: what is an elliptic curve? Wolfram MathWorld has an excellent and comprehensive definition . But for us it is enough that an elliptic curve is just a set of points described by the equation :

$$

Where $$, (this is necessary in order to exclude special curves ). The above equation is called the usual Weierstrass formulation for elliptic curves.


Different shapes of elliptic curves ($$, $$ varies from 2 to -3).


Types of features: on the left - a curve with a return point (cusp) ($$) On the right is a self-intersecting curve ($$) Both of these examples are not complete elliptic curves.

Depending on the values$$ and $$elliptic curves can take on a plane different shapes. As you can easily see and check, the elliptic curves are symmetric about the axis$$.

For our purposes, we will also need the infinitely distant point (also known as the ideal point) to be part of the curve . From now on, we will denote an infinitely distant point by the symbol 0 (zero).

If we need to explicitly take into account a point at infinity, then the definition of an elliptic curve can be clarified as follows:

$$

Groups

In mathematics, a group is a set for which we have defined a binary operation called “addition” and denoted by +. To set$$ was a group, addition must be defined in such a way that it corresponds to the following four properties:

1. circuit: if$$ and $$ are included $$then $$ included in $$;
2. associativity:$$;
3. there is a unit element 0 such that$$;
4. each element has an inverse value , that is: for each$$ there is such $$, what $$.

If we add the fifth requirement:

1. commutability:$$,

then the group is called an abelian group .

In the usual addition, the set of integers$$is a group (moreover, it is an Abelian group). Many natural numbers$$however, it is not a group because it does not satisfy the fourth property.

The groups are convenient in that if we prove compliance with all four properties, we automatically get some other properties “to the load”. For example: a single element is unique ; in addition, the reciprocal values ​​are unique , that is: for each$$ there is only one $$such that $$ (and we can write $$ as $$) Directly or indirectly, these and other properties of groups will be very useful to us in the future.

Group law for elliptic curves

We can define a group for elliptic curves. Namely:

• the elements of the group are points of an elliptic curve;
• the unit element is the infinitely distant point 0;
• reciprocal of a point$$ Is a point symmetric about the axis $$;
• addition is defined by the following rule: the sum of three nonzero points$$, $$ and $$lying on one straight line will be equal to $$.

The sum of three points located on one straight line is 0.

It is worth considering that in the last rule we need only three points on one straight line, and the order of these three points is not important. This means that if three points$$, $$ and $$ lie on one straight line then $$. Thus, we intuitively proved that our operator + has the properties of associativity and commutativity: we are in an abelian group .

So far, everything is going fine. But how do we calculate the sum of two arbitrary points?

Geometric addition

Due to the fact that we are in the abelian group, we can write $$ as $$. This equation in this form allows us to derive a geometric way of calculating the sum of two points$$ and $$: if we draw a line through$$ and $$, this line intersects the third point of the curve $$ (this is implied because $$, $$ and $$are on the same line) . If we take the reciprocal of this point$$we will find the amount $$.


Draw a straight line through $$ and $$. The line crosses the third point$$. Symmetric to her point$$ is the result $$.

The geometric method works, but needs improvement. In particular, we need to answer several questions:

• What if $$ or $$? Of course, we cannot draw a straight line (0 is not on the plane$$) But since we defined 0 as a single element,$$ and $$ for any $$ and any $$.
• What if $$? In this case, the line passing through two points is vertical and does not intersect the third point. But if$$ is the inverse of $$then $$ from the definition of the reciprocal.
• What if $$? In this case, an infinite number of lines passes through a point. Here, things get a little more complicated. But imagine that the point$$. What happens if we force$$ strive to $$getting closer to her?
  
  
  
  
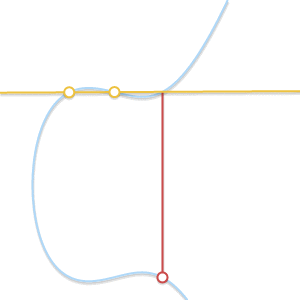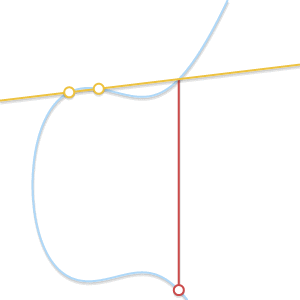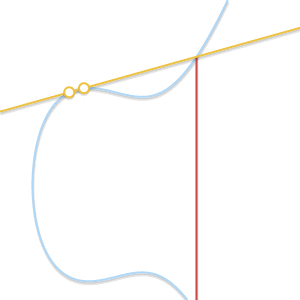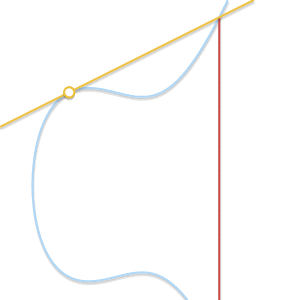
  When two points approach each other, the line passing through them becomes tangent to the curve.
  
  Because the$$ committed to $$straight through $$ and $$becomes tangent to the curve. In light of this, we can say that$$where $$ Is the point of intersection between the curve and the tangent to the curve at $$.
• What if $$but third point $$not? In this case, the situation is similar to the previous one. In fact, in this situation, the line passing through$$ and $$is tangent to the curve.
  
  
  
  
  If our line intersects only two points, then this means that it is tangent to the curve. It is easy to see how the result of addition becomes symmetric to one of the two points.
  
  Let's pretend that$$is a touch point. In the previous case, we recorded$$. This equation now turns into$$. On the other hand, if the point of contact were$$then the equation would be correct $$.

The geometric method is now complete and takes into account all cases. Using a pencil and a ruler, we can add all the points of any elliptic curve. If you want to try it, take a look at the HTML5 / JavaScript visual tool I created to calculate the sums of elliptic curves .

Algebraic addition

If we want the computer to deal with the addition of points, we need to turn the geometric method into an algebraic one. Converting the above rules into a set of equations may seem simple, but in fact it is quite tedious, because it requires solving cubic equations. Therefore, I will only present the results.

To get started, let's get rid of the most annoying deadlocks. We already know that$$, and we know that $$. Therefore, in our equations, we will avoid these two cases and consider only two nonzero asymmetric points$$ and $$.

If$$ and $$do not match ($$), then the straight line passing through them has a slope :

$$

The intersection of this line with the elliptic curve is the third point$$:

$$

or similarly:

$$

therefore $$ (pay attention to the signs and remember that $$)

If we needed to verify the correctness of the result, we would have to check whether$$ curve and whether $$, $$ and $$on one straight line. The verification of being on one straight line is trivial, and the verification of belonging$$curve - no, because we have to solve the cubic equation, which is completely sad.

Instead, let's experiment with an example: according to a visual tool , with$$ and $$belonging to the curve $$, their sum is equal $$. Let's check if this matches the equations:

$$

Yes that's right!

Note that these equations work even when the point$$ or $$is a touch point . Let's check on$$ and $$.

$$

We got the result. $$, which matches the result obtained in the visual tool .

To the occasion$$need to be treated a little differently : equations for$$ and $$ remain the same, but considering that $$we will have to use a different equation for tilting :

$$

Note that, as you might expect, this expression is for $$ is the first derivative:

$$

To prove the correctness of this result, it is enough to verify that $$ belongs to a curve and that line passing through $$ and $$has only two intersections with the curve. But again we will not prove it and instead we will analyze an example:$$.

$$

What gives us $$. Right!

Although the procedure for obtaining the results is very tedious, our equations are quite brief. All this is thanks to the usual formulation of Weierstrass: without it, these equations would be very long and complicated!

Scalar multiplication

In addition to addition, we can define another operation: scalar multiplication , that is:

$$

Where $$- natural number. I also wrote a visual tool for scalar multiplication, so you can experiment with it.

When writing in this form, it’s obvious that the calculation$$ requires $$additions. If$$ comprises $$ decimal places, then the algorithm will have complexity $$which is not very good. But there are faster algorithms.

One of them is the doubling-addition algorithm . The principle of its operation is easier to explain with an example. Take$$. In binary form, it has the form$$. Such a binary form can be represented as the sum of the powers of two:

$$

(We took every binary digit $$and multiplied by the power of two.)

With this in mind, you can write:

$$

The doubling-addition algorithm defines the following procedure:

• To take $$.
• Double it to get$$.
• To fold$$ and $$ (to get the result $$)
• Double$$, To obtain $$.
• Add to the result (to get$$)
• Double$$, receive $$.
• Do not perform addition with $$.
• Double$$, To obtain $$.
• Add to the result (to get$$)
• ...

As a result, we calculate $$by completing a total of seven doublings and four additions.

If this is not completely clear to you, then here is a Python script that implements this algorithm:

def bits(n):
    """
    Генерирует двоичные разряды n, начиная
    с наименее значимого бита.
    bits(151) -> 1, 1, 1, 0, 1, 0, 0, 1
    """
    while n:
        yield n & 1
        n >>= 1
def double_and_add(n, x):
    """
    Возвращает результат n * x, вычисленный
    алгоритмом удвоения-сложения.
    """
    result = 0
    addend = x
    for bit in bits(n):
        if bit == 1:
            result += addend
        addend *= 2
    return result

If doubling and addition are operations $$then this algorithm has complexity$$ (or $$considering the bit length), which is pretty good. And of course, much better than the original algorithm$$!

Logarithm

For given $$ and $$ we have at least one polynomial calculation algorithm $$. But what about the inverse problem? What if we know$$ and $$, and we need to determine $$? This problem is known as the logarithm problem . We use the word “logarithm” instead of the term “division” for consistency with other cryptosystems (in which exponentiation is used instead of multiplication).

I do not know a single “simple” algorithm for solving the logarithm problem, however, experimenting with multiplication , it is easy to detect some patterns. For example, take a curve$$ and point $$. We can immediately make sure that if$$ odd then $$located on a curve in the left half-plane; if$$ even then $$- in the right half-plane. If we experiment more, we may find other patterns that lead us to write an algorithm for efficiently calculating the logarithm of this curve.

But there is a variation of the logarithm problem: the discrete logarithm problem . As we will see in the next part, if we reduce the domain of definition of elliptic curves, scalar multiplication remains “simple”, and the discrete logarithm becomes a “difficult” task . Such duality is a key feature of cryptography on elliptic curves.

In the next part, we examine finite fields and the discrete logarithmization problem , as well as examples and tools for experiments.

Part 2: elliptic curves over finite fields and the discrete logarithm problem

In the previous part, we discussed how elliptic curves over real numbers can be used to define groups. Namely, we determined the rule of addition of points: the sum of three points lying on one straight line is zero ($$) We derived geometric and algebraic methods for calculating the addition of points.

Then we introduced the concept of scalar multiplication ($$) and found a “simple” algorithm for calculating scalar multiplication: doubling-addition.

Now we will limit the elliptic curves to finite fields rather than real numbers, and see what that changes.

Field of integers modulo p

A final field is, first of all, a set of a finite number of elements. An example of a finite field is the set of integers modulo$$where $$- Prime number. In general, this is written as$$, $$ or $$. We will use the last entry.

For fields, there are two double operations: addition (+) and multiplication (·). Both of them are closed, associative and commutative. For both operations there is a unique unit element and for each element there is a unique element of inverse value. And finally, multiplication is distributive with respect to addition:$$.

The set of integers modulo$$ consists of all integers from 0 to $$. Addition and multiplication work as in modular arithmetic . Here are some examples of operations on$$:

• Addition: $$
• Subtraction: $$
• Multiplication: $$
• Additive inversion: $$. Really:$$
• Multiplicative Inversion: $$

If you are unfamiliar with these equations and want to learn the basics of modular arithmetic, take a course at the Khan Academy .

As we have said integers modulo$$Is a field, therefore all of the properties listed above are saved. Please note that the requirement that$$was a prime number, very important! The set of integers modulo 4 is not a field: 2 does not have a multiplicative inversion (i.e., the equation$$ has no decisions).

Modulo p

Soon we will define elliptic curves for $$but first we need to clearly understand that $$ mean over $$. Simply put:$$, or, in plain text, $$ in the numerator and $$ in the denominator is equal to $$ times the reciprocal $$. This does not surprise us, but it gives us a simple way to do the division: find the reciprocal of the number, and then do a simple multiplication .

The inverse number calculation can be "simply" performed using the extended Euclidean algorithm , which in the worst case has complexity$$ (or $$if we consider the bit length).

We will not go into details of the Euclidean extended algorithm, this is not part of the article, but I will present a working implementation in Python:

def extended_euclidean_algorithm(a, b):
    """
    Возвращает кортеж из трёх элементов (gcd, x, y), такой, что
    a * x + b * y == gcd, где gcd - наибольший
    общий делитель a и b.
    В этой функции реализуется расширенный алгоритм
    Евклида и в худшем случае она выполняется O(log b).
    """
    s, old_s = 0, 1
    t, old_t = 1, 0
    r, old_r = b, a
    while r != 0:
        quotient = old_r // r
        old_r, r = r, old_r - quotient * r
        old_s, s = s, old_s - quotient * s
        old_t, t = t, old_t - quotient * t
    return old_r, old_s, old_t
def inverse_of(n, p):
    """
    Возвращает обратную величину
    n по модулю p.
    Эта функция возвращает такое целое число m, при котором
    (n * m) % p == 1.
    """
    gcd, x, y = extended_euclidean_algorithm(n, p)
    assert (n * x + p * y) % p == gcd
    if gcd != 1:
        # Или n равно 0, или p не является простым.
        raise ValueError(
            '{} has no multiplicative inverse '
            'modulo {}'.format(n, p))
    else:
        return x % p

Elliptical curves over $$

Now we have all the necessary elements for restricting elliptic curves to a field $$. The set of points that in the previous part had the following form:

$$

now turn into:

$$

where 0 is still a point at infinity, and $$ and $$ - two integers in $$.


Curve $$ from $$. Note that for each$$there are a maximum of two points. Also notice the symmetry relative to$$.


Curve $$ Is singular and has a triple point in $$. It is not a true elliptic curve.

What used to be a continuous curve has now become a set of individual points on the plane$$. But it can be proved that despite the restriction of the domain of definition, elliptic curves over$$still create an abelian group .

Point addition

Obviously, we need to slightly modify the definition of addition so that it works for $$. For real numbers, we said that the sum of three points on one line is zero ($$) We can keep this definition, but what does it mean to have three points on one straight line above$$?

We can say that three points are on the same line if there is a line connecting them . Of course, straight over$$ differ from the lines above $$. We can say that the line above$$ Is a lot of points $$satisfying the equation $$ (this is the standard equation of the line with the added part "$$").


Add points for a curve $$at $$ and $$. Notice how the line connecting the points$$“Repeats” itself on the plane.

Given that we are still in the group, the addition of points preserves the properties we already know:

• $$ (from the definition of a single element).
• For $$ reciprocal $$Is a point having the same abscissa but the inverse ordinate. Or, if you like,$$. For example, if the curve is over$$ has a point $$then the inverse will be $$.
• Moreover, $$ (from the definition of the reciprocal).

Algebraic Amount

The equations for performing addition of points are exactly the same as in the previous part , except that we need to add at the end of each expression "$$"Therefore, if $$, $$ and $$then $$ can be calculated in the following way:

$$

If $$then the slope $$ takes the form:

$$

Otherwise, if $$, we get:

$$

The equations have not changed, and this is no coincidence: in fact, these equations work on any field, both finite and infinite (with the exception of $$ and $$which are special cases). I feel it needs to be explained. But there is a problem: proof of the group law usually requires complex mathematical concepts. However, I found Stefan Friedl's proof which uses only the simplest concepts. Read it if you are interested in why these equations work (almost) on any field.

Let us return to the curves - we will not determine the geometric method: in fact, problems will arise with it. For example, in the previous part, we said that to calculate$$ we have to take the tangent to the curve in $$. But in the absence of continuity, the word "tangent" loses all meaning. We can find a way around this and other problems, but the purely geometric way will be too complicated and completely impractical.

Instead, you can experiment with an interactive tool I wrote to make point additions .

Group order of an elliptic curve

We said that an elliptic curve defined over a finite field has a finite number of points. We need to answer an important question: how many points are there in it?

First, let's determine that the number of points in a group is called the group order .

Check all possible values ​​for$$ in the range from 0 to $$ will be an impossible way to count points, because it will require $$ steps, and this task is “difficult” if $$Is a large prime.

Fortunately, there is a faster algorithm for calculating order: Schoof's algorithm . I will not go into its details - the main thing is that it is done in polynomial time, and this is what we need.

Scalar Multiplication and Cyclic Subgroups

For real numbers, multiplication can be defined as:

$$

And again, we can use the doubling-addition algorithm to perform multiplication in $$where $$ Is the number of bits $$) I wrote an interactive tool for scalar multiplication .

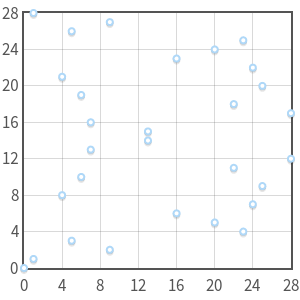
Multiplication of points for elliptic curves over$$has an interesting property. Take a curve$$ and point $$. Now we calculate all values ​​that are multiples of$$:


All values ​​are multiples of $$are five different points ($$, $$, $$, $$, $$) that are cyclically repeated. It is easy to notice the similarity between scalar multiplication for elliptic curves and addition in modular arithmetic.

• $$
• $$
• $$
• $$
• $$
• $$
• $$
• $$
• $$
• $$
• ...

You can immediately notice two features: firstly, values ​​that are multiples of $$, only five: other points of the elliptic curve never become them. Secondly, they are repeated cyclically . You can write:

• $$
• $$
• $$
• $$
• $$

for any whole $$. Note that thanks to the remainder division operator, these five equations can be “squeezed” into one:$$.

Moreover, we can immediately show that these five points are closed with respect to the addition operation . What does it mean: no matter how I summarize$$, $$, $$, $$ or $$, the result will always be one of these five points. And again, all the other points of the elliptic curve never become a result.

The same applies to all other points, not only to$$. In fact, if we take$$ in general:

$$

Which means: if we add two values ​​that are multiples of$$, then we obtain a multiple of $$ (i.e. values ​​that are multiples of $$are closed with respect to the addition operation). This is sufficient to prove that the set of multiple$$values ​​is a cyclic subgroup of a group formed by an elliptic curve.

A “subgroup” is a group that is a subset of another group. A “cyclic subgroup” is a subgroup whose elements are cyclically repeated, as we showed in the previous example. Point$$called a generator or base point of a cyclic subgroup.

Cyclic subgroups are the foundation for ECC and other cryptosystems. Later I will explain why this is so.

Subgroup Order

One may wonder what is the order of the subgroup generated by the point$$ (or, in other words, what is the order $$) We cannot use the Schoof algorithm to answer this question, because this algorithm works only for whole elliptic curves, but not for subgroups. Before proceeding with the solution of the problem, we need some more information:

• So far, we have defined the order as the number of points in the group. This definition is still valid, but in cyclic subgroups we can give a new similar definition: order$$ Is the minimum positive integer $$such that $$.
  
  In fact, if you look at the previous example, then our subgroup consisted of five points, and$$.
• Order $$connected with the order of an elliptic curve by the Lagrange theorem , according to which the order of a subgroup is a divisor of the order of the original group .
  
  In other words, if an elliptic curve contains$$ points, and one of the subgroups contains $$then $$ is a divider $$.

Together, these two facts give us the opportunity to determine the order of the subgroup with the base point. $$:

1. Calculate the order of an elliptic curve $$ using the Schuf algorithm.
2. We find all the dividers $$.
3. For each divisor $$ of order $$ calculate $$.
4. Least $$such that $$, is the order of the subgroup.

For example, a curve $$ over the field $$ has order $$. Its subgroups may be of order$$, $$, $$, $$, $$, $$, $$ or $$. If we substitute$$then we will see that $$, $$, ..., $$that is, order $$ is equal to $$.

Consider that it is important to take the smallest, but not a random divisor . If we choose randomly, we can get$$, which is not the order of the subgroup, but is one of the multiple.

Another example: an elliptic curve defined by the equation$$ over the field $$has order $$which is a prime. Its subgroups can only be ordered$$ or $$. As you can guess when$$, the subgroup contains only an infinitely distant point; when$$, the subgroup contains all points of the elliptic curve.

Base Point Search

ECC algorithms require high-order subgroups. Therefore, an elliptic curve is usually selected, its order is calculated ($$), as the order of the group ($$) a large divisor is selected, and then a suitable base point is found. That is, we do not select a base point, after which we calculate its order, but perform the reverse operation: first we select a fairly good order, and then we look for a suitable base point. How to do this?

First, you need to introduce another concept. The Lagrange theorem implies that the number$$always whole (because$$ - divider $$) Number$$It has its own name: it is a subgroup cofactor .

Now consider that for each point of the elliptic curve there is$$. This is true because$$ Is a multiple of any possible $$. Based on the definition of cofactor, we can write:

$$

Now suppose that $$- prime number (we prefer simple orders for the reasons stated in the first part of the article). This equation, written in this form, tells us that the point$$ creates a subgroup of order $$ (except $$in which the subgroup is of order 1).

In light of this, we can define the following algorithm:

1. Calculate the order $$ elliptic curve.
2. Choose an order $$subgroups. For the algorithm to work, the number must be prime and be a divisor$$.
3. Calculate the cofactor $$.
4. Choose a random point on the curve $$.
5. We calculate $$.
6. If $$ equal to 0, then we return to step 4. Otherwise, we found a subgroup generator with order $$ and cofactor $$.

Note that the algorithm only works if $$simple. If$$ was not easy then order $$ could be one of the dividers $$.

Discrete logarithm

As with continuous elliptic curves, we must now discuss the following question: if we know$$ and $$then what will be $$such that $$?

This task, known as the discrete logarithm problem for elliptic curves, is considered to be “complex” for which no polynomial time algorithm was found running on a classical computer. However, this view does not have mathematical evidence.

This task is similar to the discrete logarithm problem used in other cryptosystems such as Digital Signature Algorithm (DSA), Diffie-Hellman Protocol (DH) and El-Gamal scheme. The names of the tasks do not coincide by chance. Their difference is that these algorithms use not scalar multiplication, but exponentiation modulo. Their discrete logarithm problem can be formulated as follows: if known$$ and $$then what will be $$such that $$?

Both of these problems are “discrete” because they use finite sets (more specifically, cyclic subgroups). And they are “logarithms” because they are similar to ordinary logarithms.

ECC is interesting in that for the moment, the discrete logarithm problem for elliptic curves seems to be “more complicated” compared to other similar tasks used in cryptography. This implies that we need fewer bits for the whole$$in order to get the same level of protection as in other cryptosystems, and we will consider this in detail in the fourth, last, part of the article.

Part 3: ECDH and ECDSA

Scope Parameters

Elliptic curve algorithms will work in a cyclic subgroup of an elliptic curve over a finite field. Therefore, the algorithms will require the following parameters:

• Simple $$defining the size of the final field.
• Odds $$ and $$ elliptic curve equations.
• Base point $$generating a subgroup.
• Order $$ subgroups.
• Cofactor $$ subgroups.

As a result, the parameters of the domain for the algorithms are six$$.

Random curves

When I said that the discrete logarithm problem was “complicated”, I was not entirely accurate. There are certain classes of elliptic curves that are rather weak and allow the use of special algorithms to effectively solve the discrete logarithm problem. For example, all curves for which$$(that is, the order of the final field is equal to the order of the elliptic curve), are vulnerable to Smart attack , which can be used to solve discrete logarithms in polynomial time on classical computers.

Suppose now that I gave you the parameters of the curve definition area. There is a possibility that I discovered a new class of weak curves unknown to anyone, and perhaps I created a “fast” algorithm for computing discrete logarithms for my curve. How can I convince you of the opposite, i.e. that I don’t know about vulnerabilities? How can I guarantee that the curve is “protected” (in the sense that I cannot use it for my own attacks)?

To solve this problem, sometimes you have to use an additional parameter of the definition area:seed value $$. This is a random number used to generate coefficients.$$ and $$ or base point $$or both. These parameters are generated by hash calculation.$$. Hashes, as we know, are “easy” to compute, but “hard” to reverse.


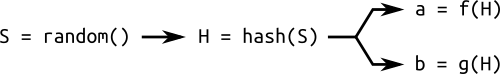
A simple scheme for generating a random curve from a generating value: a random number hash is used to calculate various parameters of the curve.


If we wanted to cheat and recreate the hash from the parameters of the definition domain, then we would have to solve the “difficult” problem: inverting the hash.

The curve generated using the generating value is called checked randomly . The principle of using hashes to generate parameters is known as “ nothing up my sleeve ” and is widely used in cryptography.

This trick gives a certain guarantee that the curve was not specially created in such a way as to have vulnerabilities known to its author . In fact, if I give you a curve along with a generating value, it means that I could not arbitrarily choose the parameters$$ and $$, and you can be relatively calm that I can’t use special attacks. The reason for using the word “relative” will be explained in the fourth part.

A standardized algorithm for generating and checking random curves is described in ANSI X9.62 and is based on SHA-1 . If interested, you can read about the algorithms for generating verifiable random curves in the SECG specification (see "Verifiably Random Curves and Base Point Generators").

I wrote a small Python script that checks all the random curves that ship with OpenSSL right now . I highly recommend watching it!

Elliptic Curve Cryptography

We spent a lot of time, but finally got there! It's simple:

1. The private key is a random integer$$selected from $$ (Where $$ - subgroup order).
2. The public key is the point$$ (Where $$ - base point of the subgroup).

See? If we know$$ and $$ (together with other parameters of the definition domain), then find $$"simply". But if we know$$ and $$then search for the private key$$is a “difficult” problem, because it requires solving the discrete logarithm problem .

We will now describe two public key algorithms based on this principle: ECDH (Elliptic curve Diffie-Hellman, Diffie-Hellman protocol on elliptic curves), used for encryption, and ECDSA (Elliptic Curve Digital Signature Algorithm), used for digital signatures.

Encryption with ECDH

ECDH is a variation of the Diffie-Hellman algorithm for elliptic curves. In fact, it is more likely a key agreement protocol , rather than an encryption algorithm. In essence, this means that ECDH defines (to a certain extent) the order in which keys are generated and exchanged. We can choose the method of encrypting data using such keys ourselves.

It solves the following problem: two parties (usually Alice and Bob ) want to safely exchange information so that a third party ( intermediary, Man In the Middle ) can intercept it, but cannot decrypt it. For example, this is one of the principles of TLS.

Here's how it works:

1. First, Alice and Bob generate their own private and public keys . Alice has a private key$$ and public key $$Bob has the keys $$ and $$. Note that both Alice and Bob use the same definition area parameters: one base point$$ on one elliptic curve in the same finite field.
2. Alice and Bob exchange public keys $$ and $$through an unprotected channel . Intermediary (Man In the Middle) intercepts$$ and $$but cannot identify either $$nor $$without solving the discrete logarithm problem.
3. Alice calculates $$(using Bob’s own private key and Bob’s public key), and Bob calculates$$(using Alice’s own private key and Alice’s public key). Note that$$the same for both Alice and Bob. In fact:
   
   

   $$

However, the intermediary knows only $$ and $$(together with other parameters of the scope) and he will not be able to find a shared secret$$. This is known as the Diffie-Hellman problem, which can be formulated as follows:

What will be the result $$ for three points $$, $$ and $$?

Or similarly:

What will be the result $$ for three whole $$, $$ and $$?

(The latter formulation is used in the original Diffie-Hellman algorithm based on modular arithmetic.)


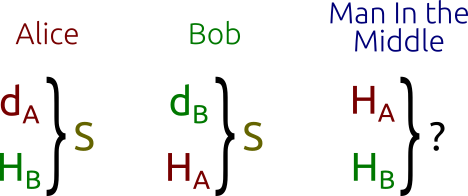
Diffie-Hellman Protocol: Alice and Bob can “simply” calculate the shared secret key, while the intermediary will have to solve the “difficult” problem.

The principle underlying the Diffie-Hellman problem is also explained in the excellent Khan Academy video on YouTube , which later explains the Diffie-Hellman algorithm as applied to modular arithmetic (not elliptic curves).

The Diffie-Hellman problem for elliptic curves is considered "difficult." It is believed that it is as "complicated" as the discrete logarithm problem, but there is no mathematical evidence for this. We can only say with confidence that it cannot be “harder” because solving the logarithm problem is a way to solve the Diffie-Hellman problem.

Having received a shared secret key, Alice and Bob can exchange data with symmetric encryption.

For example, they can use the coordinate$$ the key $$as a key to encrypt messages with secure ciphers like AES or 3DES . That's what TLS does, the difference is that TLS connects the coordinate$$ with other numbers related to the connection, and then calculates the hash of the resulting byte string.

ECDH Experiments

I wrote another Python script to calculate private / public keys and shared secret keys over an elliptic curve .

Unlike the examples shown earlier, this script uses a standardized curve, not a simple curve in a small field. I chose the curve secp256k1of the SECG (Standards for Efficient Cryptography Group, founded by Certicom ). The same curve is used in Bitcoin for digital signatures. Here are the options for the scope:

• $$ = 0xffffffff ffffffff ffffffff ffffffff ffffffff ffffffff fffffffe fffffc2f
• $$ = 0
• $$ = 7
• $$ = 0x79be667e f9dcbbac 55a06295 ce870b07 029bfcdb 2dce28d9 59f2815b 16f81798
• $$ = 0x483ada77 26a3c465 5da4fbfc 0e1108a8 fd17b448 a6855419 9c47d08f fb10d4b8
• $$ = 0xffffffff ffffffff ffffffff fffffffe baaedce6 af48a03b bfd25e8c d0364141
• $$ = 1

(These numbers are taken from the OpenSSL source code .)

Of course, you can change the script and use other curves and parameters of the definition area, just be sure to use simple fields and the usual Weierstrass formulation, otherwise the script will not work.

The script is very simple and contains some of the algorithms described above: point addition, doubling-addition, ECDH. I recommend to study and run it. It creates approximately the following output:

Curve: secp256k1
Alice's private key: 0xe32868331fa8ef0138de0de85478346aec5e3912b6029ae71691c384237a3eeb
Alice's public key: (0x86b1aa5120f079594348c67647679e7ac4c365b2c01330db782b0ba611c1d677, 0x5f4376a23eed633657a90f385ba21068ed7e29859a7fab09e953cc5b3e89beba)
Bob's private key: 0xcef147652aa90162e1fff9cf07f2605ea05529ca215a04350a98ecc24aa34342
Bob's public key: (0x4034127647bb7fdab7f1526c7d10be8b28174e2bba35b06ffd8a26fc2c20134a, 0x9e773199edc1ea792b150270ea3317689286c9fe239dd5b9c5cfd9e81b4b632)
Shared secret: (0x3e2ffbc3aa8a2836c1689e55cd169ba638b58a3a18803fcf7de153525b28c3cd, 0x43ca148c92af58ebdb525542488a4fe6397809200fe8c61b41a105449507083)

Ephemeral ECDH

Some of you may have heard of ECDHE, not ECDH. The “E” in ECHDE stands for “Ephemeral” (ephemeral) and is due to the fact that the keys being transmitted are temporary , not static.

ECDHE is used, for example, in TLS, where the client and server generate their private-public key pair on the fly when establishing a connection. Then the keys are signed with a TLS certificate (for authorization) and transmitted between the parties.

Signing with ECDSA

The scenario is as follows: Alice wants to sign the message with her private key ($$), and Bob wants to verify the signature with Alice’s public key ($$) No one but Alice should be able to create valid signatures. Everyone should be able to verify signatures.

Alice and Bob again use the same scope parameters. We will look at the ECDSA algorithm, a type of Digital Signature Algorithm applied to elliptic curves.

ECDSA works with the message hash, not the message itself. The choice of the hash function remains with us, but, obviously, we need to choose the cryptographic hash function . The message hash must be truncated so that the hash bit length is the same as the bit length$$(subgroup order). A truncated hash is an integer and it will be denoted as$$.

The algorithm performed by Alice to sign the message works as follows:

1. Take a random integer$$selected from $$ (Where $$ - this is still the order of the group).
2. Calculate point $$ (Where $$ - base point of the subgroup).
3. We calculate the number $$ (Where $$ Is the coordinate $$$$)
4. If $$, then choose another $$ and try again.
5. We calculate $$ (Where $$ - Alice’s private key, and $$ - multiplicative inversion $$ modulo $$)
6. If $$, then choose another $$ and try again.

Couple $$is a signature .


Alice signs a hash $$ using private key $$ and random $$. Bob verifies the signature of the message using Alice's public key$$.

Simply put, this algorithm first generates a secret key ($$) Thanks to the multiplication of points (which, as we know, is “simple” in one direction and “complex” in the opposite), the secret key is hidden in$$. Then$$ tied to a message hash by the equation $$.

Note that to calculate$$ we calculated the reciprocal $$ modulo $$. As mentioned in the previous part, this is guaranteed to work only if$$- Prime number. If the subgroup is of a complex order, ECDSA cannot be used. It is no coincidence that all standardized curves have a simple order, and having a difficult order are not applicable to ECDSA.

Signature Verification

To verify the signature, Alice's public key is required $$, (truncated) hash $$ and obviously the signature $$.

1. We calculate the integer $$.
2. We calculate the integer $$.
3. Calculate point $$.

Signature is valid only if $$.

Algorithm correctness

At first glance, the logic of the algorithm may not be obvious, but if we combine all the equations we have written down, everything becomes clearer.

Start with$$. From the definition of the public key, we know that$$ (Where $$- private key). You can write:

$$

Subject to definitions $$ and $$ can be written:

$$

Here we omitted "$$", both for brevity and because the cyclic subgroup generated by the point $$has order $$, that is, the "$$"redundant.

We previously determined$$. Multiplying both sides of the equation by$$ and dividing by $$, we get: $$. Substituting this result in our equation for$$we get:

$$

This is the same equation. $$that we had in step 2 of the signature generation algorithm! When generating signatures and checking them, we calculate the same point$$, just different sets of equations. That is why the algorithm works.

Experimenting with ECDSA

Of course, I wrote a Python script to generate and verify signatures . The code copies some parts from the ECDH script, in particular, the parameters of the definition area and the algorithm for generating the private / public key pair.

Here is the output generated by this script:

Curve: secp256k1
Private key: 0x9f4c9eb899bd86e0e83ecca659602a15b2edb648e2ae4ee4a256b17bb29a1a1e
Public key: (0xabd9791437093d377ca25ea974ddc099eafa3d97c7250d2ea32af6a1556f92a, 0x3fe60f6150b6d87ae8d64b78199b13f26977407c801f233288c97ddc4acca326)
Message: b'Hello!'
Signature: (0xddcb8b5abfe46902f2ac54ab9cd5cf205e359c03fdf66ead1130826f79d45478, 0x551a5b2cd8465db43254df998ba577cb28e1ee73c5530430395e4fba96610151)
Verification: signature matches
Message: b'Hi there!'
Verification: invalid signature
Message: b'Hello!'
Public key: (0xc40572bb38dec72b82b3efb1efc8552588b8774149a32e546fb703021cf3b78a, 0x8c6e5c5a9c1ea4cad778072fe955ed1c6a2a92f516f02cab57e0ba7d0765f8bb)
Verification: invalid signature

As you can see, the script first signs the message (byte string “Hello!”), And then checks the signature. Then he tries to verify the same signature for another message ("Hi there!") And the verification fails. Finally, he tries to verify the verification of the signature for the correct message, but with another random public key, after which verification also fails.

Importance k

When generating ECDSA signatures, it's important to keep secret $$truly secret. If we used one$$for all signatures or a random number generator would be predictable to some extent, the attacker could determine the private key !

Sony made a similar mistake a few years ago. On the PlayStation 3 game console, it was possible to run games only signed by Sony using the ECDSA algorithm. That is, if I wanted to create a new game for the PlayStation 3, I could not distribute it among users without a Sony signature. The problem was that all the signatures created by Sony were generated using static$$.

(It seems that the creators of the random number generator, or inspired by Sony XKCD , or Dilbert .)

In this situation, you can easily recover the private key$$ Sony, having bought only two signed games, then extract their hashes ($$ and $$) and signatures ($$ and $$) together with the parameters of the domain. This is done like this:

• First you need to consider that $$ (because $$ and $$ same for both signatures).
• Accept that $$ (this result follows directly from the equation for $$)
• Multiply both sides of the equation by $$: $$.
• Divided by $$, To obtain $$.

The last equation allows us to calculate $$with just two hashes and their corresponding signatures. Now using the equation for$$ we can get the private key:

$$

Similar techniques can be applied if $$ not static, but somehow predictable.

Part 4: algorithms for hacking ECC protection and comparison with RSA

In the previous part we examined two algorithms (ECDH and ECDSA) and figured out why the discrete logarithm problem for elliptic curves plays an important role for their safety. But, if you remember, we said that there is no mathematical proof of the complexity of the discrete logarithm problem: we believe that it is "complex", but we are not sure about it. In the first part of the article, we tried to evaluate how “difficult” it is in practice in modern technology.

In the second part, we tried to answer the question: why do we need cryptography on elliptic curves if RSA (and other cryptosystems based on modular arithmetic) work well?

Hacking discrete logarithms

Now we will consider two of the most effective algorithms for computing discrete algorithms on an elliptic curve: the baby-step, giant-step algorithm and the Pollard ρ-algorithm.

Before starting, I’ll remind you what the discrete logarithm problem is: find for two given points$$ and $$ integer $$satisfying the equation $$. Points belong to a subgroup of an elliptic curve with a base point$$ and order $$.

Baby-step, giant-step

To begin with, I’ll give a simple argument: we can always write down any whole $$ as $$where $$, $$ and $$- three arbitrary integers. For example, you can write$$.

With this in mind, we can rewrite the equation of the discrete logarithm problem as follows:

$$

Baby-step giant-step is a “meeting in the middle” algorithm. Unlike brute force attack (in which all points have to be calculated$$ for everybody $$until we find $$), it is possible to calculate “several” values ​​for $$ and "several" values ​​for $$until we find a match. The algorithm works as follows:

1. We calculate $$
2. For everybody $$ of $$ calculate $$ and save the results to a hash table.
3. For everybody $$ of $$:
   1. calculate $$;
   2. calculate $$;
   3. check the hash table and look for a point $$such that $$;
   4. if such a point exists, then we found $$.

As you can see, initially we calculate the points $$with a small increment (“baby steps ” ) for the coefficient$$ ($$, $$, $$, ...). In the second part of the algorithm, we calculate the points$$with a large increment ("giant steps" "giant step" ) for$$ ($$, $$, $$, ... where $$ - big number).


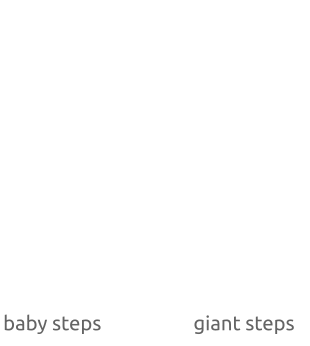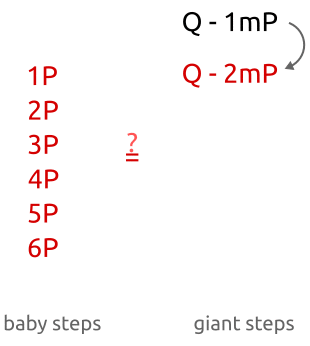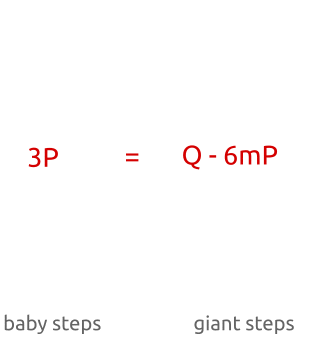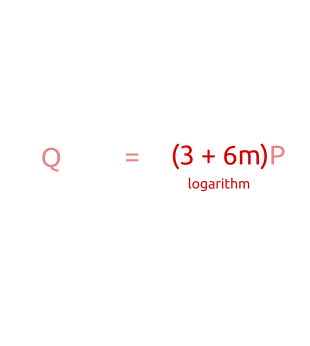
Baby-step, giant-step algorithm: first, we calculate several points with a small step and save them in a hash table. Then we take giant steps and compare the new points with the points in the hash table. Having found a correspondence, we can calculate the discrete algorithm by simple permutation of the terms.

To understand how the algorithm works, forget for a moment that$$ are cached and take the equation $$. Consider what follows from this:

• At $$ we check if $$ the number $$where $$ - one of the integers from 0 to $$. So we compare$$ with all points from $$ before $$.
• At $$ we check whether $$ the number $$. We compare$$ with all points from $$ before $$.
• At $$ we compare $$ with all points from $$ before $$.
• ...
• At $$ we compare $$ with all points from $$ before $$.

As a result, we checked all the points from$$ before $$(that is, all possible points) by completing no more$$additions and multiplications (exactly$$ for "children's steps", no more $$for "giant steps").

Assuming a hash table search takes time$$it’s easy to see that this algorithm has temporal and spatial complexity$$ (or $$if you consider the bit length). This is still an exponential time, but it is much better than with a brute force attack.

Baby-step giant-step in practice

It makes sense to figure out what complexity means. $$on practice. Let's take a standardized curve: prime192v1(she secp192r1, ansiX9p192r1). This curve is of order$$= 0xffffffff ffffffff ffffffff 99def836 146bc9b1 b4d22831. Square root of$$- this is approximately 7.922816251426434 · 10 ²⁸ (almost eighty octillion [approx. Transl.: On a short scale] ).

Imagine what we store$$points in the hash table. Suppose each point occupies exactly 32 bytes: a hash table will require approximately 2.5 · 10 ³⁰ bytes of memory . By searching the Internet , you can find out that the current total capacity of drives around the world has a zettabyte order (10 ²¹ bytes). This is almost ten orders of magnitude less than the amount of memory required by our hash table! Even if the points occupied 1 byte each, we still could not store them all.

This is impressive, and even more impressive, if you remember that prime192v1- this is one of the curves with the smallest order. The order secp521r1(of another standard NIST curve) is approximately 6.9 · 10 ¹⁵⁶ !

Experiments with baby-step giant-step

I wrote a Python script that calculates discrete logarithms using the baby-step giant-step algorithm. Obviously, it only works with small-order curves: do not try to use secp521r1it unless you want to get it MemoryError.

The script produces approximately the following output:

Curve: y^2 = (x^3 + 1x - 1) mod 10177
Curve order: 10331
p = (0x1, 0x1)
q = (0x1a28, 0x8fb)
325 * p = q
log(p, q) = 325
Took 105 steps

ρ Pollard

ρ Pollard is another algorithm for computing discrete logarithms. It has the same asymptotic time complexity.$$as baby-step giant-step, but its spatial complexity is only $$. If baby-step giant-step could not solve the discrete logarithms due to the huge memory requirements, maybe ρ Pollard can handle it? Let's check ...

First, let me remind you again the discrete logarithm problem: find for given$$ and $$ whole $$such that $$. In the Pollard ρ-algorithm, we will solve a slightly different problem: find for given$$ and $$whole $$, $$, $$ and $$such that $$.

Having found four integers, we can use the equation$$ to calculate $$:

$$

Now we can get rid of $$. But before doing this, remember that our subgroup is cyclic and has the order$$, that is, the coefficients used in the multiplication of points are taken modulo $$:

$$

Oll Pollard’s principle of operation is simple: we define a pseudo-random sequence of pairs$$. This sequence of pairs can be used to generate a sequence of points.$$. Because the$$ and $$are elements of one cyclic subgroup, a sequence of points$$also cyclic .

This means that if we go around our pseudo-random sequence of pairs$$then sooner or later we find a cycle. That is: we will find a pair$$ and another separate pair $$such that $$. The same points, separate pairs: we can apply the above equation to find the logarithm.

The challenge is this: how to detect a loop in an efficient way?

Turtle and hare

To detect a loop, we can check all possible values $$ and $$using the pair conversion function , but provided that there is$$ such pairs, the algorithm will have complexity $$, which is much worse than a simple brute force attack.

But there is a faster way: the turtle and hare algorithm (also known as the Floyd cycle finding algorithm). The figure below shows the principle of operation of the tortoise and hare method, on which the Pollard ρ-algorithm is based.


We have a curve $$ and points $$ and $$. The points belong to a cyclic subgroup with order 5. We go around a sequence of pairs with different speeds until we find two different pairs$$ and $$giving one point. In this case, we found pairs$$ and $$, which allows us to calculate the logarithm as $$. And in fact, we did it$$.

In essence, we take a pseudo-random sequence of pairs$$ together with the corresponding sequence of points $$. Sequence of pairs$$ may or may not be cyclic, but the sequence of points is exactly cyclic, because $$ and $$generated from one base point, and from the property of subgroups we know that we cannot “escape” from a subgroup only by scalar multiplication and addition.

Now we take two animals, a turtle and a hare, and make them go around the sequence from left to right. The turtle (the green dot in the image) is slow and reads each dot, one after the other ; The hare (red dot) is fast and skips the dot at every step .

After some time, the turtle and the hare will find one point, but with different pairs of coefficients. Or, to put it in equations, the turtle will find a pair$$and the hare is a couple $$such that $$.

If a random sequence is determined through an algorithm (and not stored statically), it is easy to see that the principle of operation requires everything$$space . Computing the complexity of asymptotic time is not so simple, but we can construct a probabilistic proof showing that the time complexity is$$) , as we have said.

Experimenting with ρ Pollard

I created a Python script that computes discrete logarithms using the Pollard ρ algorithm. This is not an implementation of the original ρ Pollard, but a small variation of it (I used a more efficient way to generate a pseudo-random sequence of pairs). The script has useful comments, so read it if you are interested in the details of the algorithm.

This script, like baby-step giant-step, works for small curves and produces the same output.

Ro Pollard in practice

We said that baby-step giant-step cannot be used in practice due to the huge memory requirements. Pollard's ro-algorithm, on the other hand, requires very little memory. How practical is it?

In 1998, Certicom started the competition for computing discrete logarithms on elliptic curves with a bit length from 109 to 369. To date, only 109 bit curves have been successfully cracked . The last successful attempt was made in 2004. To quote Wikipedia :

The award was presented on April 8, 2004 to approximately 2,600 people represented by Chris Monico. They also used a kind of Pollard’s parallelized ro-algorithm, the calculations on which took 17 months of calendar time.

As we said, prime192v1this is one of the "smallest" elliptic curves. We also said that ρ Pollard has temporary complexity$$. If we used the same technique as Chris Moniko (the same algorithm, the same equipment and the number of machines), how much would it take to calculate the logarithm for prime192v1?

$$

The result obtained speaks for itself and makes it clear how difficult it is to crack a discrete logarithm using such techniques.

Compare ρ Pollard and Baby-step giant-step

I decided to combine the baby-step giant-step script , the Pollard script and the brute force script into a fourth script to compare their performance.

This fourth script calculates all the logarithms for all points on the “small” curve using different algorithms and reports how long it took:

Curve order: 10331
Using bruteforce
Computing all logarithms: 100.00% done
Took 2m 31s (5193 steps on average)
Using babygiantstep
Computing all logarithms: 100.00% done
Took 0m 6s (152 steps on average)
Using pollardsrho
Computing all logarithms: 100.00% done
Took 0m 21s (138 steps on average)

As you might expect, the enumeration method is monstrously slow compared to the other two. Baby-step giant-step is faster, and Pollard's ro-algorithm is more than three times slower than baby-step giant-step (although it uses much less memory and fewer steps on average).

Take a look at the number of steps: on average, 5193 steps were required to calculate each logarithm by brute force. 5193 is very close to 10331/2 (half the order of the curve). Baby-step giant-steps and ro Pollard used 152 steps and 138 steps respectively. These two numbers are very close to the square root of 10331 (101.64).

Further considerations

In the discussion of these algorithms, I used a lot of numbers. When reading them, it is important to be careful: algorithms in many aspects can be greatly optimized. Equipment may be improved. You can create specialized equipment.

If the approach seems impractical today, this does not mean that it cannot be improved. This also does not mean that there are no other, better approaches (do not forget that we have no evidence of the complexity of the discrete logarithm problem).

Shore Algorithm

If modern techniques are not applicable, then what about techniques for the near future? The situation is causing more and more concern: there is already a quantum algorithm capable of computing discrete logarithms in polynomial time: the Shore algorithm with time complexity$$ and spatial complexity $$.

The efficiency of quantum algorithms lies in superposition of the state. On classic computers, memory cells (i.e., bits) can have a value of 1 or 0. There are no intermediate states between them. On the other hand, the memory cells of quantum computers (qubits) are subject to the principle of uncertainty: until they are measured, they do not have a fully defined state. Superposition of the state does not mean that each qubit can simultaneously have the value 0 and 1 (as is often written on the Internet). It means that when measuring a qubit, we have a certain probability of observing 0 and another probability of observing 1. The work of quantum algorithms consists in changing the probability of each qubit.

This oddity means that with a limited number of qubits, we can simultaneously deal with many possible input data at the same time. For example, we can tell a quantum computer that there is a number$$uniformly distributed between 0 and $$. All that is required$$ qubits instead $$bit. Then we can order the quantum computer to perform scalar multiplication$$. As a result, we obtain a superposition of states given by all points from$$ before $$that is, if we now measure all the qubits, we get one of the points from $$ before $$ with probability $$.

I talked about this so that you understand the full power of superposition of states. Shore's algorithm does not work quite like that, in fact it is more complex. It is complicated by the fact that although we can "pretend"$$ states at the same time, at some stage, we will have to reduce this number of states to several, because at the output we need one number, and not several (i.e., we need to know one logarithm, and not a lot of probably erroneous logarithms).

ECC and RSA

Now let's forget about quantum computing, which has not yet become a serious problem. I want to answer the following question: why bother with elliptical curves if RSA already works well?

NIST gave a simple answer by presenting a table comparing the RSA and ECC key sizes needed to get the same level of protection.

RSA key size (bits)	ECC Key Size (bits)
1024	160
2048	224
3072	256
7680	384
15360	521

Note that there is no linear relationship between RSA and ECC key sizes (in other words: if we double the RSA key size, we don’t need to double the ECC key size). The table tells us that ECC not only uses less memory, but generating keys with signing in it is much faster.

But why is this so? The answer is that the fastest algorithms for computing discrete algorithms over elliptic curves are the Pollard ρ-algorithm and baby-step giant-step, and in the case of RSA there are faster algorithms. In particular, one of them is the general method of sieve a number field : an algorithm for factoring integers, which can be used to calculate discrete logarithms. The general method of sieve a number field is by far the fastest algorithm for factoring integers.

All this applies to other cryptosystems based on modular arithmetic, including DSA, Diffie-Hellman and El-Gamal.

Hidden threats of the NSA

Now let's move on to the difficult part. Up to this point, we have discussed algorithms and mathematics. It is time to discuss people, and things are getting more complicated.

If you remember, in the third part we said that some classes of elliptic curves are weak, therefore, to solve the problem of obtaining reliable curves from doubtful sources, we add a random seed value to the parameters of the definition domain. And if you look at the standard NIST curves, you can see that they are verifiable random.

If you read the Wikipedia page about the principle “there is nothing in the sleeves ”, you will notice that:

• Случайные числа для MD5 получаются из синуса целых чисел.
• Случайные числа для Blowfish получаются из первых чисел $$.
• Случайные числа для RC5 получаются из $$ и золотого сечения.

These numbers are random because their numbers are evenly distributed. And they do not raise suspicions, because they have a justification.

Now the following question arises: where do the random generating values ​​for the NIST curves come from? Answer: unfortunately, we do not know. These values ​​have no justification.

Is it possible that NIST discovered a “significantly large” class of weak elliptic curves, tried various possible variants of generating values ​​and found a vulnerable curve? I cannot answer this question, but it is a natural and important question. We know that NIST has at least successfully standardized a vulnerable random number generator(a generator, which, oddly enough, is based on elliptic curves). Perhaps he successfully standardized many weak elliptic curves as well? How to check it? No way.

It is important to understand that “verifiable random” and “protected” are not synonyms. And it doesn’t matter how complicated the logarithm task is or how long the keys are - if the algorithms are cracked, then we can do nothing.

In this regard, the RSA wins because it does not require special domain parameters that can be exploited. RSA (like other modular arithmetic systems) can be a good alternative if we cannot trust the authorities and if we cannot create our own parameters for the definition domain. And if you're curious: yes, TLS can use NIST curves. If you check in google, you will see that when connecting, ECDHE and ECDSA are used with a certificate based on prime256v1(it is secp256p1).

That's all!

I hope you enjoyed this article. I tried to introduce you to the basic information, terminology and assumptions necessary to understand the current state of cryptography on elliptic curves. If I succeeded, then now you can deal with existing ECC-based cryptosystems and expand your knowledge by reading deeper documentation. When writing an article, I skipped a lot of details and used simplified terminology, but I felt that otherwise you would not have understood the information presented on the Internet. I believe that I managed to find a good compromise between the simplicity and completeness of the information.

However, it is worth noting that after reading only this article, you will not be able to implement secure cryptosystems based on ECC: security requires knowledge of many subtle but important details. Remember the requirements for Smart attack and the Sony error - these are two examples of how you can create unsafe algorithms and how easy they can be exploited.

So, if you are interested in diving deeper into the ECC world, then where do you start?

First, while we saw the Weierstrass curves over simple fields, but you should know that there are other types of curves and fields, namely:

• Koblitz curves over binary fields. These are elliptical shaped curves$$ (Where $$ - 0 or 1) over finite fields containing $$ elements (where $$ — простое число). Они обеспечивают особо эффективное сложение точек и скалярное умножение.
  
  Примерами стандартизированных кривых Коблица являются nistk163, nistk283 и nistk571 (три кривые, определённые над полем из 163, 283 и 571 бит).
• Двоичные кривые. Они очень похожи на кривые Коблица и имеют форму $$ (где $$ — целое число, часто генерируемое из случайного порождающего значения). Как подсказывает название, двоичные кривые ограничены только двоичными полями. Примерами стандартизированных кривых являются nistb163, nistb283 и nistb571.
  
  Надо сказать, что возникает всё больше подозрений в том, что кривые Коблица и двоичные кривые могут быть не так безопасны, как простые кривые.
• Кривые Эдвардса имеют вид $$ (где $$ — это 0 или 1). Они особенно интересны не только потому, что для них быстро выполняются сложение точек и скалярное умножение, но и потому, что формула сложения точек всегда одинакова, в любом случае ($$, $$, $$, ...). Эта особенность снижает возможность атак по сторонним каналам (side-channel attack), при которых атакующий измеряет время, использованное для скалярного умножения, и пытается подобрать скалярный коэффициент на основании времени для его вычисления.
  
  Кривые Эдвардса относительно новы (впервые они были представлены в 2007 году), поэтому ни один орган, такой как Certicom или NIST, пока не стандартизировал ни одну из них.
• Curve25519 and Ed25519 are two special elliptical curves created for ECDH and the ECDSA variant respectively. Like the Edwards curves, these two curves are quick and help defend against attacks on third-party channels. Like Edwards curves, these two curves have not yet been standardized and are not used in popular software (with the exception of OpenSSH, which has supported Ed25519 key pairs since 2014).

If you are interested in the details of ECC implementation, I suggest you read the sources of OpenSSL and GnuTLS .

And finally, if you are interested in the mathematical details, and not the safety and efficiency of the algorithms, then you need to know the following:

• Elliptic curves are algebraic varieties of genus 1 .
• Infinitely distant points are studied in projective geometry . They can be represented using uniform coordinates (although most of the properties of projective geometry are not needed for cryptography on elliptic curves).

And don't forget to study finite fields along with field theory .

If you are interested in this topic, then it is worth looking for such keywords.

This article officially ends. Thank you for all the friendly comments, tweets and letters. Many asked if I would write other articles on related topics. My answer is: maybe. You can send your suggestions, but I do not promise anything.